はじめに
近年、構造最適化手法の一種であるトポロジー最適化が実際の製品にも適用され始め、その応用分野は弾性体、振動、伝熱、熱流体など多岐に渡ります。
トポロジー最適化手法は、これまでの歴史の中で様々な手法が提案されてきました[1-5]。トポロジー最適化を実問題に適用する際には、製品の製造方法や扱う物理現象、目的に応じて手法を選択する必要があり、各手法への理解を深めることが重要です。
本記事では、代表的な手法である密度法、均質化法、レベルセット法、そしてここ数年盛んに研究が行われているMoving Morphable Components(MMC)の概要や特徴を紹介します。特に、MMCの解説記事は少ないため、数式表現に踏み込んで説明したいと思います。そして、密度法とMMCをMATLABで実装し、結果の違いを見ていきたいと思います。
感度解析
数理最適化には、目的関数の設計変数に関する感度(勾配)を用いる勾配法、生物の進化を模倣した進化的手法、ランダムに設計空間を探索する総当たり的手法、目的関数の形や勾配などを用いずに入力値と出力値のみから最適解を見つけるブラックボックス最適化など様々な手法が存在します。
本記事では、実装の容易さと探索効率の良さから勾配法を用います。
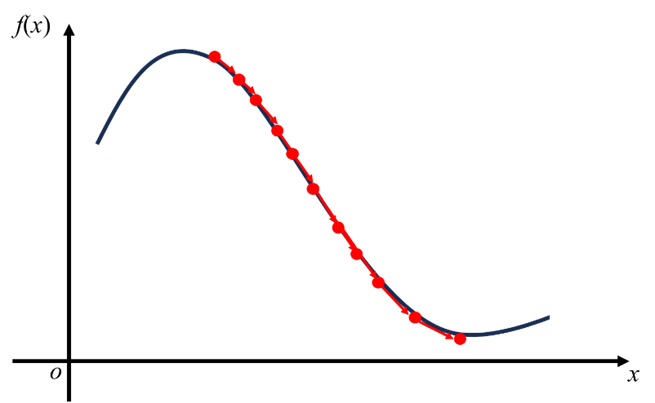
勾配法は、周囲が霧で見渡せない山の斜面での下山によく例えられます。現時点の設計変数xにおける目的関数f(x)の値と勾配\frac{df}{dx}の情報のみから、少しずつ目的関数が小さい方向へ移動することで最小値を目指します。
感度解析とは、目的関数の設計変数に関する感度(勾配)を算出し、目的関数が減少(または増加)するための設計変数を動かすべき方向を解析することを意味します。
目的関数が設計変数で陽に記述されていれば直接微分により感度を算出できますが、そうでない場合は設計変数に微小値を与えて近似的に微分値を計算します。これを数値微分と呼びます。
\frac{df(x)}{dx}
≃\frac{f(x+dx)-f(x-dx)}{2dx}
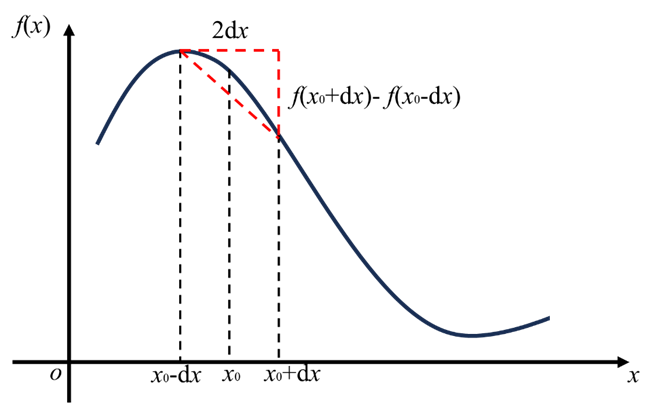
後ほど実装するプログラムにおいて、密度法は目的関数が設計変数で陽に表されているため直接微分をし、MMCは目的関数が設計変数で陽に表されていないため数値微分を用います。
数値微分は目的関数によらず感度を算出できるという利点がありますが、目的関数を複数回評価する必要があるため計算コストを増大させてしまうという欠点があります。
代表的なトポロジー最適化手法の概要
均質化法に基づくトポロジー最適化
均質化法に基づくトポロジー最適化は、マイクロストラクチャと呼ばれる周期的に並ぶミクロ構造を設計領域内に定義し、そのミクロ構造を制御するパラメタを設計変数としてマクロな構造特性を最適化するというコンセプトの手法です。

解析する際には、均質化を行い、マクロ的な力学特性が実際にマイクロストラクチャを有する構造と整合するように定式化します。
手法が提案された当時、マイクロストラクチャを製造することは困難でしたが、近年はAdditive Manufacturingの発展により、様々な材料でマイクロストラクチャの製造が可能となりました。
弊社で均質化法によるトポロジー最適化を行ったラティス構造の試作モデルを掲載します。

マイクロストラクチャの疎密により幾何形状を表現できていることがわかります。このように均質化法に基づくトポロジー最適化は、微細構造を用いて構造部材を最適化したい場合に用いる手法です。
均質化についてより詳しく知りたい方は、過去の技術記事をご一読ください。
(2)アディダス3DPシューズ解説:圧縮力をせん断変形に変換するメカニカルメタマテリアルの設計
メタマテリアルを均質化してみた
(1)ラティス構造の均質化
(2)ラティス構造の均質化
密度法
密度法は、解析に用いる各有限要素に0〜1の規格化された材料濃度を設計変数として与え、その濃度の濃淡を最適化するというコンセプトの手法です。

最適化の枠組みの中で中間濃度にペナルティを与え、なるべく濃度が0と1に二分化されるように工夫します。それでも境界部等でどうしても中間濃度が発生してしまうため、最終的には閾値を設けて材料の有無を決定します。比較的自由度の高い複雑な幾何形状を表現できることが特徴で、多くの汎用CAEソフトウェアに実装されています。
一方、有限要素をピクセルとしたドット絵で幾何形状を表現することに等しく、滑らかな幾何形状を得るには多くの有限要素数を必要とするため、計算コストが増大してしまいます。
また、過度に複雑な幾何形状が創出されてしまう可能性があり、製造方法に合わせて幾何形状をデフォルメすることが必要となる場合もあります。一見、構造の意味することがわからない局所解に収束してしまうこともしばしばあり、創出される幾何形状の示唆することを読み取り、初期値を変えながら最適解を見つけなければならない場合もあります。
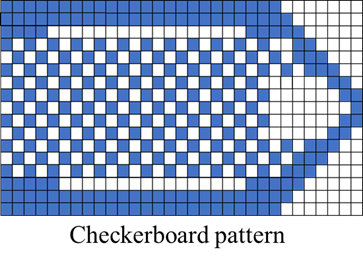
さらに、材料の有無が交互に並んでしまうチェッカーボード現象が問題の1つとして知られています。製造が困難かつ実際に製造したら格子が連結されている角部で壊れてしまいそうですが、数値解析上では剛性が高く評価されるため創出されてしまいます。対応策として、感度や密度にフィルターをかける方法が挙げられます。
レベルセット法に基づくトポロジー最適化
レベルセット法に基づくトポロジー最適化は、設計領域内に分布するレベルセット関数と呼ばれるスカラ関数を設計変数とし、レベルセット関数のゼロ等位面を材料の境界と定義し、少しずつ発展させることによって幾何形状を創出するというコンセプトの手法です。
境界の発展は、疑似的な時間を導入し、目的関数に関する感度を駆動力とすることで達成しています。
密度法のように有限要素単位のドット絵で幾何形状を表現するような手法ではなく、自由形状な境界を持つ幾何形状を明瞭に表現できることが特徴です。
実装上は、設計領域全体の有限要素節点におけるレベルセット関数値のゼロ等位面を更新することとなるため、節点の数に比例して設計変数の数が増加してしまいます。
上記3手法の理論やその応用については,文献[6,7]を始め、数多くのウェブページでも詳説されておりますのでご参照ください。
Moving Morphable Components(MMC)
Moving Morphable Components(MMC)は、解析に用いる有限要素とは別に、あらかじめ最適幾何形状の部材となり得る要素を「構成要素」として設計領域に配置しておき、構成要素の移動、回転、拡大、縮小、重ね合わせで幾何形状を表現するというコンセプトの手法です。

事前に配置する構成要素数は任意に決められるため、製造方法や設計制約に応じて創出される幾何形状の複雑さを制御することが可能です。
幾何形状の表現と解析に用いる有限要素が独立しており、密度法と比べて荒いメッシュ数でも明瞭に幾何形状を表現できます。設計変数の数は構成要素の数のみに依存しているため、有限要素の数を増やしても設計変数の数には無関係です。
加えて、構成要素の寸法を設計変数としているため、部材の寸法を最適化の枠組みの中で直接制御できるのも特徴の1つです。製造上の理由等で最大最小としたい部材寸法が決まっている場合に有用です。
一方、初期値が収束解に影響を与えてしまうため、注意して決定する必要があります。設計変数は、構成要素の中心座標、縦横寸法、回転角度の5つで,それらの初期値を調整しながら最適化を行わなければなりません。
さらに、形状の決まった構成要素の集合体で幾何形状を表現するため、伝熱問題や流路問題など複雑かつ滑らかな形状を表現すべき問題には不向きだと言えるでしょう。しかし、MMCで曲線的で自由な形状表現を可能にするという趣旨の研究は行われており[8-10]、今後、様々な問題への応用が期待できます。
MMCの構成要素を数学的に記述する方法
このような概念に基づいてトポロジー最適化をする場合、設計領域上で構成要素が存在する領域をどのように数学的に表現するのかという疑問が浮かびます。以降でこの疑問について説明していきます。
前述の通り,MMCのi番目構成要素d_iは構成要素の中心座標(X_0,Y_0)、長手寸法L、短手寸法t,回転角度θの5つです。
\begin{align*}
d_{i}
=
\left[
\begin{array}{ccc}
X_{0} & Y_{0} & L& t & θ\\
\end{array}
\right]
\end{align*}
これら5つの設計変数を用い、構成要素の有無は
φ(X,Y)>0⇔(X,Y)∈Ω
φ(X,Y)=0⇔(X,Y)∈∂Ω
φ(X,Y)<0⇔(X,Y)∈D/Ω
ただし、
φ(X,Y)=1-\left(\frac{cosθ(X-X_0)+sinθ(Y-Y_0)}{L/2}\right)^m-\left(\frac{-sinθ(X-X_0)+cosθ(Y-Y_0)}{t/2}\right)^m
という陰関数φで表されます。ただし、mは偶数の定数です。1行目から順に見ていきましょう。
まず、1~3行目は、φが正の座標は構成要素が存在する領域、φが0の座標は構成要素の境界、φが負の座標は構成要素が存在しない領域を表すことを示しています。このように、MMCでは、構成要素の存在をトポロジー記述関数と呼ばれる陰関数φの正負で陰的に表現します。
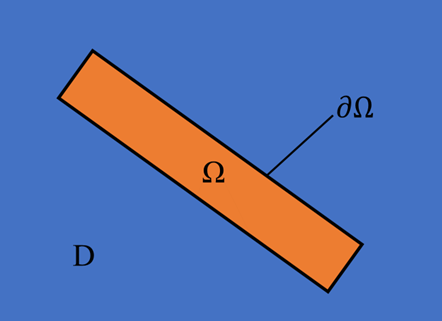
次に、4行目のφが具体的に何を元としている関数なのかを説明します。
はじめに、長径がa、短径がbの楕円の方程式を考えてみます。
\left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2=1
この楕円を拡張した概念に、超楕円(ラメ曲線)があります。超楕円とは,楕円の累乗部分が2以外の偶数値も取れるよう拡張した関数であり、mの値を増加させるにつれて徐々に長方形に近づいていきます。後ほど行う実装ではm=6と設定しました。
\left(\frac{x}{a}\right)^m+\left(\frac{y}{b}\right)^m=1
⇔1-\left(\frac{x}{a}\right)^m-\left(\frac{y}{b}\right)^m=0
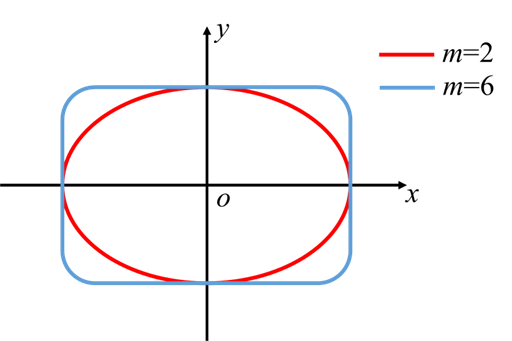
上記の超楕円の式は閉曲線を表しているため、x、yの関数とすることで、閉曲線の内側、外側、境界線をψの値で指し示すことが可能となります。
ψ(x,y)=1-\left(\frac{x}{a}\right)^m-\left(\frac{y}{b}\right)^m
ここで、ψは超楕円の中心に固定された局所座標系x、yで定義された関数です。超楕円の並進・回転を実現するために、全体座標系にψを座標変換し、これをφと定義します。
\begin{bmatrix} x \\ y \end{bmatrix}=
\begin{bmatrix}
cosθ & sinθ \\ -sinθ & cosθ
\end{bmatrix}
\begin{bmatrix}
X-X_0 \\ Y-Y_0
\end{bmatrix}=
\begin{bmatrix}
cosθ(X-X_0)+sinθ(Y-Y_0) \\ -sinθ(X-X_0)+cosθ(Y-Y_0)
\end{bmatrix}
φ(X,Y)=1-\left(\frac{cosθ(X-X_0)+sinθ(Y-Y_0)}{a}\right)^m-\left(\frac{-sinθ(X-X_0)+cosθ(Y-Y_0)}{b}\right)^m
以上でトポロジー記述関数を導出することができました。
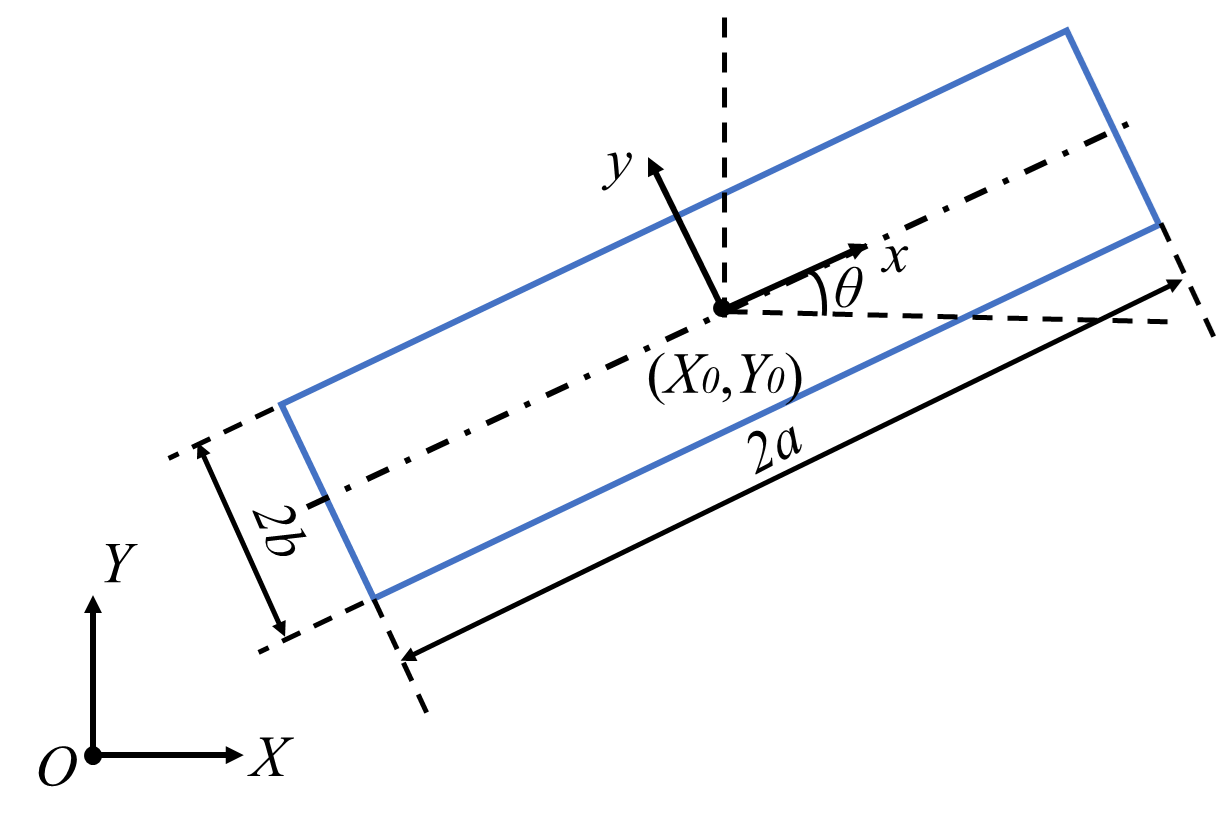
後ほど実装するプログラムの解析では、トポロジー記述関数のX,Yに各有限要素節点の座標を入力し、材料の有無を調べます。そして、有限要素の周囲4節点のトポロジー記述関数値から、その節点が構成する有限要素の剛性を決定し、解析を行います。
トポロジー最適化の実装
最適化問題設定
ベンチマーク問題として、以下のような問題設定でトポロジー最適化を行いました。
・境界条件:片持ち
・荷重条件:自由端中央に垂直荷重
・目的:平均コンプライアンス最小化
・制約条件:設計領域の40 %体積制約
なお、最適化の繰り返し計算は収束状況に関わらず200回目まで行いました。

密度法による最適化結果
密度法による初期幾何形状、最適化後の幾何形状を示します。
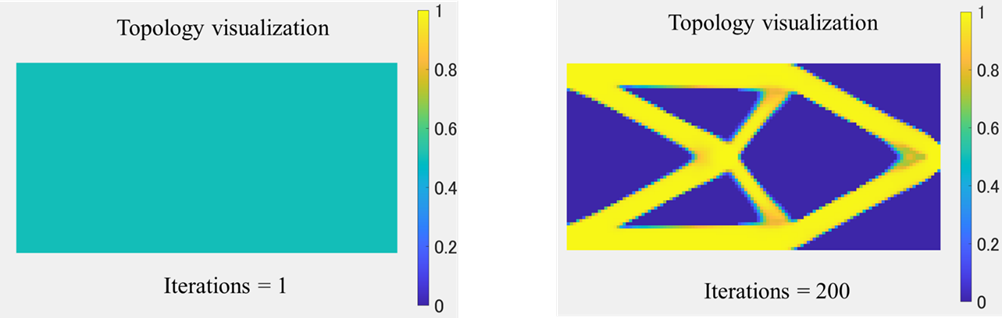
120×60と要素分割数を細かく設定したため、明瞭に幾何形状を表現できています。試しに要素分割数を60×30にしてみましょう。幾何形状の解像度が粗くなっていることを確認できます。

また、感度へのフィルタリングを行わない場合も試してみましょう。要素の有無が交互に並ぶチェッカーボード現象を確認できます。
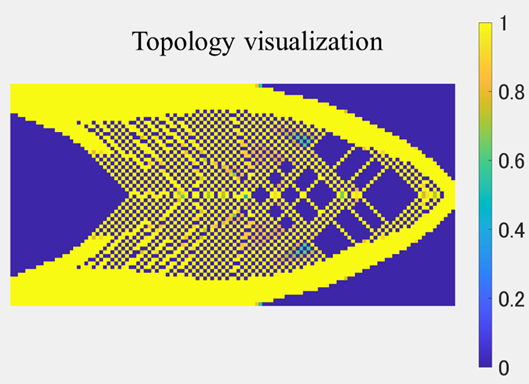
MMCによる最適化結果
MMCによる最適幾何形状と各構成要素を見やすくするために構成要素の塗りつぶしを無くした図を示します。なお、構成要素の数や初期配置については様々な決定方法が考えられますが、今回は先行研究に倣い、なるべく構成要素が設計領域内で均等に配置されるよう、16個の構成要素を斜めに交差させ敷き詰めました。
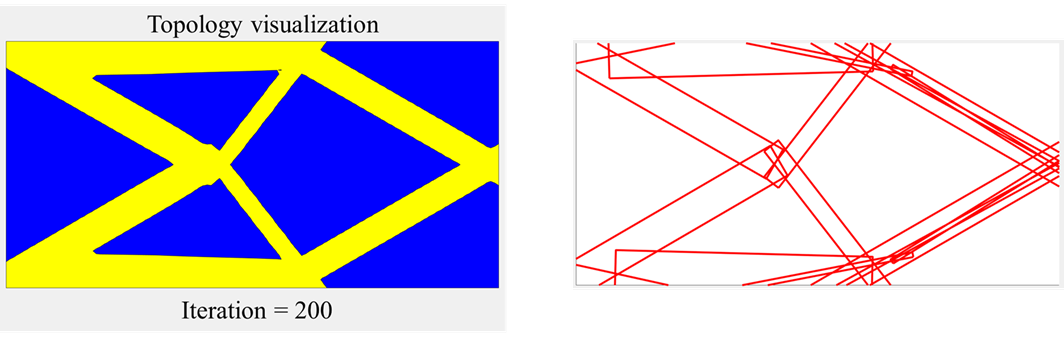
どのように最適幾何形状が創出されたのかを確認するために最適化Iterationが1、10、30のときの結果を示します。

このように、各構成要素が徐々に最適幾何形状に適合していることがわかります。
前述の通り、幾何形状の表現が有限要素の数から独立しているので、メッシュをある程度荒くしても幾何形状の創出に影響はありません。これを確認すべく、有限要素数を60×30としたときの結果も見てみましょう。
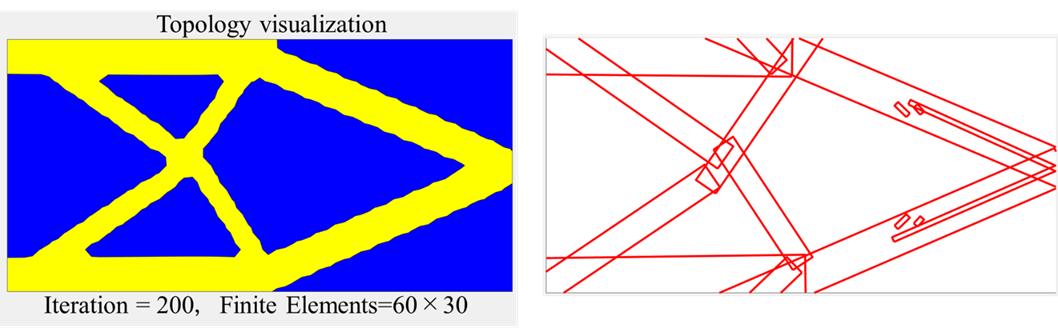
このように、メッシュを荒くしても同傾向の幾何形状を明瞭に表現可能なことが確認できました。
次に、創出された幾何形状と計算コストの観点から両手法の結果を比較したいと思います。
創出された幾何形状の比較
両手法で創出された幾何形状を比較します。
密度法により創出された幾何形状は表現に制限が無いため、滑らかに幾何形状を表現できています。
一方で、MMCは長方形の構成要素の集合で幾何形状を表現するため、構造的特徴は密度法による結果と一致しているものの、洗練されていない幾何形状になっていることがわかります。
具体的には、構成要素同士の連結部分の不連続さや、構造上不要と思われる突起が表れてしまっていることが挙げられます。
理由としては、構成要素同士の連続性に何の拘束も課されていないこと、構成要素の変化は目的関数の感度にのみ依存しており、図に示す突起のように微小な部分は感度へ与える影響も微小で、最適化の中で修正すべき部分として感知されないことが考えられます。

今回解いたShort beamのベンチマーク問題で得られる幾何形状はそのほとんどが直線形状で構成されていましたが、最適幾何形状がより複雑な曲線形状を含んでいる問題の場合、密度法とMMCの幾何形状表現の差がより顕著に表れるでしょう。
計算コストの比較
有限要素数が120×60、60×30のときの密度法とMMCの計算コストについて、有限要素数、設計変数の数、計算時間、各計算時間の割合を表にまとめます。
密度法の設計変数の数は有限要素数と同じ7200個と1800個、MMCは構成要素数を16個としたため、設計変数の数は有限要素数によらず80個です。MATLABの時間計測機能により、最適化Iterationが200回終わるまでの計算時間を計測しました。
| Method |
Finite elements |
Design variables |
Time [s] |
Ratio [%] |
| Density method |
120×60 |
7200 |
293.2 |
100 |
| Density method |
60×30 |
1800 |
59.2 |
20.2 |
| MMC |
120×60 |
80 |
31.3 |
10.7 |
| MMC |
60×30 |
80 |
13.9 |
4.7 |
表の通り、計算時間は密度法とMMCで比較すると大きな差があることがわかりました。
先ほどお見せした、創出される幾何形状の解像度が低い60×30の密度法でも、120×60のMMCよりも約2倍計算コストがかかるとわかります。
このように、幾何形状の表現自由度の観点では密度法が、計算コストの観点ではMMCが優れていることがわかり、一概にどちらが優れていると言えるわけではありません。
例えば、製造制約から単純な幾何形状を創出したい場合や、最適幾何形状のおおよその傾向を確認したい場合はMMCのような簡易的手法が良く、複雑な幾何形状の特徴を詳細に把握したい場合には密度法のようなフルサイズのトポロジー最適化が適しているでしょう。
おわりに
本記事では、密度法、均質化法、レベルセット法、MMCの4つのトポロジー最適化手法について特徴を紹介し、密度法とMMCを実装した結果を比較しました。両者とも長所と短所があり、製造方法や扱う物理現象、設計制約によって使い分ける必要があることを説明しました。
今回はトポロジー最適化手法自体に焦点を当てて説明をしましたが、実問題に適用する際に最も重要なことは、
・設計対象をどのようにモデル化し、いかに最適化として解ける問題に落とし込むか
・最適化結果を人間がどのように解釈し、いかに製品として形にするか
です。
実問題においては、モデル化や使用する最適化手法によっては無意味な幾何形状が創出されることもしばしばあります。また、トポロジー最適化結果をそのまま設計結果とすることは現状難しく、コンピュータと人間が連携しながら製品として形にすることが必要となります。
弊社の強みはまさにここにあり、モデル化や手法の選択、結果を解釈し形にすることにおいて様々な知見やノウハウを保有しています。例として、トポロジー最適化を用いて設計を行っている技術記事を是非ご一読ください。
熱流体位相最適化によるヒートシンク設計事例の紹介
設計事例 : 自動車向けロアアーム
本記事では構造強度に関する単純なベンチマーク問題を扱いましたが、実問題にいくつかのトポロジー最適化を適用した際の結果の差異についてもいつか紹介したいと思います。
皆さんもトポロジー最適化をご自身で実装し、各手法の仕組みや結果を比べてみてください。新たな発見があり、理解が深まることと思います。
参考
[1] Bendsøe, M. P., and Kikuchi, N., “Generating Optimal Topologies in Structural Design Using a Homogenization Method,” Computer Methods in Applied Mechanics and Engineering, Vol. 71, No. 2, 1988, pp. 197–224.
[2] Dorn, W., Gomory, R. and Greenberg, H., “Automatic Design of Optimal Structures,” Journal de Mecanique, Vol. 3, No. 6, 1964, pp. 25–52.
[3] Bendsøe, M. P., “Optimal Shape Design as a Material Distribution Problem,” Structural Optimization, Vol. 1, No. 4, 1989, pp. 193–202.
[4] Sethian, J. A., and Wiegmann, A., “Structural Boundary Design via Levelset and Immersed Interface Methods,” Journal of Computational Physics, Vol. 163, No. 2, 2000, pp. 489–528.
[5] Guo, X., Zhang, W. S., and Zhong, W. L., “Doing Topology Optimization Explicitly and Geometrically-A New Moving Morphable Components Based Framework,” Journal of Applied Mechanics, Vol. 81, No. 8, 2014, p. 081009.
[6] 日本計算工学会 編,「トポロジー最適化」,丸善出版,2013.
[7] 近藤 継男,矢地 謙太郎,西脇 眞二 共著,「トポロジー最適化の基礎 弾性体ならびに熱流体工学諸問題への応用のために」,コロナ社,2024.
[8] Zhang, Z., Yuan, J., Zhang, J., and Guo, X., “A New Topology Optimization Approach based on Moving Morphable Components (MMC) and the Ersatz Material Model,” Structural and Multidisciplinary Optimization, Vol. 53, No. 6, 2016, pp. 1243–1260.
[9] Guo, X., Zhang, W., Zhang, J., and Yuan, J., “Explicit Structural Topology Optimization Based on Moving Morphable Components (MMC) with Curved Skeletons,” Computer Methods in Applied Mechanics and Engineering, Vol. 310, 2016, pp. 711–748.
[10] Otsuka, K., Dong, S., Kuzuno, R., Sugiyama, H., Makihara, K., “Moving Morphable Multi Components Introducing Intent of Designer in Topology Optimization,” AIAA Journal, Vol. 61, No. 4, pp. 1720–1734.