発想 idea
先日、家にオリーブの木が届きました。
引っ越し祝いに職場の方から頂いたものですが、育て方を調べている過程で、オリーブというのは1000年以上も生きることができる「長寿の木」であることを知りました。世界最古のオリーブは、ギリシャのクレタ島に生えているOlive tree of Vouvesと呼ばれている古代のオリーブであり、樹齢は少なくとも2000年から3000年であると言われています。我が家のベランダに置いたオリーブの木を眺めながら、「私だけでは1000年も育てることはできないけど、今後どんなふうに成長するのだろうか」と空想にふけりました。
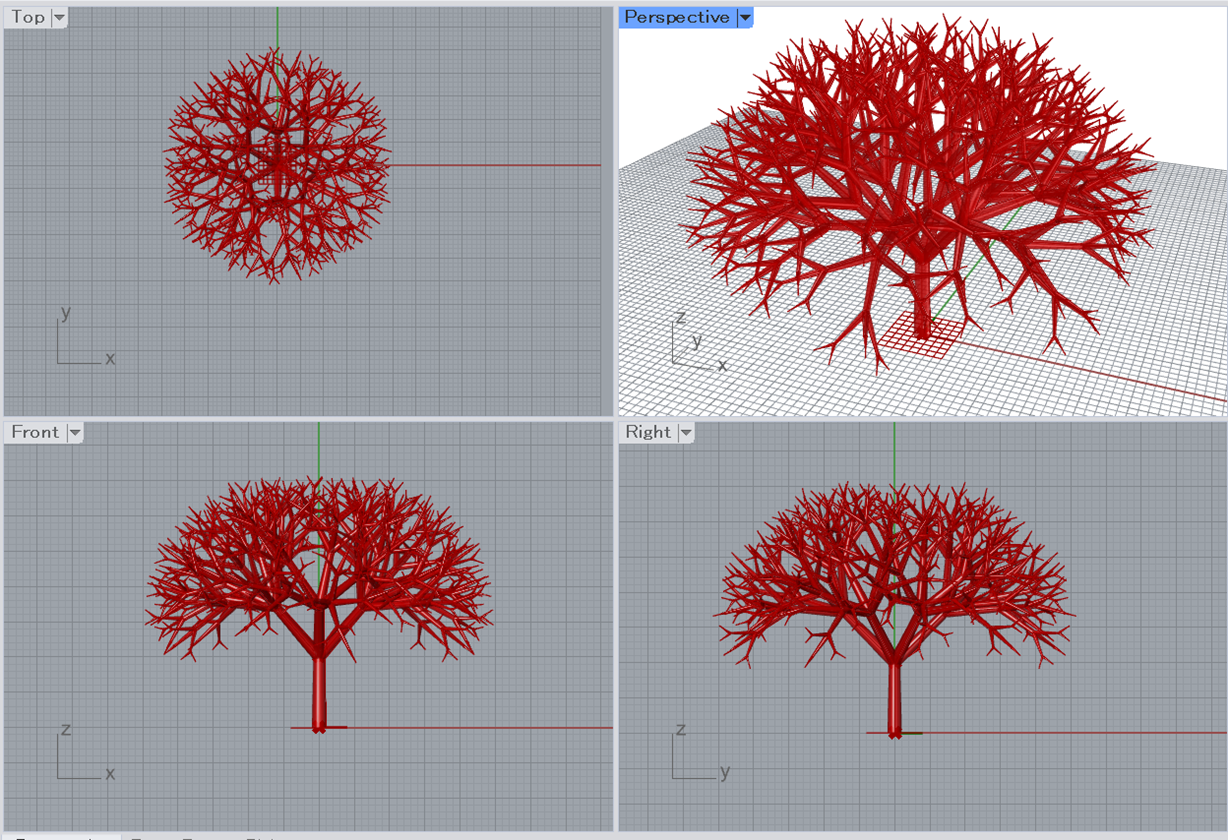
話は変わって、弊社でも使用している3D CADであるRhinocerosでは、再帰性処理による構造作成の例として、良く樹形のモデリングがチュートリアルに使用されます。下図は、サンプルコードがたくさん載っている書籍[1]の例に従って再帰性処理により作成した樹形になります。このように、先端に向けて相似形状を繰り返しながら生成された構造を「フラクタル構造」と呼びます。
フラクタル構造は、幾何的な形状であり、大変美しく見えますが、一方で自然に生えている木と比較すると何か違和感を覚えます。今回は、再帰性処理による構造作成の方法をおさらいしながら、より自然な樹形を目指して、RhinocerosのGrasshopper上で樹木形状のモデリング環境を作成してみたいと思います。
調査 research
自然な樹木の幹形状に関する研究は、コンピュータグラフィックス(CG)の発達とともに、研究が進んできたテーマです。これらの研究のモチベーションは、建築計画における景観シミュレーション、映画、マルチメディアコンテンツ、バーチャルリアリティー等で、見た人にリアルな体験を与えることです。昨今、話題となっているメタバースが普及すれば、人間が違和感なく自然と感じられる要素を表現する方法は、より重要になってくる気がしますね。
自然な樹木生成についての文献としては、以下の論文を参考にさせていただきました。
金丸ら[2]は、葉がなるべく光を受けるように枝先の方向が変化する「向日性」による枝先方向の修正モデルを適用し、自然な樹木に見られる樹冠や枝垂れの性質を再現しました。
吉澤ら[3]は、伸長指向と葉面積拡張指向の2つの分枝モデルを組み合わせるとともに、群生による樹木同士の成長における相互作用を検証しました。
同じく、吉澤ら[4]は、植物の生育する環境である地形や周囲の建物がつくる影日向の分布をマッピングし、生育環境に適応して樹木が成長する様子を再現しました。
大志田[5]は、目に見える地上部だけではなく、地中の根の成長モデルと合わせて成長シミュレーションを行い、相互作用による成長への影響を検討しました。また、質点ーバネモデルを用いた外力による樹木へのストレス値(=応力)により樹木の幹が肥大化する現象を表現し、樹齢の長い樹木の印象を与える方法を模索しました。
これらの文献をもとに重要と思われる考え方を以下の3点に整理しました。
- 分枝モデル:世代が進むごとに、枝がどのように分岐して伸びていくのかを定義する。
- 向日性:光の取り合いにより、枝同士、樹木同士が相互に影響を受け自然に分布するとともに、場合によっては枝垂れし、下方向の空間に光を求めて枝が伸びる。
- 幹の太さ:幹の太さは、その幹に与えられるストレス値(=応力)の大きさによって決定する。
構築 build
それでは、樹木のモデリングを始めていきましょう。モデリングはRhinocerosにデフォルトで付属したプラグインであるGrasshopper上で実行していきます。Grasshopperとはなにか?については、過去に記事で取り上げているので、より深く知りたい方はこちら(【Rhino+Grasshopperを理解して魔改造しよう】)の記事もおすすめです。
Anemone
元の枝の情報を使って新しい枝の形状を決定する再帰処理を、Grasshopper上で実行するために最初にご紹介した書籍[1]でも使用されていた、Grasshopperプラグインである「Anemone」を導入します。
Grasshopperでは、入力に対して一定の処理をして出力する機能を持った、様々なコンポーネントをつないでいくことで複雑な処理を可能にします。これらのコンポーネントは、左から入力して、右から出力するというお約束があり、左から順に処理されていくため、出力を再度利用するループを作ってしまうと自己参照が発生してしまいデフォルトの状態では、エラーになってしまいます。そのため、再帰処理をデフォルトのまま書こうとすると、同じコンポーネントのセットを繰り返し記述する必要があるため、右へ右へとコードが伸びていってしまいます。
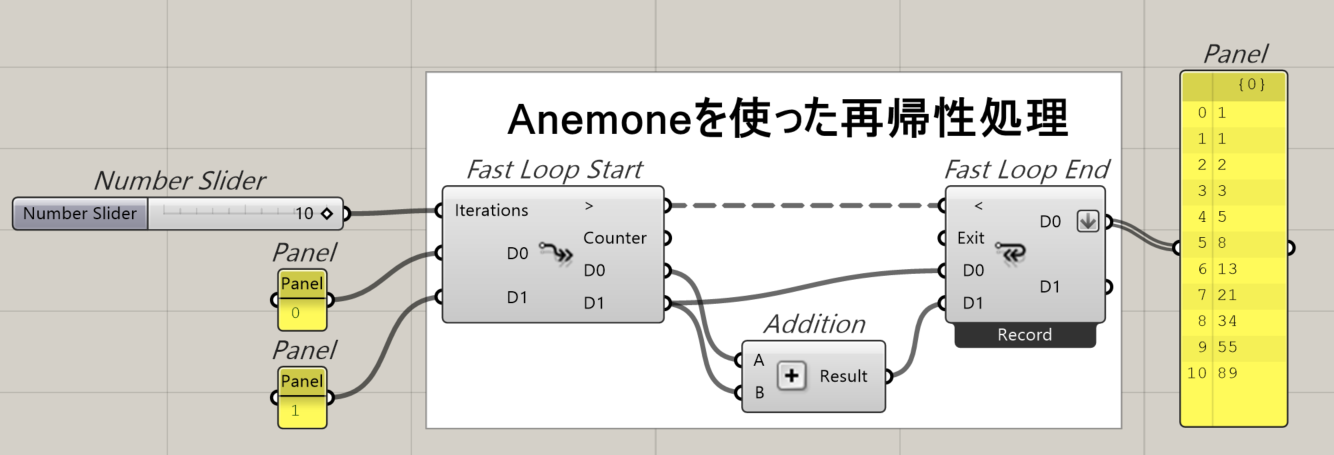
「Anemone」を使用すると、以下のサンプル画像のようにループによる自己参照が簡潔に記述可能となり、周回ごとに前ステップの数値を参照することができます。今回は、このAnemoneによるループ1周期を1世代とし、世代ごとに元の枝の先端に新しい枝が分岐して伸びるという処理を繰り返します。
二分枝モデル
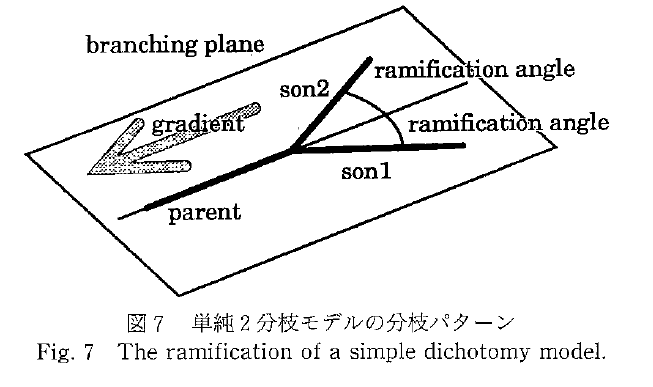
実際の植物を観察すると枝分かれの方法は多岐にわたります。枝の生え方にルールなどないように見えますが、根本となる幹が1本であり、先に向かうほど枝の数が増えていくのが自然でしょう。この性質を最も単純に表したのが、2分枝モデルであると言えます(下図、文献[2]より引用)。このモデルでは、元の枝を表すラインが乗る平面を定義し、その平面上で元の枝の先端から一定の角度、一定の長さで新しい枝が2本発生するという方法を繰り返すことで樹木の成長を表現します。
向日性
単純な二分枝モデルを採用して、Anemoneを用いた再帰性処理により8世代まで計算を行って出力した樹形が下図になります。この時点では、まったく自然な樹木には見えません。茶道で使う茶筅のように見えます。原因は、周りに十分なスペースがあるのになぜか枝が密集して規則正しく並んでいるためです。
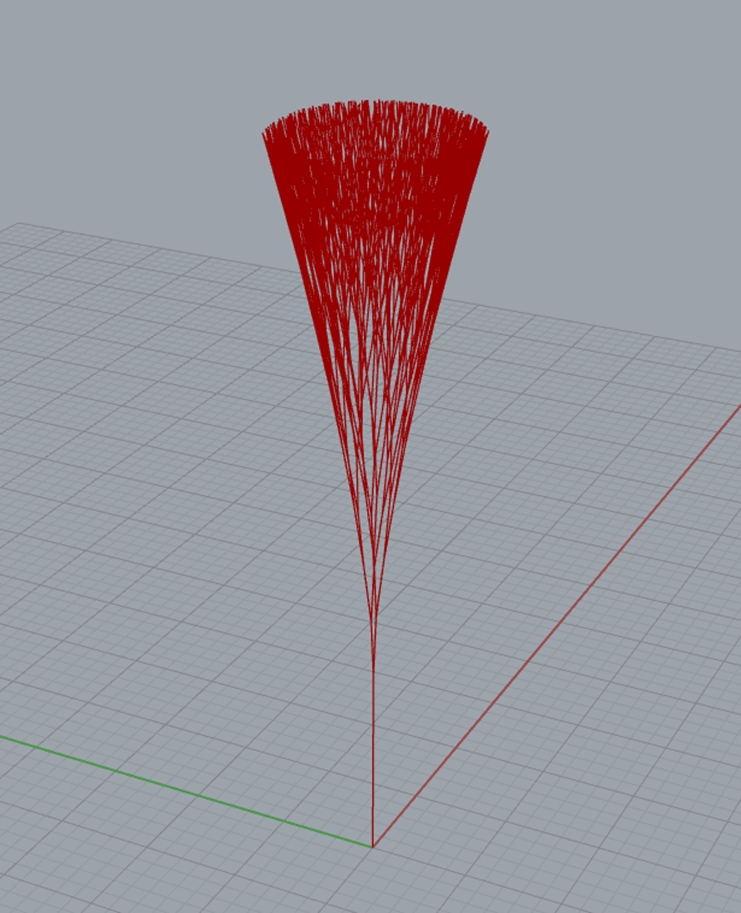
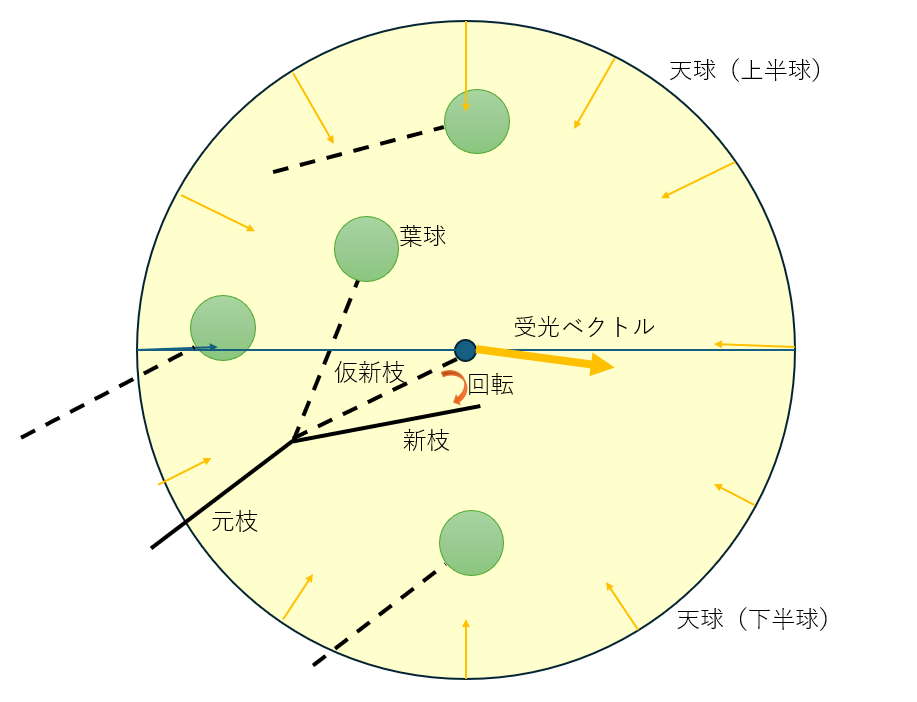
そこで文献[2]で提案されている向日性モデルを採用します。このモデルでは、新たに生成されたすべての枝の先端に葉球とよばれる日差しを遮る領域を定義し、ある枝先が全方向から受ける光のベクトルを合計して得られる受光ベクトルの方向をもとに、枝先の方向修正します。ある枝先から見た時に、ほかの枝先がある方向は葉球にが光を遮るため、そちらの方向には伸びたくないという力が働きます。これにより、それぞれの枝が、光を多く受けられる位置を探索し、枝先の密集を回避する向日性を表現することができます。
ベースとなる日照量は、上半球の光が強く、周囲や地面からの反射光を想定している下半球は0.7倍程度の光量としています。したがって、周りに何もない自由な空間であれば枝先は徐々に直上に向かって伸びる性質を持ちます。
2分枝モデルに向日性を追加して第8世代まで計算を行って出力した樹形が下図になります。大分マシになりましたが、まだ少し不自然です。

ランダム枝枯れ
向日性を入れたとしても、1本の垂直幹からシミュレーションを開始すると、完全な対照形状の樹木が成形されてしまいます。実際の自然では、風や雨などの外部要因により、傷ついた枝が枯れてしまうこともあるでしょう。ここでは、一定の確率で新枝が枯れてしまうランダム性を導入し、樹木に非対称性を与えて自然な樹形を再現します。枝が枯れることによって、そのスペースには光が余ることになるので、向日性により、周りの枝が集まってきてそのスペースを埋めるような挙動が見られるはずです。
向日性とランダム枝枯れを追加して生成した樹木が下図になります。どうでしょうか、なかなか自然な枝ぶりになってきたのではないかと思います。さらに2本の樹木を同時に生やしてみると、お互いの葉球位置を観測しているために、重なりながらも、枝先はお互いによけるように成長している様子が観測できます。

Tree構造
さてここまで、自然な樹形を目指して、樹木の成長モデルを改良してきましたが、Grasshopperで取り扱うデータの構造も樹木と似ている点が面白いです。
過去記事(【Rhino+Grasshopperを理解して魔改造しよう】)でも触れられているように、Grasshopper上では、GH_Structureとよばれるデータ構造で値が受け渡しされますが、この構造はDataTreeなどとツリー構造になぞらえて説明されることが多いです。下図はここまでのコードで生成された樹木モデルとその情報を保持しているデータ構造を可視化したものです。DataTree内の{}で囲まれた数値はpathと呼ばれており、それぞれのpathにあるデータはbranch、まさに枝と表現されています。branch内のリストが各枝を表しており、ここでは世代ごとにpathが分かれています。一方で、3Dモデルの枝先に描画したのは、各branchにおけるリスト番号です。これを見ると、同一のbranch内に2本の樹木の枝がごちゃ混ぜに格納されていることがわかります。これだと、2本の樹木の識別ができませんし、後処理でもどの枝がどのデータに対応しているのか把握が難しくなります。
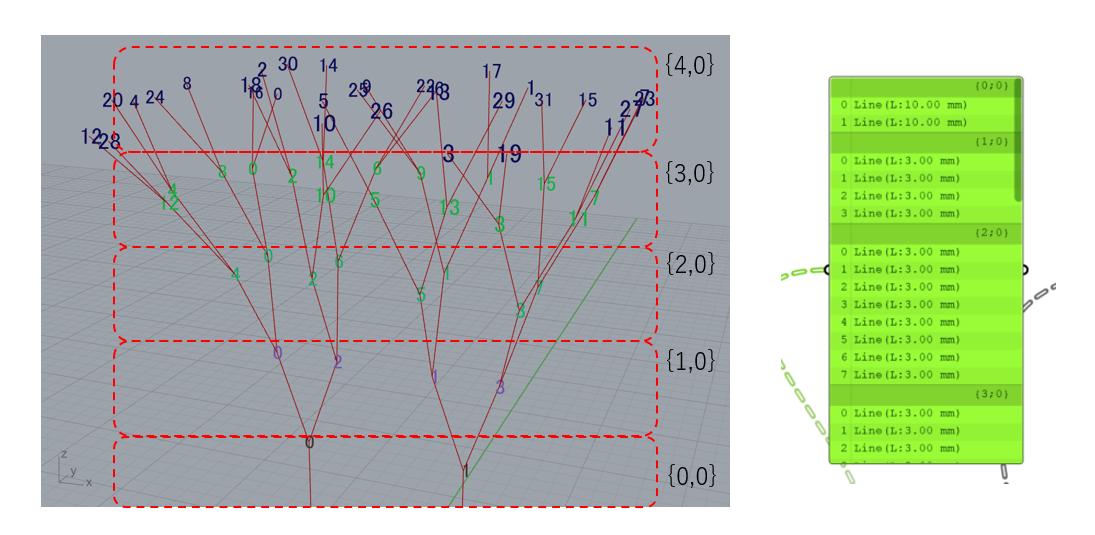
樹木のモデリングとそれを保持するデータ構造(整理前)
そこで、データ構造を下図のように整理しました。pathの一桁目は世代を表し、二桁目が樹木の番号を表します。このように整理すると、ある樹木の何世代目の枝がどのpathにあるのか分かりやすく、リストも0から順に並んでおり大変見通しが良くなりました。特に今回のように再帰性処理により、データ数が自動的に増えていく場合は、データ構造を整理し、どこにどの情報があるのか対応させて整理しておくのが良いですね。
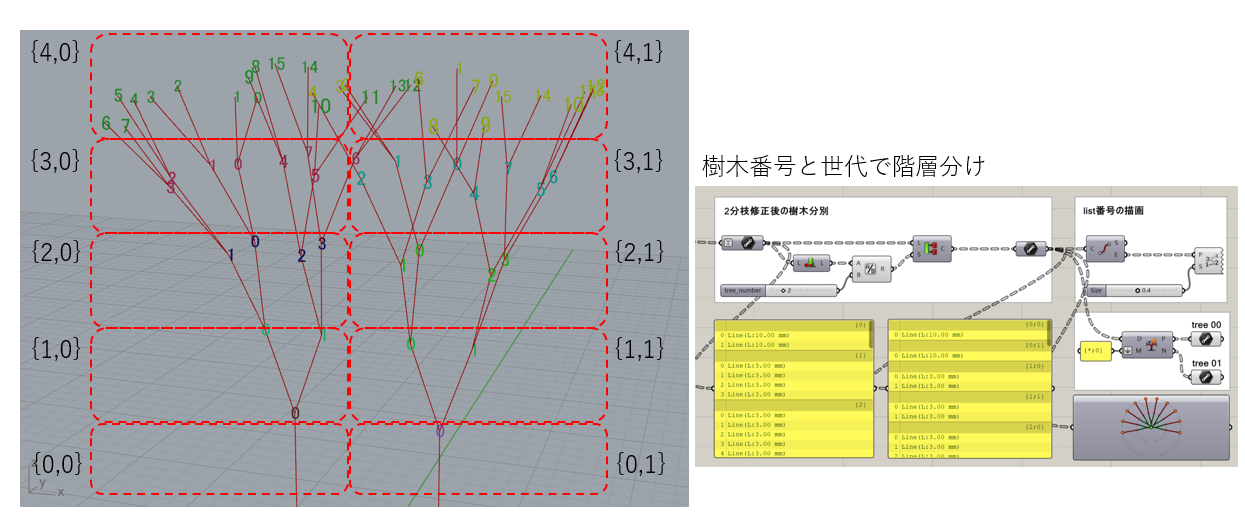
樹木のモデリングとそれを保持するデータ構造(整理後)
幹の太さ Karamba 3D
最後に、こちらの過去記事Karamba3dの性能について考えようでも使用した「Karamba 3D」を使用して樹木の幹の太さを決定します。Karamba3dはGrasshopperで動く構造解析プラグインであり、高速に構造解析できる点が強みとなっています。各枝を梁要素でモデル化し、重力を加味して、各枝にかかる軸荷重を計算し、その荷重を支えられる幹太さになるように木が成長するようにします。接続されている枝の数が多いほど負担する荷重が大きく、また幹から遠方に伸びた枝ほどモーメントがかかるために支える幹は太くなければなりません。
Karamba 3Dの「Optimize Cross Section」を使用すると材料リスト(太さの異なる円柱のWood材料をリストとして定義)の中から必要十分な枝径を選択し、樹木全体で各箇所の軸応力が制限値以下になるように最適な枝径(幹径)を決定してくれます。
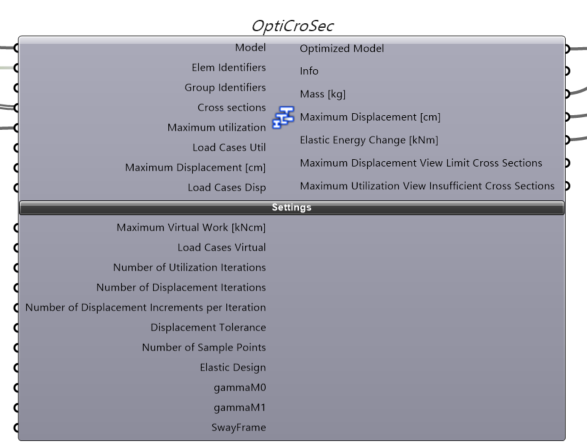
実行 execute
それでは、作成したGrasshopperコードを用いて、樹木を生成してみます。
もととなる幹は、鉛直上向きに生えた直線の枝で隣接して2本の幹を定義しました。これらの幹を第0世代として、第9世代まで成長させます。余談ですが、1世代ごとに枝の本数が2倍ずつ増えていくとともに、一つの枝先に対して、同世代の葉球すべてに対して計算を行うため、(2^N)^2=2^2Nずつ計算量が増えていくので、世代数Nを上げるとそれなりに計算時間がかかります。このケースでの計算時間は20分ほどでした。
世代ごとに枝を描画したgif画像を作ったのでぜひ下をご覧ください。1世代ごとにKaramba 3Dを用いて幹の太さを計算しているので、成長しながら幹が太っていく様子が再現されていて、とてもリアルです。2本の幹を立てただけで、このように木が生えてくるコードができて大変面白いですね。
生成された木を眺めてみると、文献[2]にあった枝垂れを見て取ることができます。また、2本の木の枝がお互いに干渉を避けるように外側や空いているスペースをめがけて伸びているように見えます。同じ世代の枝でも幹の太さが異なるものが見つけられます。これは、より多くの荷重を支えている枝ほど太く成長しているためです。

さらに、初期値となる第0世代の枝の向きを変えるとまた違った表情を見せてくれます。山中の崖や川沿いでは、幹が斜めに生えている木がありますね。下図は第0世代の2本の幹をXY方向に寝かせて解析をしてみた結果です。特に、右の木の第3~第4世代の枝を見ると、向日性の光量ベクトルの向きに従って鉛直上方向に延びようとしているのがわかります。

振り返り review
本記事では、自然な樹木形状の生成について、3D CADのRhinoceross(Grasshopper)を用いたモデリングの手法を探索しました。Karamba 3Dの解析により自然な幹の太さを与えることで、樹木の成長過程に見えるような、自然な成長モデルを作ることができました。初期値である第0世代幹の配置を変えるだけで色々な成長結果を見せてくれるので観察していてとても面白いです。自分でモデリングした構造でありながら、初期状態からは最終形状は予測できないので、感覚的に自分の制御下を離れた自然物のように感じます。
樹木の生え方はさまざまであり、その数理モデルも色々な表現方法があります。今回作成したモデルは、街路樹のようには見えますが、我が家のオリーブには見えませんね。今回の調査範囲では、オリーブの木に関する成長モデルの文献は見つからなかったので、いつか自分の家の木がどう成長するのか予想できるような成長モデルを見つけたいものです。
最後まで読んで頂きありがとうございました。
皆様にも目に入る木々の枝ぶりを、興味深く楽しんで頂けることを願います。

使用したソフト
- Rhinoceross 8
- Grasshopper
- Anemone(https://www.food4rhino.com/en/app/anemone)
- Karamba 3D
参考文献
[1]Parametric Design with Grasshopper 増補改訂版
建築/プロダクトのための、Grasshopperクックブック
[2]向日性による自然な枝振りのシミュレーション,金丸ら,1990
[3]樹木の生長シミュレーション,吉澤ら,2006
[4]光環境を考慮した樹木生長モデリング,吉澤ら,2007
[5]樹木景観のビジュアルシミュレーションに関する研究,大志田,2000

