はじめに
本記事では下記のような読者を想定し、3~4章程度の構成を予定しています。
- Rhinoceros+Grasshopperに興味がある方
- Rhinoceros+Grasshopperを使う上で内部処理に関する理解を深めたい方
- Rhinoceros+Grasshopperを業務/研究/趣味などのために独自拡張して使いたい方
- メタマテリアルを設計して遊びたい方
2章である本記事では、Grasshopperを自ら拡張していくのに理解すべきだが包括的に解説されているのを見ない部分(全体像から内部処理まで)を理解することを目的とします。
素晴らしい学習コンテンツが多く存在しているので、基本的なことはそちらを参照いただく前提で踏み込んだ説明を主とします。
実装に近い話をするので、何かしらのプログラミング言語、できればC#を知っているとより読みやすいかと思います。
Grasshopperとは?
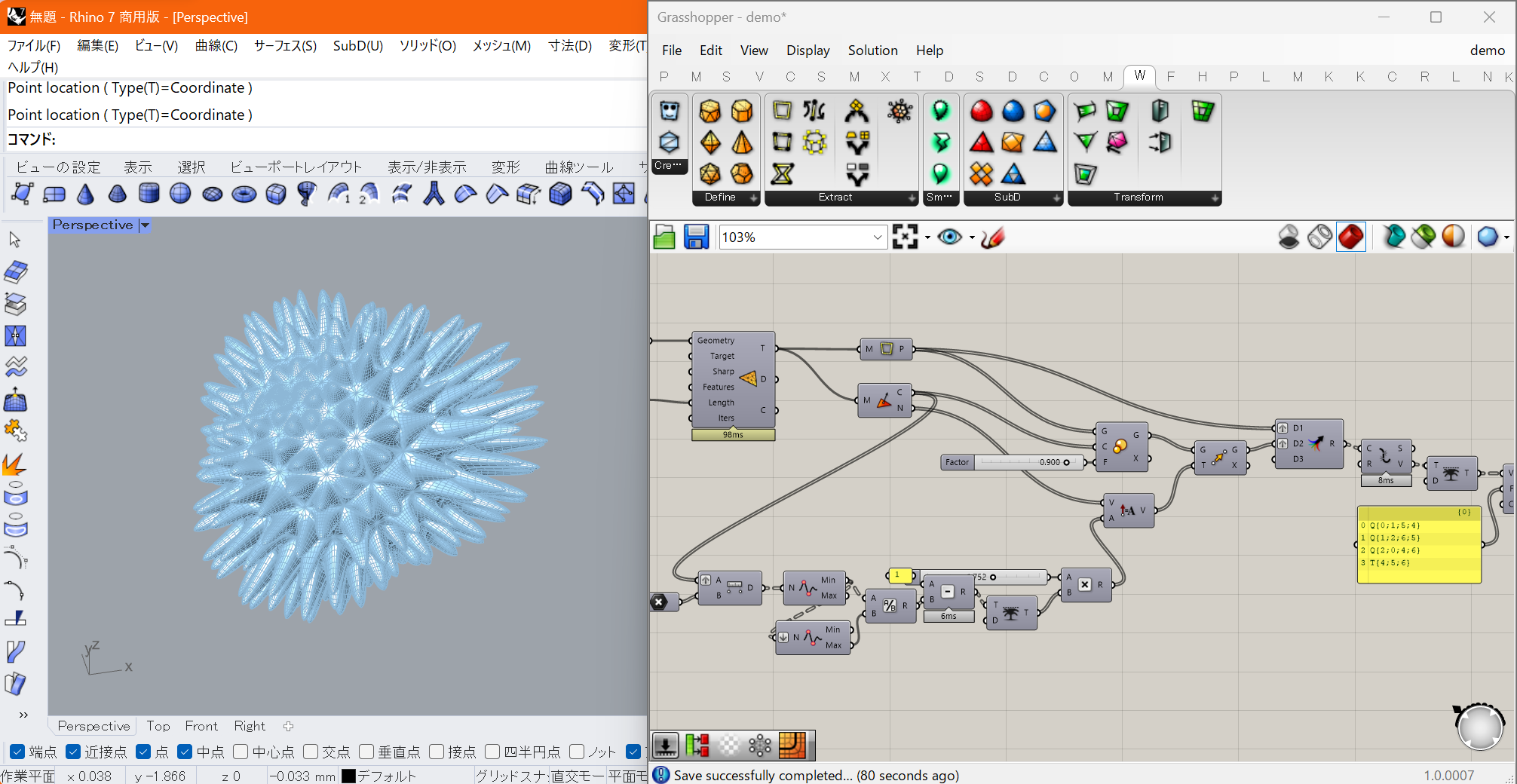
Rhinocerosは前章で述べた通り3DCADですが、Grasshopperはそれにデフォルトで付属したプラグインです。
ノードエディタというビジュアルプログラミング環境を用いて、Rhinoだけでは難しいプログラムでコントロールされた複雑/高度な処理が実現可能です。
雑な説明としては、入力を受け取り処理を行い出力を吐き出すコンポーネント(ノード)を繋げていくことで、そのネットワークの接続関係上手前にあるコンポーネントから順に実行していくものになります。
Grasshopperのうれしさとは?
Grasshopperを使うことの嬉しさは多岐に渡りますが、実際何が嬉しいのかが分からず(かつ妙に複雑なUIのスクショなどを見て)学習の二の足を踏んでいる方もよく見ます。
可能な限り要素分解して紹介をしていきます。
ノーコードで複雑な処理が実現可能
ノードエディタ自体の解説はWikiなどに譲りますが、ノードエディタであることに加え後述する細かい仕様によりプログラムを書かずとも複雑な処理を実現することができます。
独特のデータ構造とアルゴリズムにより直感的かつ複雑な処理構築を可能にしているもののその副作用として独特の理解しづらさもあり、そこを乗り越えることが一つの学習障壁かと思います。
注意点として、Grasshopperはノードの接続関係におけるループの存在を許容しないため直接的には再帰処理が出来ない(!)のですが、後述するデータ構造と処理ルールで再帰処理にあたるような処理を可能にしています。
パラメトリックな処理構築が可能
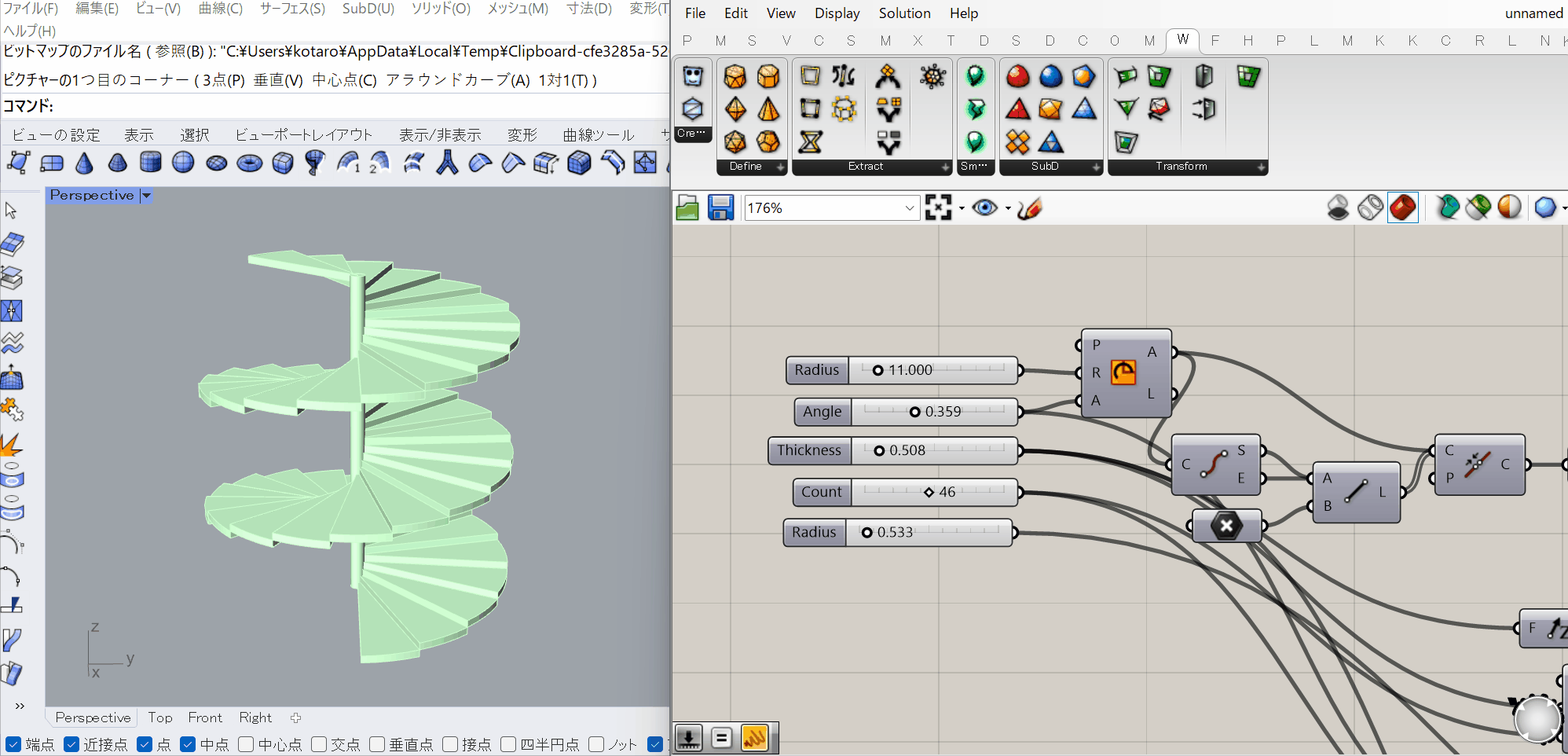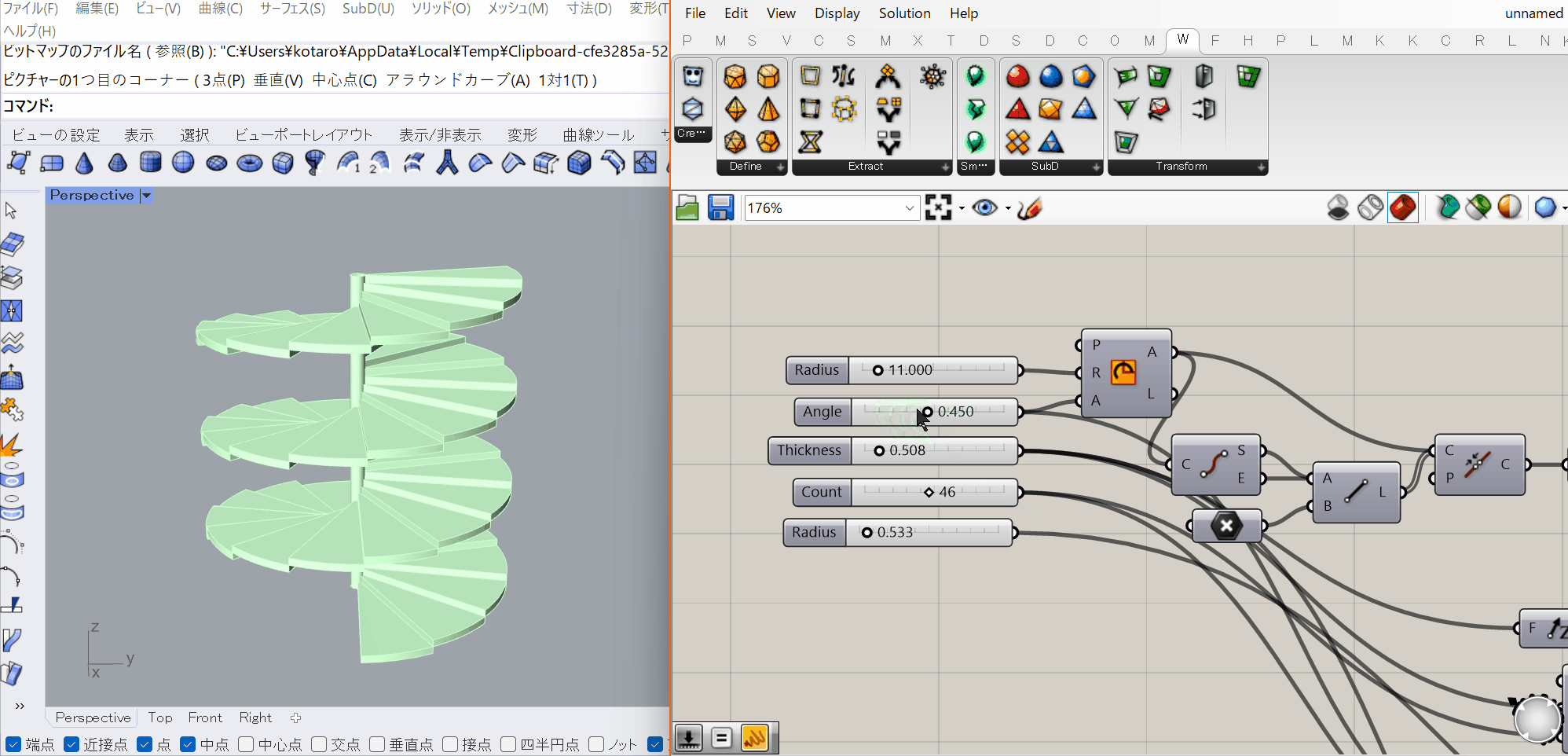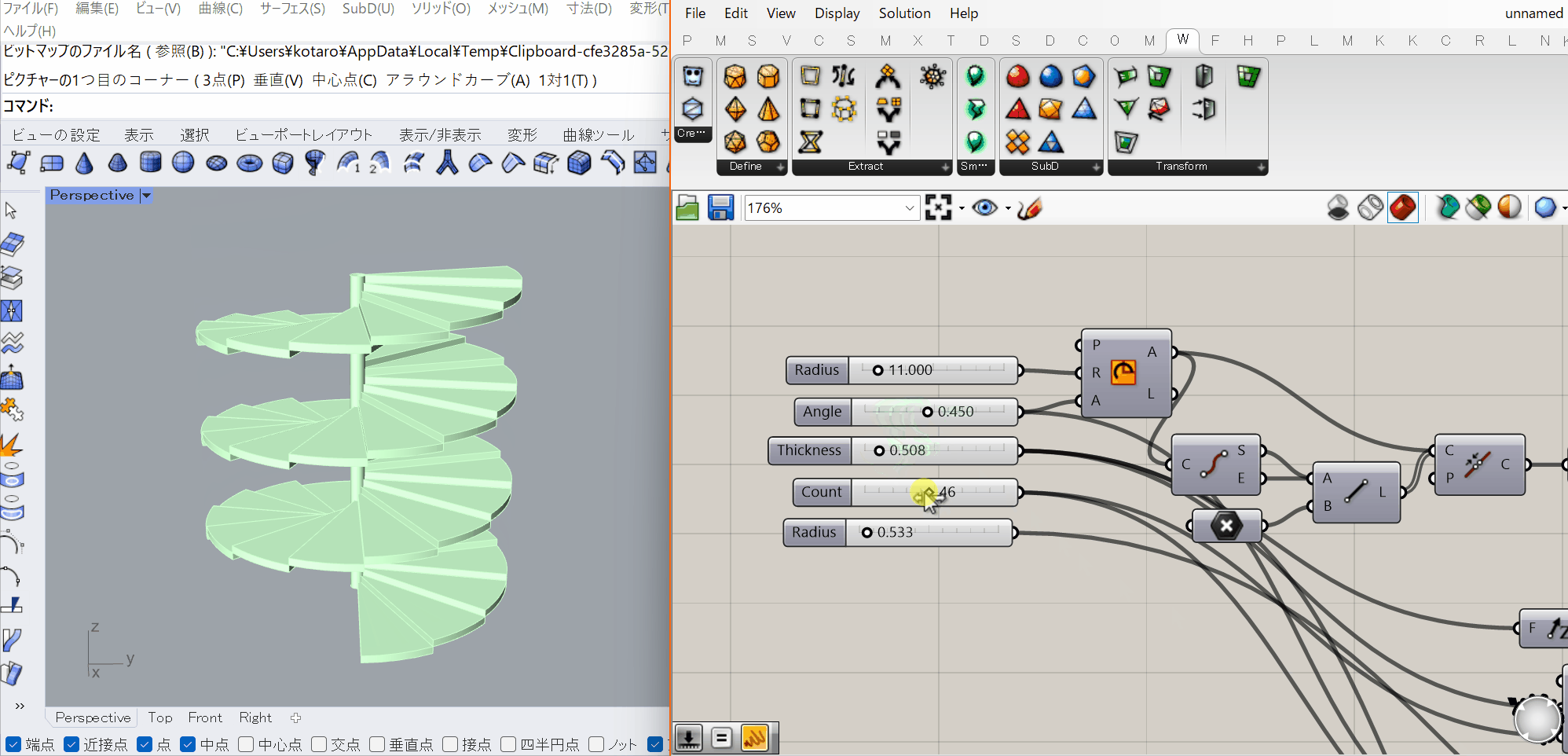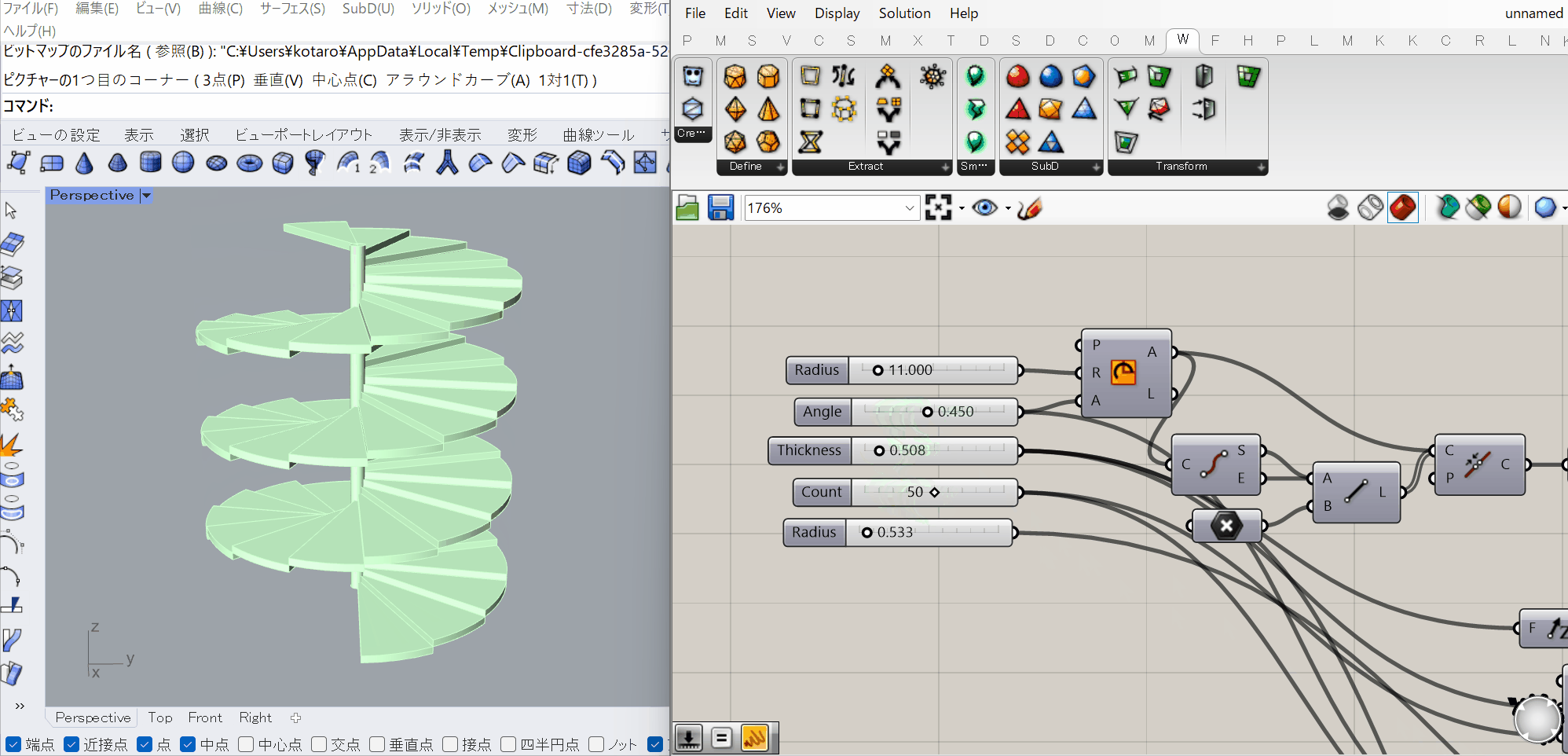
前章で述べた通り、Rhinoはヒストリーを原則的に持たないCADであるため、過去に行った処理のパラメータを後から変更することが原則的に出来ません。
それに対しGrasshopperではパラメータを含む処理のネットワークが構築されるため、パラメータを更新する度にそれが反映された処理が再度実行されます。
Rhinoでインタラクティブに行われる精密な形状編集のようなものはGrasshopperには適していない(ものすごく頑張れば可能)なのですが、
といったパラメータを後から変更したい用途には非常に強力です。
大量/複雑な処理が可能
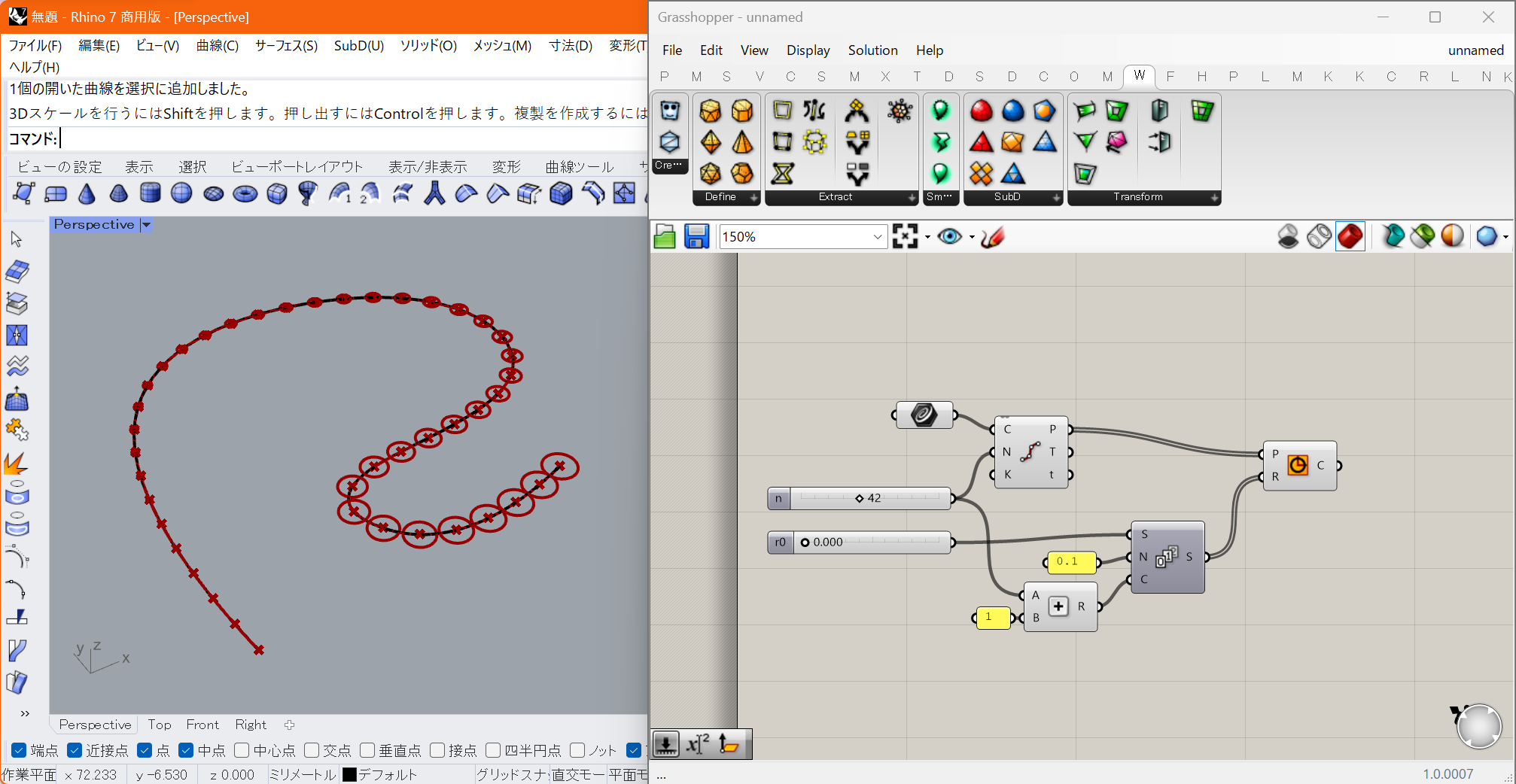
デフォルトでGrashopperから実行できる一つ一つの処理はRhino上でも行えるものが殆どです。
では「与えられた曲線をn等分して得られた各点p_iに、半径がr0+0.1*iである円を作成する」といった処理をRhinoで手作業で行うことは可能でしょうか?
「DivideコマンドでCurveからn+1個の点を得た後、半径を0.1ずつ増やしながらCircleコマンドをn+1回実行する」
ことで実現できますが、気が遠くなります。Grasshopperではコンポーネントを4個程度使えばこれが実現でき、かつ各変数は後から変更可能となります。さらに複雑な例についても同様です。うれしい。
資産の再利用が容易
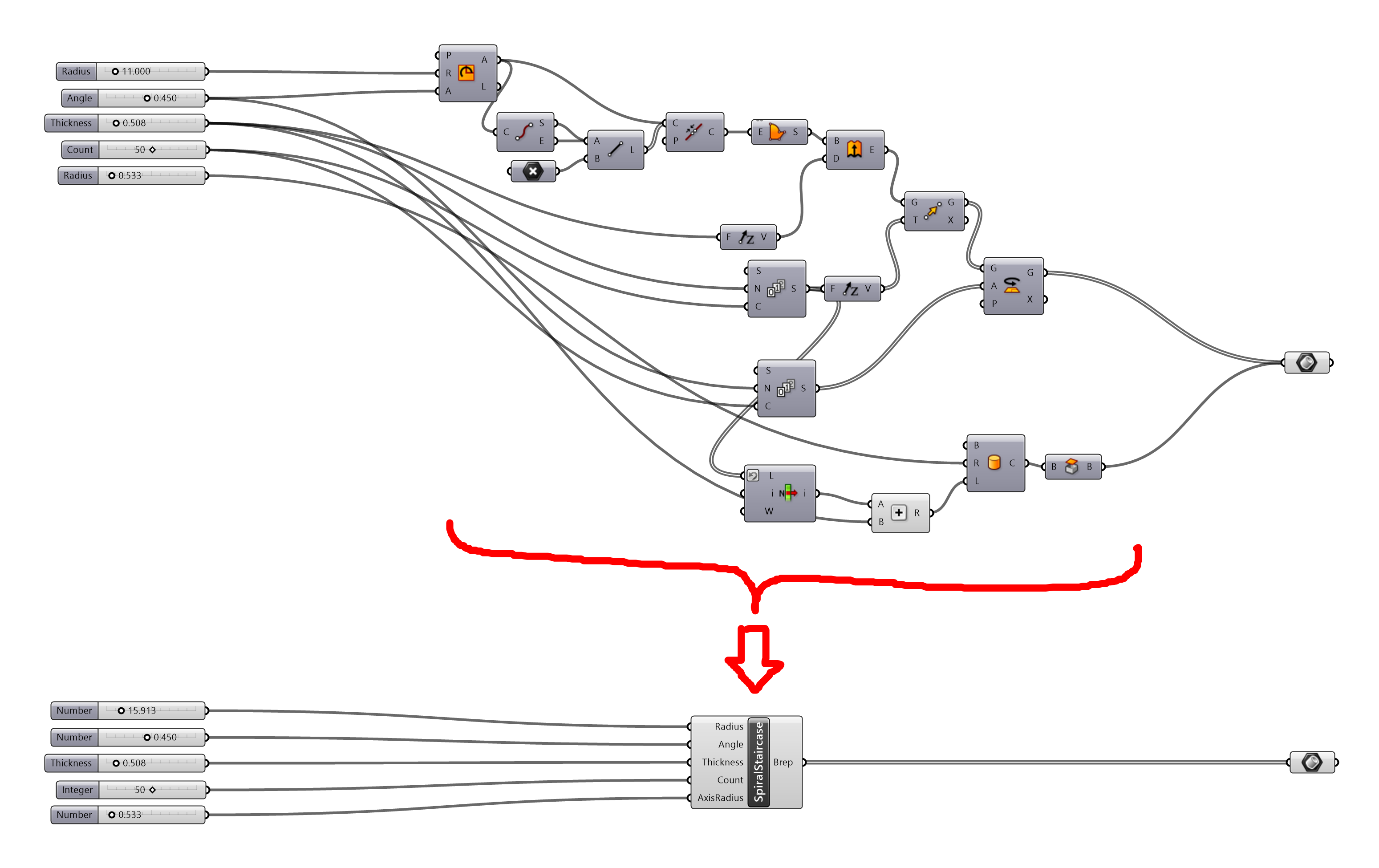
Grasshopperでは、作成した一連の処理やファイルそのものに対して入出力を定義してあげることで、それをノードとして再利用可能にする仕組みが提供されています。
チームでの協働やよく使う処理のモジュール化などに有用です。
拡張性、活発なコミュニティ

前章でRhinoについて述べたのと同様に柔軟な拡張性が担保されており、様々な資産がForumやFood4Rhinoといったコミュニティで活発に公開されています。
基本的にはC#で開発されるアドオンで様々な拡張が可能となり、外部ライブラリの利用も可能です。
また、Grasshopper上ではノードの組み合わせにより処理の構築が行われるためアドオン同士の組み合わせにより業界・技術領域を横断した様々な応用が日々生まれています。
Grasshopperを理解する
Grasshopperを理解する①:基本構成要素
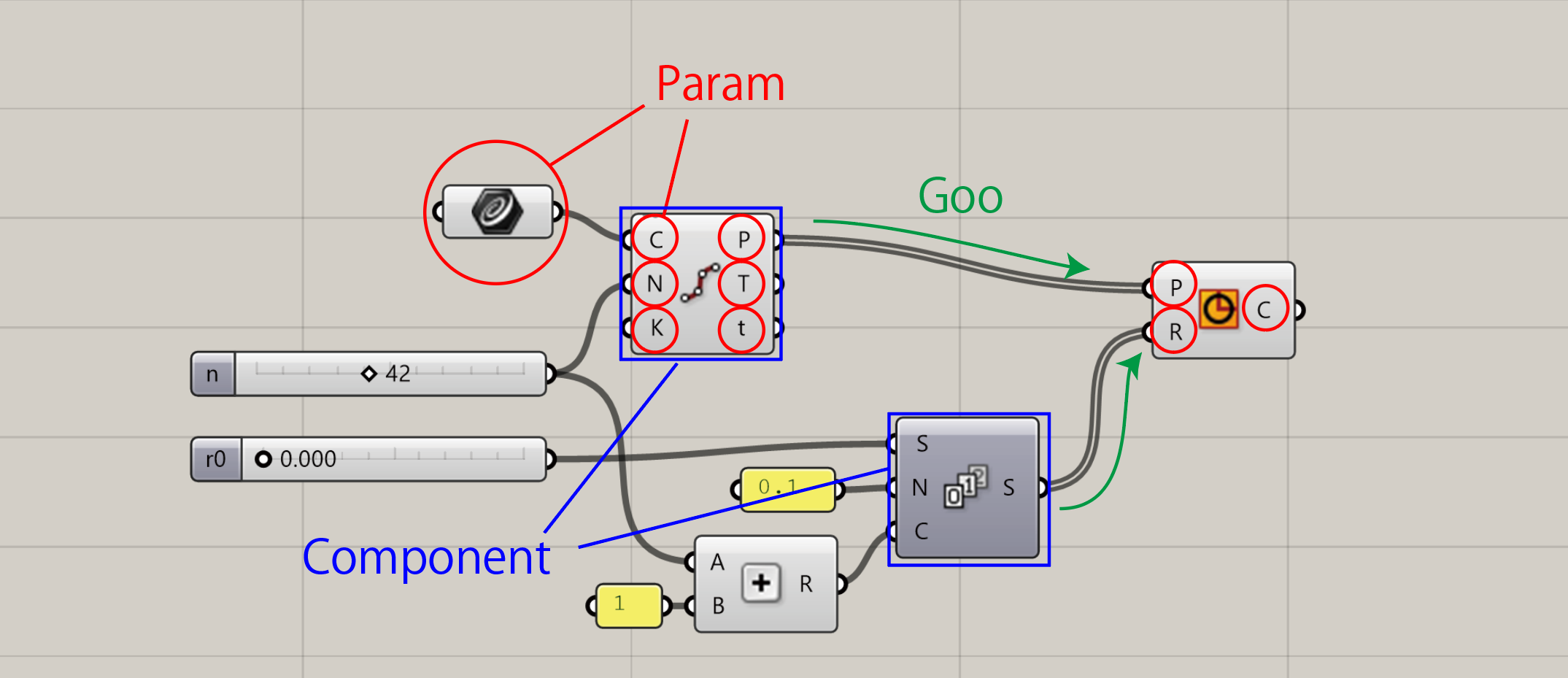
Grasshopperで行われている処理を理解するために重要なのは
の3つの構成要素であり、一言で説明するとGrasshopperは
- データを保持したGooを
- Gooをあるデータ構造で保持可能なParamを介して受け渡ししながら
- Componentで処理を実行
しています。3つについて解説します。
これら3つの機能および関係性を理解することで、Grasshoperで行われている処理の全体像の見通しが立つはずです。
Goo
GH_Goo<T>やGH_GeometricGoo<T>といったIGH_Goo<T>インターフェースを実装する抽象クラスを継承したもので、Grasshopper内で扱いたい型をTに指定したGooクラスを実装することで、Grasshopper内でのハンドリングのための機能を提供する型Tのラッパークラスとして機能します。
Gooが持っている機能は以下です。
- T型の値の保持と外部からのアクセス機能
値のGH_GooおよびGH_GeometricGooはジェネリクスで指定した型の値をm_valueフィールドで保持しており、Fieldプロパティでアクセスが可能です。
- 他のGoo及びクラスとの間での相互変換機能
CastToメソッドおよびCastFromメソッドを実装することで、異なるGoo間での型変換機能を提供することが可能です。
これによりGrasshopperでは、異なる型同士の変換を明示的に意識することなく処理を構築することが可能となっています。
(例:コンポーネントのdouble値を期待する入力ポートにintegerの値を接続しても、内部的にはGH_Intger(GH_Goo<int>)がCastToメソッドを介してGH_Number(GH_Goo<double>)に変換されている)
- 形状の変換機能(GH_GeometricGoo<T>)
RhinoおよびGrasshopperでは、アフィン変換をはじめとする形状の変換が多く行われます。
TransformメソッドおよびMorphメソッドを実装することで、デフォルトでサポートされていない形状データをRhinoおよびGrasshopperの様々な形状変換機能に対応させることが可能となります。
Param
GH_Param<T>やGH_PersistentParam<T>など、IGH_Param<T>インターフェースを実装する抽象クラスを継承(TはGooに制約されている)したもので、1つないし複数のGooをGH_Structure<T>というデータ構造で保持し、コンポーネント間を受け渡していくことが主な機能になります。
非直感的ですが、画像における赤丸で示されているものはすべてParamであり、UI上での扱いに
- Floating:UI上自身がコンポーネントと同様入出力を持ちGooの受け渡しを行う
- Input:Componentの入力ポートとして機能しGooの受け渡しを行う
- Output:Componentの出力ポートとして機能しGooの受け渡しを行う
の3種類があります。基本的にはInputとOutputとして機能しているものという認識で問題はありません。
Component
ノードエディタにおけるノードで、基本的にはGH_Componentクラスを継承して実装されます。入力Paramから受け渡される情報を適切な組み合わせで実処理メソッドSolveInstranceに受け渡し、処理結果を出力Paramに適切なデータ構造で受け渡します。
Grasshopperを理解する②:処理の流れとGH_Structure
Grasshopperの学習の一番のハードルとよく言われるのが、Paramの情報保持に用いられるデータ構造であるGH_Structure<T>で、このデータ構造とあるルールでComponentの挙動が決定されます。
基本的にDataTreeなどとツリー構造になぞらえて説明されることが多いのですが、それによる誤解や理解しづらさがあると個人的には思っているので、内部処理に近い具体的な説明をしてみます。
GH_Structureとは?
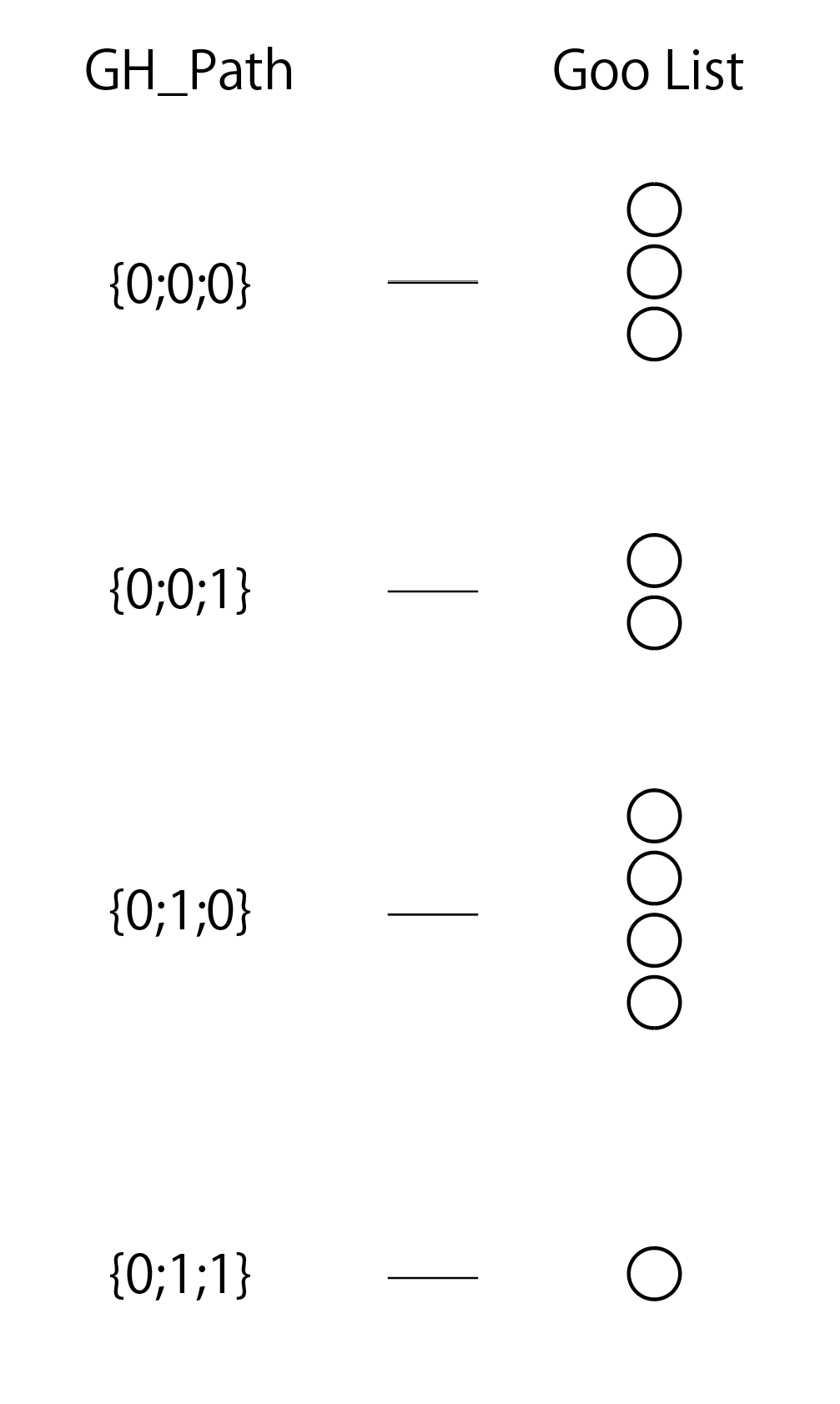
まず、GH_Structureを一言でいうと「GH_Path({0;0;1}のように整数値を複数並べたもの)をキーとしてGooのリストを保持している、GH_Pathにより順序付けされたdictionaryのようなもの」です。
GH_Pathは、左の整数値から順に大小を比較していくことで順序付けが可能です。
例:{0;0;0} < {0;0;1} < {0;1;0} < {1;0;0}
Component内でのGH_Structureの扱い
Componentは、各入力Paramの
- GH_Structure
- データアクセス設定(詳細は後述)
- item:GH_Structure内のGooを1個ずつSolveInstanceに渡す
- list:GH_Structure内で1つのGH_Pathと対応しているGooのリストをSolveInstanceに渡す
- tree:GH_Structure自体をつSolveInstanceに渡す
をもとに、あるルールでどのような入力値の組み合わせ方でSolveInstanceメソッドを実行するかを決定し処理を行い結果を出力します。
ルールは以下です(データアクセスがtreeのケースは単純かつあまり無いのでitemとlistについて記述します)。説明の方法はいくつかあると思いますが、理解しやすく且つ誤解の生まれない説明を試みます。
⓪前提
- 各入力ParamのGH_Structureは、GH_PathをキーとしてGooのリスト(このGooのリストを以下便宜的にブランチと呼びます)を保持しており、それはGH_Pathにより昇順にソートされている
- 入力Paramごとにデータアクセス設定がitemまたはlistに設定されている
- 入力Paramはそれぞれ異なるブランチ数(=キーとなるGH_Path数)、ブランチ内のアイテム数を持っていてもよい
①各入力ParamのGH_Structureのブランチ同士の対応付けを行う
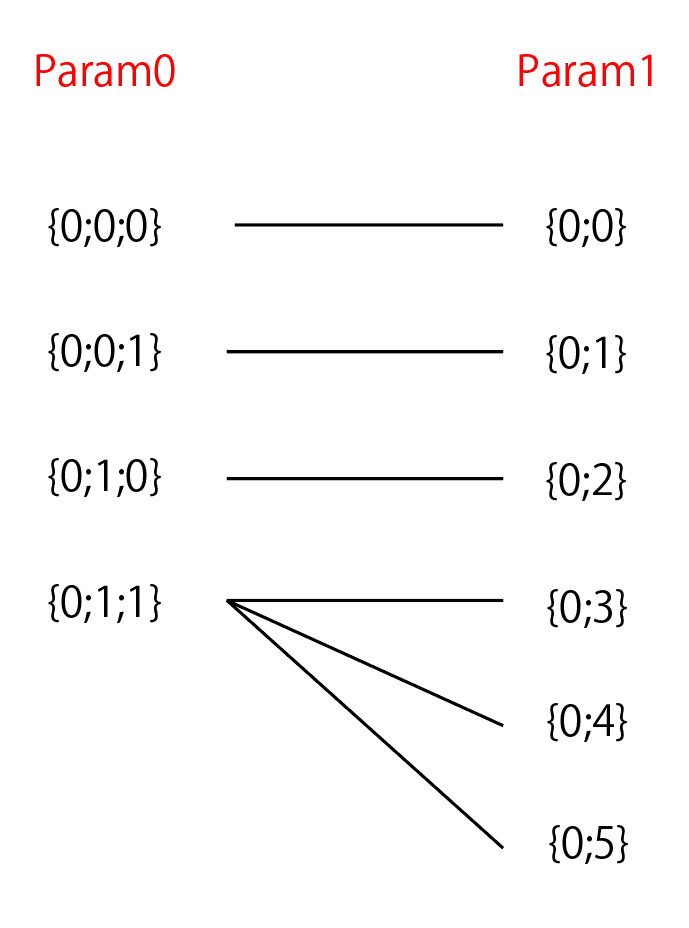
「それぞれのGH_Structureからn番目のブランチを取ってくる。ブランチ数がn個以下の場合は、末尾のブランチを取ってくる」というルールでGH_Structure間のブランチ同士の対応付けを行います。便宜的に以下ブランチセットと呼びます。
結果として、最もブランチ数が大きなGH_Structureのブランチ数分のブランチセットが定義されます。
②ブランチ内のGooを、SolveInstanceに渡す単位に分割する
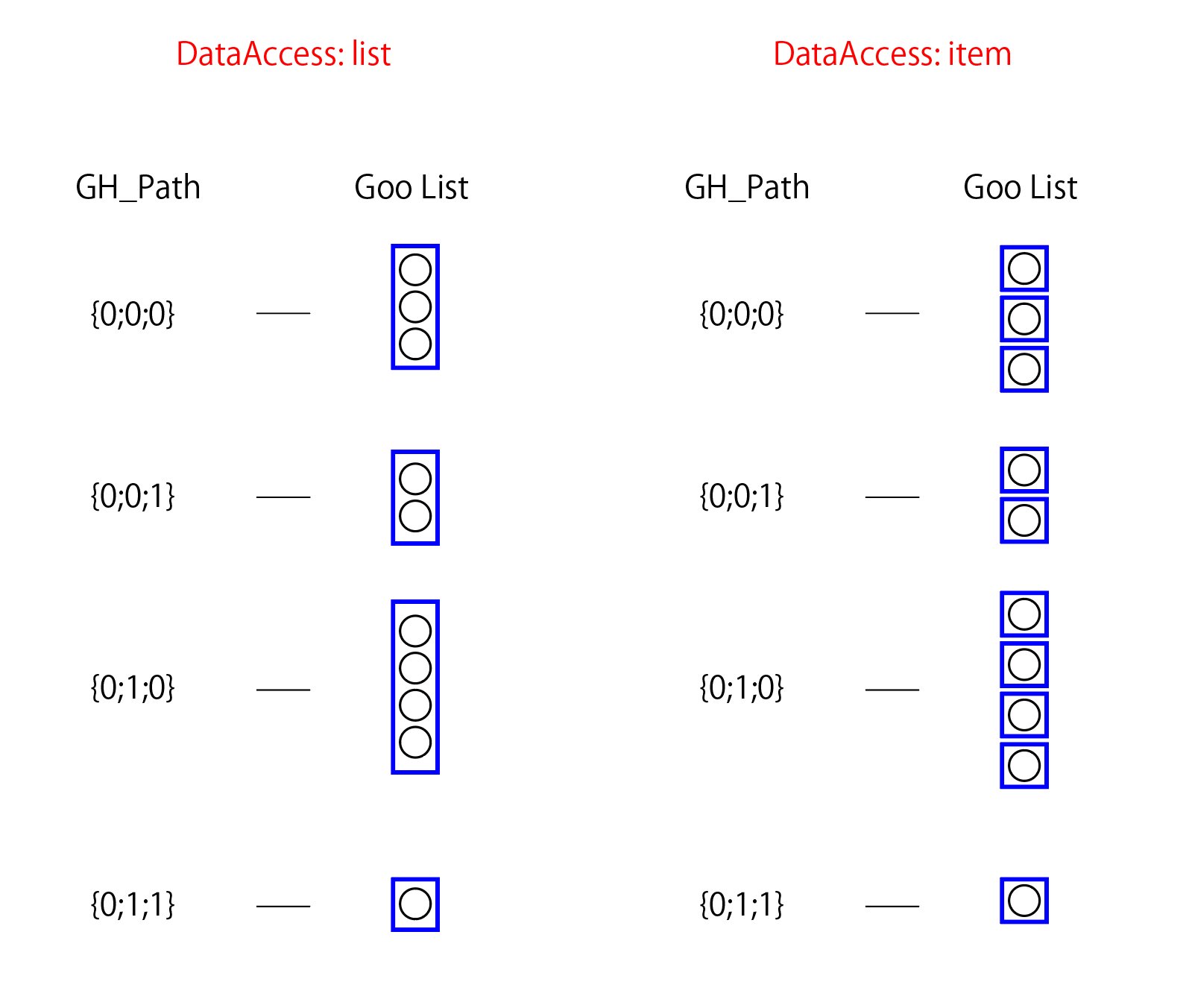
ブランチセット内の各ブランチに対して、「データアクセスがlistの場合はブランチ内の全Gooのリストを処理単位とする。データアクセスがitemの場合は、ブランチ内の各Gooを1個ずつ処理単位とする」というルールで処理の単位を定義します。
結果として、listの場合は1つの処理単位が出来ますが、itemの場合はブランチ内の要素数分の処理単位が出来ます。
③処理単位同士の対応をとる

ここまでで、ブランチセットが定義され、ブランチセット内の各ブランチに対して処理単位が定義されました。ここに対し、
「各ブランチからn番目の処理単位を取ってくる。ブランチ内の処理単位数がn個以下の場合、末尾の処理単位を取ってくる」
というルールで処理単位同士の対応を取ります。この組み合わせが晴れてSolveInstanceに渡される値の組み合わせとなります。
処理全体像の例
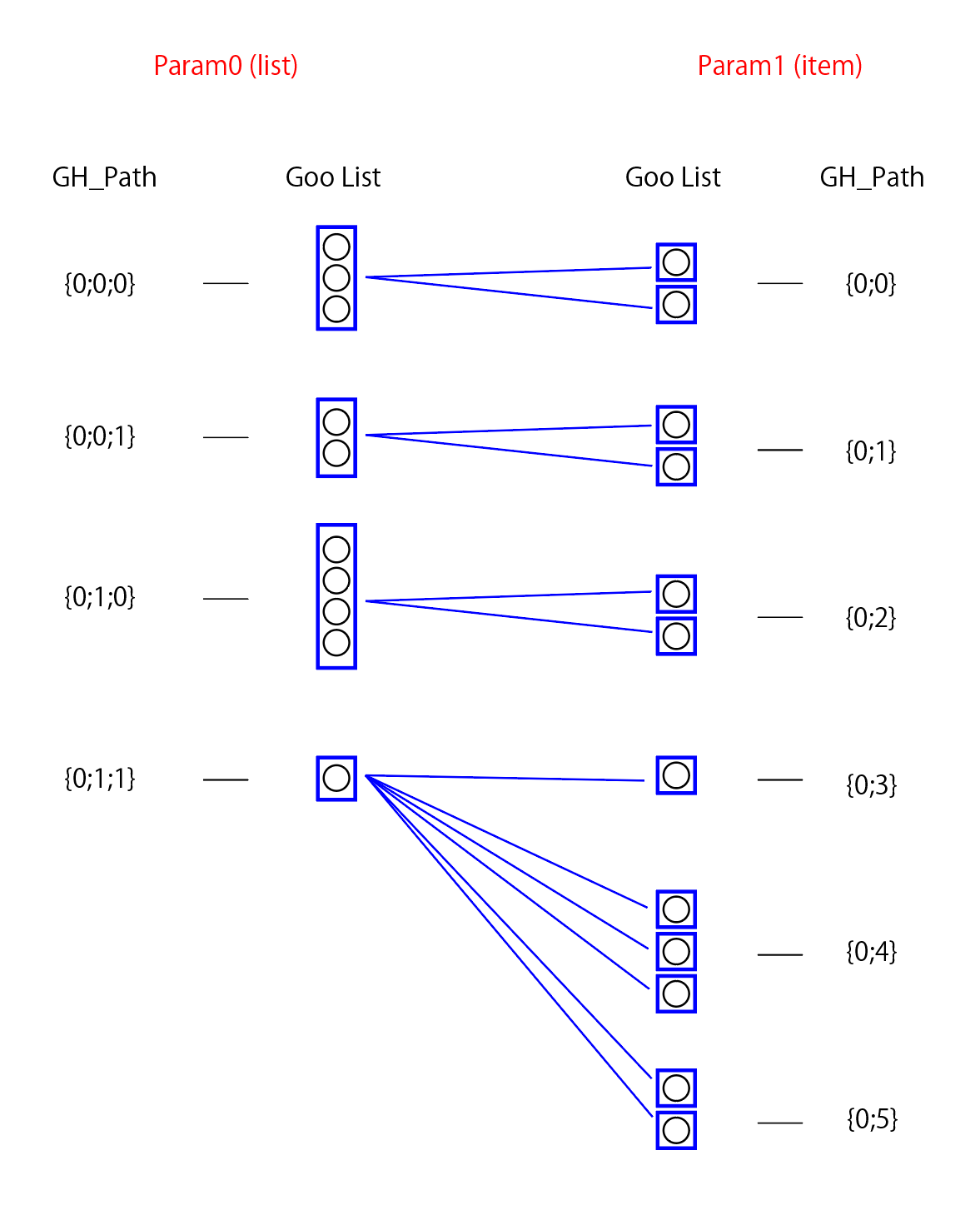
左右をつなぐ青線ごとにSolveInstanceが走り、結果が出力されます。
処理の対応関係にTree構造は関係ない
上記ルールを見て頂いて分かると思いますが、GH_Pathはあくまでブランチをソートするキーとして働いています。
整数の組みであるためツリー構造としての可視化や説明が公式含め多く行われていますが、例えば下のようなセットアップではツリー構造に準じた対応関係を期待してしまいますが、そうはなりません。
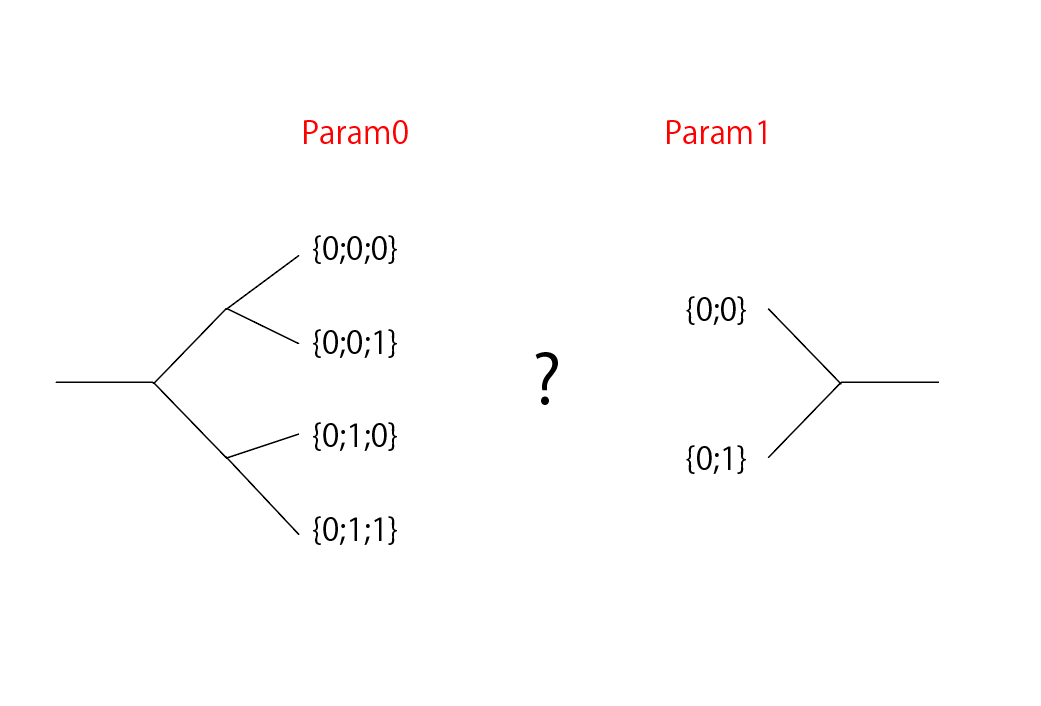
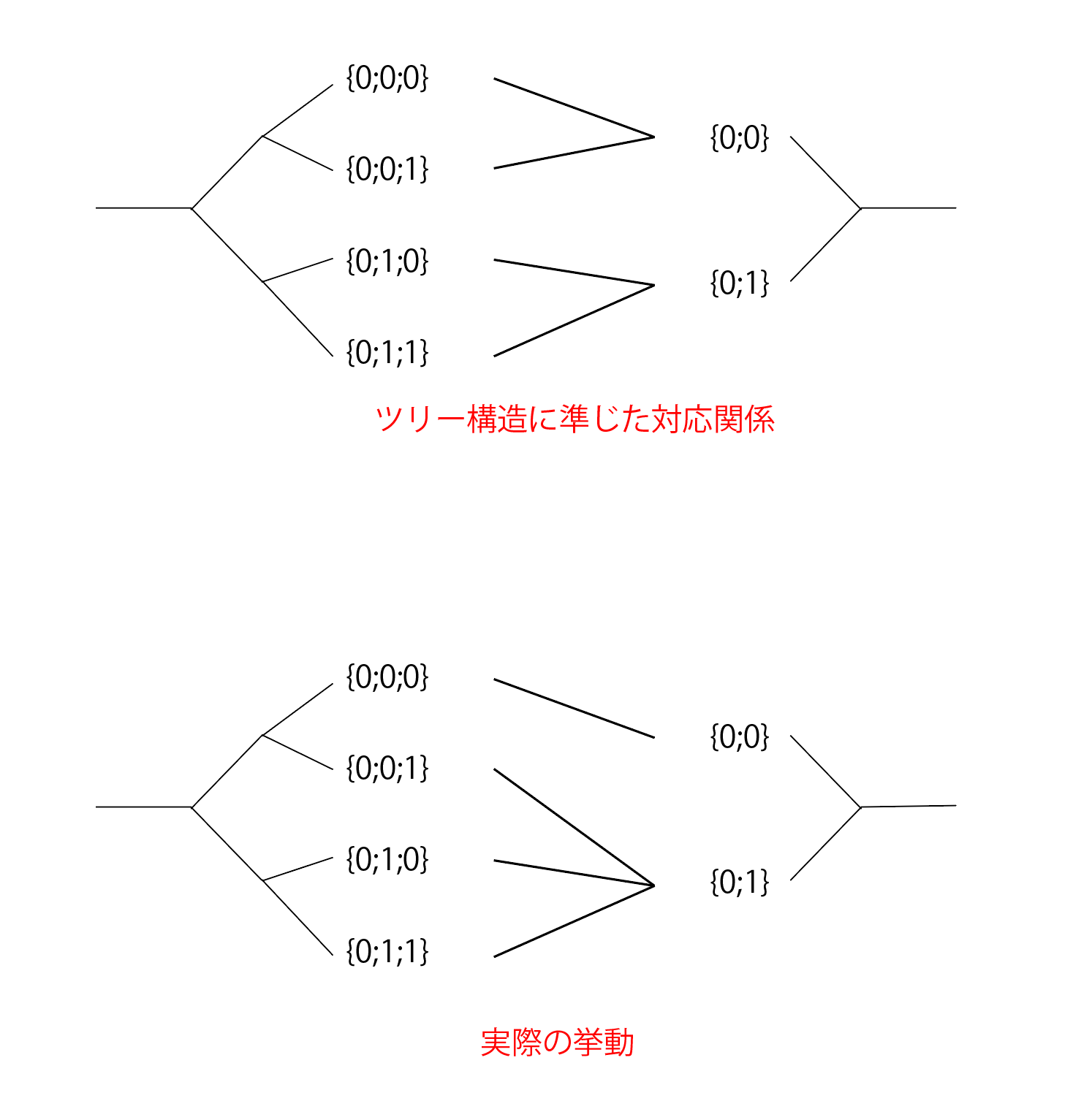
GH_Structureとの付き合い方
前述したような処理ルールを理解していれば、目的とする処理を実現するために必要なのは正しい構造のGH_Structureを作成したうえでコンポーネントに入力することのみです。
GrasshopperではデフォルトでGH_Structure操作のコンポーネントが多く提供されているほか、TreeSlothなど便利なアドオンも公開されています。
再帰処理を用いて定義されるアルゴリズムをGH_Structureのハンドリングで実現するのには慣れが必要ですが、慣れると各Paramのデータアクセス設定と入力するGH_Structure構造で多様な処理を実現することが出来ます。
次章以降で触れるC#でのComponent開発においては、コンポーネント内の処理ではもちろん如何様にも再帰処理が書けるのでご安心ください。
おすすめの学習コンテンツ
本章で触れたような原理さえ理解していれば、あとは習熟した方々のGrasshopperファイルや動画を見て写経するなどが効率的かと思います。
大量の素晴らしい動画やブログが公開されているのでコンテンツには困りません。
また、Rhinoと同様公式のForumとFood4Rhinoは必須です。
UIの見方から基本操作まで、ゼロからの入門に良いです
コンテンツが豊富です
自分が悩むことは大抵ここで一度は質問されています。英語で質問すれば強い方や開発者から即答されたりします
様々な資産が活発に共有されています。
丁寧かつ発展的な内容も含んでおり、何よりかっこよくてモチベーションの上がる例が多く載っている書籍です
さいごに
実装を始めるための前置きが長くなっていますが、本章では、Grasshopper周りの開発のために有用な知識の概説を行いました。この辺りの理解があるとGrasshopperの利用及びアドオン開発がよりスムーズになります。
次章では、本章で扱ったGoo,Paramの拡張を含めたGrasshopperアドオン開発について入っていければと思います。