概要
本技術ブログで、均質化の話題が何度か出ておりました。
(2)アディダス3DPシューズ解説:圧縮力をせん断変形に変換するメカニカルメタマテリアルの設計
本記事では弾性体と流体(流路)の観点で、数値実験によるラティス構造の均質化方法と結果の可視化について紹介します。
本記事は後編で、流体(流路)の均質化について紹介します。
前編はこちら:(1)ラティス構造の均質化
なお、本記事ではAdditive Manufacturing前提となるようなラティスの均質化を紹介しておりますが、
クライアントワークにおいては、メタマテリアル構造設計技術を活用しつつ顧客の製造設備で量産可能な設計開発の支援を行うことが一般的です。
数値実験による流路の均質化
流路の均質化手法として多孔質モデルが一般的に知られています。
多孔質モデルを用いて周期的な流路を均質化する過程を紹介します。
定式化
多孔質体内部の流れにおける流速\boldsymbol{v}はダルシーの法則(Darcy's law)により表現され、低レイノルズ数において圧力勾配に比例し粘性係数\muに反比例することが知られています。
\begin{align*}
{\boldsymbol{v}}=-\frac{\kappa}{\mu}\boldsymbol{\nabla}p
\end{align*}また、ダルシーの法則に慣性の寄与を加えて、圧力損失を速度に比例する粘性項と速度の二乗に比例する慣性項の和で表現したDarcy-Forchheimer equationもあります。
\begin{align*}
\nabla p=-\frac{\mu}{\kappa}v-\frac{\rho}{\kappa'}v^2
\end{align*}多孔質モデルではこれら速度と圧力勾配の関係式をそのまま支配方程式としたり、ナビエ-ストークス方程式の圧力ソース項に入れたりします。
今回は周期的な流路の圧力損失(圧力勾配)を、以下のようにナビエストークス方程式の圧力ソースに入れて定式化します。
\begin{align*}
(\boldsymbol{v}\cdot\nabla) \boldsymbol{v}
=-\boldsymbol{\nabla} p - \mu\Delta \boldsymbol{v} - \mathbf{\alpha}\boldsymbol{v} - \beta|\boldsymbol{v}|\boldsymbol{v}
\end{align*}\alphaと\betaはは多孔質モデルの行列パラメータで、簡単のため定常非圧縮の流れを考えています。
数値実験による多孔質モデルのフィッティング
2次元のラティスを例に均質化過程を紹介します。
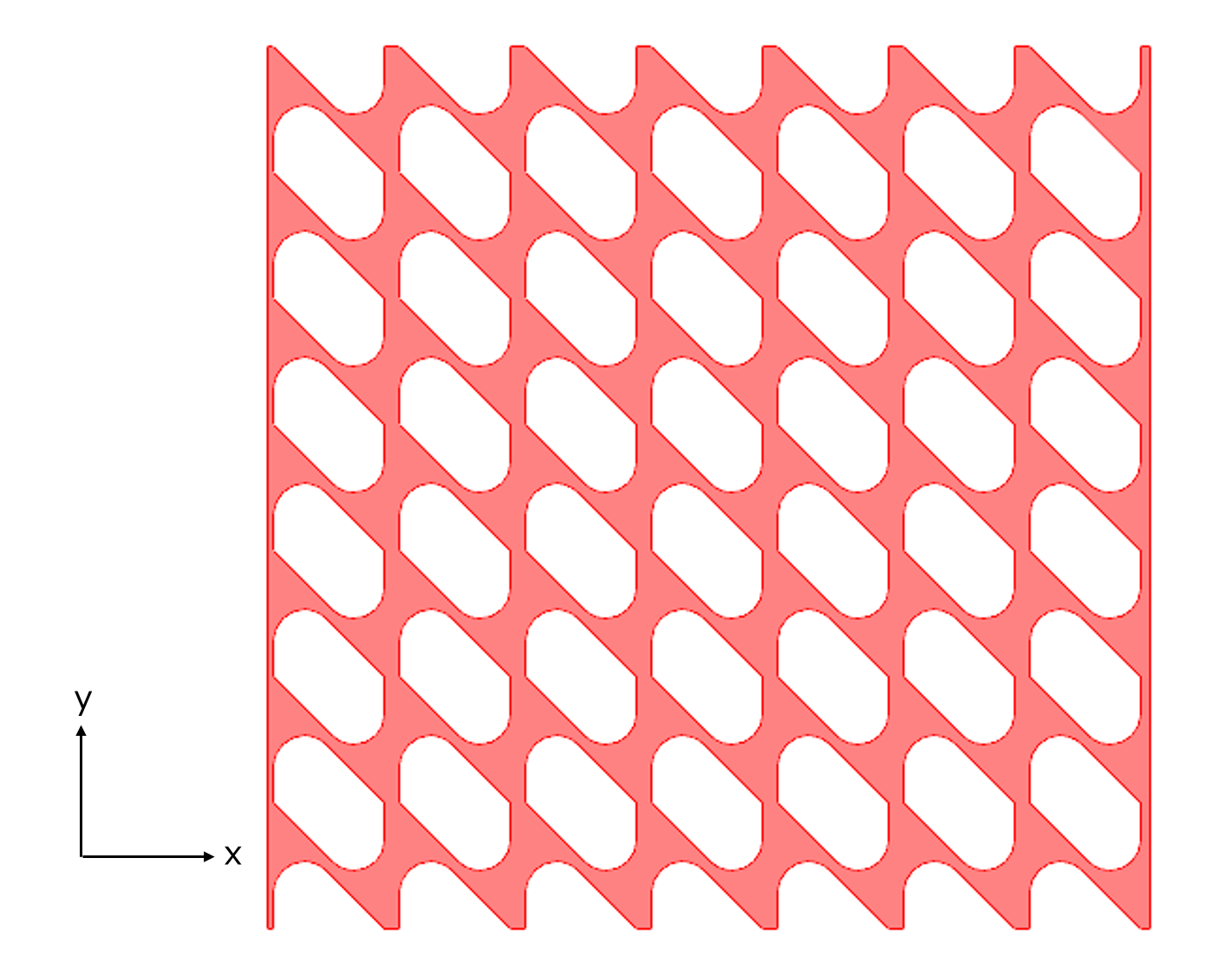
単位構造を取り出すと以下のようになります。

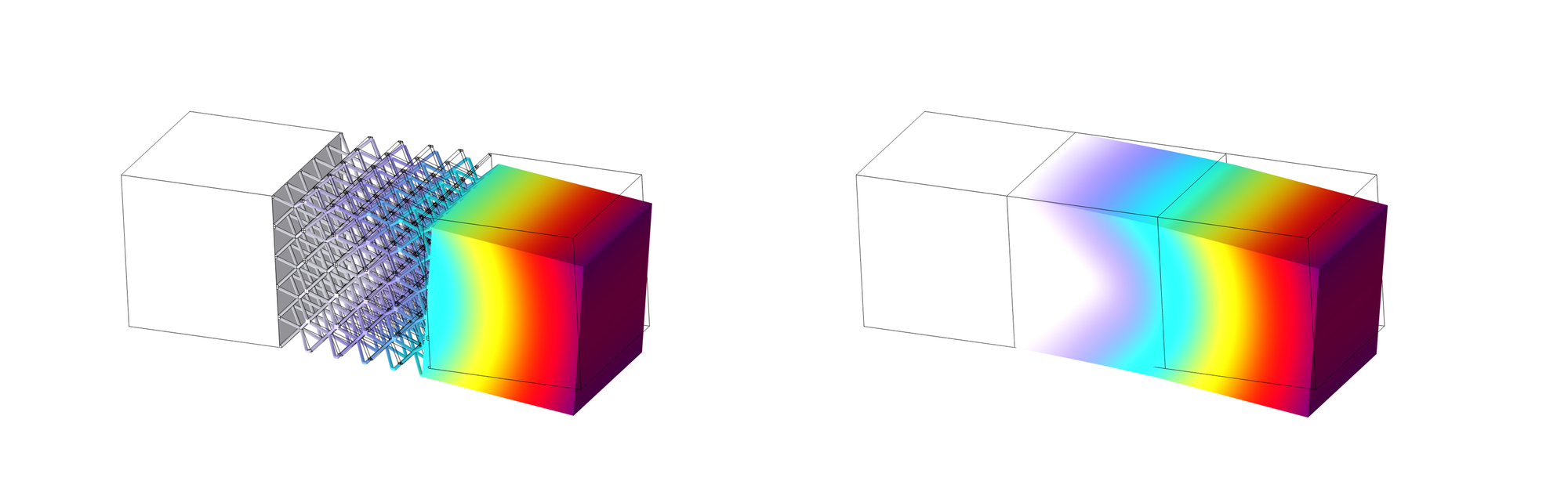
この単位構造の境界速度の周期境界を設定したうえで、下図のように各方向に圧力勾配を加え解析します。
解析した結果をいくつか図示します。
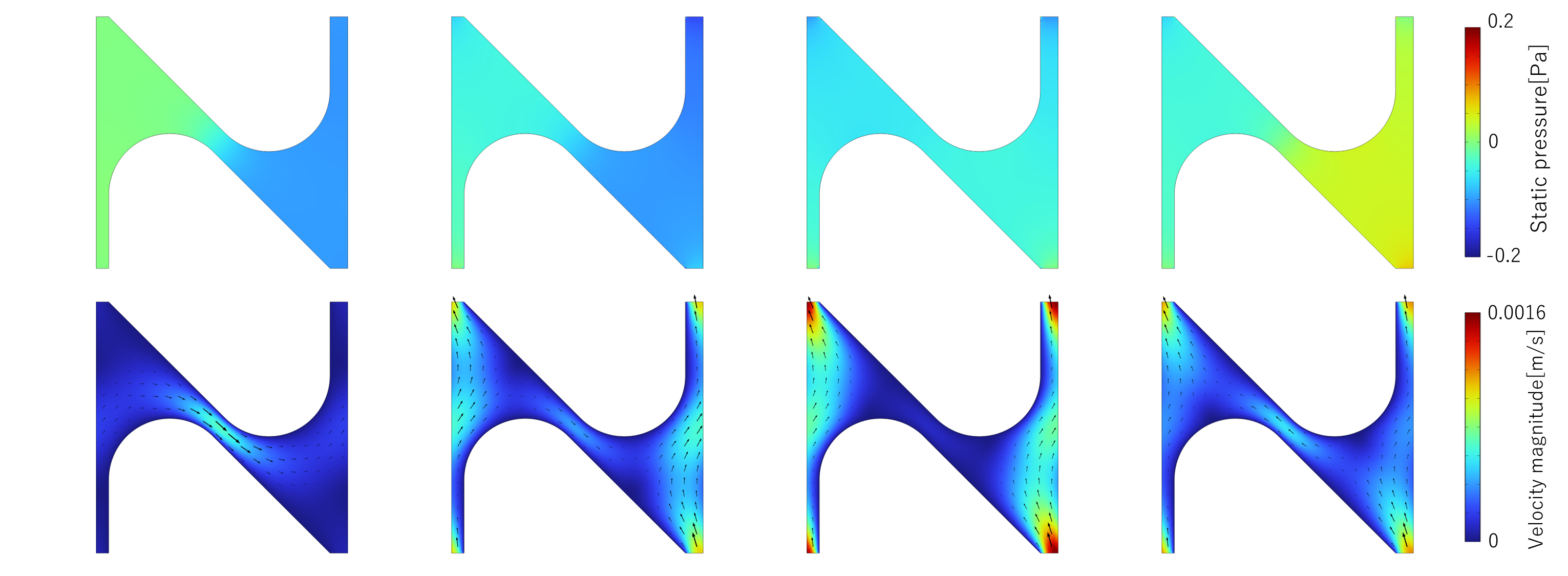
このように各方向の圧力勾配に対して速度場が得られます。
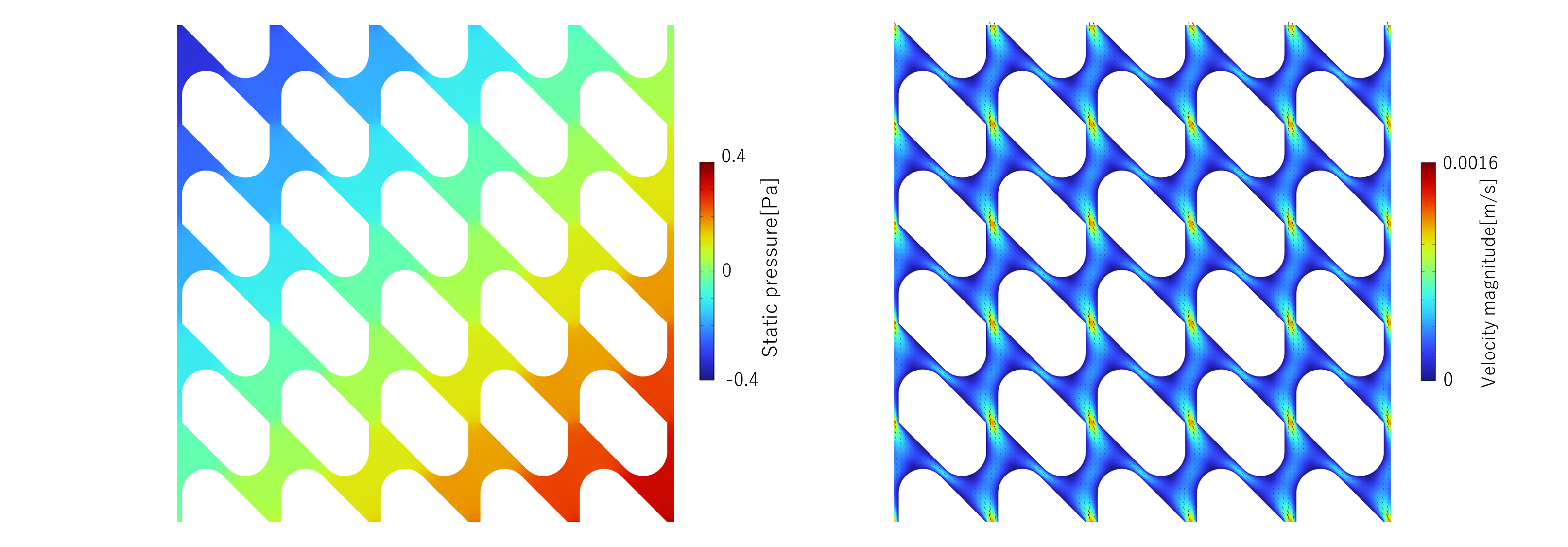
ここでは単位構造の解析をし結果を可視化しましたが、周期境界条件用いているため流路が周期的に繰り返した状況での解析となっています。
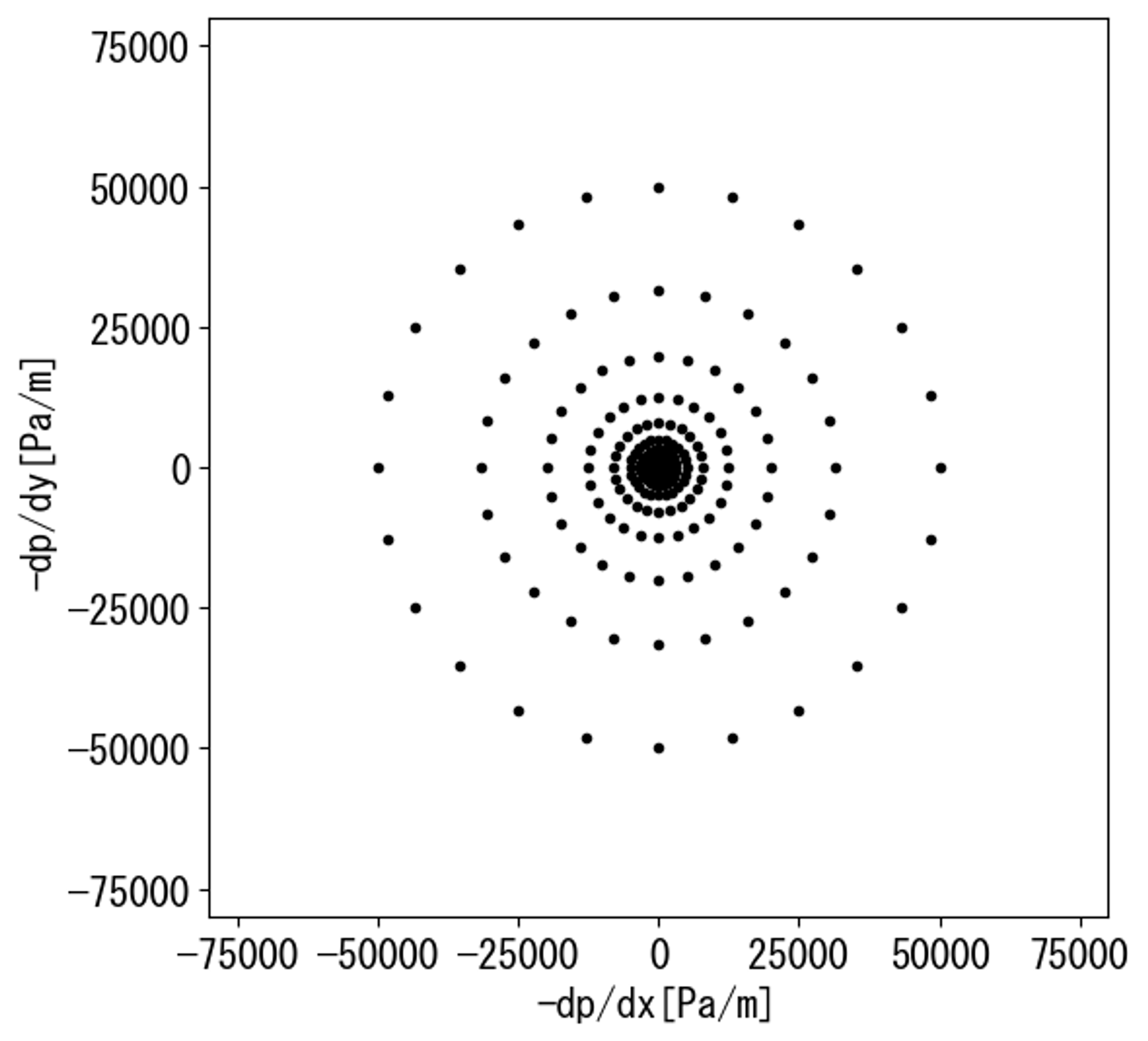
各圧力勾配の解析結果において、非流路部分も含めて速度の平均をとり見かけ速度を見積もります。
入力した圧力勾配とともに、解析結果から得られた見かけ速度を赤矢印の向きと大きさでマッピングすると以下のようになります。
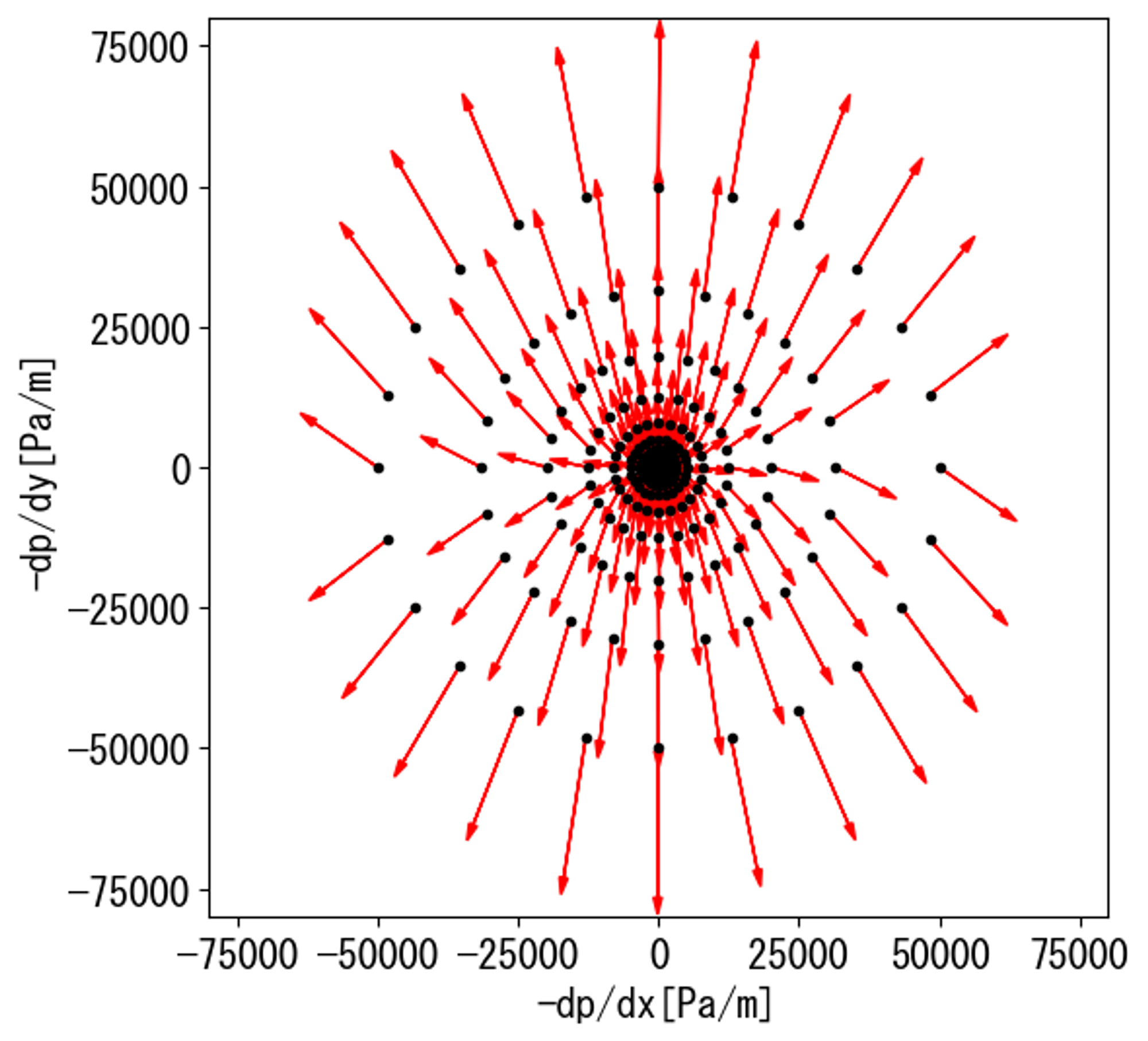
この数値解析で得られた圧力勾配と見かけ速度の結果から、多孔質モデルの行列パラメータ\alphaと\betaを算出します。
定式化においてナビエストークス方程式の圧力ソース項に周期流路による圧力損失を入れ込むと説明しましたが、均質化した周期流路による圧力ソースはナビエストークス方程式における粘性項および慣性項より十分大きくなるという考えのもと、均質化のうえではDarcy-Forchheimer equation相当の式でフィッティングをします。
\begin{align*}
\boldsymbol{\nabla} p = - \mathbf{\alpha}\boldsymbol{v} - \beta|\boldsymbol{v}|\boldsymbol{v}
\end{align*}まずは圧力勾配の大きさが500Pa/m以下のデータのみを使用してフィッティングしてみます。
解析結果をもとに見かけの速度を入力、圧力損失を予測する値として線形回帰で\alphaと\betaを算出したうえで、"解析の入力圧力損失"と"速度から推定される圧力損失"および"入力圧力損失と推定圧力損失の誤差"をプロットすると以下のようになります。
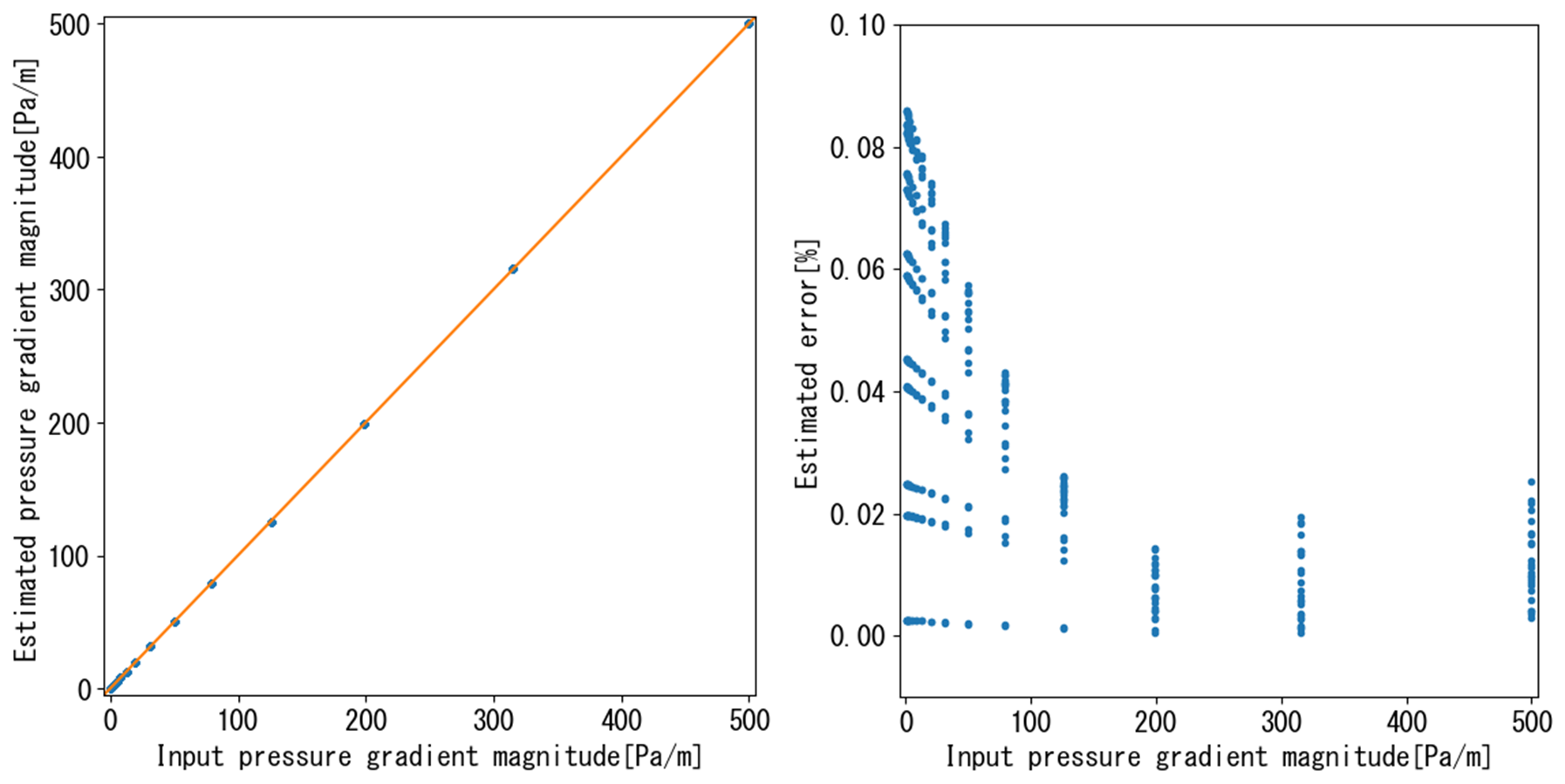
圧力損失が小さく速度が遅い(レイノルズ数が小さい)ときは、ある程度精度よく多孔質モデルにより流れをフィッティングすることができました。
次に、すべてのデータを使用してフィッティングしてみます。
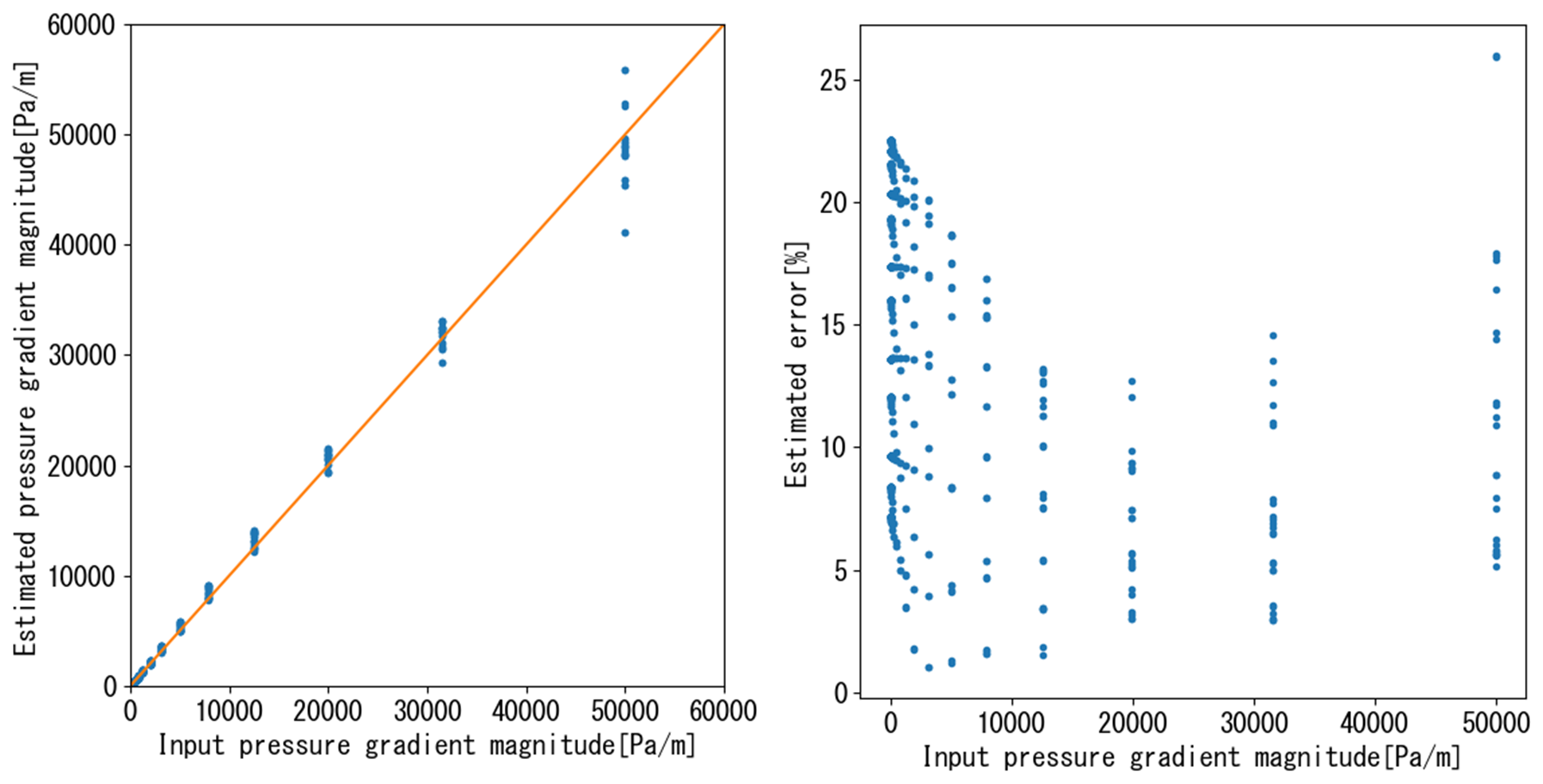
最大で30%近く誤差が出ており、あまり精度よくフィッティングができていません。
圧力勾配が大きいと速度およびレイノルズ数が大きくなり相対的に慣性の寄与が大きくなります。
今回均質化しているラティス構造は慣性により大きく流れの形態が変わりえて、慣性の寄与度に異方性があります。
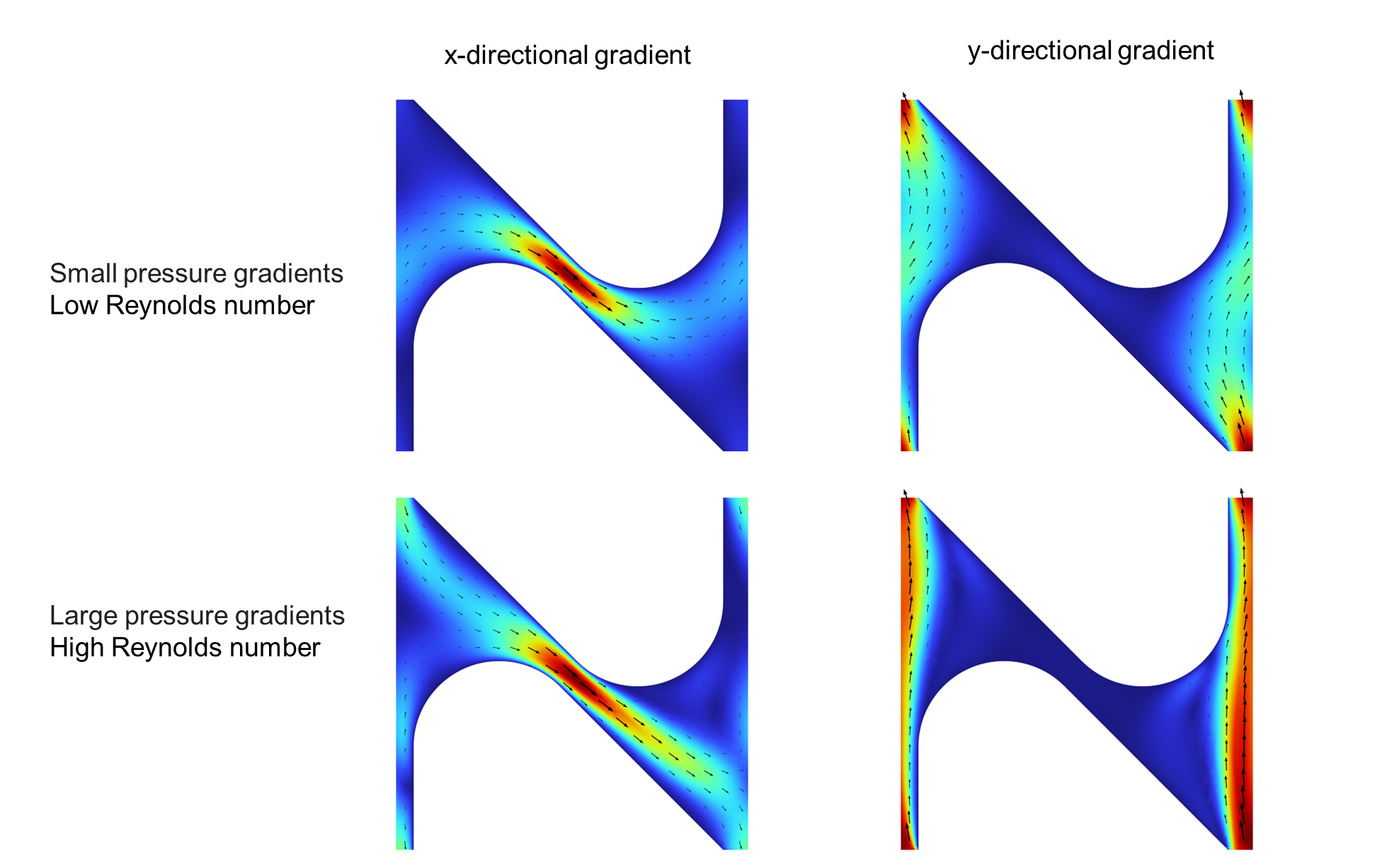
そのため、今回の多孔質モデルの定式化の範囲では流れを表現しきれず誤差が大きくなったと考えられます。
実際に均質化を行う場合は、扱う均質化のモデルが適用できる範囲を注意する必要があります。
多孔質モデルによる解析
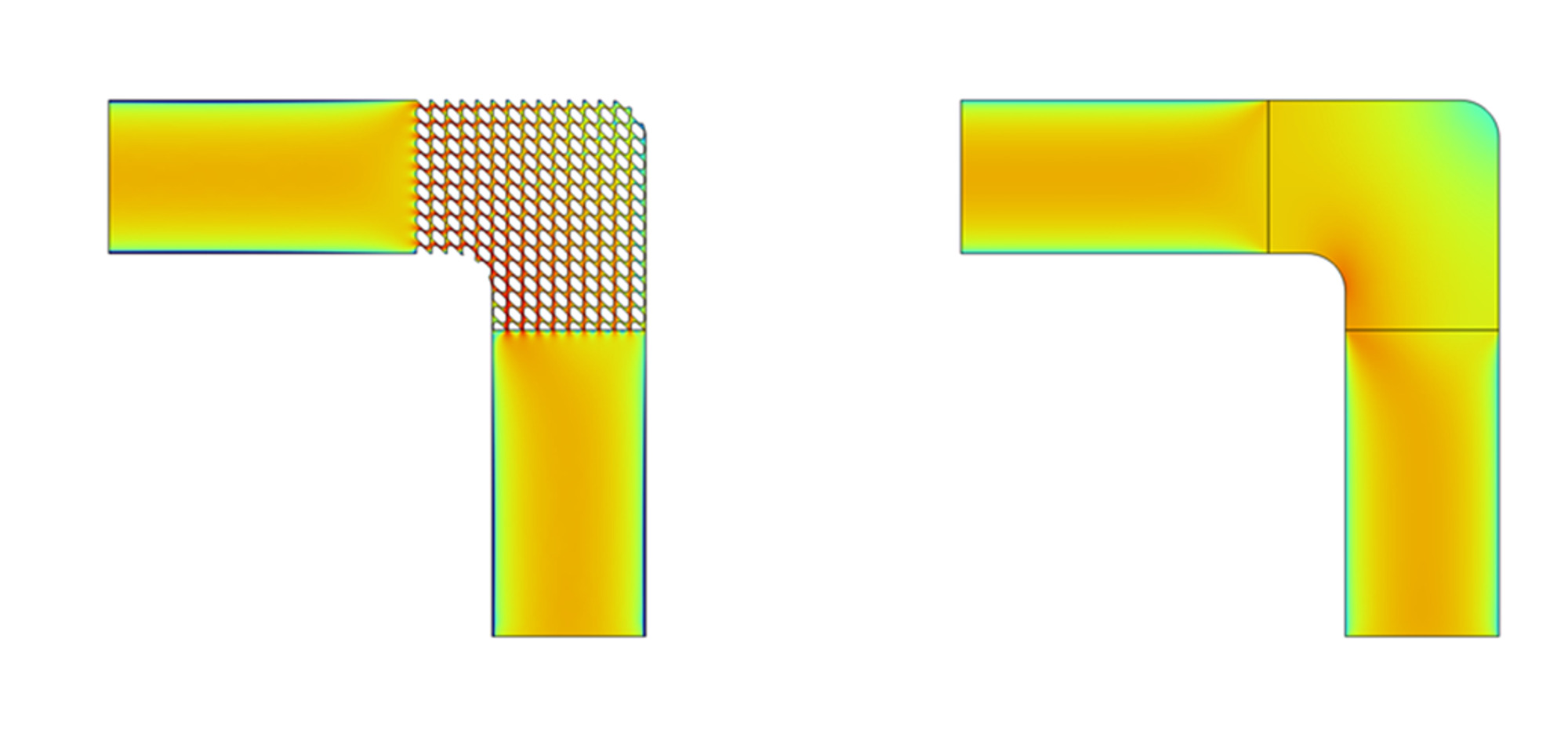
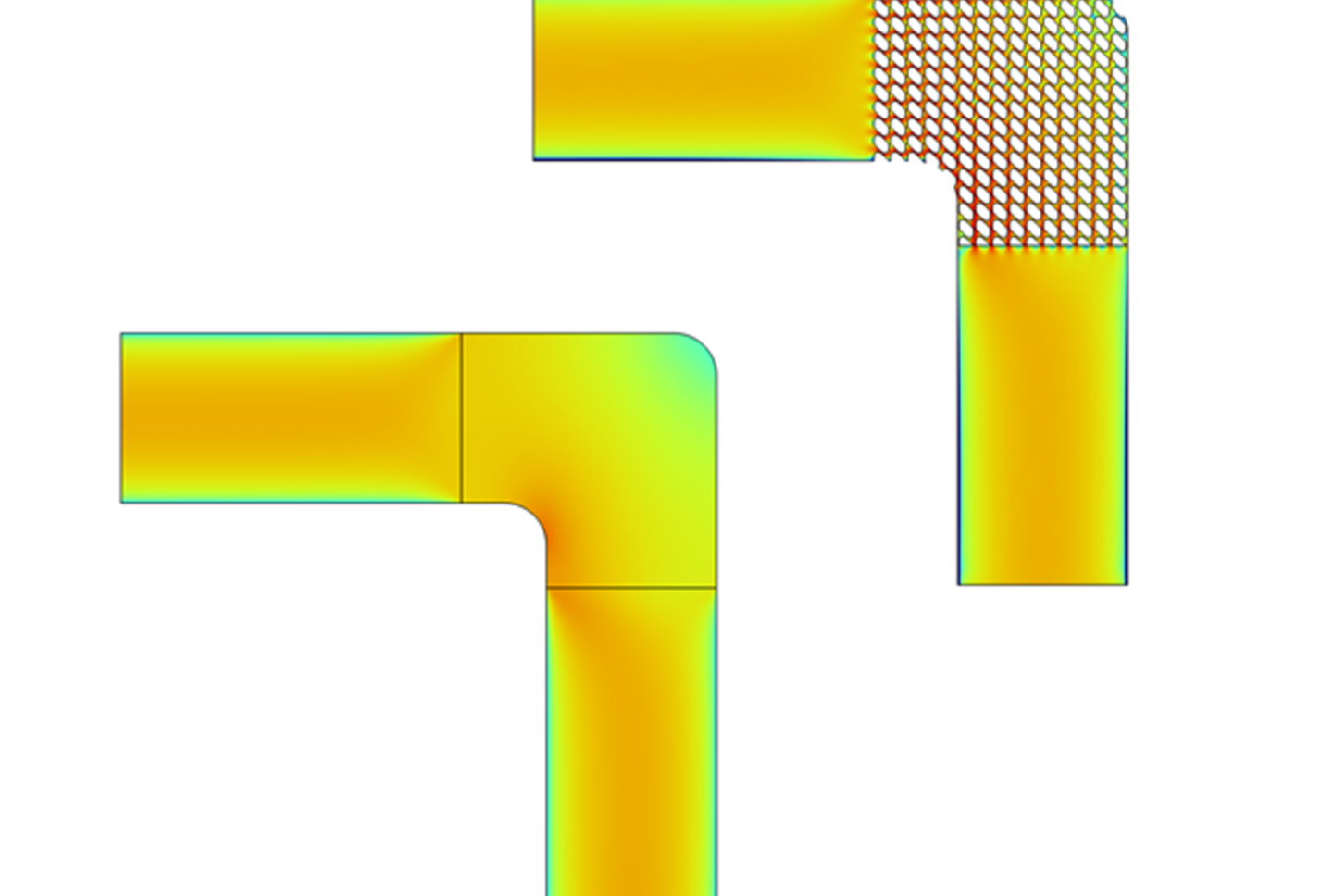
圧力損失500Pa/m以下のデータ使ってフィッティングした多孔質モデルにより、以下の3つの流路の解析を行います。
1,2番目の流路はラティス構造の向きが異なっています。
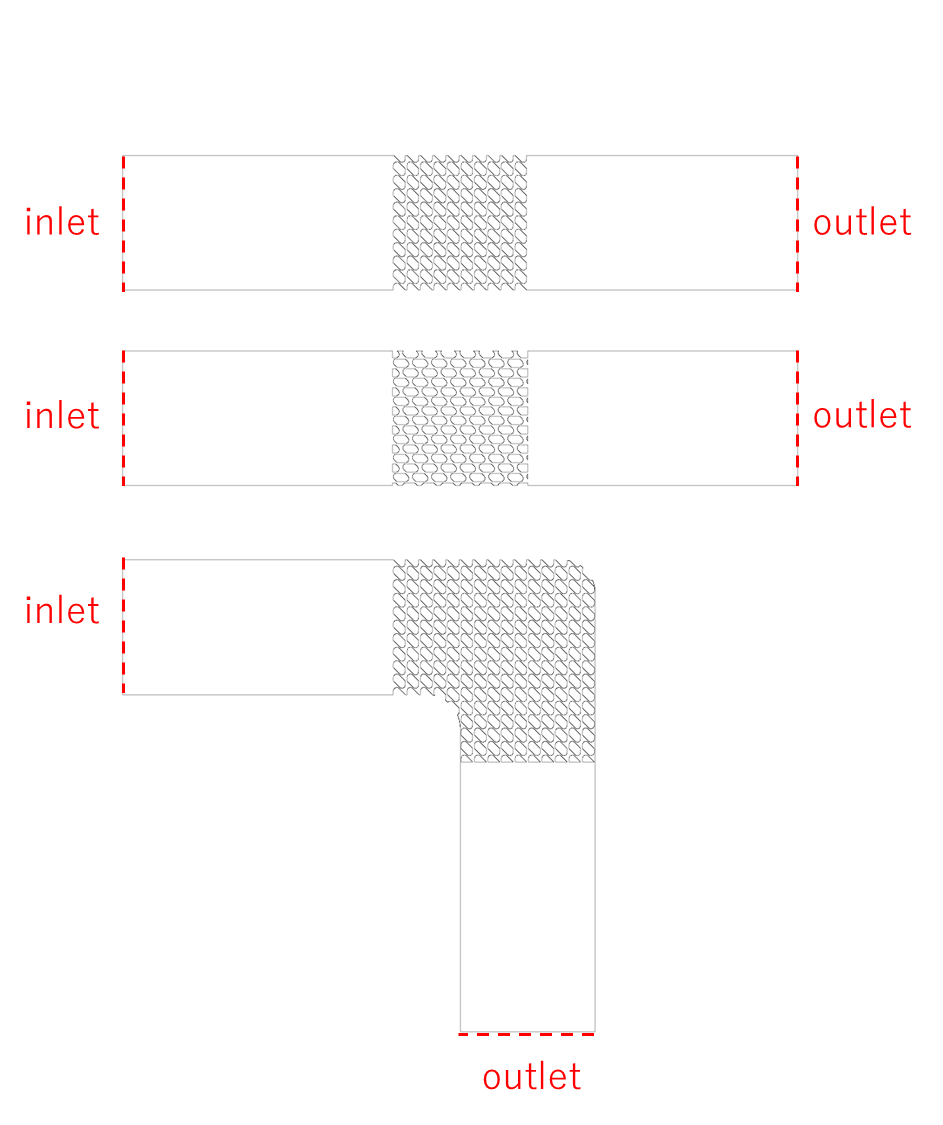
流入口と流出口の圧力差を一定にして解析して、均質化していないものとしたものを比較した結果が以下になります。
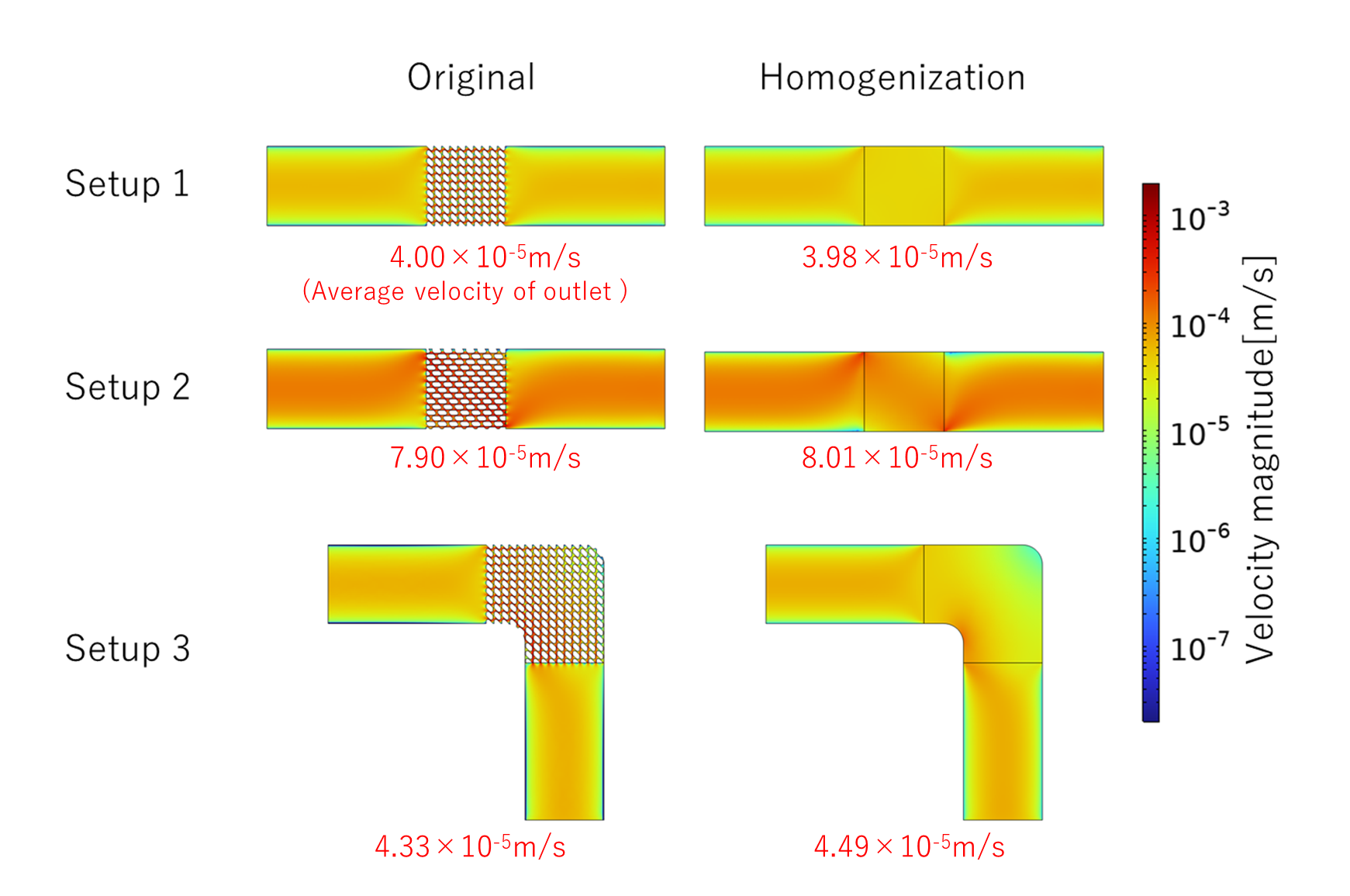
単位構造の繰り返し回数が少ないこともあり多少の差はありますが、多孔質モデルで流れを再現できていることがわかります。
ラティス構造の各方向の流れやすさ可視化
本記事の前編で均質化した弾性行列の可視化を行いました。
同様の可視化手法を用いて、十分流れが遅い状況におけるラティス構造の各方向の流れやすさの可視化を行ってみます。
下図のように、各流れの方向に2次元または3次元の空間上で原点からそれぞれの方向に圧力損失に対応する距離だけ離れた点で表現します。
それらの点を結んで線または面にすることで、各方向の流れやすさを可視化します。
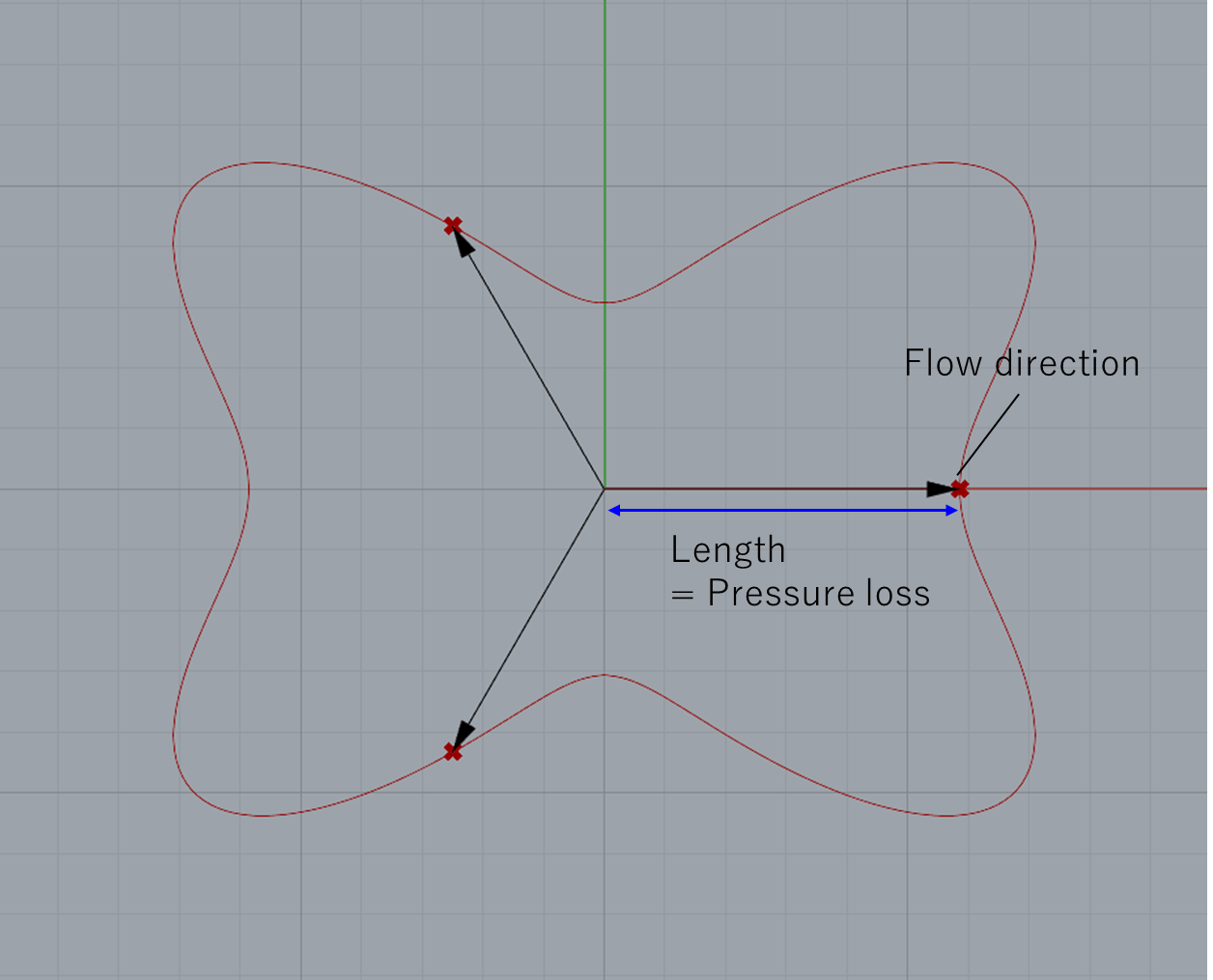
以下でいくつかのラティスについて各方向の流れやすさを可視化します。
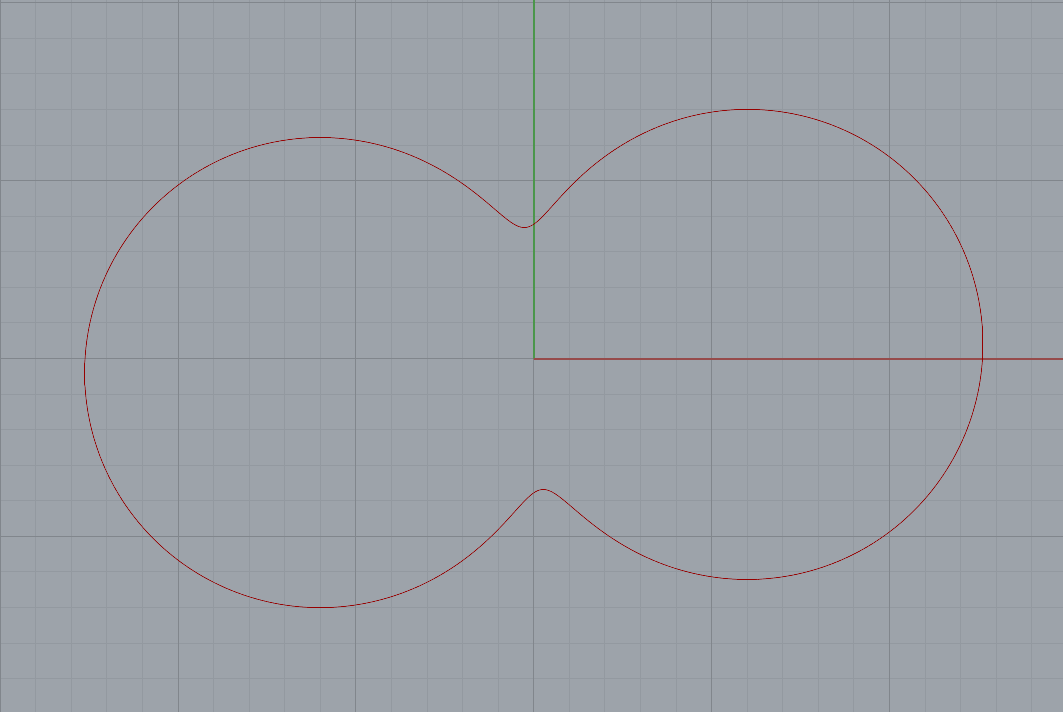
2次元ラティス
上記で均質化した2次元ラティスを均質化します。

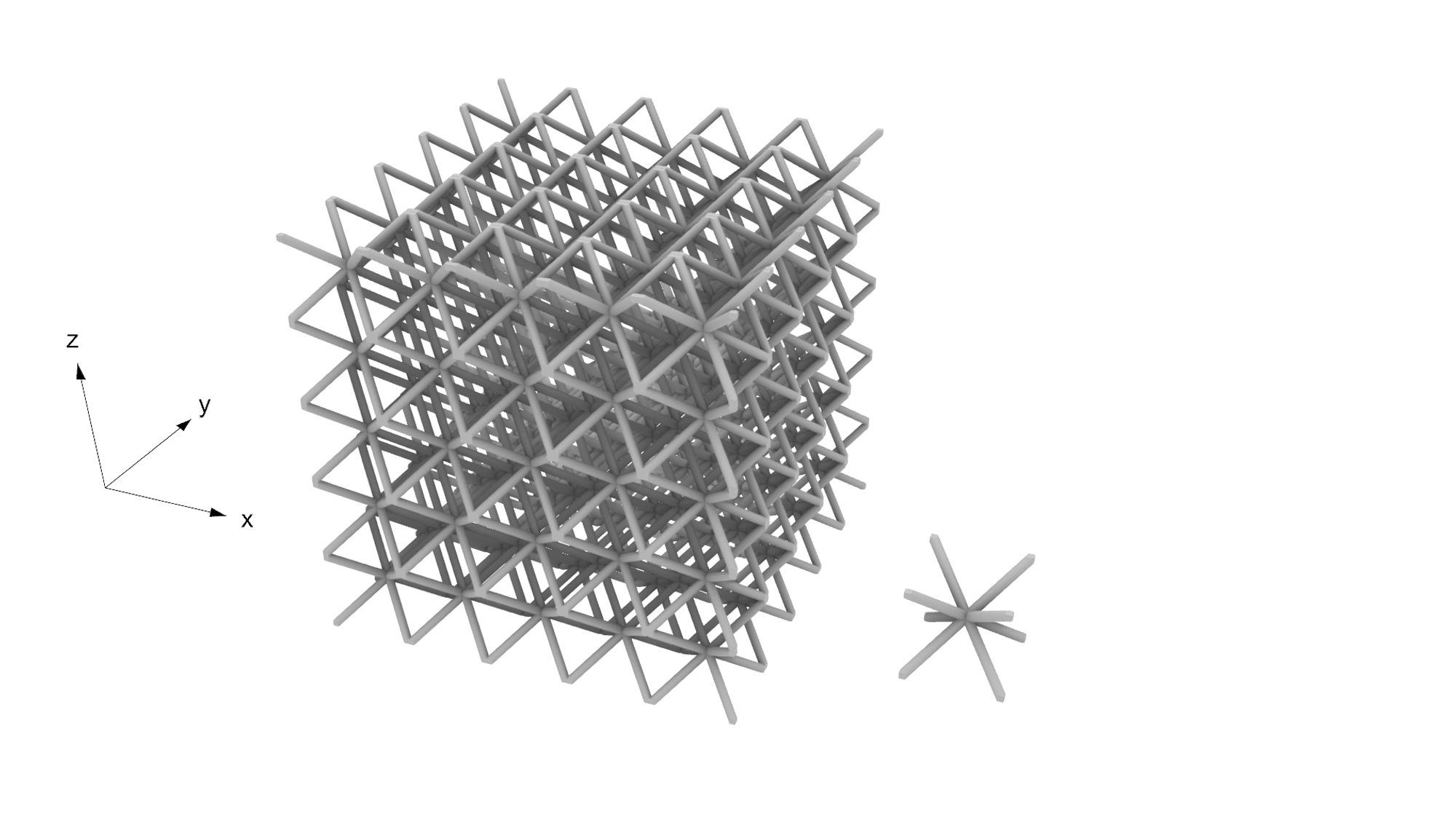
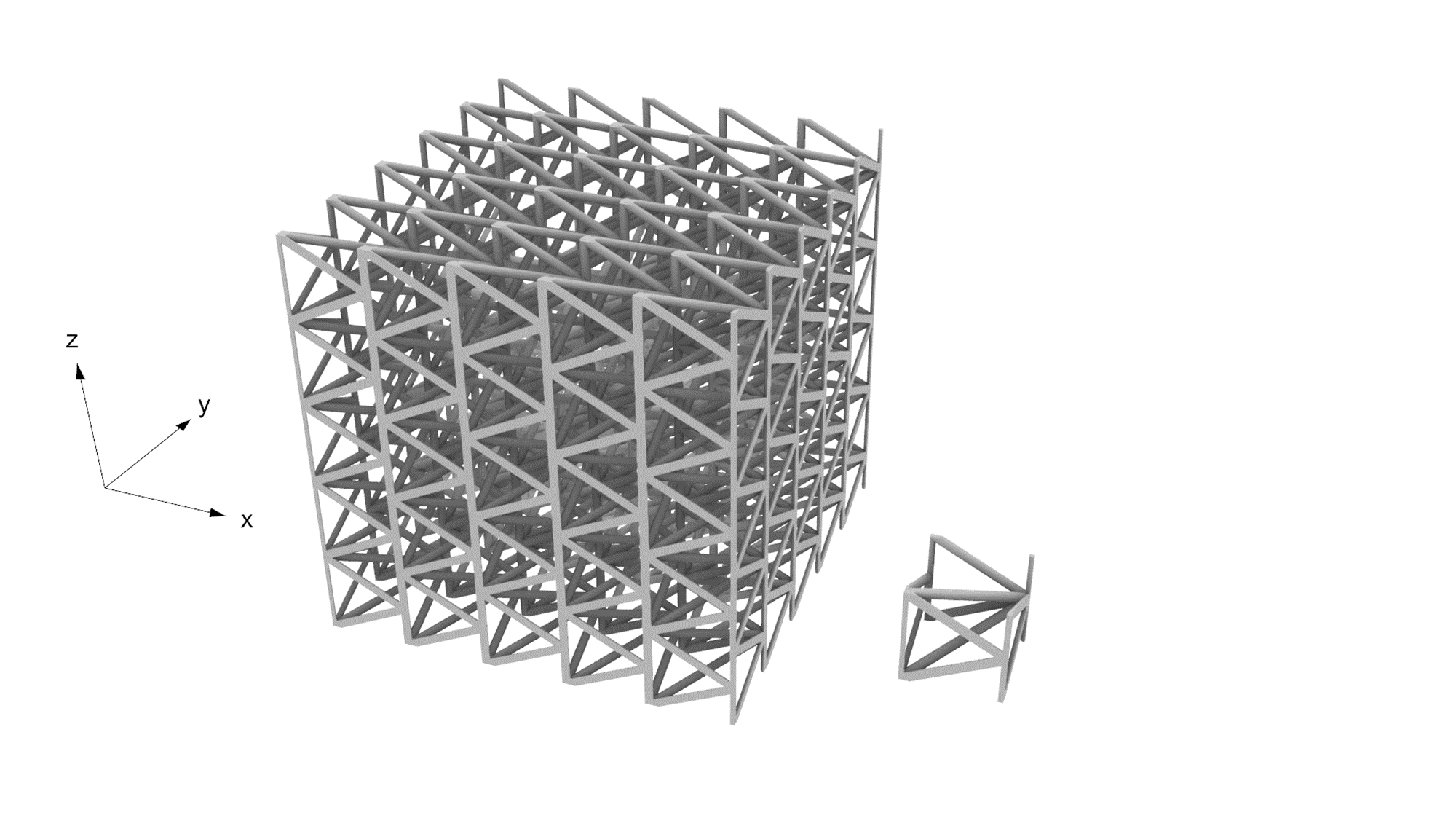
3次元ラティス1
下図1枚目は流路の壁面を、2枚目は解析結果の一例を、3枚目は各方向の流れやすさのを図示しています。

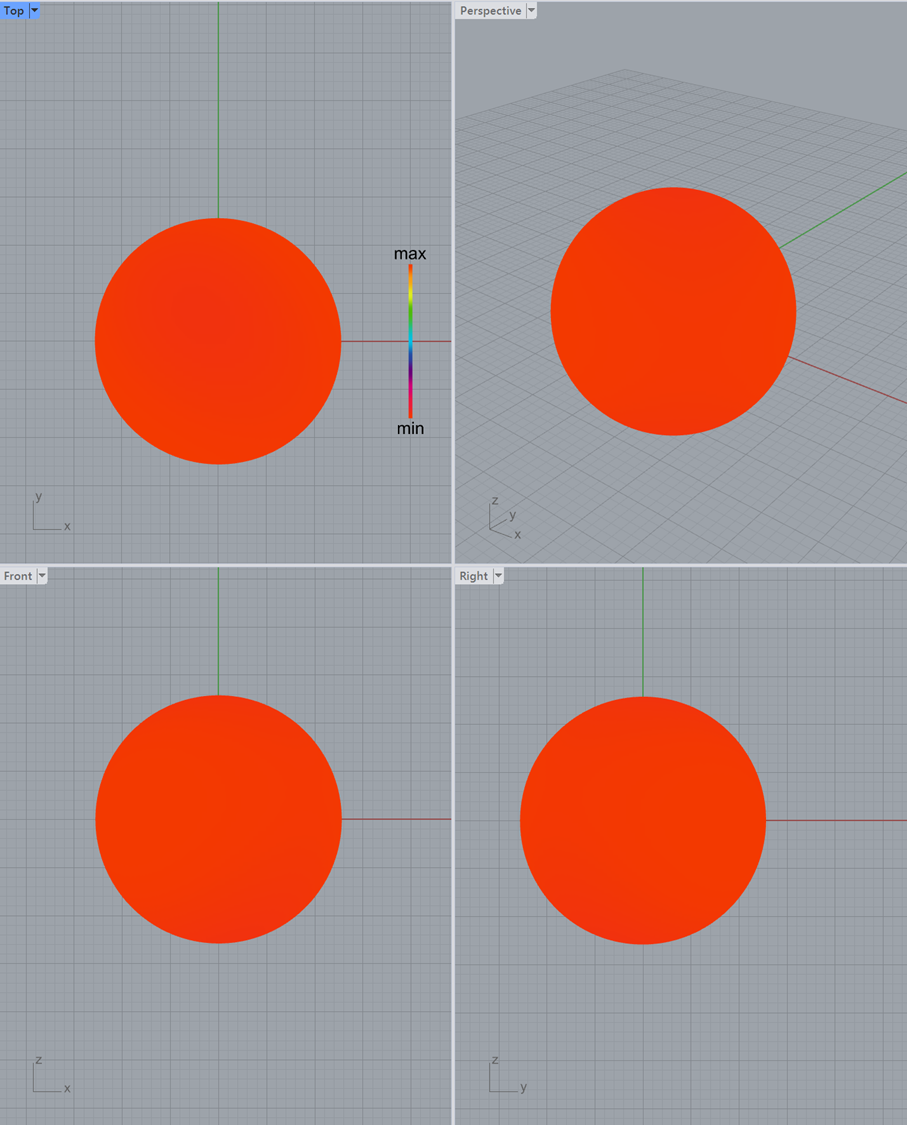
3次元ラティス2
3次元ラティス1と同様に、流路の壁面と各方向の流れやすさを図示しています。

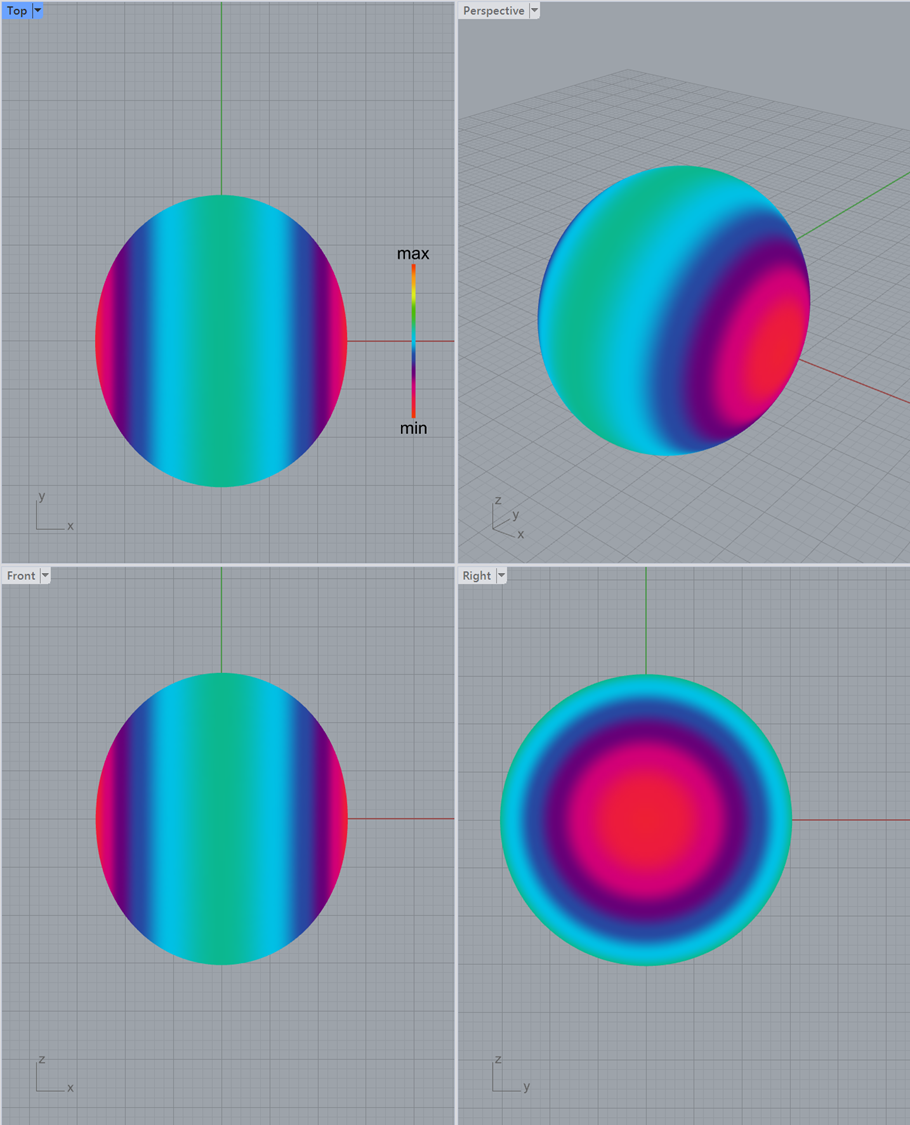
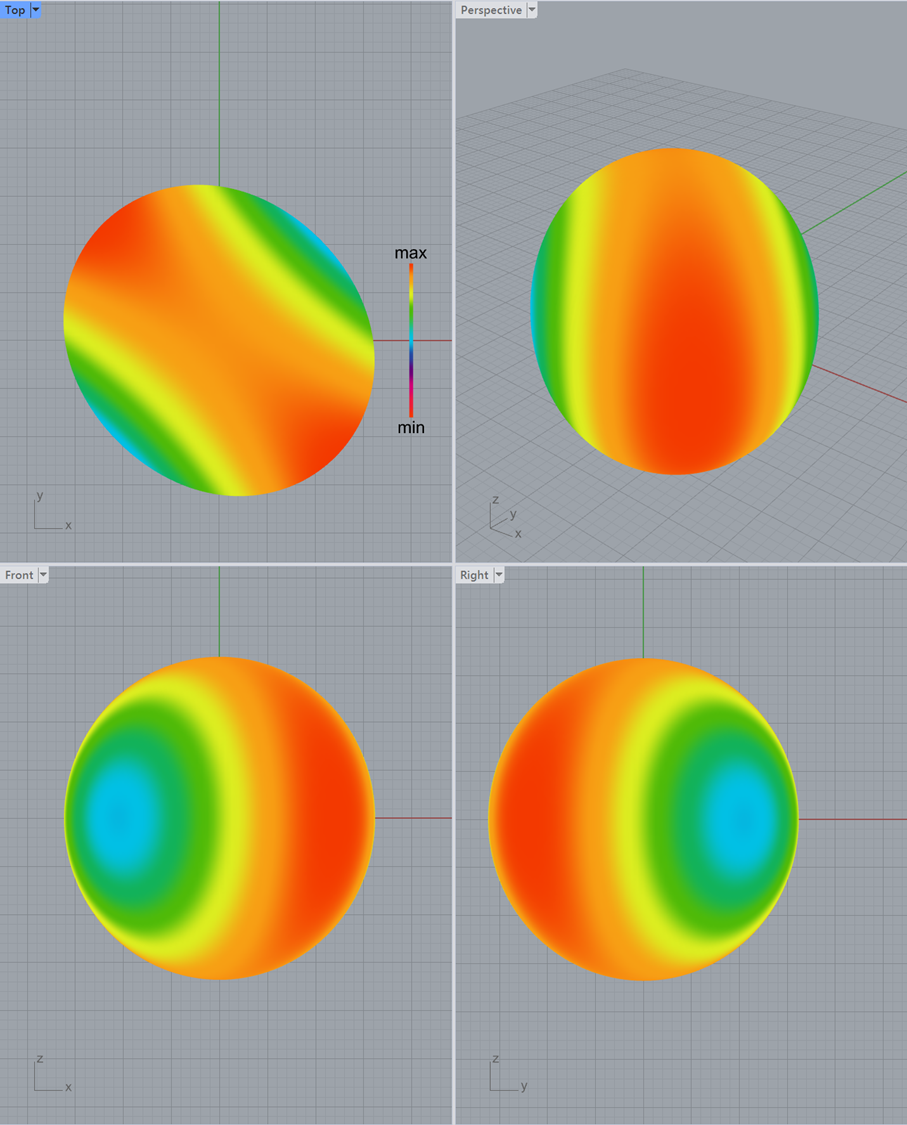
3次元ラティス3
3次元ラティス1,2と同様に、流路の壁面と各方向の流れやすさを図示しています。
最後に
本記事は、前編で構造の弾性行列による均質化と弾性行列の可視化方法について、流路の多孔質モデルによる均質化と各方向の流れやすさの可視化について紹介しました。
均質化は様々な分野で使われ、計算コストを下げるだけでなく、現象の理解にも役立ちます。
興味を持った方はぜひ均質化をやってみて下さい!