はじめに
Nature Architects では、メタマテリアルを活用した製品設計アルゴリズムを開発しています。私たちはこれらをデリバリーやコスト、品質の観点で現実的に量産可能なものにすることを目指しています。
本報では「折りたたみハンガー」を事例に、生産設計の進め方について解説します。「折りたたみハンガー」においては、コンプライアントメカニズムを応用した新しい構造・機能について提案しました。私たちは第1部で解説した機能設計と同時並行で生産設計を進めました。
第2部では、提案した機能を既存の量産技術、ここではプラスチックの射出成形で実現するための設計について、基本的な手順を示します。
材料、条件、用語など
解析ツール:
材料材料
- POM、Duracon M90-44(Polyplatics)
- 熱伝導率
k : 0.24 W/mK
- 比熱
c_p : 2,000 J/kg K
- 密度
\rho : 1,300 kg/m^3 (溶融時)
- 取出可能温度
T_e : 143 ^\circ C
成形条件
- 溶融温度
T_i : 200 ℃
- 金型温度
T_d : 80 ℃
- 射出率
Q : 50 cm^3/s
- 充填時間
t_f : 1s
- VP切替 : 自動計算(Moldflow)
- 保圧力
P_h : 充填圧力の80%
- 保圧時間
t_h : 10s
- 冷却時間
t_c : 自動計算 (Moldflow)
射出成形機
- 最大射出圧力
P_{max} : 180 MPa
- 最大型締め力
F_{max} : 7,000 ton
実用性の概略検討
実用的な量産工法として射出成形を用いることにします。まず最初に、コストを意識しながら加工の可否を検討します。この段階は次の3項目についての大まかな確認であり、この段階を経て設計変更したもので詳細検討を行います。
- 溶融プラスチックは金型内に充填できるか?
- 製品の厚みは適切か?
- 製品は金型から抜くことができるか?
第1部で解説した折りたたみ構造について、その初期形状、寸法を下図に示します。
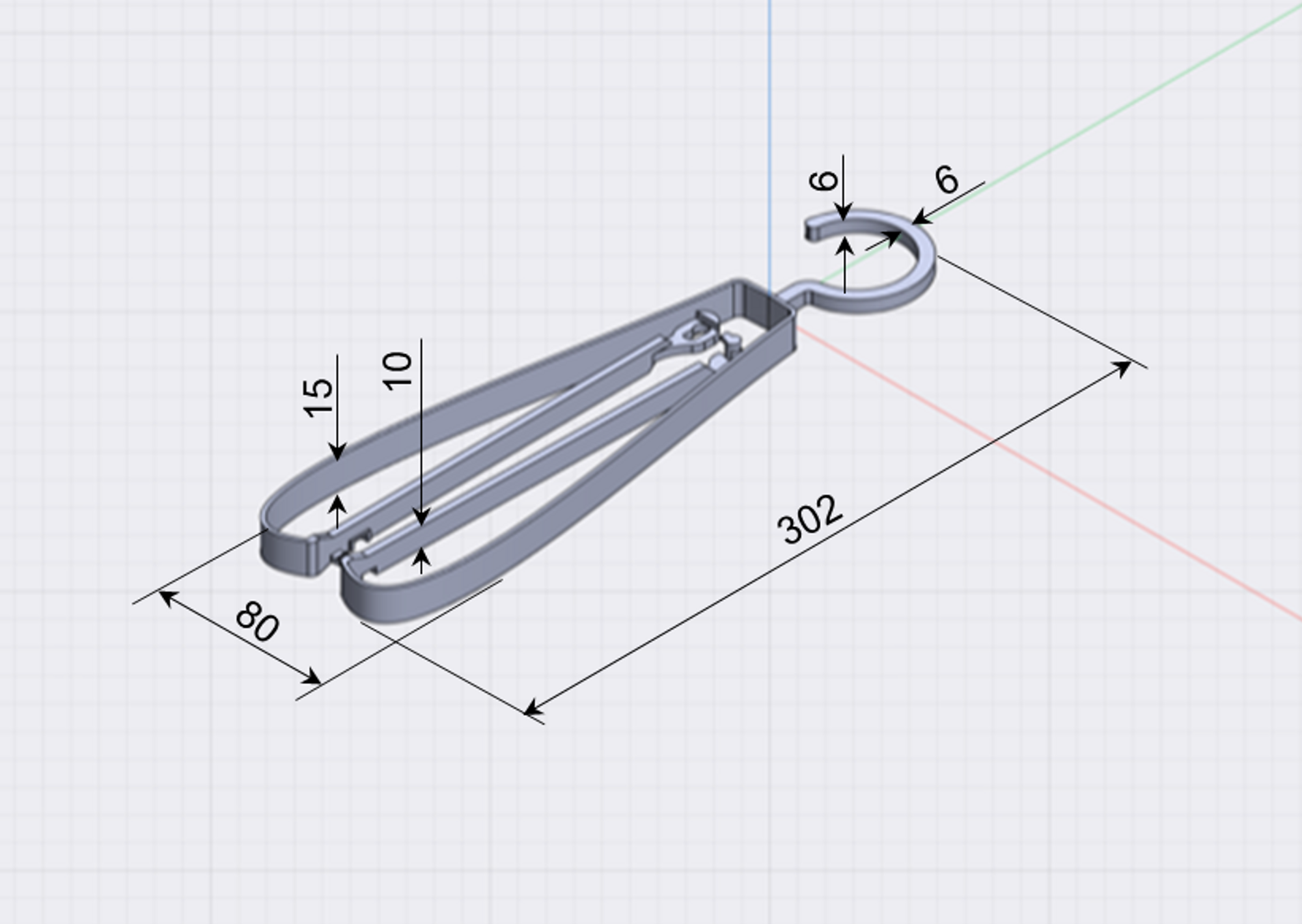
折りたたみハンガーの初期設計形状
-
溶融プラスチックは充填可能か?
-
肉厚は適当か?
- 成形加工時間が長すぎないか?
-
厚みは小さくできるか?
フック部で6mmと厚いために、射出成形プロセスにおける「冷却時間」が長くなることが予測できます。厚みを小さくする必要があります。
平板における非定常熱伝導から、冷却時間は次式で表されます。(参考文献:Rao,Natti S.: Design Formulas for Plastics Engineers, Hanser, Munich(1991) p.50 )
t_c = \frac{1}{\alpha} \Bigl(\frac{h}{\pi}\Bigr)^2 \space ln \Bigl[ \frac{4}{\pi} \space \frac{T_d - T_i}{T_d - T_e} \Bigr]
ここで、t_c : 冷却時間、\alpha : 熱拡散率、h : 肉厚、T_d : 金型温度、T_i : 射出される溶融プラスチック温度、T_e : 取出可能温度であり、熱拡散率は次式で表されます。
\alpha = \frac{k}{\rho \space c_p}
ここで、k : 熱伝導率、\rho : 密度、c_p : 比熱。
冒頭に書いた物性値、成形条件より冷却時間を求めます。最大肉厚 h = 6mmのフック部に対して、離型可能(金型から部品の取り出しが可能)な状態となる時間は、上式より、冷却時間は
t_c = 35s
と予測できます。
充填時間 t_f = 1s、保圧時間 t_h = 10s、 型開~型閉の時間 t_k = 10sとすると、成形サイクルタイムは、上記の合計であり、
t_{cycle} = 約56s
と予測できます。
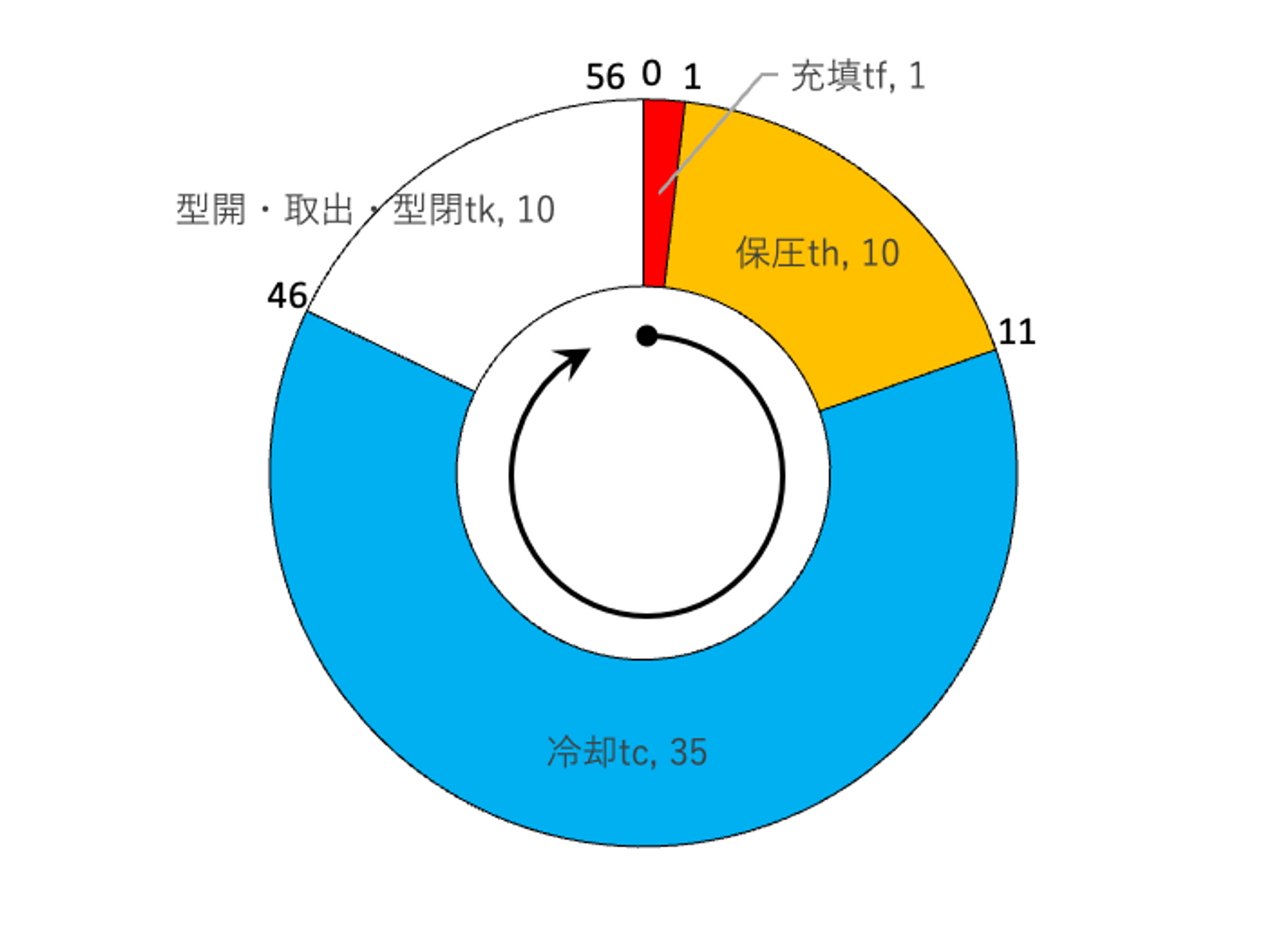
補足 : サイクルタイムの予測について。
厳密には、溶融した高温のプラスチックは充填開始時点から金型壁面に接して冷却が始まっています。充填過程においては、冷却よりも入熱が支配的なので、充填完了後の保圧過程から冷却が開始すると仮定するのは実用的です。また、保圧過程は冷却により収縮していく溶融プラスチックを補充することを目的にしており、すなわち熱流入が継続されます。保圧時間 t_h=10sとしていますが、これは成形機での機械制御の設定であって、熱流入はその途中で止まる可能性もあります。したがって、実際の冷却時間は保圧時間を含めると考えることもできます。
しかしながら、この計算式では入熱は考慮しておらず、厳密に冷却に要する時間を見積もることはできません。すなわち上記の理論式で推測できる成形サイクルタイムは 46〜56s の範囲にあり、予測にはばらつきがあると認識すべきです。仮に保圧時間の半分を採用すると、サイクルタイムは 約51s と見込むこともできますが、初期検討では保守的に見積もることにします。型開から型閉までのいわゆる「ドライサイクル t_k」についても設備機器の設定で高速化が可能ですが、ここでは同様に保守的に見積もっています。
次に、Moldflow による計算結果を示します。Moldflowによる計算では、入熱と冷却を連成して計算するので、より現実的な予測となっています。離型可能となる十分に冷却される時間は、次のように計算されました。
t_f + t_h + t_c = 42s
これより、成形サイクルタイムは約52sと予測できます。
離型可能時間における温度分布(z方向中央の断面)を示します。これより厚みの大きいフック部の温度が高い、すなわち冷却に多くの時間を要することがわかります。逆に、この部分の厚みを小さくすることで、サイクル時間を短縮することができます。
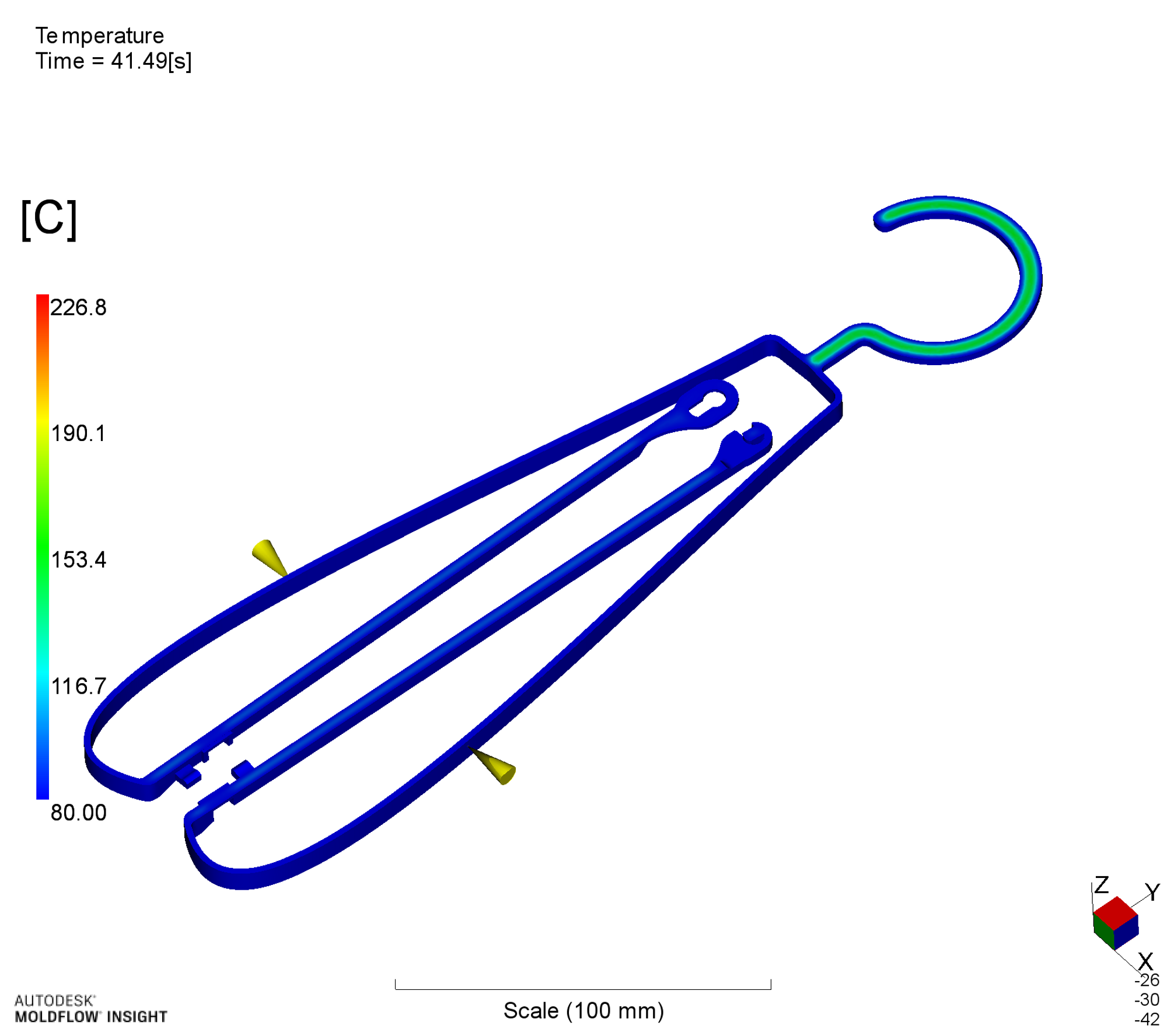
離型可能時間における温度分布(断面)
補足:上述した理論式とMoldflowでの(今回の)計算ではどちらも、厚み方向の温度がすべてT_eに到達した場合(100%固化した場合)に離型可能としています。しかしながら実際には、例えば内部が高温で溶融状態にあっても表層の固化が進んで離型可能な場合もあります。100%固化していなくても成形不良なしに離型可能な金型設計を進めることも重要です。具体的には、エジェクタピンを適正に配置すれば、取出し時に無理な力がかからず、変形させずに取り出すこともできます。
ただし、離型時間を変えることによって部品内で冷却状態に差が生じることに注意が必要です。特に結晶性プラスチックでは結晶化度が変わり、その結果収縮率が変化します。収縮率の変化は成形品の寸法、そり変形に影響し、商品設計時点で予測していなかった成形不良発生の可能性があります。手戻りをなくすためにも、商品の機能設計と生産設計の同時進行は重要と考えます。
この商品に求める機能(第1部参照)から、直線部とフック部には一定の剛性が必要です。したがって、サイクルタイム短縮のために単純に厚みを小さくするのではなく、例えばH字状の断面形状とするような形状(肉盗み)の採用が必要です。これにより、冷却時間を短くするとともに、一定の剛性を確保することができます。
-
金型から成形品は抜けるか?
- アンダーカットとなる形状がないか?
-
抜き勾配はあるか?
この部品(ハンガー)を床面に置いた状態の平面をxy面とします。部品は金型をz方向に開いて取り出す(離型する)ように配置します。この部品はパーティング面(PL:パーティングライン)をxy平面、z方向の中央(z=0)とします。z方向が抜き方向であり、部品を離型させるためには第一に「アンダーカット」形状がないことが求められます。アンダーカットがあっても、金型にスライドコアを設けることで離型可能とすることはできますが、金型が高価になることから、できるだけアンダーカットのない形状設計をしたいところです。この部品の初期検討段階から、すでにアンダーカットのない設計となっています。
さらに、離型時の成形不良を起こさせないために、適正な「抜き勾配」を設けることは必須です。一般に抜き勾配は0.5または1度以上とします。初期構想では抜き勾配を設けていないので、設計変更が必要です。
補足:射出成形においては、金型の可動側(型開時に金型でエジェクタピンの配置される)に成形品が残っている必要があります。この商品はz方向中央から+z、-z方向に鏡面対称ですので、同じ離型抵抗であるならば、具体的には同じ抜き勾配としたなら、成形品を可動側に確実に残すことができません。この不安定さを避けるためには、例えば固定側の抜き勾配を可動側よりも大きくすることでこれを実現します。
しかし、そうするとz方向の対称性が崩れてしまいます。この商品の機能として、対称性が崩れる影響度合いを確認しておく必要があります。本報では、対称性が崩れることによる商品機能への影響を検討していません。
射出成形について考慮した設計案
前節で説明した要件に配慮した設計案を示します。フック部断面はH字状に、直線部はT字状にすることにより、薄肉化とともに必要な剛性を確保する形状としています。
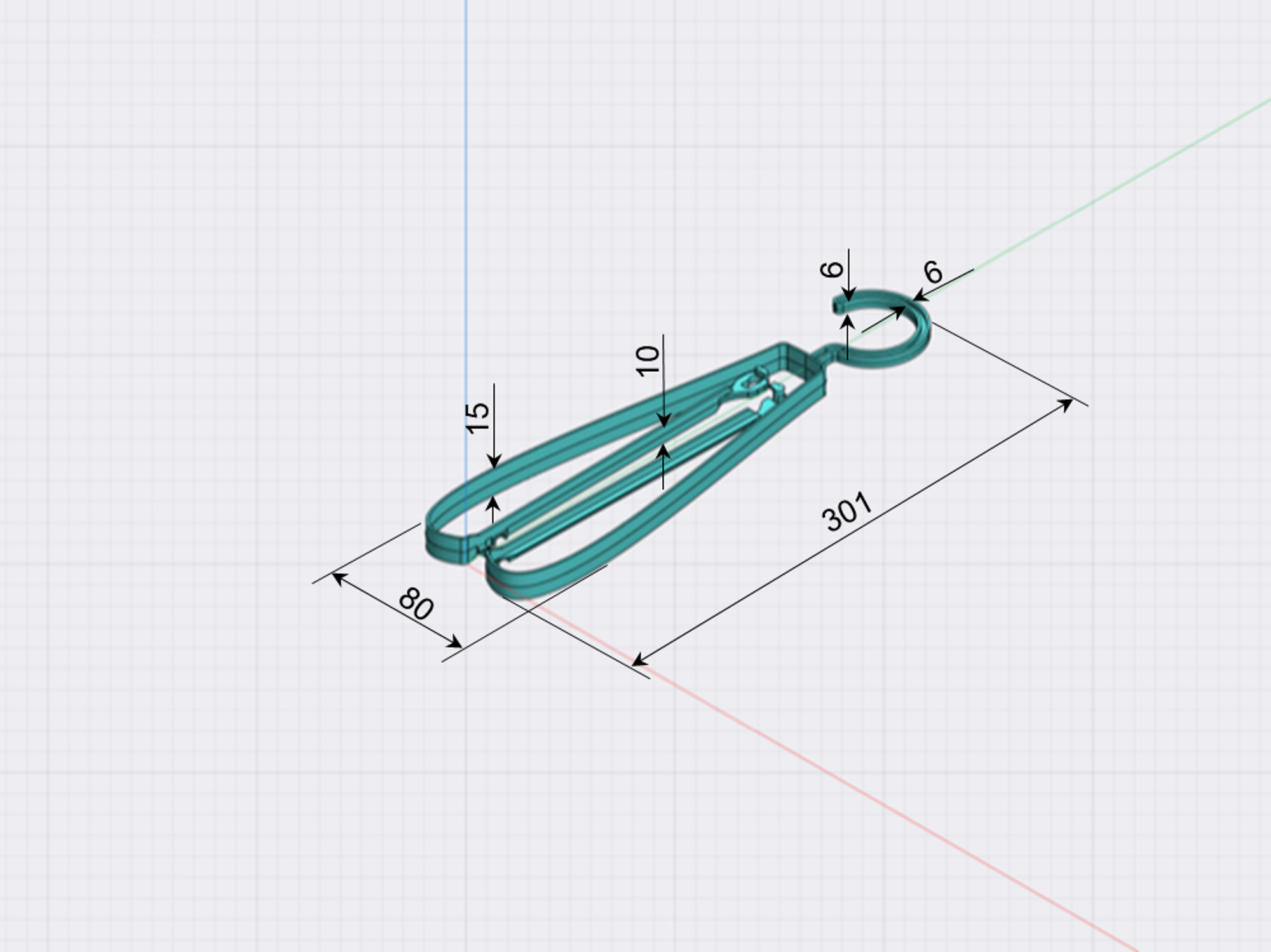
成形加工を考慮した形状案
同設計案について一部の断面寸法を示します。z方向中央より上下に抜き勾配を設定。T字部リブ(図中、横に突き出している部分)の厚みは、後述する成形でのそり変形を極小化するための変数とし、初期値を1mmとしています。なお、リブ厚みを1~2mmで変化させても設計意図を満たすことが事前の検討により確認できています。
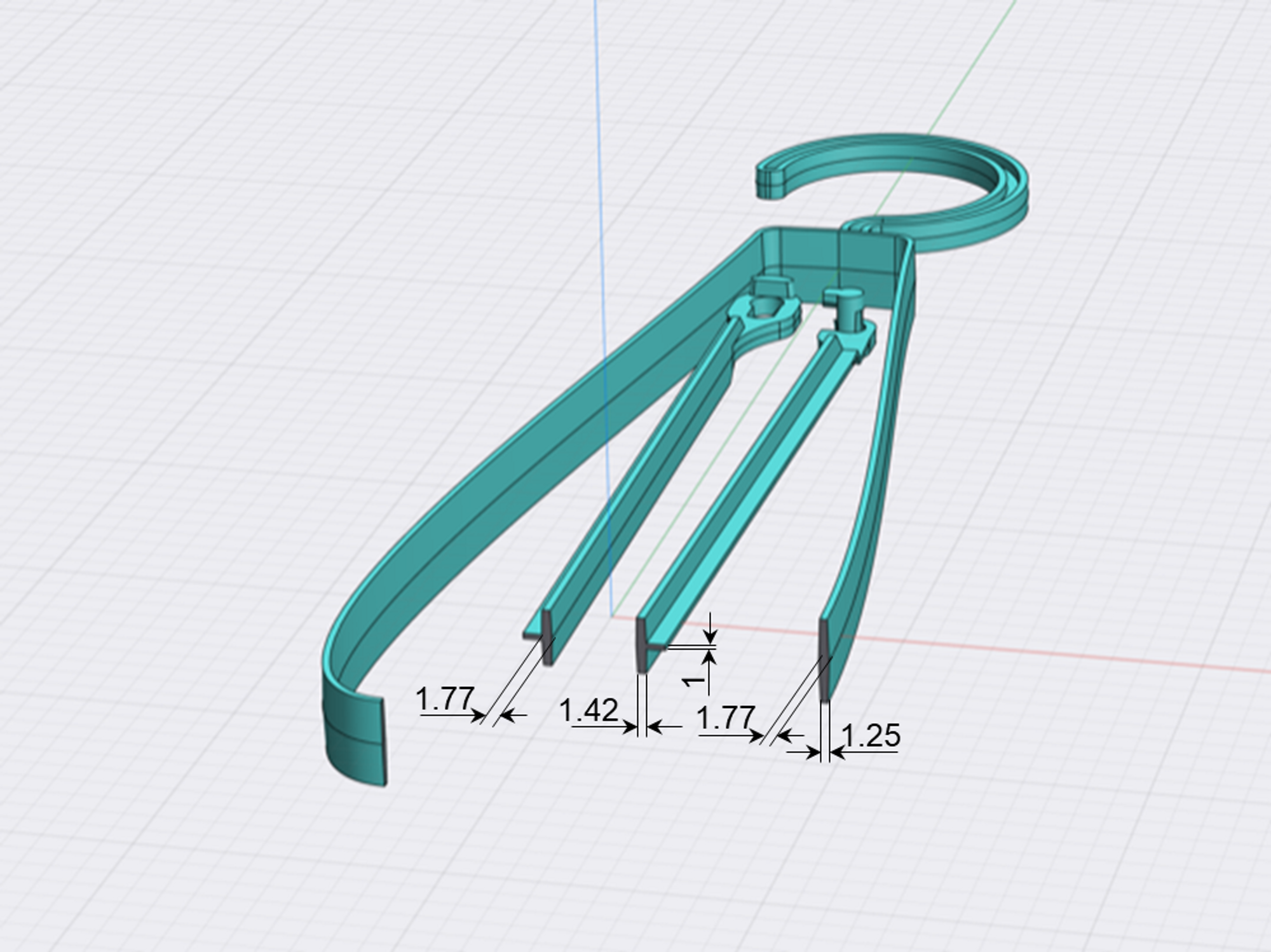
成形加工を考慮した断面形状案
成形加工性の評価
ここまでで、射出成形での量産実現性を考慮した形状を決定できました。次に、Moldflowを用いて成形不良の発生がないかの確認を進めます。
簡略化:ここでは、ランナーは配置せず、ゲートからの溶融プラスチックの充填だけで評価します。すなわち、仮に複数のゲートを設けるとしたら、それらより同時かつ均等に分配された溶融プラスチックが充填されるものと仮定することになります。これは、次のステップである金型設計にて、ランナーバランスを適正に設計することを期待するものです。同様に金型冷却管も、この段階では配置しません。すなわち、溶融プラスチックが接する金型壁面から均一に冷却されることを仮定することになります。実際には、ハンガー内側を構成する部分については、相対的に冷却しにくいことが予想されます。金型設計においてできるだけ均一冷却となる冷却管レイアウトが実現できることを期待した検討となります。実際には、冷却管を配置できないところもあり、不均一な冷却によりそり変形が大きくなることは予測できます。すなわち、形状修正など設計の手戻りが発生することを認識して、検討を進めることになります。
以下、成形不良現象を想定しながら、計算結果を確認していきます。
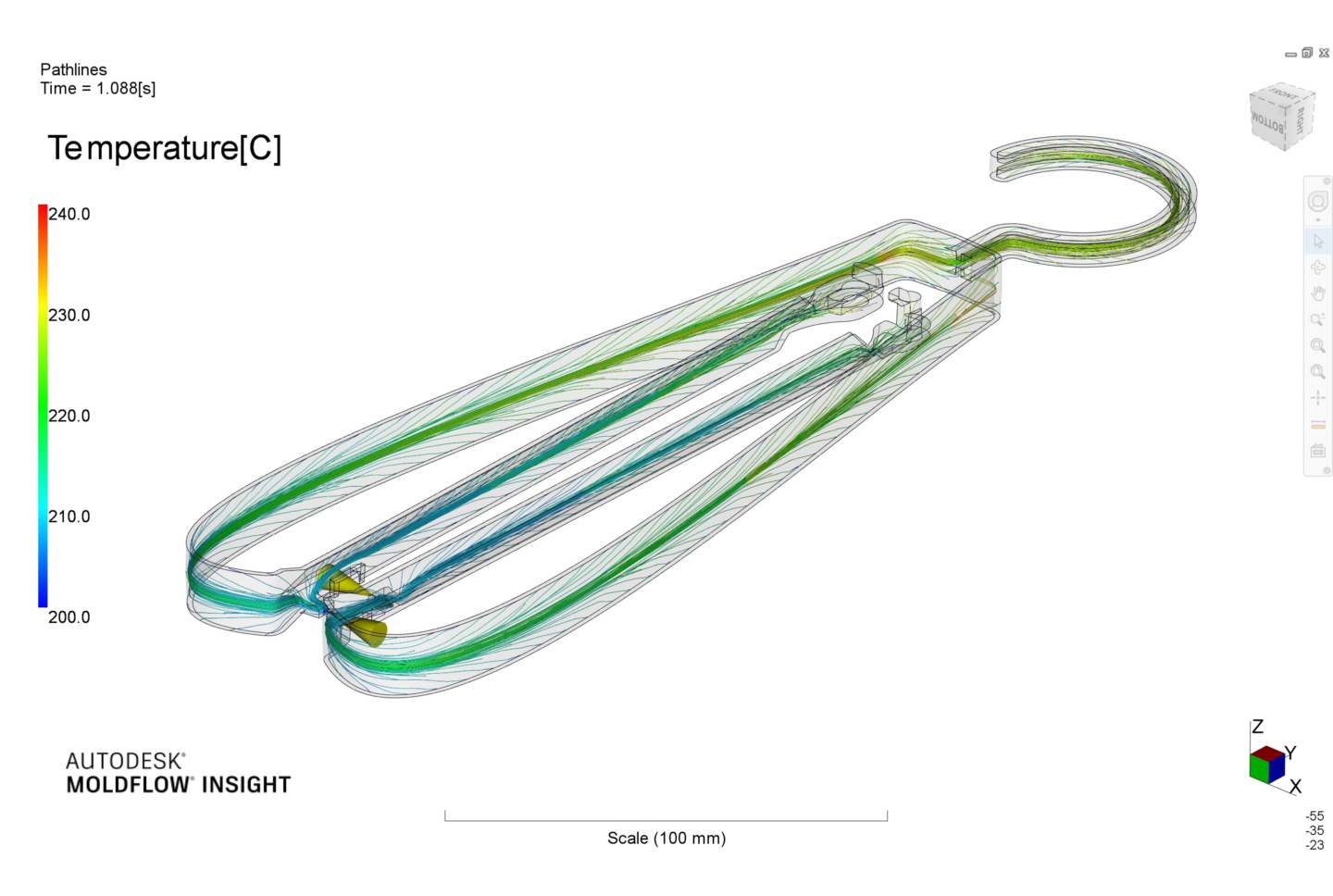
計算に用いたメッシュ(表面のみ表示)を示します。図の左下部のコーンで示した2つの位置をゲートとしています。実は、弓部に2箇所のゲートを配置することにより、3箇所の最終充填位置(流動末端)への同時充填が実現できます。しかしながら、この弓部が薄肉であること、直線部に対する充填・保圧を十分とする(これにより、直線部の収縮を小さくする)ことを意図して、この2つのゲートとしました。

メッシュ分割(3D)
1) 未充填不良(ショートショット)は起こらないか?
充填末端となる3か所への同時充填は実現できていませんが、射出率を50cm^3/sと比較的高くとったこともあって、未充填不良の発生はありません。
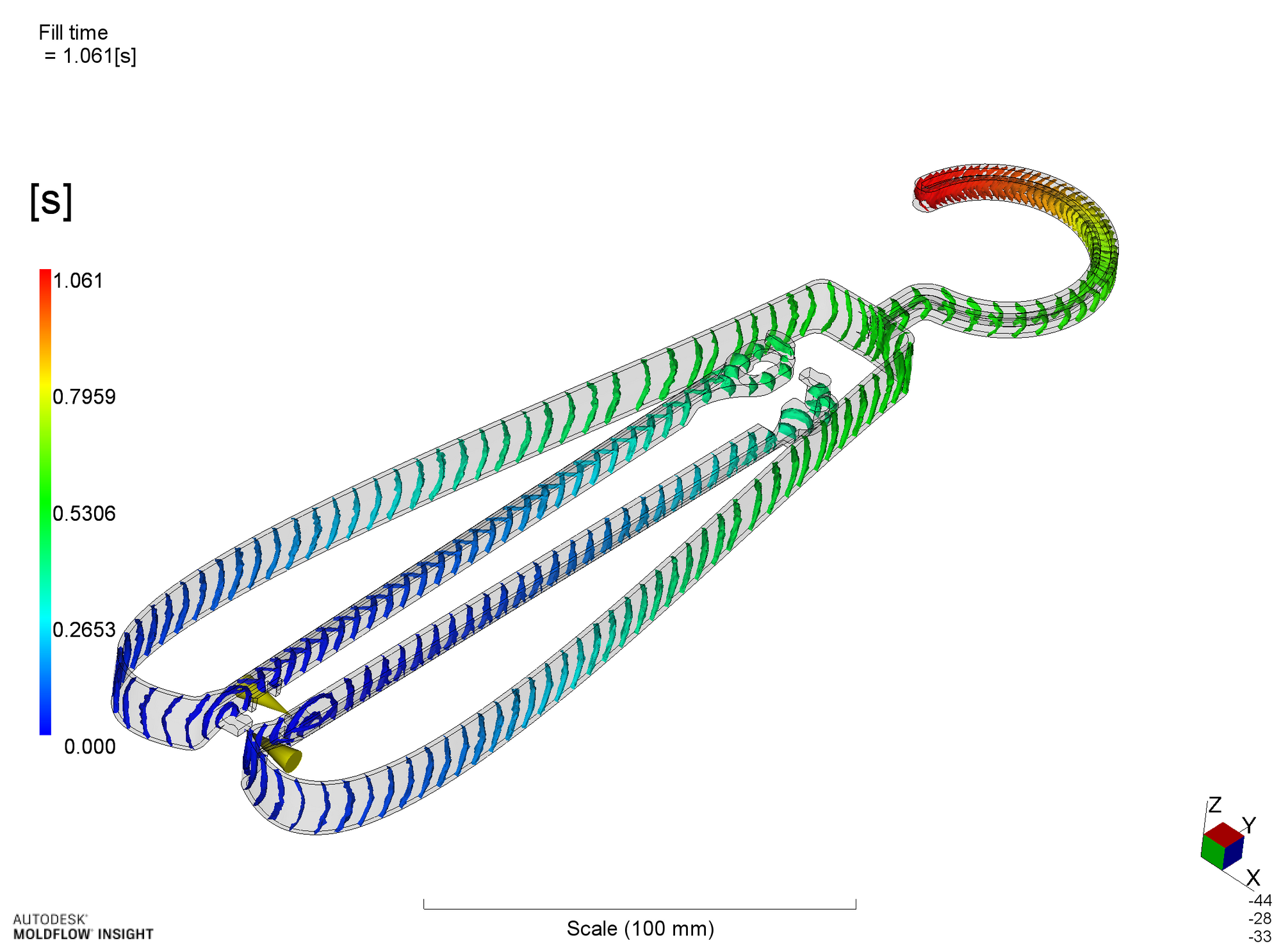
溶融プラスチックの金型内流れ
フローフロント(充填中の流れの先端)の溶融プラスチックの温度分布を次に示します。充填途中での温度低下が大きい場合は、固化して未充填不良となますが、本件では温度低下は認められません。逆に、高粘性流体であるがゆえに、せん断発熱が起こり、流入温度である200℃より高温となっています。
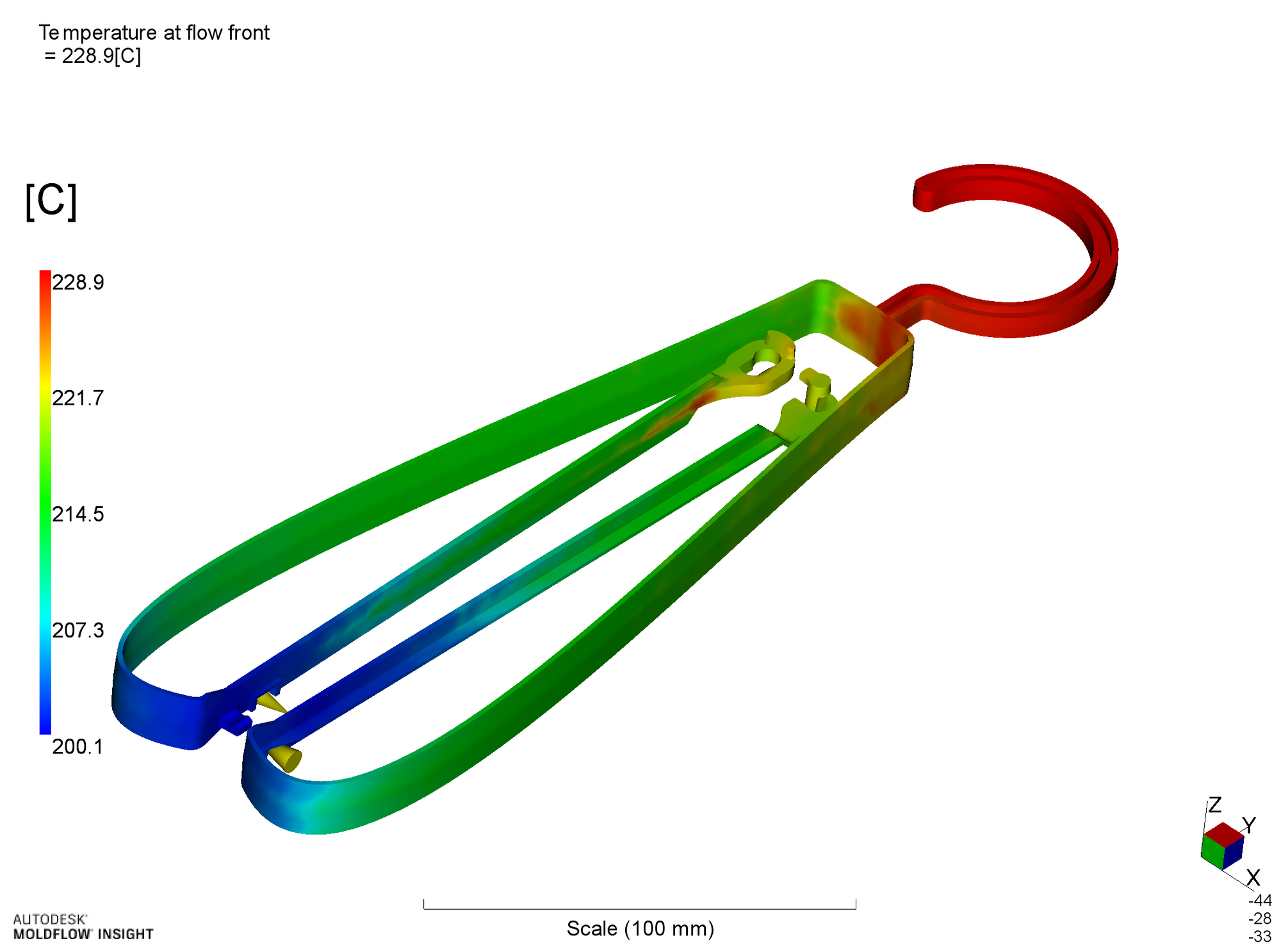
フローフロントでのプラスチック温度
2) 強度が低下するウェルドラインの発生はないか?
ウェルドライン発生位置を示します。
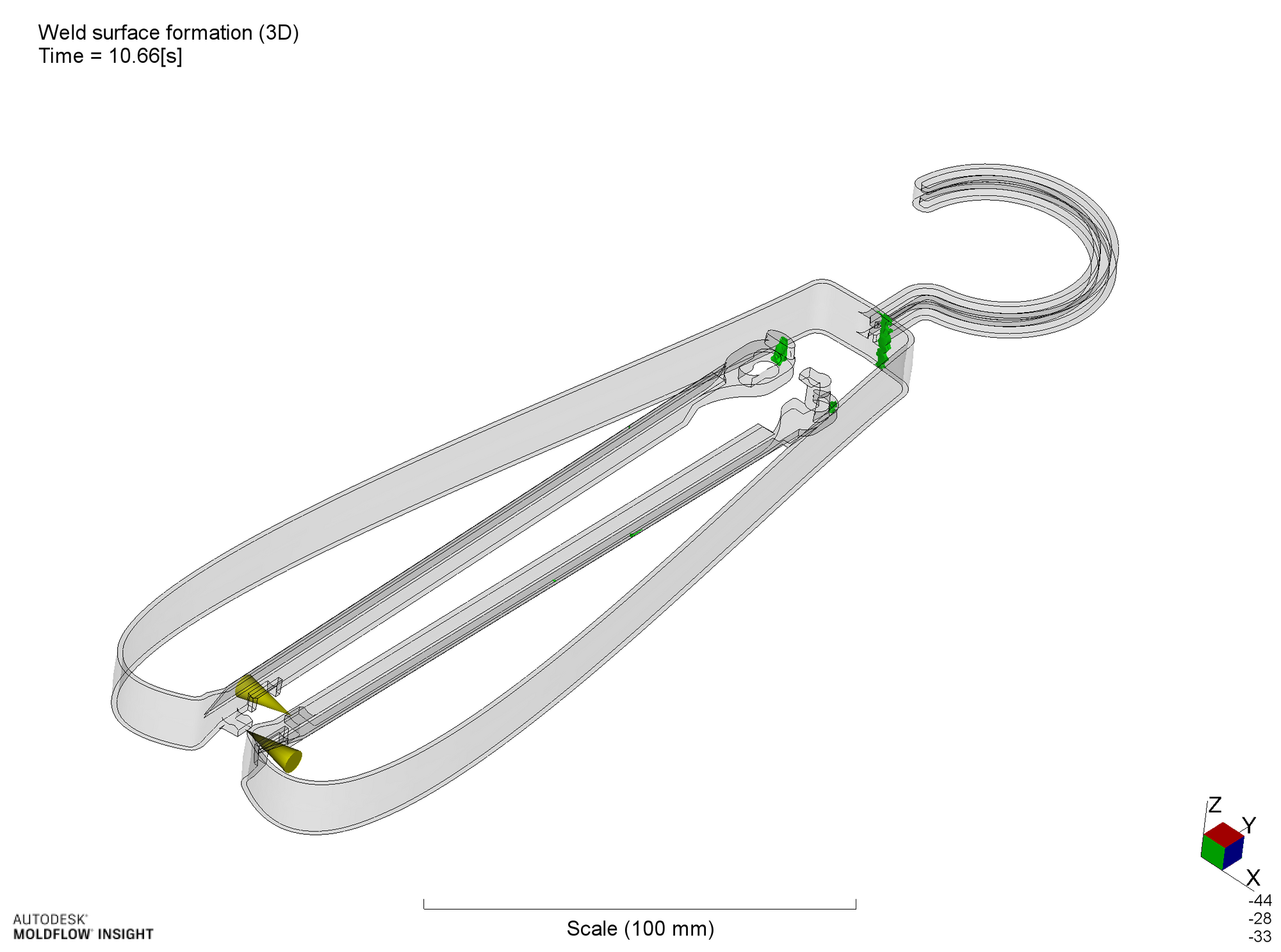
ウェルドライン発生位置
直線部の両端にウェルドラインの発生が予測されます。特に孔側(図の左側)については、孔を形成する部分を迂回する流れの会合が起こります。ここについては、充填末端であることから、速度変化によるウェルドラインの強度低下抑制(後述)を期待できません。
商品機能として、この穴部を末端側に引っ張るような力は作用しないので、強度低下があっても問題はないことが期待されます。期待しますが、一般にウェルドライン部の強度低下を定量的には予測できませんので、実際に作成して試験を行い、強度低下が無視できないならば改善が必要となります。本報告では、ここまで言及しません。
フック付け根付近には、左右の弓部からの流れが会合しています。ここがウェルドライン発生位置と予測できますが、ここは流動末端ではなく、会合後にフック部への流動が継続します。衝突部では図の右から左への逆流も起こって、さらに流動が継続し、高分子の絡み合いが特に内層部で起こります。これにより、この部分の強度は大きく低下しないと考えられます。
確認のために、流速の変化を下に示します。
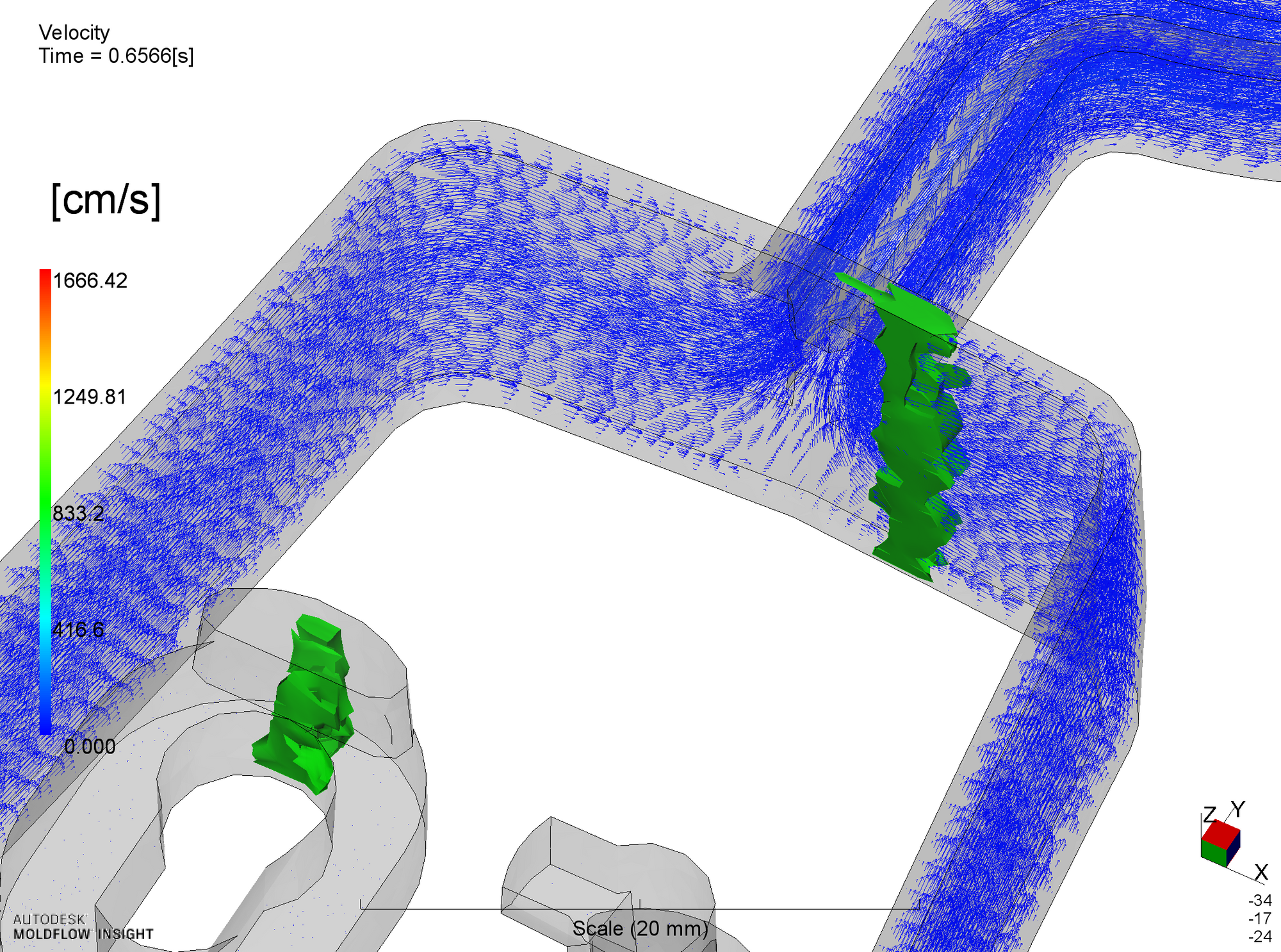
溶融プラスチック会合後の流速
3) 冷却時間は適正か?
z方向中央断面におけるプラスチックの温度分布を示します。図は離型可能となった時間、充填開始から約11s後の温度分布です。初期形状(離型可能までの時間:約42s)から、全体として厚みを小さくした結果、成形サイクル時間は約11sと大幅に短くできます。
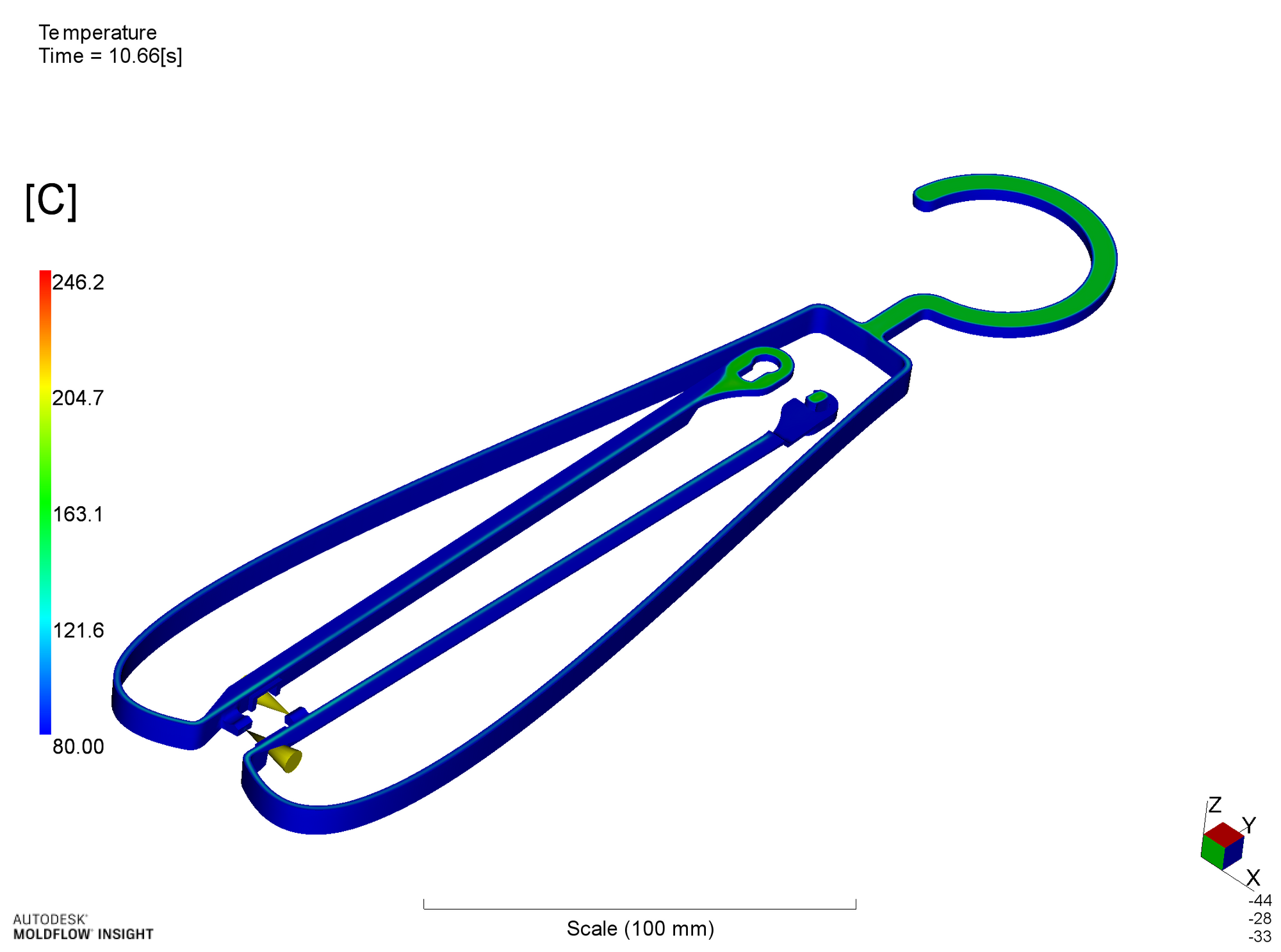
離型可能時間におけるプラスチック温度(断面)
4) ヒケの発生はないか?
ヒケの発生量を下図に示します。ヒケ(くぼみ)は最大で0.04mm程度と大きくはありませんが、特に光沢のある表面ではヒケが目立つ可能性はあります。また、後に検討する直線部の反り変形対策としてのT字部リブの厚みが大きくなる場合、直線部にもヒケ発生の可能性があります。この計算結果では直線部にはヒケ発生が予測されていません。
基本的には、本商品の機能上ヒケは大きな問題(外観不良)になることはありません。もし必要であれば(ヒケが気になるようであれば)、表面にシボ加工をすることで光沢をなくし、ヒケを目立たなくすることもできます。

ヒケ(変形量)
5) 反り変形は過大ではないか?
以下にx、y および z方向の反り変形量を示します。
x方向の変形では、弓部での変形が直線部との境界近傍で大きな変形として表れていることがわかります。弓部については、この程度(1.5mm)の変形は問題ではありませんが、直線部の変形(曲がり)については、ハンガー組立時に直線部に圧縮力が作用することから、過度な曲がりは無視できません。
次ステップにて、この直線部の変形について、リブ厚みとの関係を確認し、適正なリブ厚みを決めることにします。
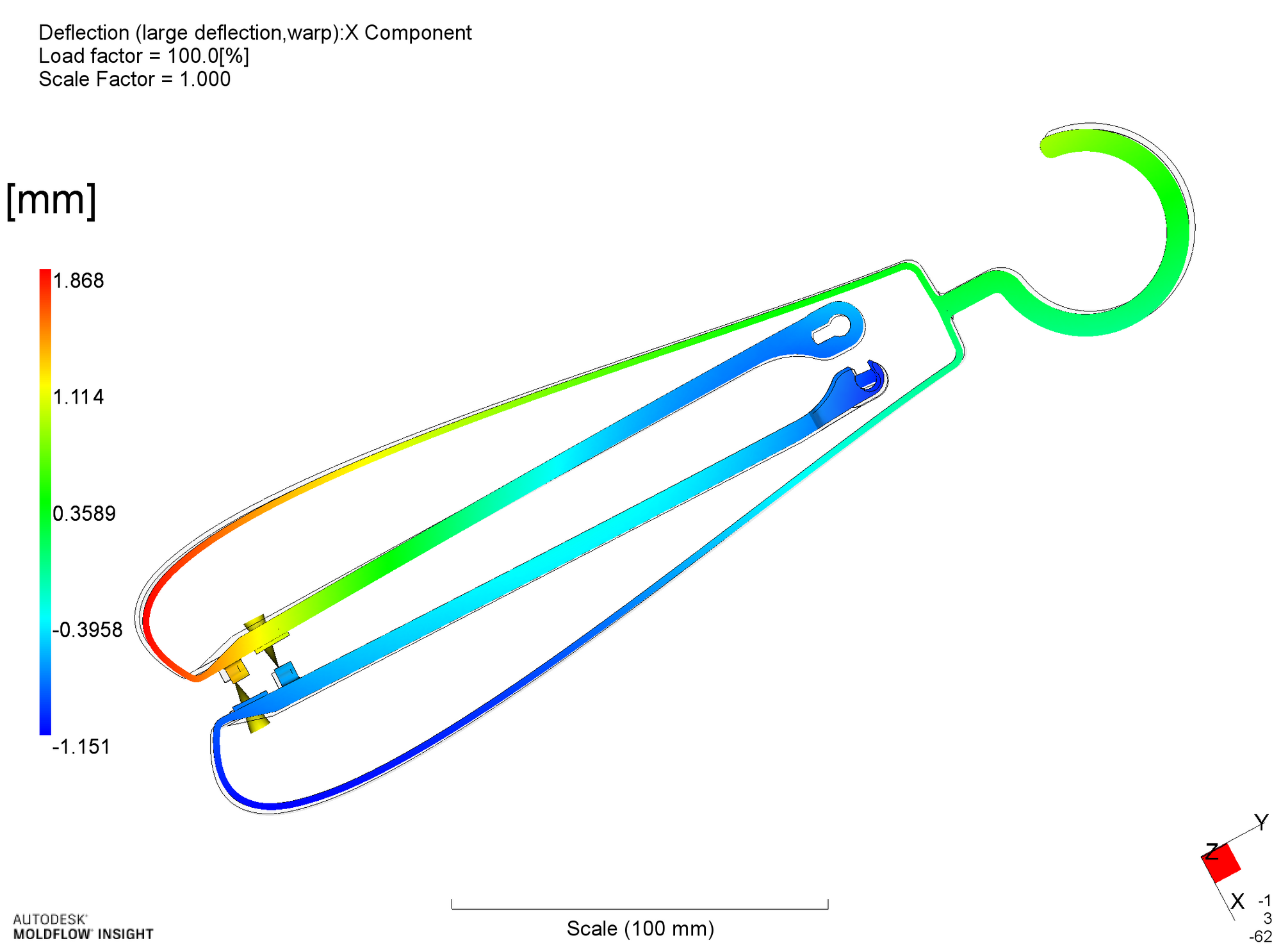
反り(x方向変形量)
y方向の変形量からは成形収縮による寸法の変化を見ることができます。特に直線部については寸法の設計からの違いについて、機能としての確認をしておく必要があります。

反り(y方向変形量)
z方向の反りはxy平面外の変形を示しています。計算結果は0.2mm程度であり、問題とはなりません。実際に配置可能な冷却管によっては、不均一な冷却のために反りが大きくなる可能性は残っています。適正な冷却管により反りを低減させることができます。本報では、冷却システムの設計については言及しません。
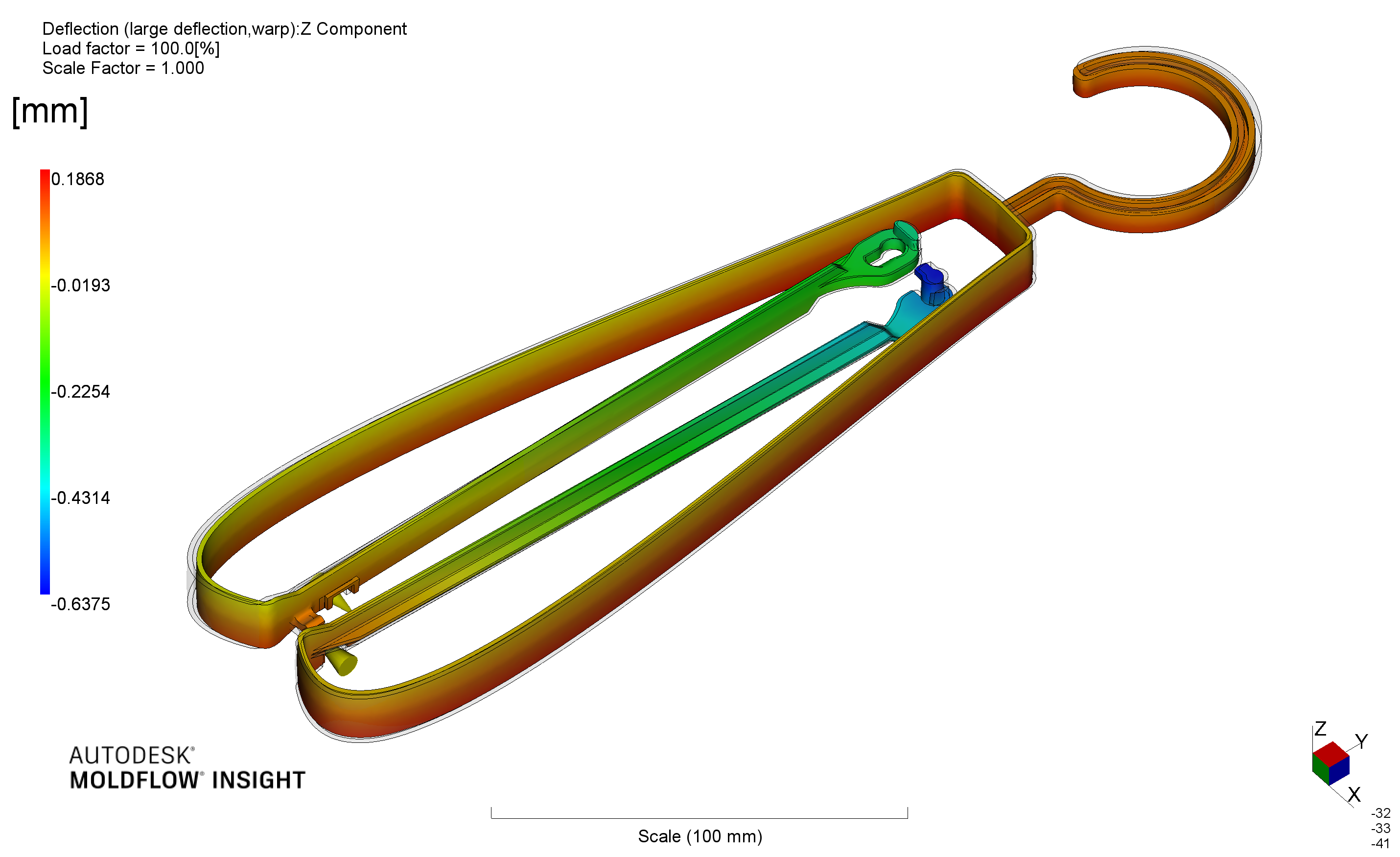
反り(z方向変形量)
反り変形を最小にする
直線部におけるリブの厚み(初期値は1mm)を、1.2, 1.4, 1.6, 1.8, 2.0mmと変化させて、直線部の曲がり量を確認します。ここでは、弓部を含む全体としての変形ではなく、直線部の曲がりのみを確認します。そのために図に例示するように、直線部の一端をピン固定(x,y,z方向の変形を固定、回転は自由)、他端についてはx方向と回転を自由として中央部のx方向変位を求めます。ここで図の下方向がx方向の正なので、下方向に凸に曲がった場合、変形量は正の値となります。この測定方法は、2つの直線部ともに同じなので、同じ形状であれば両者の変形量はプラスマイナスが逆に表されることになります。
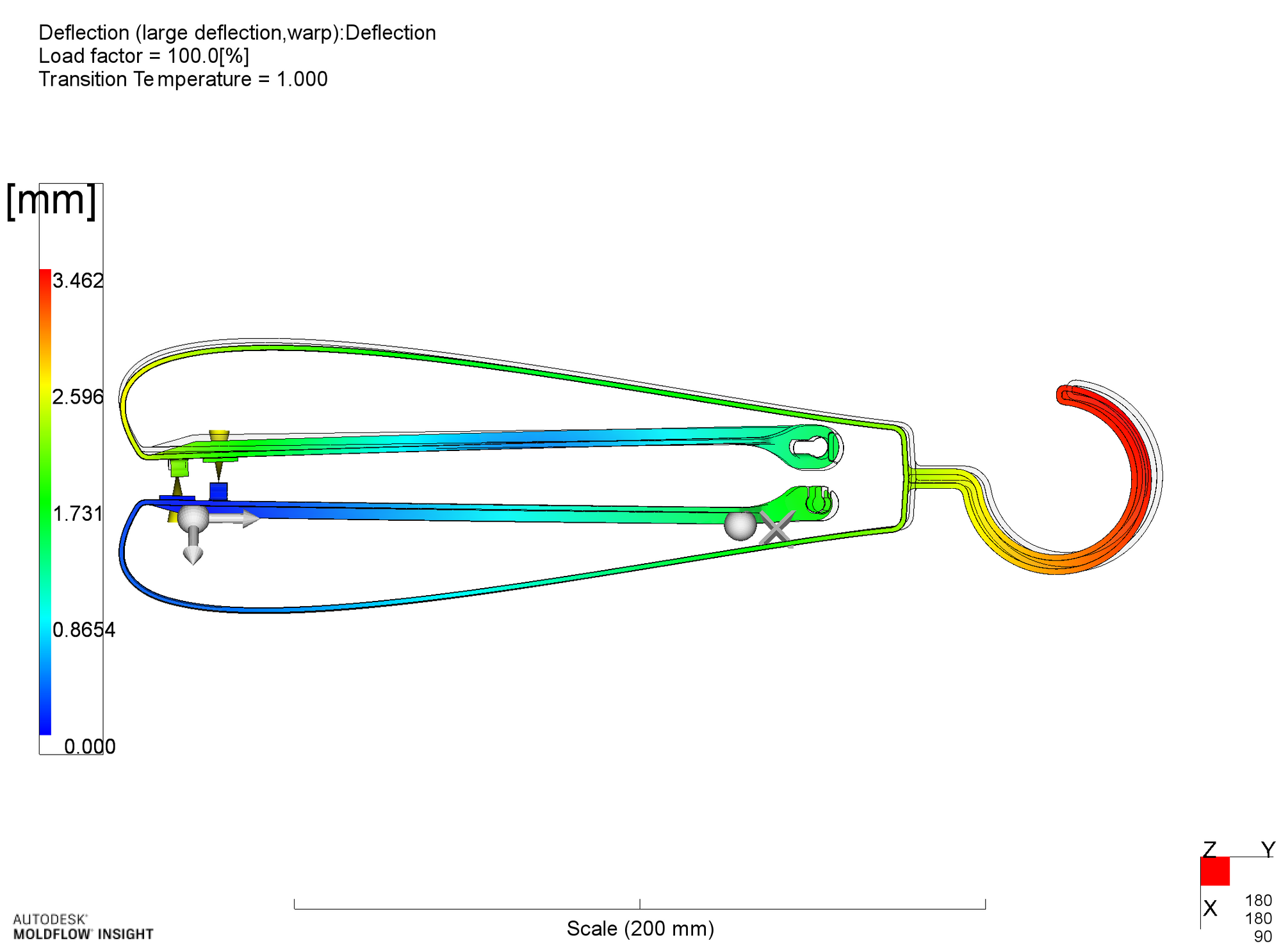
直線部での局所変形を見るための固定
リブの厚みと直線部の変形の関係を確認します。そのために、リブ厚みを h_r = 1.0, 1.6, 2.0 と変えて、Moldflowによる計算を行いました。結果を以下に示します。
大きな変形では直線部先端が弓部に突き刺さって見えますが、本計算では接触を考慮していないためです。実際には弓部内側表面に接触するので、それ以上は変形は大きくなりませんが、拘束を受け応力として残存し、商品機能への影響は少なからずあります。
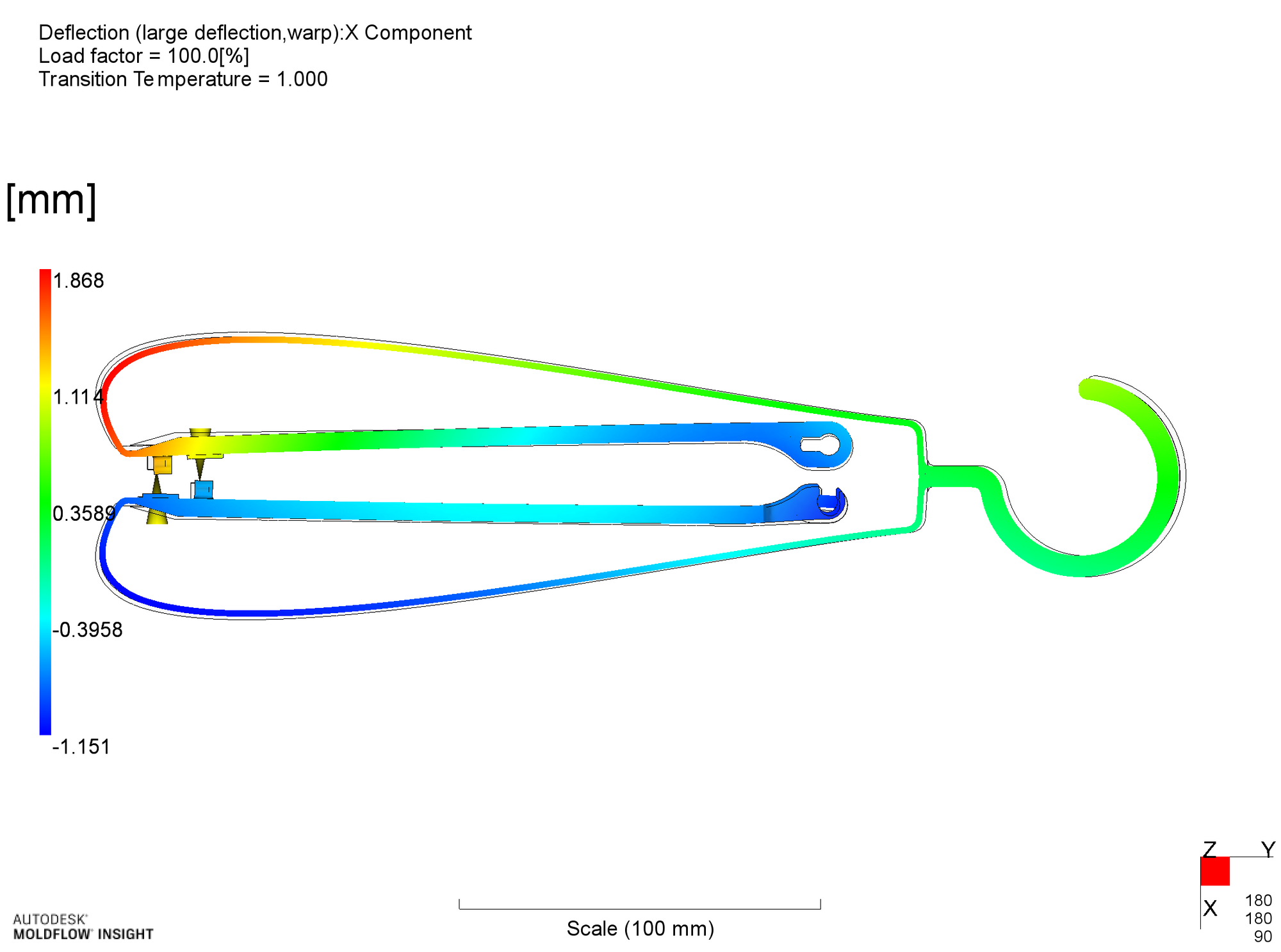
反り変形計算結果(x方向、h_r = 1.0mm)
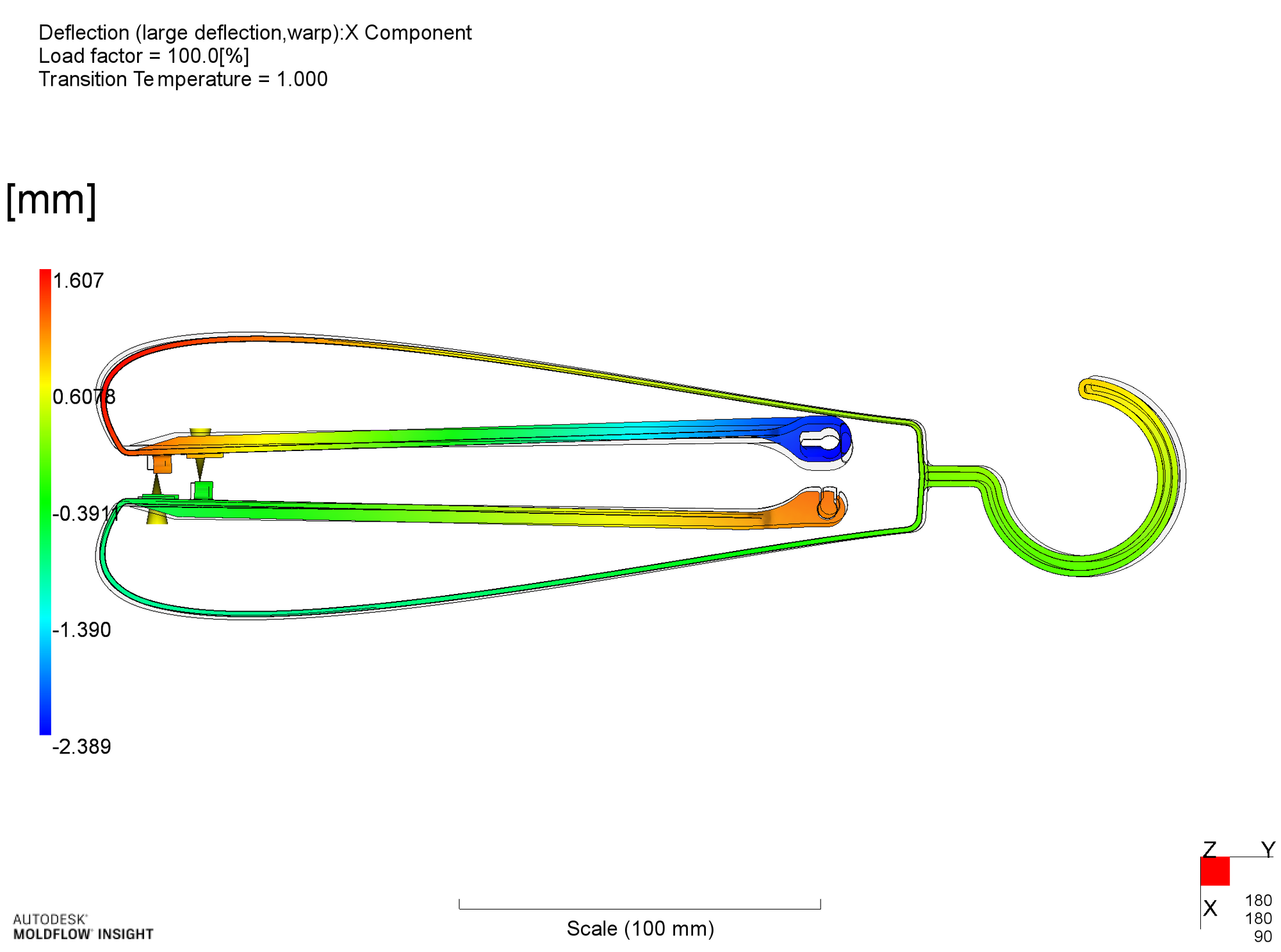
反り変形計算結果(x方向、h_r = 1.6mm)
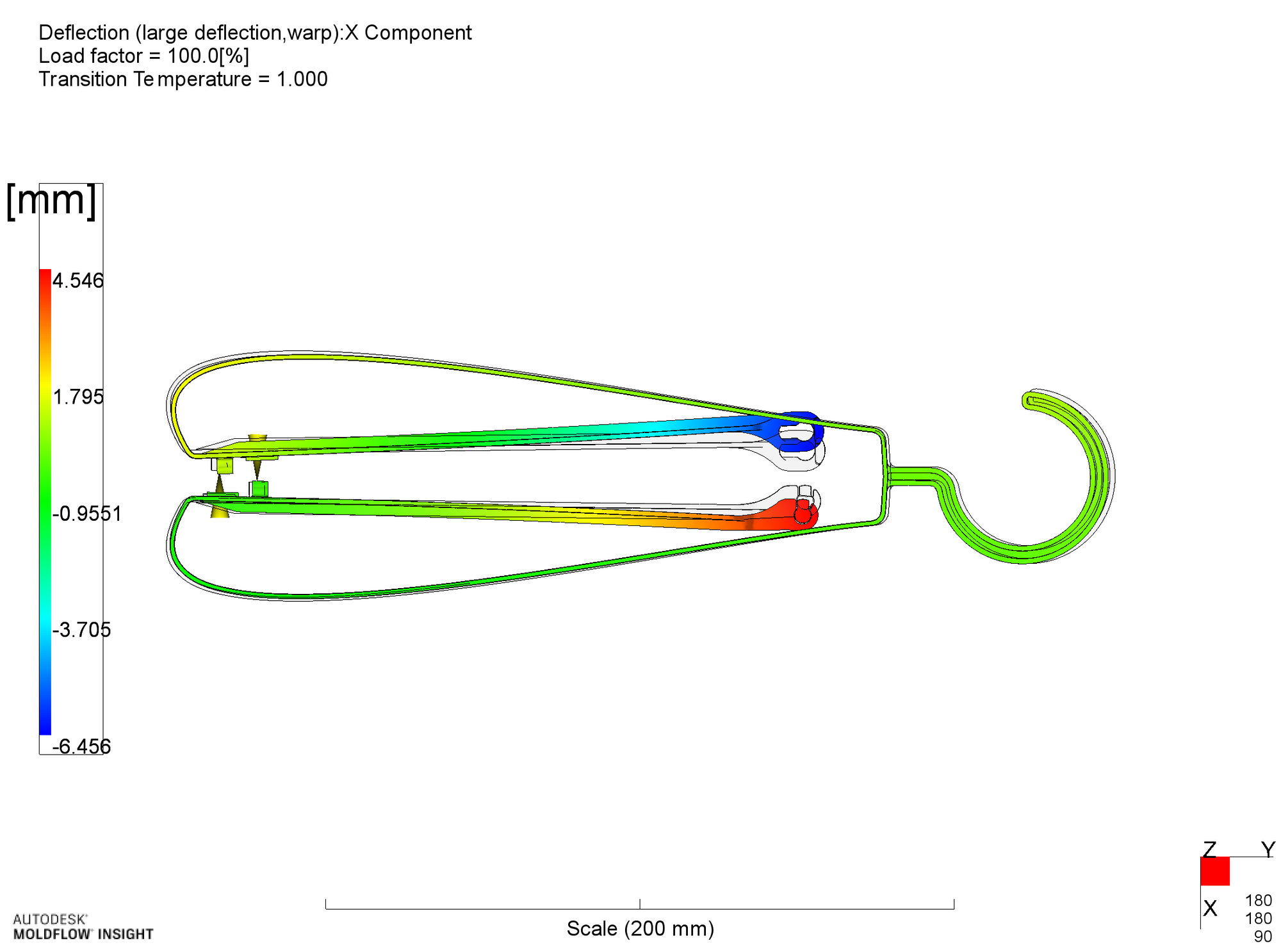
反り変形計算結果(x方向、h_r = 2.0mm)
以上の結果から、リブ厚みh_rとの直線部の変形(曲がり)の関係を次のグラフに示します。
これより、h_r=1.6mmで、変形は最小となります。
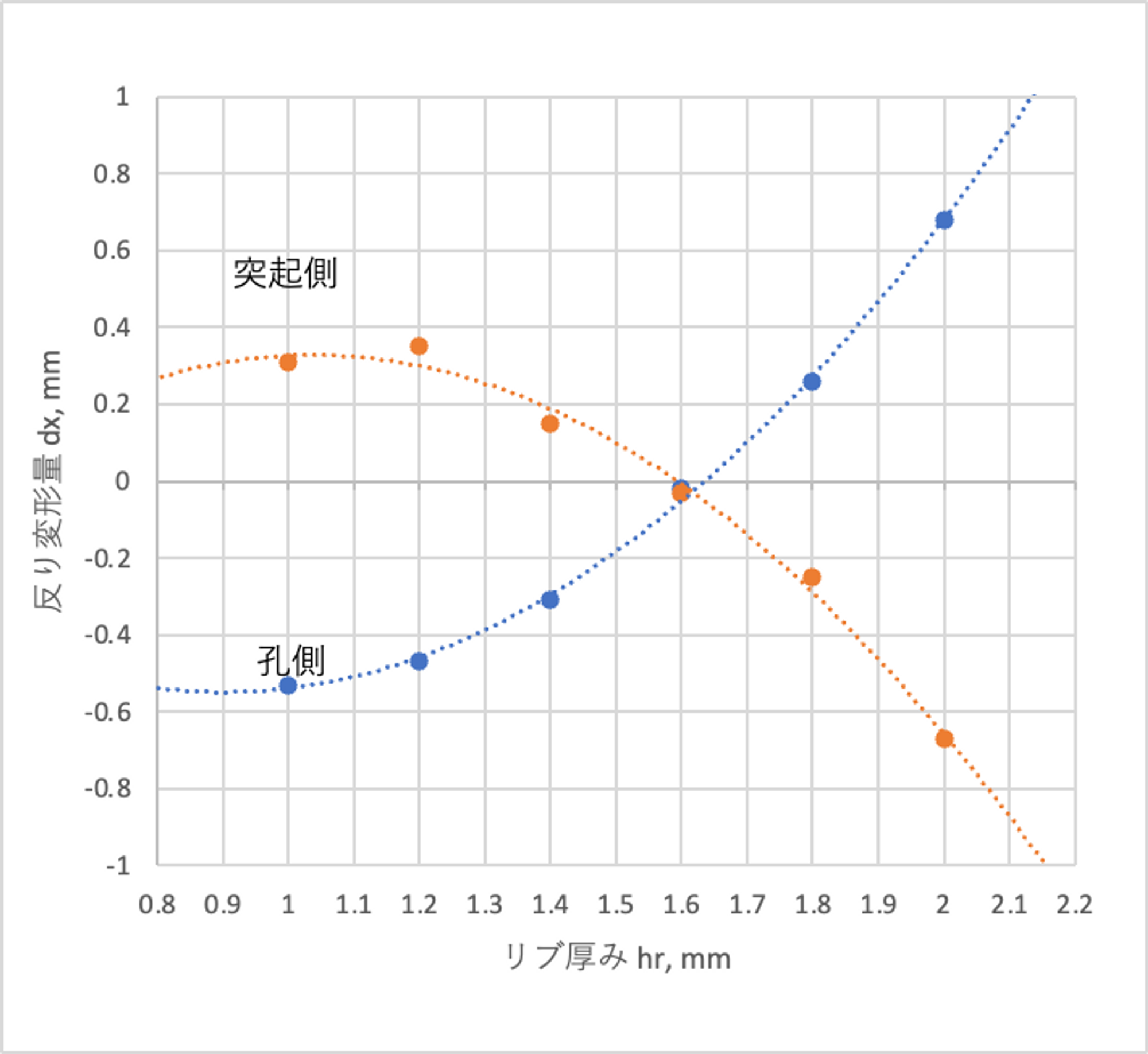
リブ厚みを変えた場合の直線部の変形
再確認
前節のように、直線部の変形を最小にするには、T字部のリブ厚みを1.6mmにすればよいことがわかりました。この寸法でのヒケを確認しておきます。
h_r = 1.0mmの場合に比べて1.6mmでは、ヒケは大きくなっていることがわかります。しかしながら、ヒケの量は0.001mm程度であり、問題にはなりません。
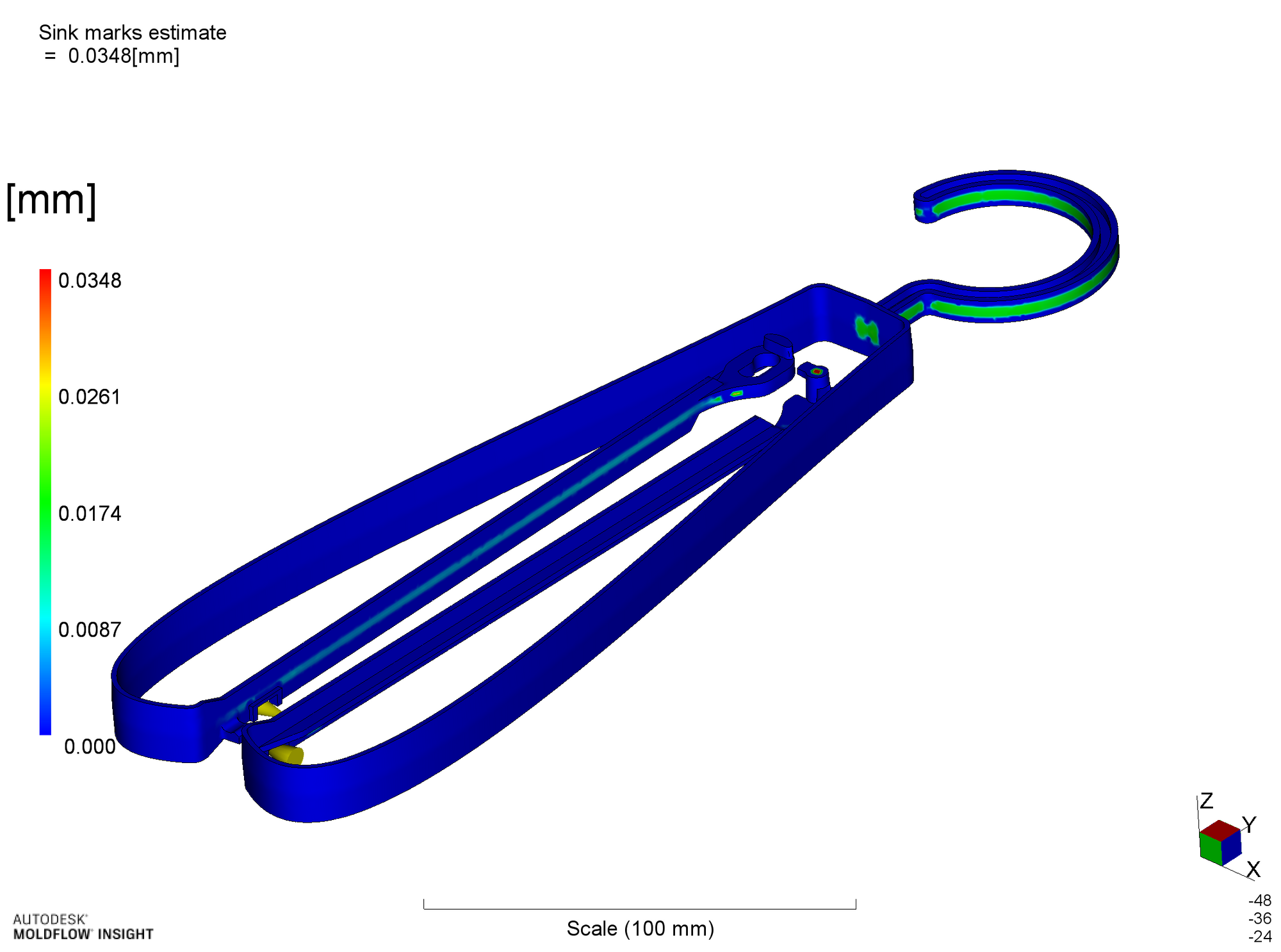
T字部のリブ厚み h_r = 1.6mmの場合のヒケの大きさ
まとめ
第1部で解説した新しい構造、機能を有する「折りたたみハンガー」ついて、既存の量産工法であるプラスチック射出成形で実現することを目指して検討しました。それに必要な検討項目について理論式やシミュレーションツールを用いて確認を行いました。
本報で金型設計要件については未検討で。溶融プラスチックの流動と冷却に伴い発生する成形不良現象を予測し、それを小さくするための形状設計として展開しました。これにより、量産可能な商品形状を決定することができました。
ここでは折りたたみ可能ハンガーの複数部品の一体化、またはコンパクト化によるコスト低減効果を示していません。これは次報にて解説する予定です。