VIDEO
はじめに
弾性変形を活用して力や動きを伝える機構をコンプライアントメカニズム(Compliant Mechanism)と呼びます。バネやプラスチック製品のスナップフィットなどもその一つです。
Nature Architectsでは、コンプライアントメカニズムを用いて複数部品で構成されていた製品を一体化することで、機能性向上や製造コスト低減を実現する設計を行っています。
この記事では「折りたたみハンガー」の設計を題材に、設計の考え方、社内ツールなどについて具体的な設計フローに沿って紹介します。
課題設定
携帯性や収納性を高めるために、折りたたむことができる衣類ハンガーは多数市販されています。通販サイトに掲載されている10製品について確認したところ、写真を見る限り3~10数点の部品の組み立てを必要とする設計となっていました。
本記事ではコンプライアントメカニズムを活用することで以下のような折りたたみハンガーの設計を行います。
設計コンセプト
一体成型可能な折りたたみハンガー
成形時にコンパクト(金型面積を効率的に利用できる)
設計する折りたたみハンガーの要件は以下とします。これらの要件は市販されている製品の平均的な寸法などから決定しました。
設計要件
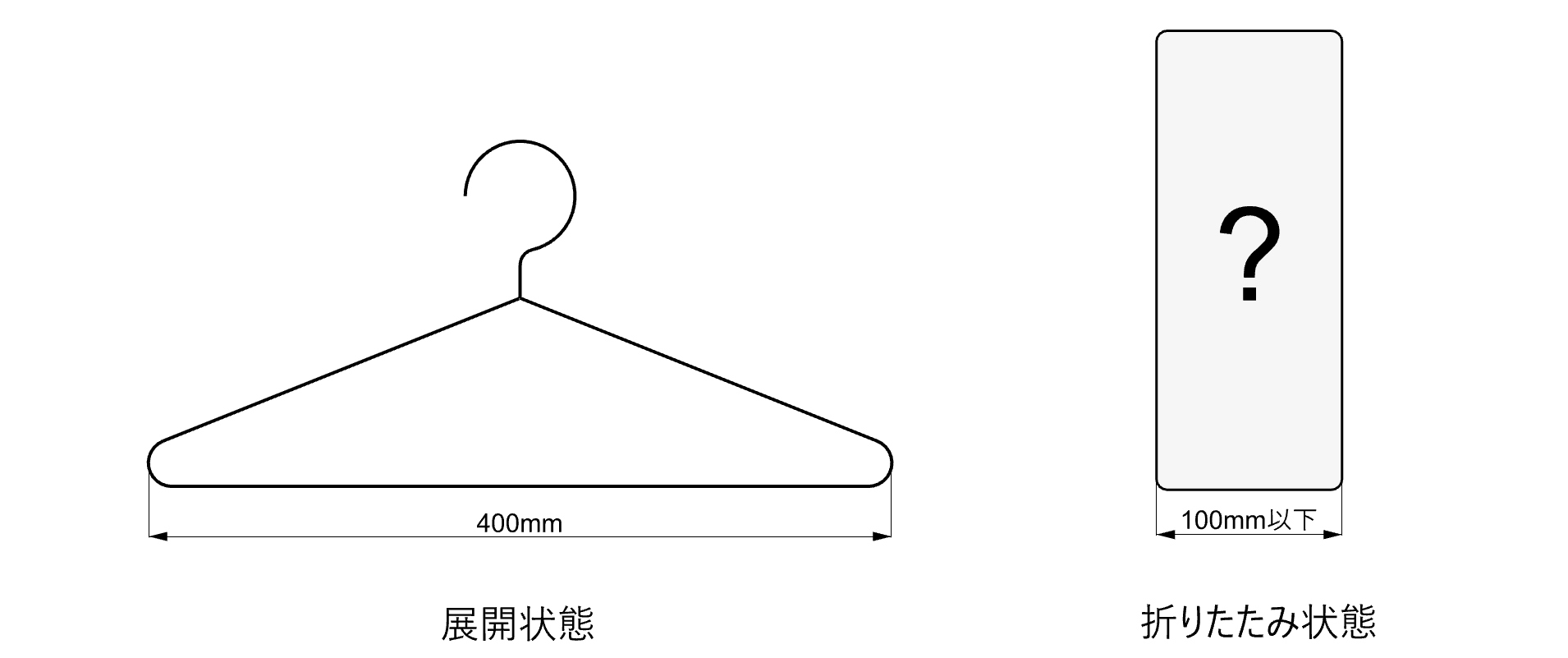
広げたときに服をかけられる形状となる
展開時横幅:400mm
折畳時横幅:100mm以下
厚み(図の奥行方向):15mm以下
折りたたみ状態 ⇨ 展開状態 遷移荷重:3N±10%
また、製造性を考慮して以下の前提を置きます。
製造制約
形状:射出成形で製造可能で、アンダーカットなしの形状とする
材質:POM M90-44 (弾性率2500MPa、ポアソン比0.35)
許容応力:31MPa(クリープ破壊寿命が10年となる応力)
機構の選択
市販の折りたたみハンガーの変形機構は様々ですが、基本的には変形しない剛体部と、回転自由度をもったヒンジ部分から構成されています。一体化するにあたっては、ヒンジをコンプライアントメカニズムで置き換える必要があります。
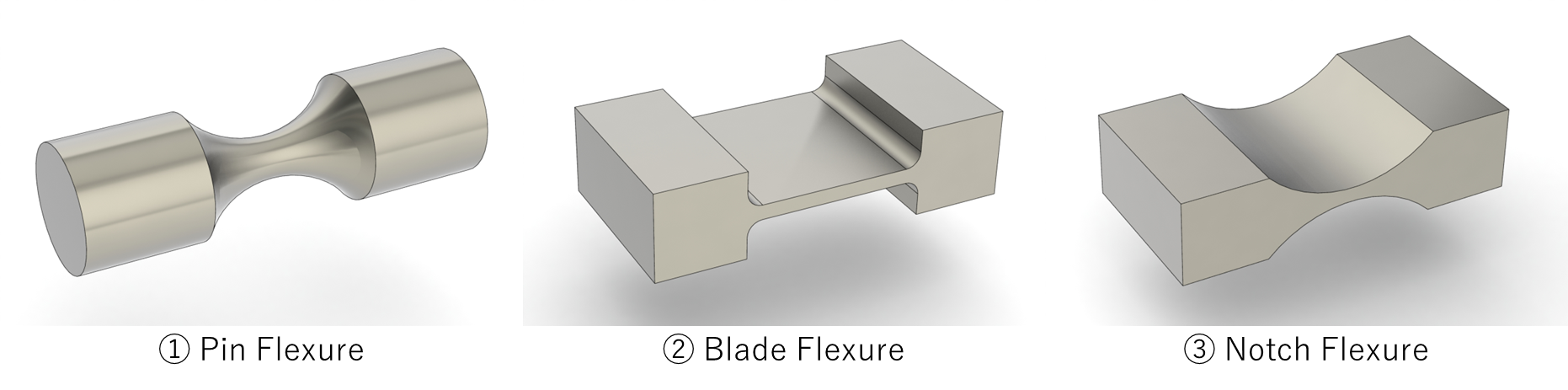
コンプライアントメカニズムのヒンジで代表的な形状には以下のような種類があり、必要な自由度や反力・製造制約などによって選択します。これらの機構を複数を組み合わせて使用することもあります。
"Pin Flexure" , "Blade Flexure" and "Notch Flexure" © 2017 OptoMechEngineer (Licensed under CC BY-SA 4.0 )
今回は、平面内の変形が必要で、必要な変形量が大きいことから、Blade Flexureを選定します。純粋にヒンジという機能を置き換えるだけであれば1軸まわり回転自由度のみを有するNotch Flexureのほうが精度に優れていますが、今回は動きの精密さよりも許容応力内での変形量が大きいことを重視し、Blade Flexureを選定しました。
また、このBlade Flexureは、0.2mm~0.4mm程度の薄さに成形しリビングヒンジとしても使用されることがありますが、今回設計する折りたたみハンガーでは、折りたたみ状態から展開状態に遷移する力を3N程度としたいので、より厚く長い寸法とし、全体を弓のようにしならせて使用することにします。
全体構成
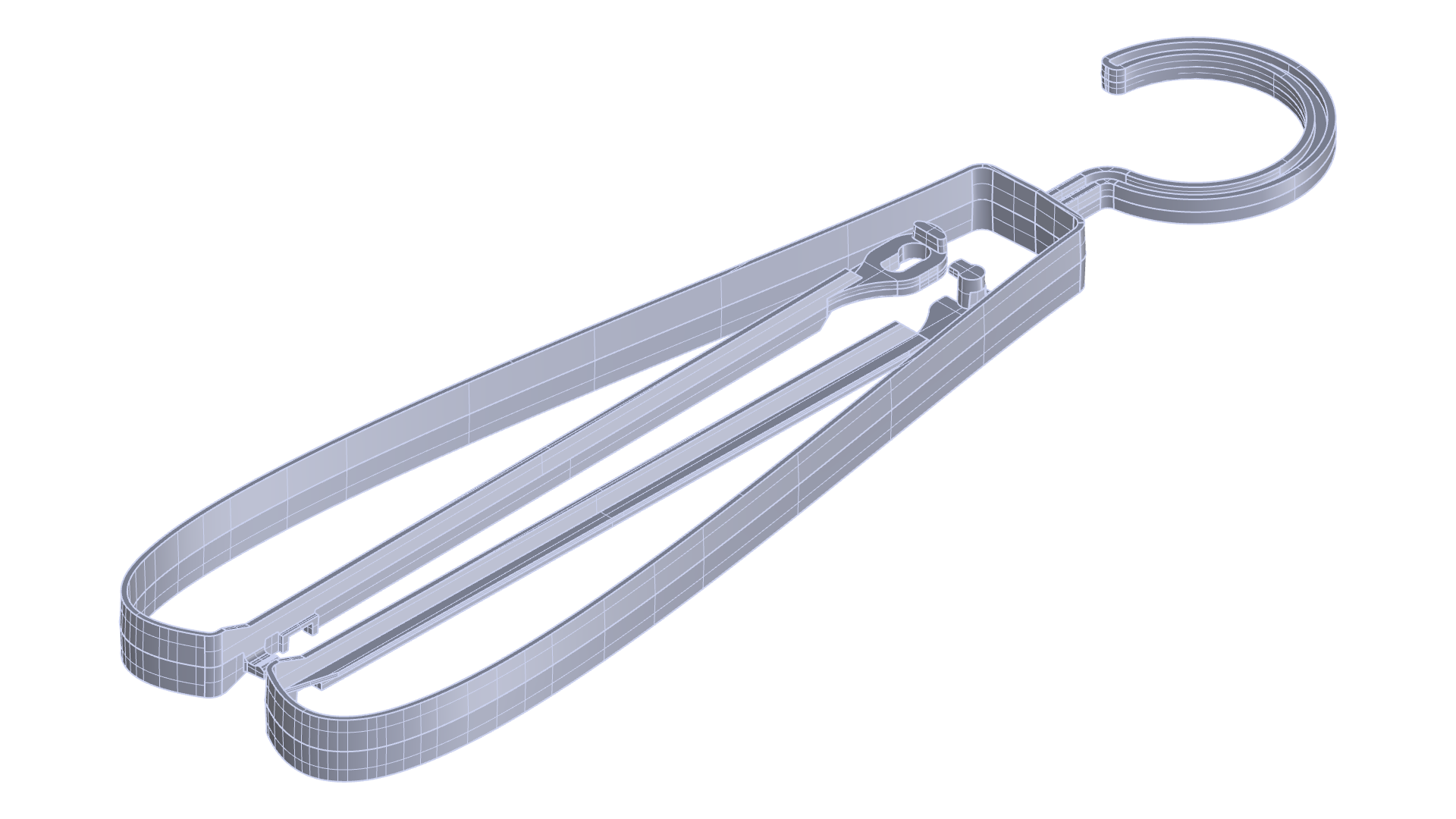
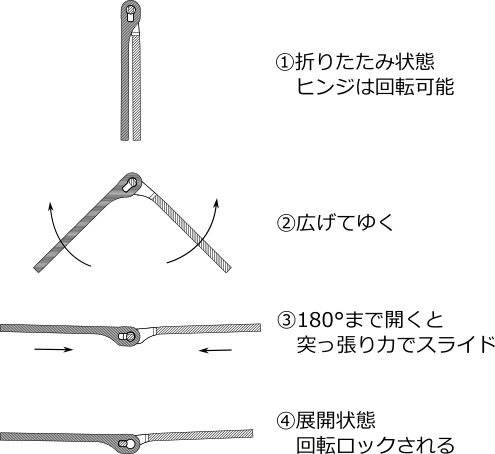
ハンガーの構成と、組み立て、開閉操作について下の図に示します。
図中左側の状態で成形したあと、「ヒンジ部」を組み立てることで「折りたたみ状態」となります。その後、ヒンジ部または直線部を手で動かすことで、折りたたみ状態と展開状態を行き来することができるようにします。
「ヒンジ部」は離型後に組み立てることでヒンジとして機能する設計とします。リビングヒンジを採用し一体成型することも考えられますが、図の前後方向の金型分割での成形が困難であることや耐久性の懸念から、今回は組み立て式ヒンジとします。
「弓部」は前述のBlade Flexureを多数連結したものとみなすことができます。ただし曲線的に連結していること、また大変形させることから、同機構が単独で本来持つ自由度の拘束は弱まっています。今回は変形量と反力、広げたときにハンガーの形状になることを重視し、このような使い方としています。
「直線部」は、ヒンジ部と弓部下端との距離を一定に保つ役割があり、ほぼ剛体として機能するよう、十分な曲げ剛性を持たせる必要があります。
独自設計環境
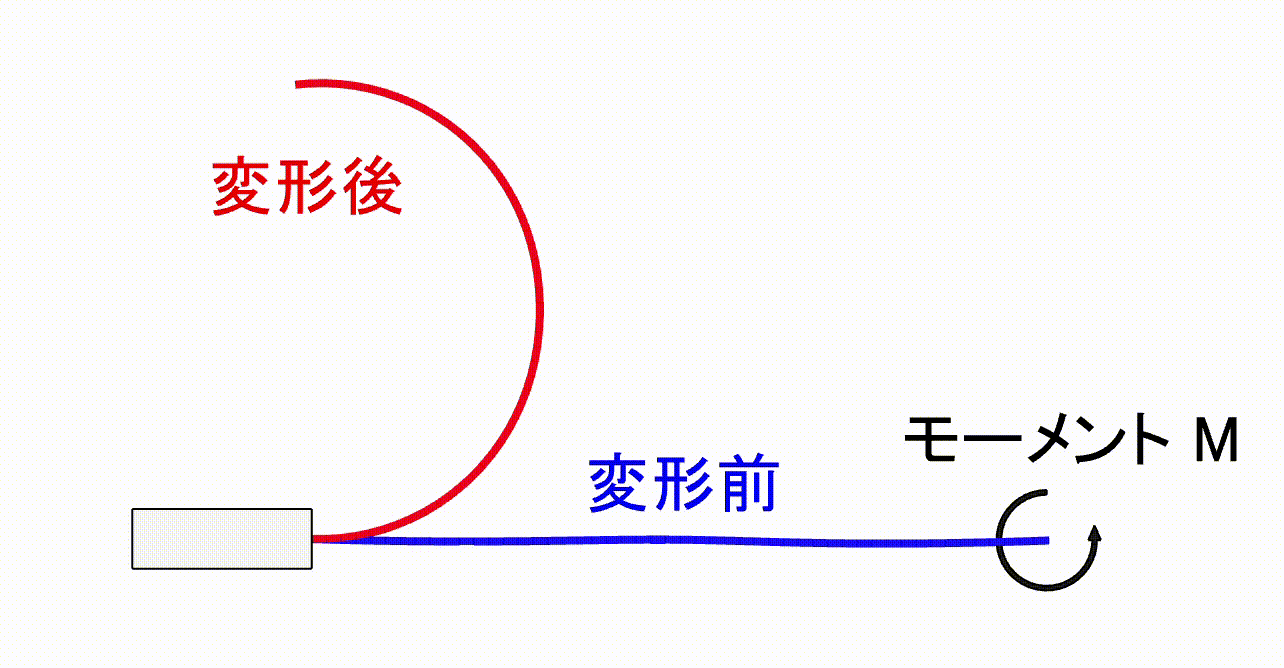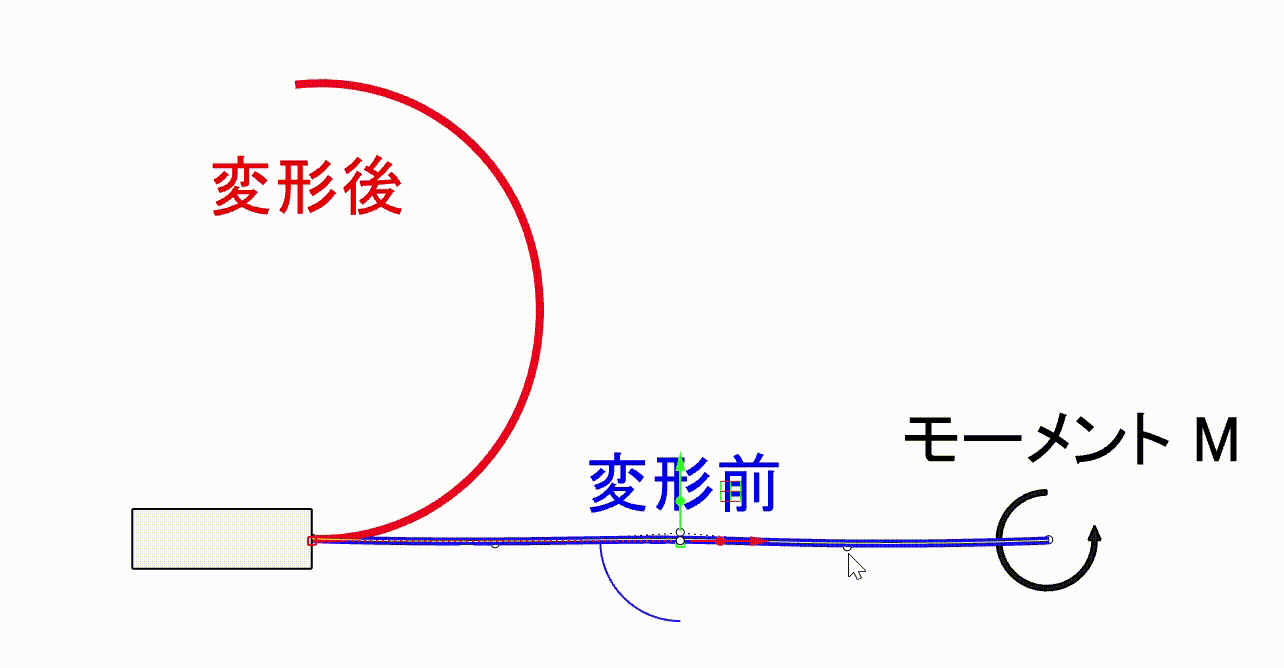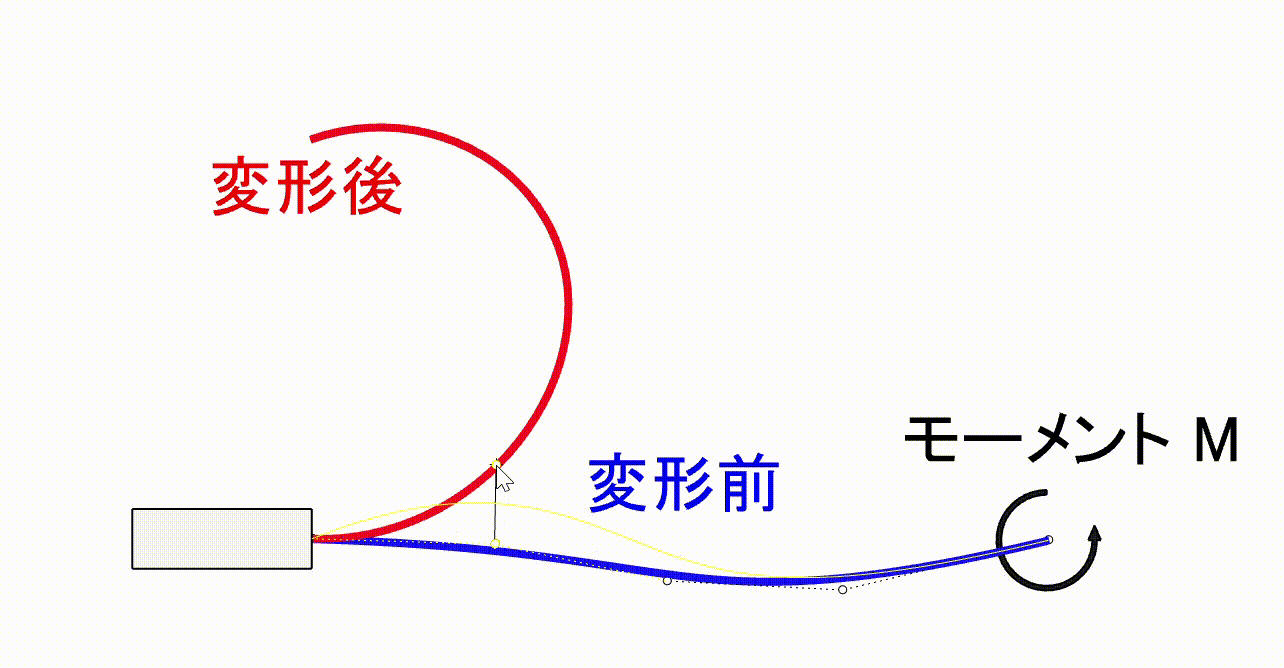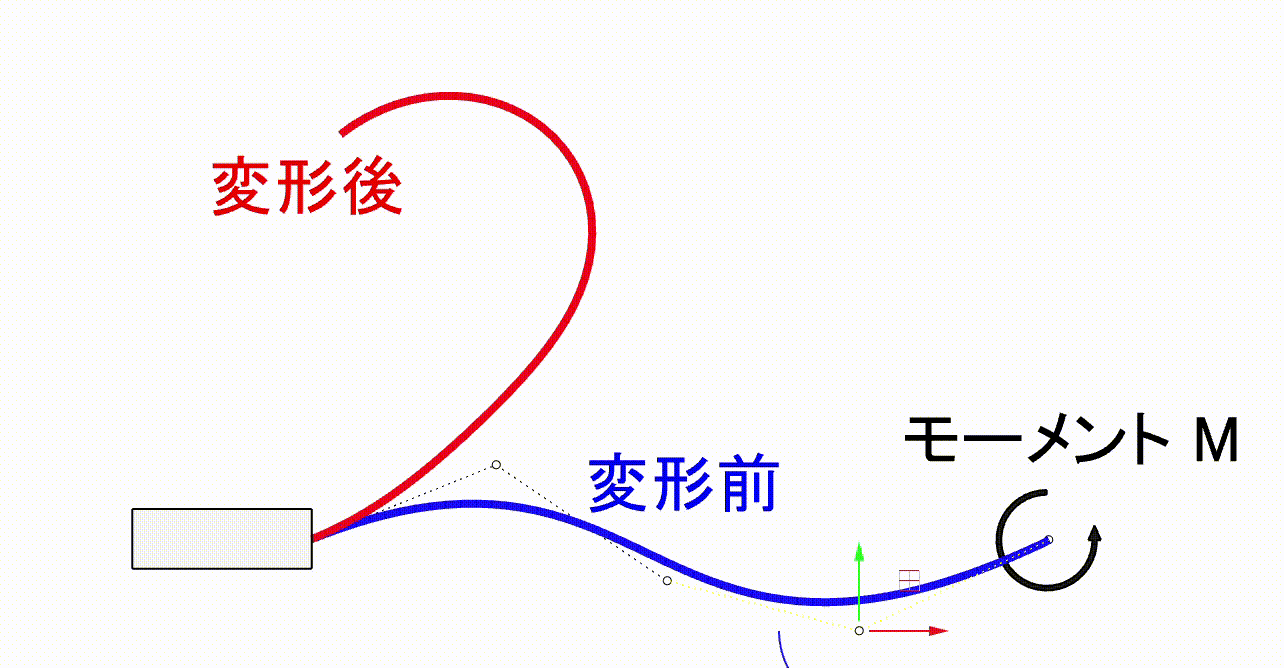
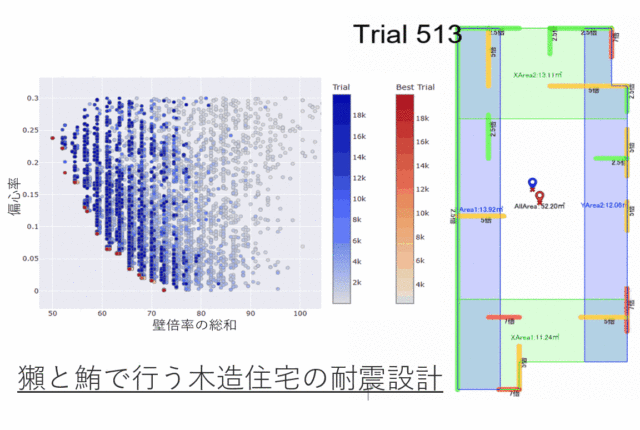
変形後にちょうどハンガーらしい形状になる曲線の梁を設計するにはどうすればよいでしょうか。リビングヒンジのように動きが単純な場合や、微小変形を仮定できる場合は比較的容易です。しかし、今回は梁の広い範囲が大きく変形するため、形状修正と解析結果の確認の多数の反復を必要とし、一般的なCAD+CAE環境では困難です。
弊社では、3DCAD RhinocerosのプラグインであるGrasshopper上で機能する様々な設計環境を独自に開発し、設計問題に応じて柔軟に使い分けています。(Grasshopperについては過去の記事 で詳しく紹介しています。)
今回は、梁を2次元梁要素でモデル化し変形をリアルタイムで確認しながら設計を行える環境を使用します。この環境を活用することで、多数の形状を短時間で検証することができ、目的の変形をする機構を効率よく探索することができます。
形状検討
上記ツールを活用して、弓部および直線部の形状を具体化していきます。
まず解析の設定をして、成形時の形状をモデリングすれば即座に解析が走り、
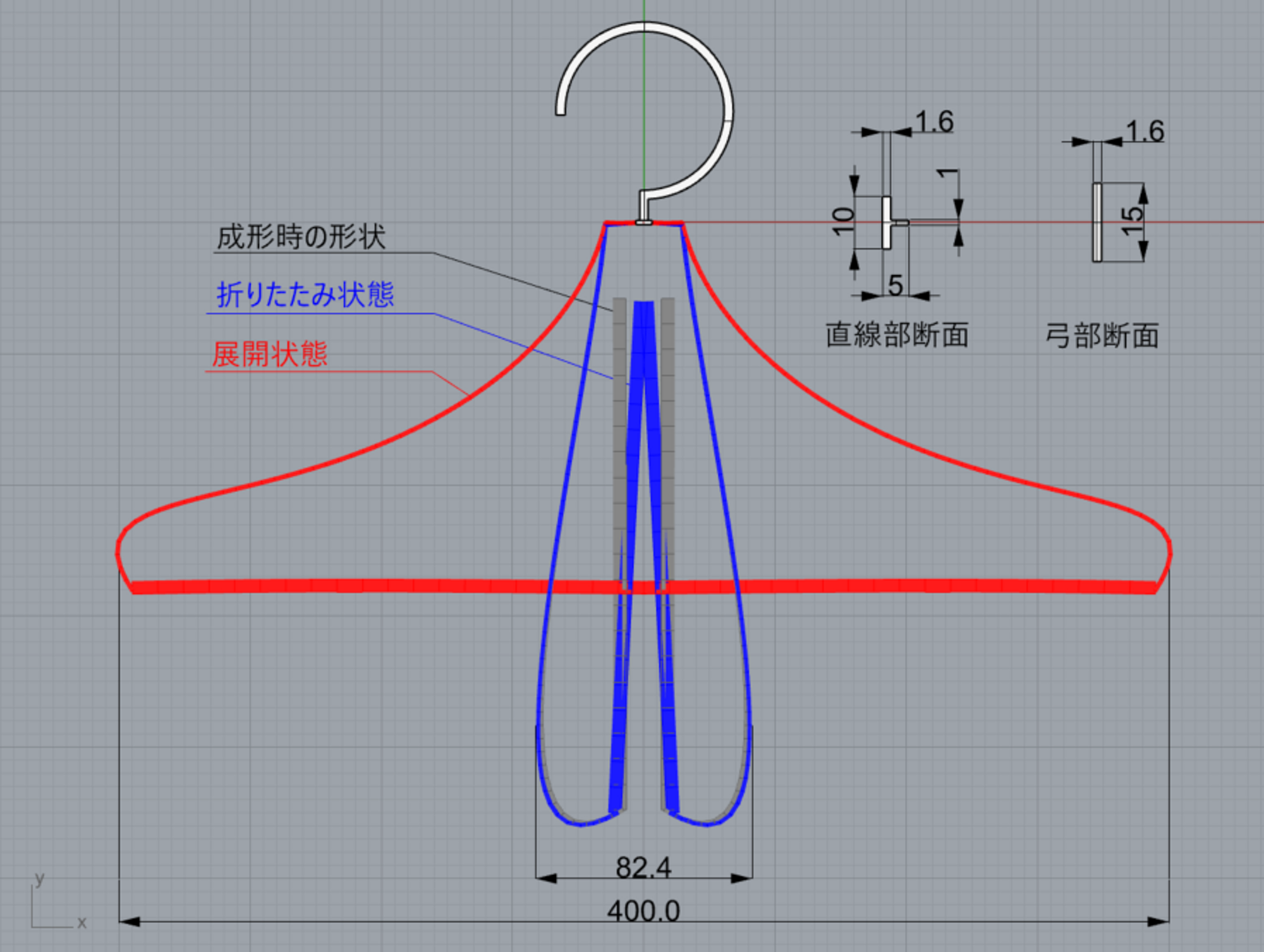
折りたたみ状態と展開状態の形状
変形に要する力
途中の最大応力
が確認できる状態にします。このときの境界条件は、フック部の付け根を固定とし、ヒンジ部は最初にX方向の変位を与えて組立状態にし、続いてY方向の変位を与えて展開状態まで変形させています。
上の3項目確認しながら探索した結果、下の図の形状で要件を満たすことが確認できました。展開状態の形状はハンガーらしい形状で良好です。
弓部の断面形状は、曲げ方向に薄い長方形として曲げたい方向の剛性を下げ、同時に展開操作の操作力と最大応力が狙いの値となるよう寸法を調整しています。直線部は高めの剛性が必要なため、初期的には比較的厚い3.5mm×10mmの長方形としましたが、第2部で述べる成形性の検討から最終的には図に示すT字形状としました。
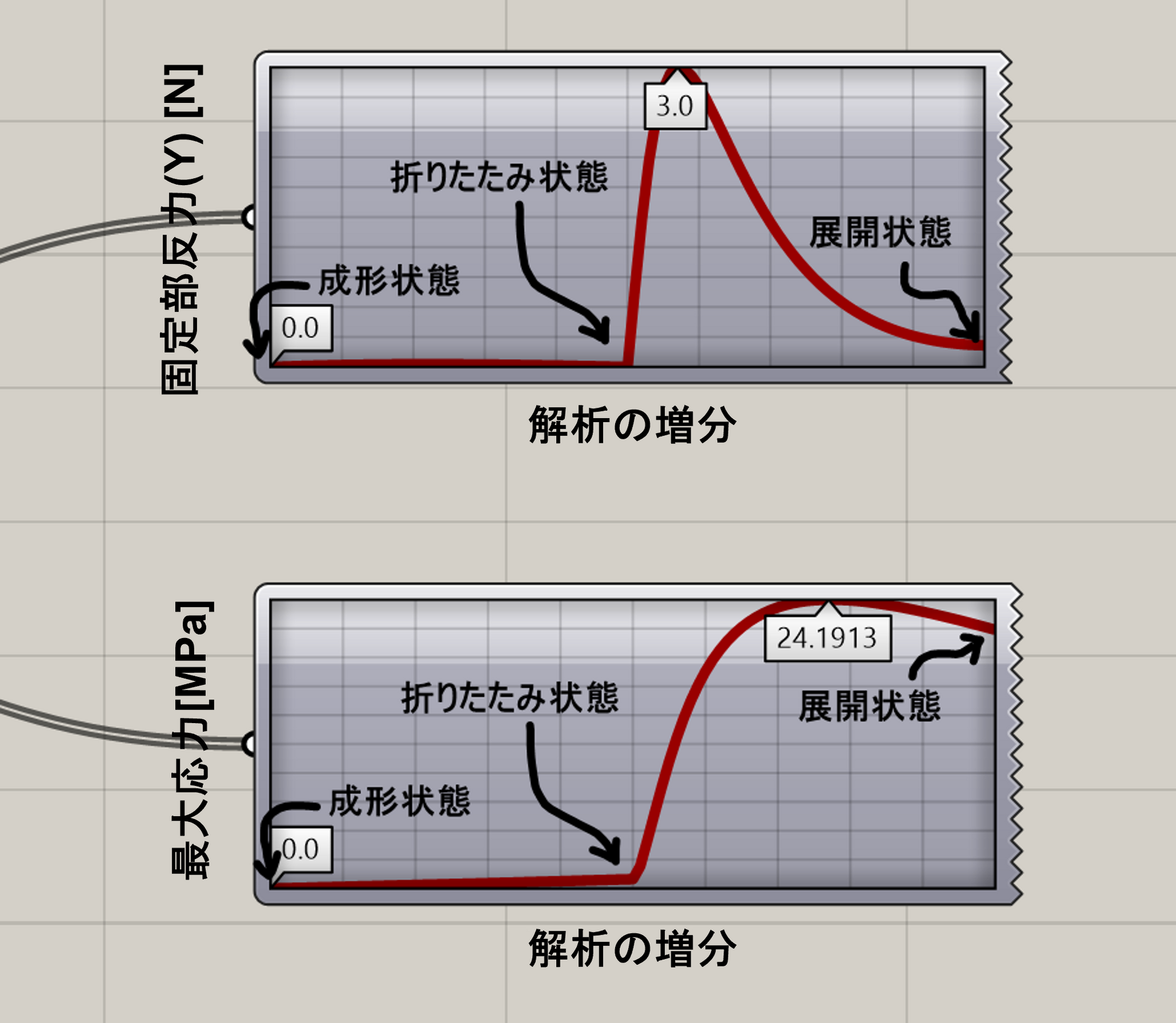
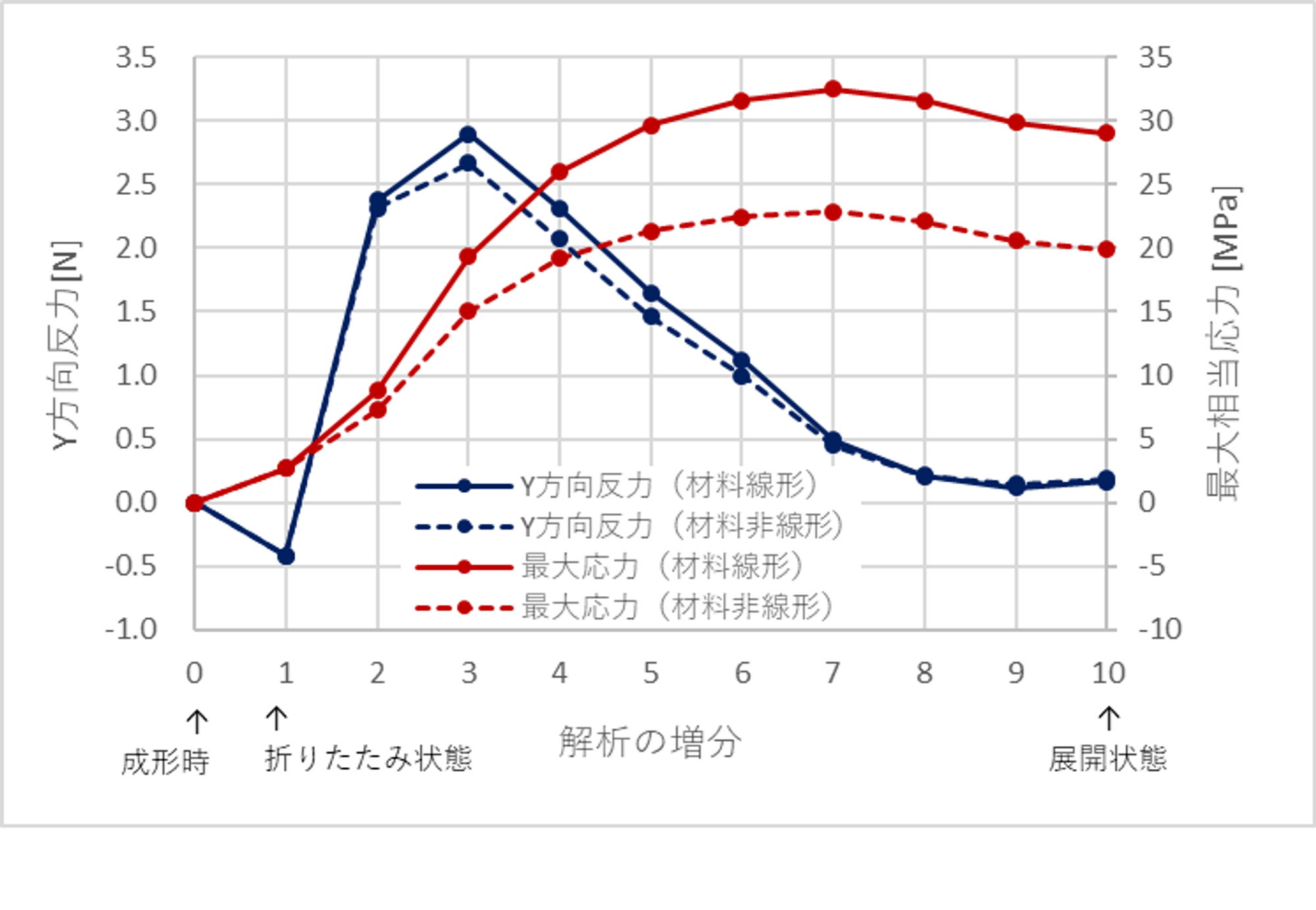
解析における各変形段階の応力と固定部反力(=操作に必要な力)は以下のようになりました。最大値は冒頭で設定した要件(それぞれ3N±10%、31MPa以下)を満たしていることが確認できます。
詳細設計
直線部および弓部の形状と断面が決定されたので、詳細設計に進みます。ロック機能のあるヒンジ部、クリープ対策のため閉じた状態で固定できる爪、フック部の肉抜き、抜き勾配などを考慮し、下の形状となりました。成形性を考慮しアンダーカット部が発生しない形状としています。フック部肉抜きについては第2部で詳しく述べます。
下の断面図に示すように、ヒンジ部は展開すると軸がスライドし、回転がロックされる機構としました。
詳細解析による性能確認
次に詳細設計の3Dデータをもとに、一般的なCAEソフトウェアでソリッド要素での構造解析を行い、応力および反力の確認を行います。境界条件として、フック部付け根を固定し、ヒンジ部の軸および穴部に変位を与えることで、成形時の形状 ⇨ 折りたたみ状態 ⇨ 展開状態 の動きを再現します。
解析の結果、Grasshopper上でのシミュレーションどおり、展開時にハンガー形状となること、反力が3N程度となることが確認できました。最大応力についてはgrasshopper上でのシミュレーションでは24.2MPaでしたが、ソリッド要素での解析では材料線形で32.5MPa(グラフの赤実線)となり、差が出ました。前者は梁要素における最大応力であったため、抜き勾配やRが小さい箇所の応力集中が反映されておらずこのような差が生じていると考えられます。
上記の通り、材料線形の計算結果では最大応力が当初想定した許容応力31MPaを超えてしまっていますが、この応力水準では材料の非線形性の影響が小さくありません。材料非線形で解析した結果、最大応力は22.8MPa(グラフの赤破線)となり許容応力以下であるため問題ないと判断しました。
簡易モデルで設計検討を行う際は、解析モデルの忠実度に応じて目標値のマージンを確保しておくことが重要です。今回の事例では、形状を忠実にしたことによる応力の上昇と、材料を忠実にしたことによる応力低下が打ち消し合う結果となりました。
試作
最後に3Dプリンタを使用して試作し、想定通り機能することを確認しました。冒頭の動画をご覧ください。
なお材質をPOMではなくPLAでプリントしたため、状態が遷移する際の反力は設計値よりも低くなっています。
さいごに
本記事では、コンプライアントメカニズムを活用した複数部品の一体化の事例として、折りたたみハンガーの設計について紹介しました。設計の考え方やコンプライアントメカニズムの可能性について感じていただけていれば嬉しいです。
次回は成形性についてより詳しく解説した記事を公開予定です。




 Created by modifying
Created by modifying