はじめに

 この記事をお読みの皆さんは，日頃からヒンジキャップに弾性エネルギーを蓄えては解放し，解放しては蓄えていることと思います。

 双安定性を有するヒンジキャップは，開いた状態と閉じた状態のどちらでも停止することができます。このように2つの異なる安定状態（すなわち双安定性）を有する構造を双安定構造(Bistable Structure)と言います。双安定ヒンジキャップは代表的なコンプライアントメカニズム応用例のひとつです。  本記事では，双安定構造の観点からヒンジキャップを観察した内容を記します。

ヒンジキャップ

 ヒンジキャップにはいくつか種類があります。今回は100円ショップで購入した3種類（一般的な名称が存在しないため造語を含めています）のヒンジキャップについて紹介します。

L字型ヒンジ (L-shaped Hinge)

 中央部のL字部材（下図の赤点線）が変形することで復元力を生み出しています。 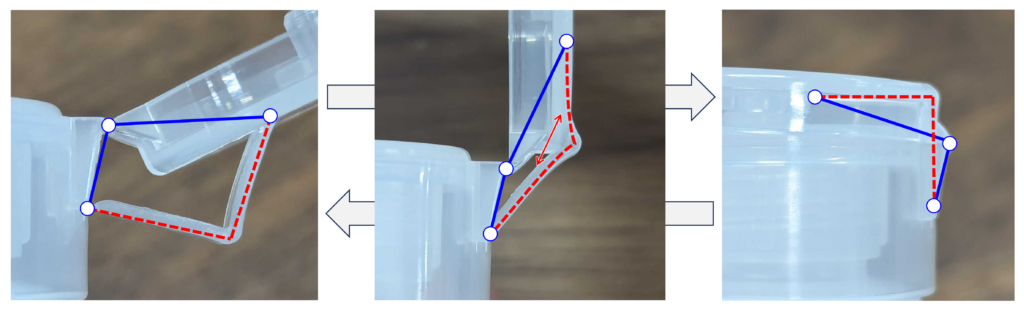左右の画像は安定した状態を示し，中央の画像は開いた状態から閉じた状態（もしくは逆）へ遷移する途中の不安定な状態を示しています。

 青い実線で示す剛ヒンジが直線となる（蓋が90°開いた）状態から，内側に曲がれば閉じる方向へ，外側に曲がれば開く方向へ遷移します。このとき，赤い線で示すL字部材が90°なると復元力がなくなり安定します。中央の遷移状態を蓋が90°開いたときとするため，閉じた状態でもヒンジが蓋の外に位置し凸部を有する形状となります。

 単純な機構なので反力や開き角度の調整が容易です。また，他の種類に比べてヒンジ寸法が大きいためモーメント反力を大きくできるという特徴があります。

横梁型ヒンジ (Side-beam Hinge)

 中央部がフラットなヒンジ（下図の青実線）になっており，両側についている細い梁（下図の赤点線）が変形することで復元力を生み出しています。 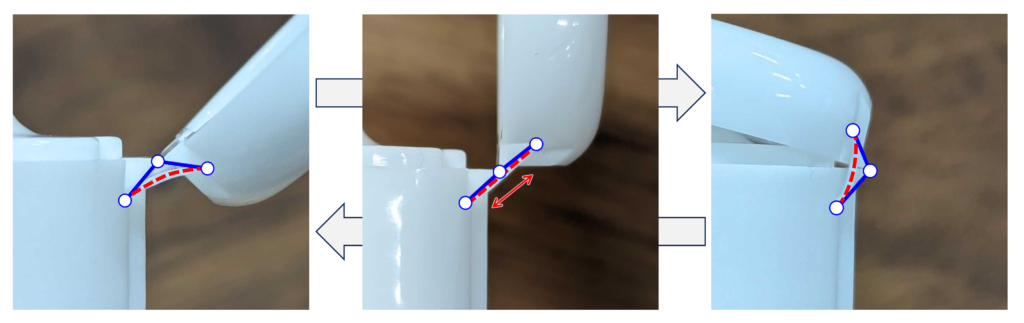中央の状態では，赤点線で示す梁が伸びて不安定となっています。青色で示すヒンジの角度によってどちらかに倒れ，赤点線で示す梁の引張と曲げによる復元力がつり合う状態で安定します。

 上述のL字型よりもヒンジ部がコンパクトになっており外観が目立ちません。フラットヒンジを設けるために蓋が円形から削れた形状になっています。

 また，梁軸方向の伸びを利用するため高い応力が発生し，3種類の中では最も耐久性が低い構造と考えられます。

バタフライヒンジ (Butterfly Hinge)

 複曲面が裏返ることで双安定性を生み出しています。 中央の図で示すように，蓋が90°開いた遷移状態ではヒンジが平面に近い状態となります。このとき，側部が伸びることで復元力が生じます。

 側部の引張による復元力を利用しているため，上述の横梁型のヒンジを連続的につなげたとも言えます。大きなフラット部分を設ける必要がなく蓋を円形に保ちやすいという特徴があります。広い範囲で荷重を受けているため，横梁型に比べて反力を大きくできること，また耐久性を高くできることがメリットと考えられます。

 複曲面構造では，曲げ剛性による復元力よりも面内剛性による復元力が大きい場合，両者が釣り合うときに安定状態となります。ヒンジキャップではガウス曲率が正の複曲面を使用していますが，ガウス曲率が負の曲面を使っても双安定構造になりえます。しかし，遷移状態において側部が圧縮荷重を受け座屈を生じうる，閉じた際に円形状に沿わないといった理由から，ヒンジキャップには用いられていないものと考えられます。

もう少し詳しく

 上記までには数式がなくて寂しいので，簡単なモデルを用いてパラメータによる特徴を調べてみましょう。

 双安定ヒンジを単純化すると、図のようなバネリンク機構で考えられます。 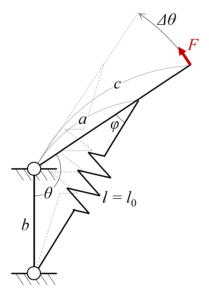バネ部の長さは初期状態（安定状態）においてl=l_0とします。

荷重がかかる剛リンクが角度θにあるとき，バネの長さlは

l=\sqrt{a^2+b^2-2ab\cos\theta}

となります。このとき，回転方向に必要な荷重Fおよび，バネに蓄えられる弾性エネルギーEは次のようになります。

F=k(l-l_0)\sin\phi\cdot\frac{a}{c}=\frac{kab}{c}(1-l_0/l)\sin\theta\\
E=\frac{1}{2}k(l-l_0)^2

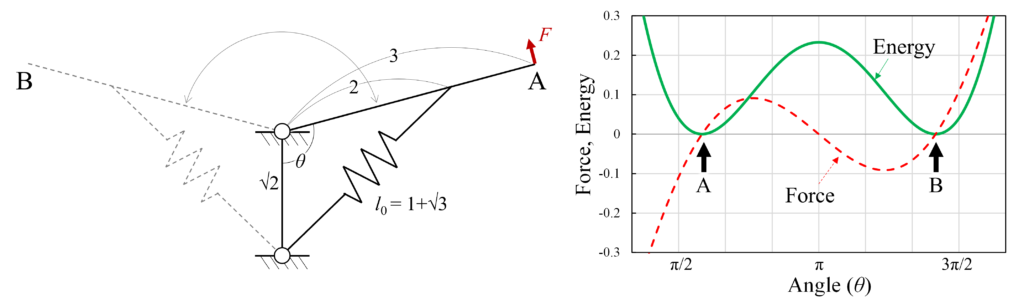
 例えば，a=2,b=\sqrt{2},c=3,l_0=1+\sqrt{3}(\theta_0=\frac{7}{12}\pi)のとき，荷重およびエネルギーは次の右図のようになります。左図の安定状態は，弾性エネルギーが極小値をとる点での形状となります。  このように，双安定構造ではポテンシャルエネルギー（ここでは弾性エネルギー）が極小値を2つ持ちます。極小値において安定状態となり，極大値を乗り越える十分な外力が与えられるともう一方の安定状態に遷移することができます。すなわち，極大値が大きいほど遷移するためにより大きな外力を必要とし安定状態を保ちやすいと言えます。

 今回のバネヒンジモデルにおいて，初期角度\theta_0および負荷部分までの距離cが決定している場合を考えます。このとき，弾性エネルギーは\theta＝\piで極大となり,極大値E_{LM}は次のようになります。

E_{LM}=\frac{1}{2}k(a+b-\sqrt{a^2+b^2-2ab\cos\theta_0})^2

括弧内をaで微分すると

\frac{d}{da}\left(a+b-\sqrt{a^2+b^2-2ab\cos\theta_0}\right) = 1+\frac{b\cos\theta_0-a}{\sqrt{a^2+b^2-2ab\cos\theta_0}}

ここで，\theta \ne 0,\piとすると第2項目は

\left(\frac{b\cos\theta_0-a}{\sqrt{a^2+b^2-2ab\cos\theta_0}}\right)^2
=1-\frac{b^2(1-\cos^2\theta_0)}{a^2+b^2-2ab\cos\theta_0}
<1 \\
-1<\frac{b\cos\theta_0-a}{\sqrt{a^2+b^2-2ab\cos\theta_0}}<1

となるため，\frac{dE_{LM}}{da}は常に正でありE_{LM}はaに対して単調増加であることが分かります。対称式なので同様にbに対しても単調増加となります。これにより，aとbの寸法は大きいほどエネルギー極大値が大きく，より安定的することが分かります。ただし，現実にはヒンジ部に利用できるスペースが有限であることと，バネ部材を長くすると剛性（バネ定数）が小さくなることから，適切な寸法が決まってくるものと考えられます。

 また，バネ部材の初期長さl_0も一定のときは，荷重とエネルギーともにa=bのときに極大値が最大となります。参考までに下図にaとbを変えたときの荷重とエネルギーのグラフを示します。

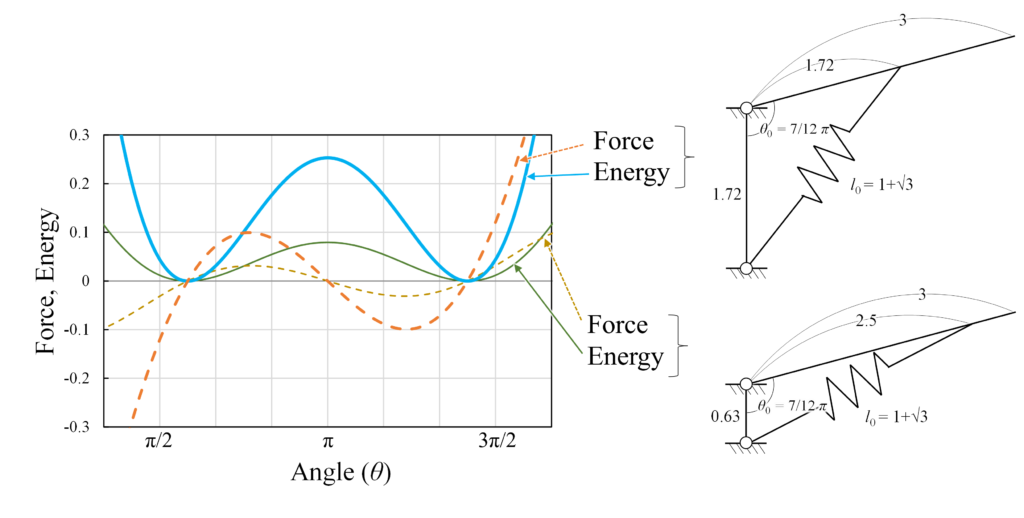
 このように，より安定的な双安定構造を設計するためには，剛ヒンジ部の長さ(a,b)をできるだけ同じ寸法で大きくすれば良いことが分かります。最初に紹介したL字型ヒンジではaとbの長さが異なりますが，スペース制約によるものと思われます。

まとめ

 双安定ヒンジキャップについて解説しました。これからもヒンジキャップを見かけたときは，弾性エネルギーの変化に思いを馳せながら，その動きを楽しんでみてください。