はじめに
以下の動画で紹介しました、防振構造において課題となるサージングを構造により解決したダンパーレス*バネの設計に関して、2部構成で技術的な解説をします。
*「ダンパーレス」は弊社の商標です。
サージングとは
様々な分野でサージ・サージングというワードが使われますが、本記事では防振構造の固有振動をサージングと表現します。
サージングは防振構造の防振可能周波数帯を決める一因となります。
一般に、振動系の1次共振周波数f_1は防振構造の剛性kとマウント物の質量mにより決まり、周波数fがf_1で振動伝達率T_rが極大をとり、\sqrt{2}f_1を超えると振動伝達率が1を下回ります。
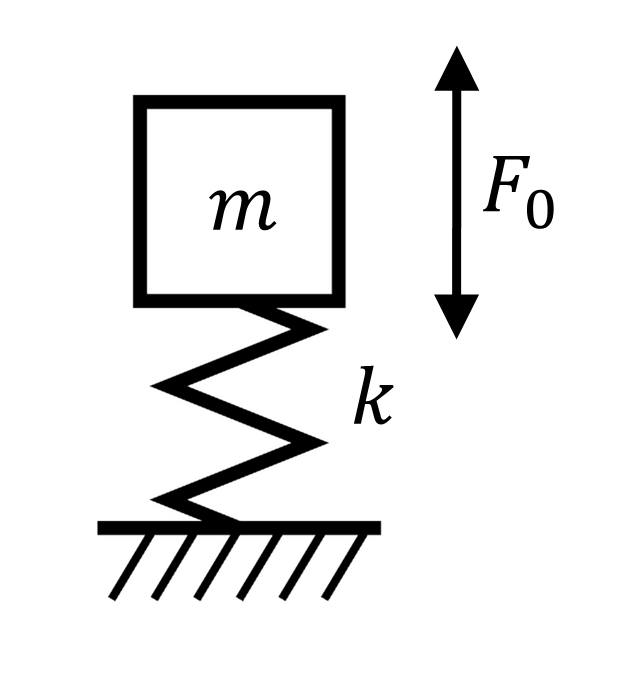
1自由度のばねマス系において、振動伝達率T_rは以下のように導かれます。(導出は別の記事で紹介しております)
\begin{align}
f_1&=\frac{1}{2\pi}\sqrt{\frac{k}{m}}
\tag{1-1}
\\
T_r&=\left|\frac{f_1^2}{f_1^2-f^2}\right|
\tag{1-2}
\end{align}この式では、f_1以降周波数が大きくなるにつれ振動伝達率が下がり続けますが、現実にはばねの質量による共振で振動伝達率は上昇します。
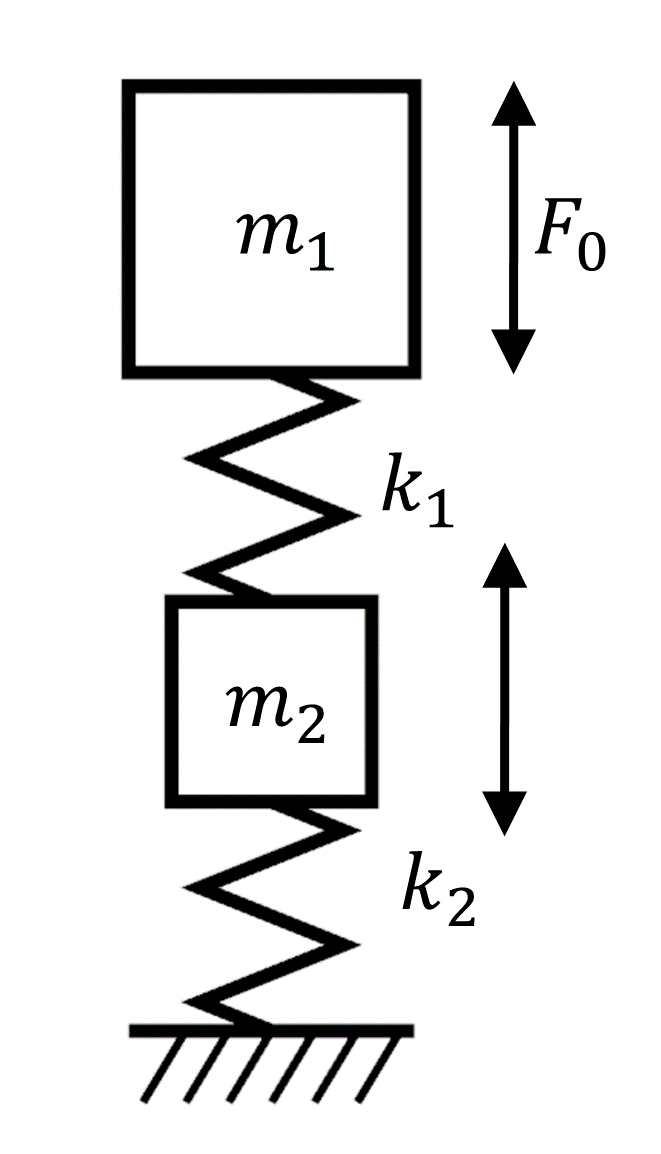
質量m_1-ばねk_1-質量m_2-ばねk_2の順に並んだ2自由度のばねマス系において、振動伝達率T_rは以下のように導かれます。
\begin{gather}
\omega=2\pi f
\tag{1-3}
\\
T_r=\left|\frac{k_1k_2}{(-m_1\omega^2+k_1)(-m_2\omega^2+k_1+k_2)-k_1^2}\right|
\tag{1-4}
\end{gather}m=m_1=1、m_2=0.1、k=50000、k_1=k_2=100000で振動伝達率をプロットすると以下のようになります。
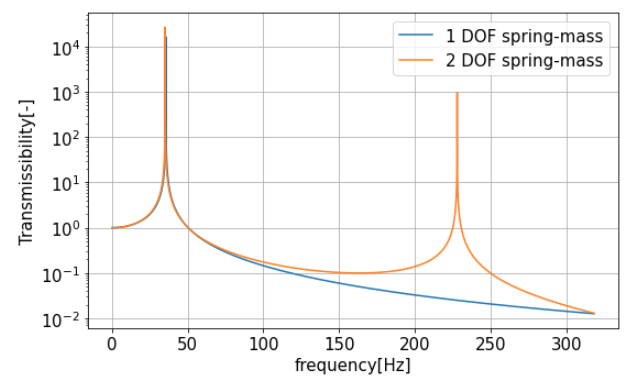
m_2をばねの質量と解釈すれば、ばねの質量とその運動による固有振動によって共振周波数が増えているといえます。
実際のばねは連続的に質量が分布しており、理論上は無限個の共振周波数が存在します。
このように防振構造のサージングにより振動伝達率が増大し、防振可能な周波数帯が限られたものになります。
サージングの影響を軽減するためにダンパー(減衰機構)や減衰の大きな材料がよく使われています。
梁におけるサージング
連続体におけるサージングの例として、厚みが一様な梁におけるサージングを共振周波数の導出を交えながらみていきます。
また、形状により共振周波数を上げることができることもみていきます。
直線の梁におけるサージング
以下のような両端が固定された長さ\ellの直線の梁を考えます。
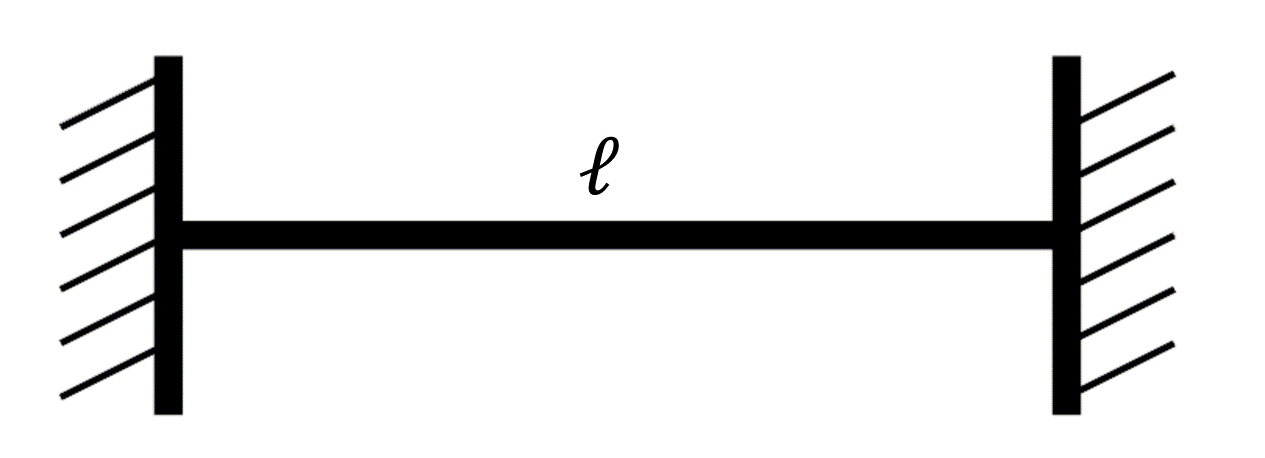
梁理論における以下の運動方程式から固有振動を起こす周波数(共振周波数)を導出します。
EI\frac{\partial^4 u}{\partial x^4}+\rho A\frac{\partial^4 u}{\partial t^2}=0
\tag{2-1}ここで、ヤング率E、断面二次モーメントI、密度\rho、梁断面積A、梁の長手方向にとった座標 x、梁の長手方向および奥行き方向に垂直な変位uと文字を定義しました。
時間tに関する周期性を仮定し、u=U(x)\exp(i\omega t)と変数分離することで以下の一般解が得られます。
\begin{gather}
u=\left(C_{1}\cosh\frac{\lambda x}{\ell} + C_{2}\cos\frac{\lambda x}{\ell} + C_{3}\sinh\frac{\lambda x}{\ell} + C_{4}\sin\frac{\lambda x}{\ell}\right)\exp(i\omega t)
\tag{2-2}
\\
\lambda_1^4=\frac{\omega^2\ell^4\rho A}{EI}
\tag{2-3}
\end{gather}両端固定の束縛条件から係数C_1、C_2、C_3、C_4は以下の式を満たします。
\begin{gather}
C_1+C_2=0
\tag{2-4}
\\
C_3+C_4=0
\tag{2-5}
\\
C_{1}\cosh\lambda + C_{2}\cos\lambda + C_{3}\sinh\lambda + C_{4}\sin\lambda=0
\tag{2-6}
\\
C_{1}\sinh\lambda - C_{2}\sin\lambda + C_{3}\cosh\lambda + C_{4}\cos\lambda=0
\tag{2-7}
\end{gather}この連立方程式の解としてC_1=C_2=C_3=C_4=0がありますが、この解は振動しない状況です。
C_1=C_2=C_3=C_4=0以外の解を持つには、上記連立方程式の係数行列の行列式がゼロになる必要があります。
この条件から以下の式が得られます。
\cos\lambda \cosh\lambda-1 = 0
\tag{2-8}\lambdaについて数値的に解くと、\lambda_i=4.73, 7.85, 11.0, \cdotsと得られます。
この\lambda_iを用いて共振周波数f_iは以下のように求まります。
f_i=\frac{1}{2\pi}\frac{\lambda_i^2}{\ell^2}\sqrt{\frac{EI}{\rho A}}
\tag{2-9}このように梁理論による運動方程式をもとに、波が安定して存在するという条件から共振周波数を見積もることができます。
この梁構造をそのまま防振構造として使用した場合、梁構造の共振周波数近傍において振動伝達率が大きくなります。
曲がった梁におけるサージング
以下のような両端が固定された、長さ\ell_1,\ell_2の2本の直線の梁からなる折れ曲がった梁構造を考えます。
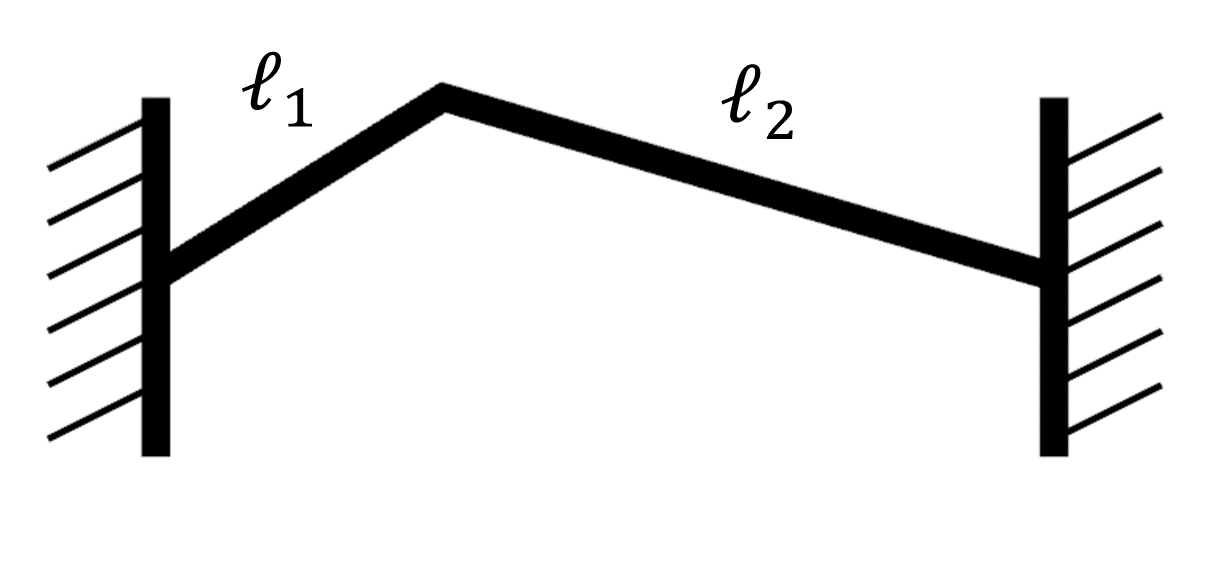
それぞれの梁の伸びる方向に沿ってx,y座標をとり、それぞれx,y方向および奥行き方向に垂直な変位をu,vとおくと以下のように運動方程式がたてられます。
\begin{align}
EI\frac{\partial^4 u}{\partial x^4}+\rho A\frac{\partial^4 u}{\partial t^2}&=0
\tag{2-10}
\\
EI\frac{\partial^4 v}{\partial y^4}+\rho A\frac{\partial^4 v}{\partial t^2}&=0
\tag{2-11}
\end{align}2本の梁両方で前述した直線梁と同じ変位の一般解が得られます。
\begin{gather}
u=\left[C_{11}\cosh\frac{\lambda_1 x}{\ell_1} + C_{21}\cos\frac{\lambda_1 x}{\ell_1} + C_{31}\sinh\frac{\lambda_1 x}{\ell_1} + C_{41}\sin\frac{\lambda_1 x}{\ell_1}\right]\exp(i\omega t)
\tag{2-12}
\\
v=\left[C_{12}\cosh\frac{\lambda_2 y}{\ell_2} + C_{22}\cos\frac{\lambda_2 y}{\ell_2} + C_{32}\sinh\frac{\lambda_2 y}{\ell_2} + C_{42}\sin\frac{\lambda_2 y}{\ell_2}\right]\exp(i\omega t)
\tag{2-13}
\\
\lambda_1^4=\frac{\omega^2 \ell_1^4 \rho A}{EI}
\tag{2-14}
\\
\lambda_2^4=\frac{\omega^2 \ell_2^4 \rho A}{EI}
\tag{2-15}
\end{gather}2本の梁は梁の長手方向には十分固く変形しないとすれば、幾何的な束縛から梁の結合部は並進変位をおこさず回転変位のみをおこすことになります(※2本の梁が一直線上になっている、または一直線上に近い状況ではこの仮定は成り立たないことに注意)。
両端の固定境界および梁の結合部が並進変位はせず回転変位が連続となる境界条件のもと、上記直線梁と同様に連立方程式を立て係数行列の行列式がゼロとなる条件から以下の式が得られます。
\begin{gather}
(\cosh\lambda_1\cos\lambda_1-1)(\cosh\alpha\lambda_1\sin\alpha\lambda_1-\sinh\alpha\lambda_1\cos\alpha\lambda_1)
\hspace{100pt}
\\
+(\cosh\alpha\lambda_1\cos\alpha\lambda_1-1)(\cosh\lambda_1\sin\lambda_1-\sinh\lambda_1\cos\lambda_1)=0
\tag{2-16}
\\
\alpha=\frac{\lambda_2}{\lambda_1}=\frac{\ell_2}{\ell_1}
\tag{2-17}
\end{gather}ここで、\alphaは構造から決まるパラメータであり、0<\ell_2\leq\ell_1としても一般性を損ねないため、0<\alpha\leq 1とできます。
\lambda_1は\alphaに対して以下のように数値的に求められます。
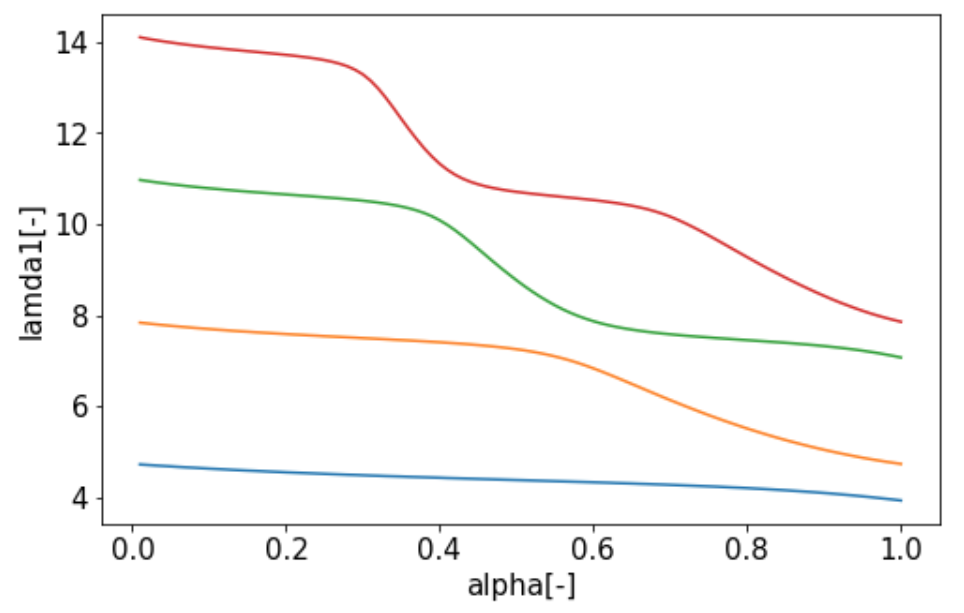
この求まった\lambda_{1i}から共振周波数f_iは以下のように書かれます。
f_i=\frac{1}{2\pi}\frac{\lambda_{1i}^2(\alpha)}{\ell_1^2}\sqrt{\frac{EI}{\rho A}}
\tag{2-18}直線梁と曲がった梁の共振周波数の比較
直線梁と曲がった梁の共振周波数を比較するために、直線の梁を中心で曲げた構造を考えます。
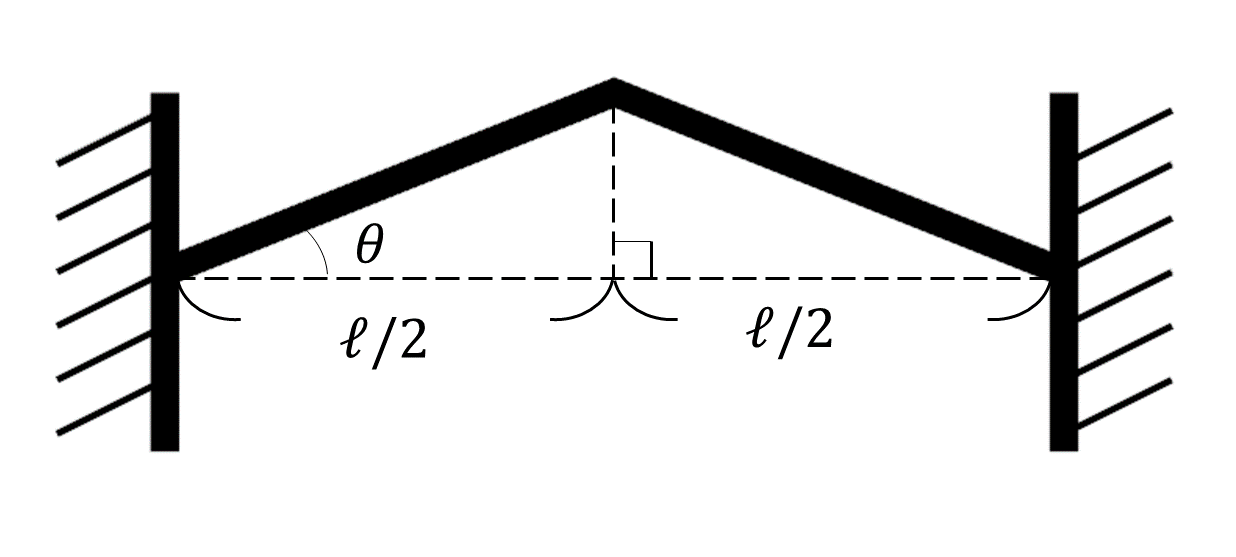
両端の距離は\ellで一定として、曲げの角度\thetaを振ったときの1次の共振周波数の変化を比較します。
上記で導出した解析解と梁要素によるシミュレーション結果を、以下の通り表とグラフにまとめました。
角度\theta [°] |
共振周波数f_1【解析解】[Hz] |
共振周波数f_1【シミュレーション】[Hz] |
|---|---|---|
| 0 | 340(直線梁) | 339 |
| 5 | 929 | 745 |
| 10 | 908 | 902 |
| 15 | 873 | 868 |
| 20 | 826 | 822 |
| 30 | 702 | 698 |
| 40 | 549 | 547 |
| 50 | 387 | 385 |
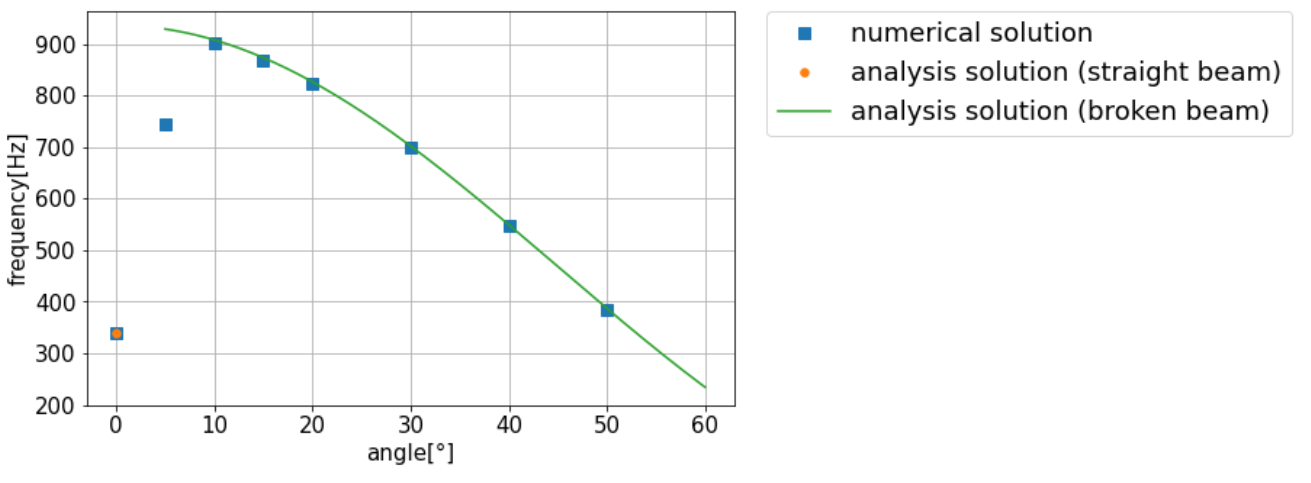
ここで、ヤング率E=3\rm{GPa}、密度\rho=1100\rm{kg/m^3}、長さ\ell=0.1\rm{m}とし、梁断面は長方形断面(奥行き0.01\rm{m}、高さ0.002\rm{m}、断面積A=0.00002\rm{m^2}、断面二次モーメントI\simeq6.67\times10^{-12}\rm{m^4})としました。
また、\theta=0°のときは直線の梁(straight beam)の解析解を使い、それ以外は曲がった梁(broken beam)の解析解を使用しました。
表およびグラフから、固定端の位置を固定したまま梁を曲げることで最大3倍近くまで共振周波数が上がっていることがわかります。
共振周波数が上がる大きな要因として、梁を曲げることにより共振時に直線梁で大きく変形していた中心部分での並進変位を抑えたことがあります。
解析解の導出で仮定したように、梁が長手方向に固くほぼ伸び縮みしないことから、梁の曲げ部では幾何的に並進変位がほとんどできなくなると考えられます。
曲げ角度がある程度大きい状況で解析解とシミュレーション結果が一致することからこの仮定が正しいことが推察され、今回の解析条件では曲げ角度が0~10°の間で中心部が大きく変位するモードから変位しないモードへ移り変わっていると考えられます。
曲げた部分で並進変位が抑えられていることは、共振周波数における変位を可視化することでもわかります。
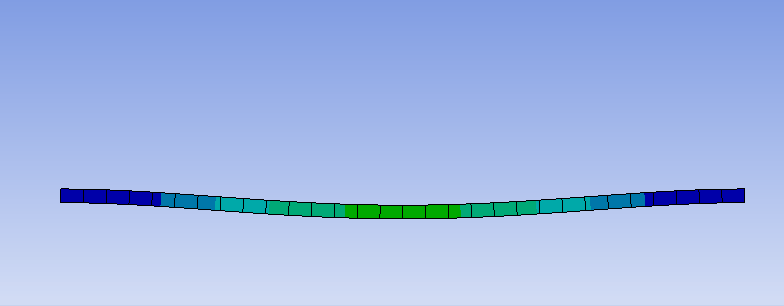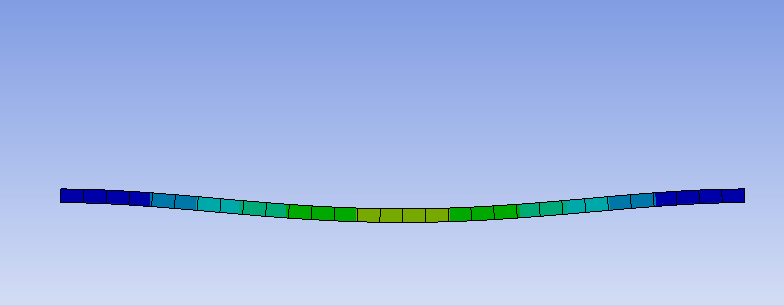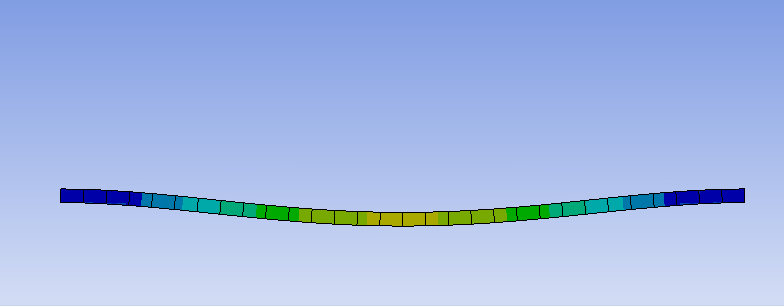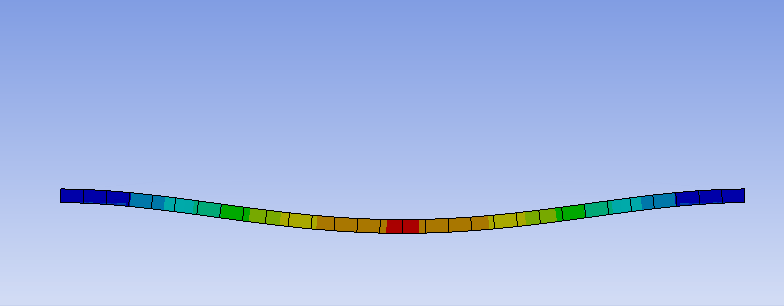
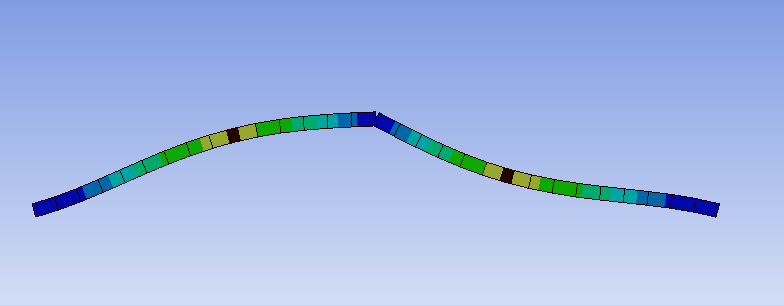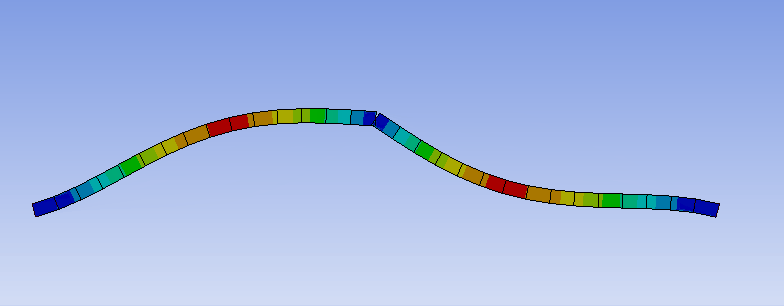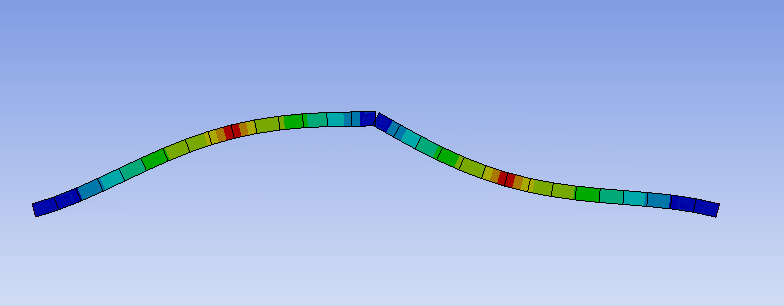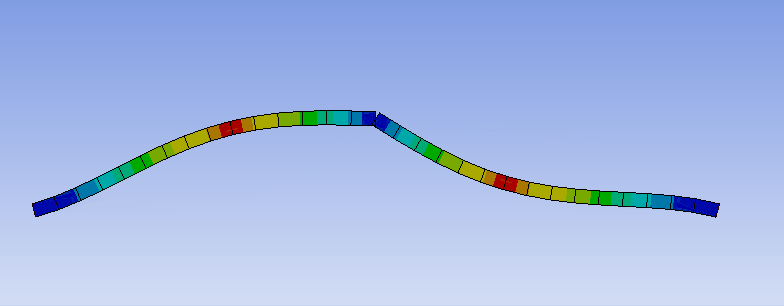
このように、単純に構造を曲げるだけでも共振周波数を高くすることができ、防振構造の形状の工夫で防振可能な周波数帯を広げられる可能性を示しています。
まとめ
本記事では、防振において問題となる構造のサージング(固有振動)についてや、梁構造でのサージングの評価と形状の工夫により共振周波数を大きく変えられることを紹介しました。
次の記事では、どのような考えのもとサージングを考慮した防振構造設計を行っているか紹介していきます。

