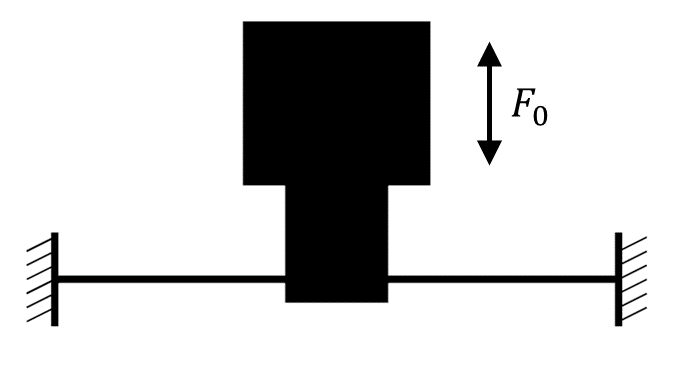(1)サージングを考慮した防振構造の設計の続きの記事です。

防振構造の防振可能な周波数帯の評価

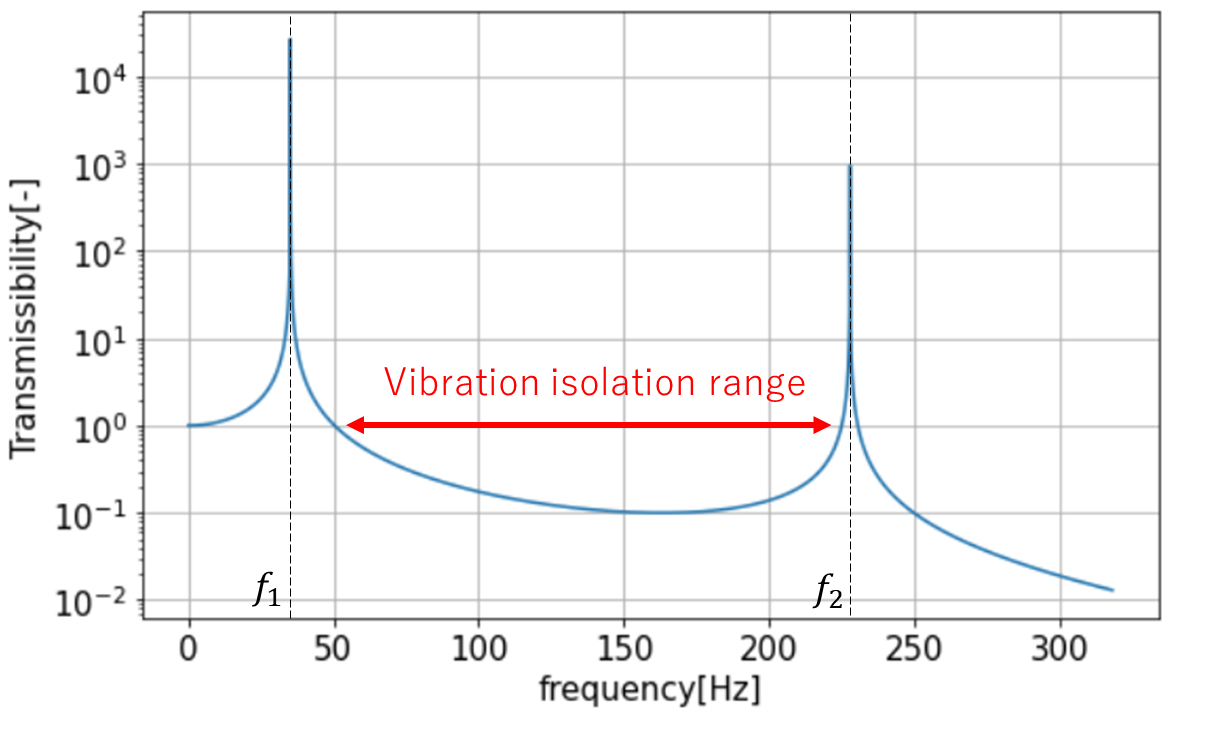
防振構造のサージングにより、防振可能な周波数帯が限られたものになります。 周波数帯の下限を決める1次共振周波数を小さくし、上限を決める2次元共振周波数を大きくすれば防振可能な周波数帯を広げることができます。

多くの場合、マウント質量m_1は防振構造の質量m_2よりも十分大きくなります。 このような状況において、1次共振周波数f_1はマウント質量m_1と防振構造の剛性kから作成した1自由度ばねマスモデルの共振周波数により、2次共振周波数f_2は質量マウント部が固定された状態での防振構造の共振周波数によりおおよそ決まります。 そのため、剛性が小さく共振周波数が大きい防振構造を作れば、防振可能な周波数帯が広くなります。

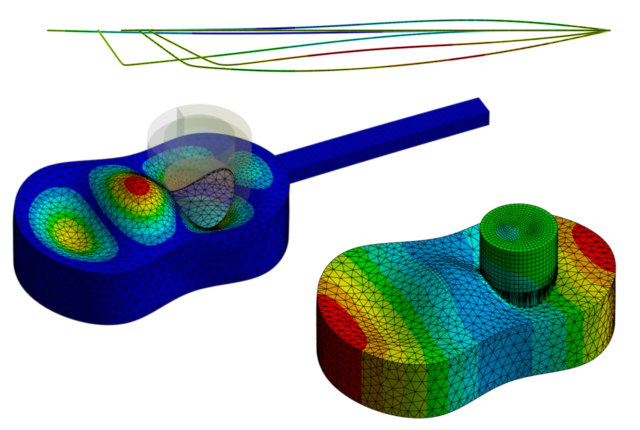
ここで、前記事で共振周波数の評価をした、直線梁および曲がった梁に挟まれた左右対称な防振構造を考えることにします。

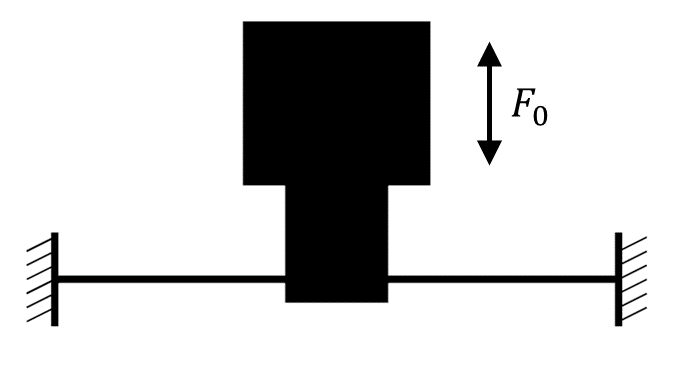
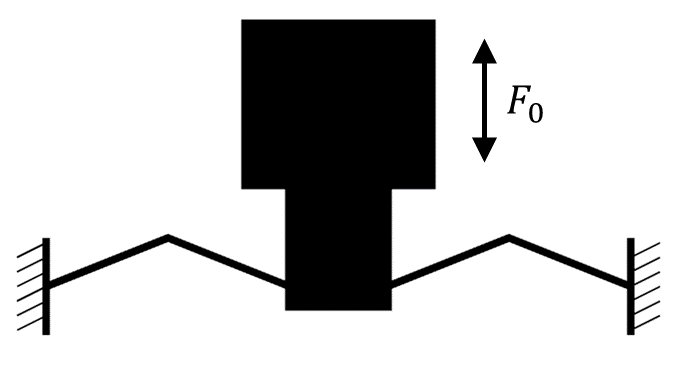
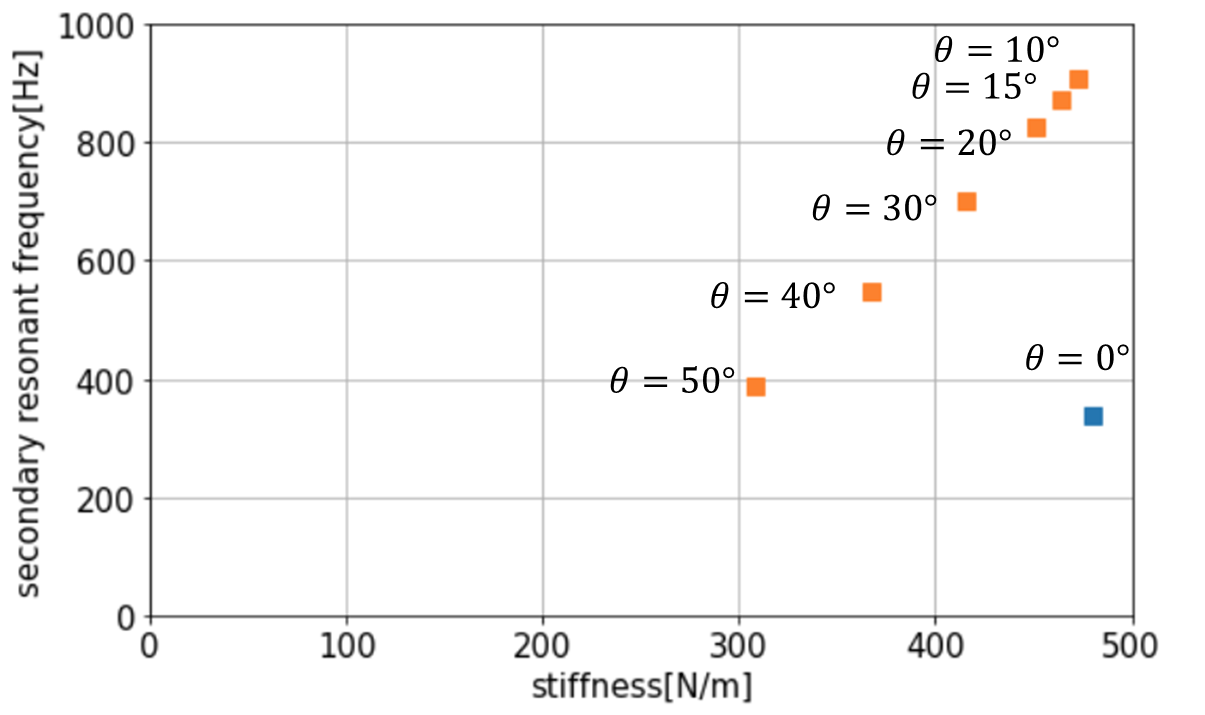
梁部の寸法を以下のようにおき角度\thetaを振ると、以下のように剛性と防振構造の共振周波数（防振系全体の2次共振周波数f_2）がマッピングされます。

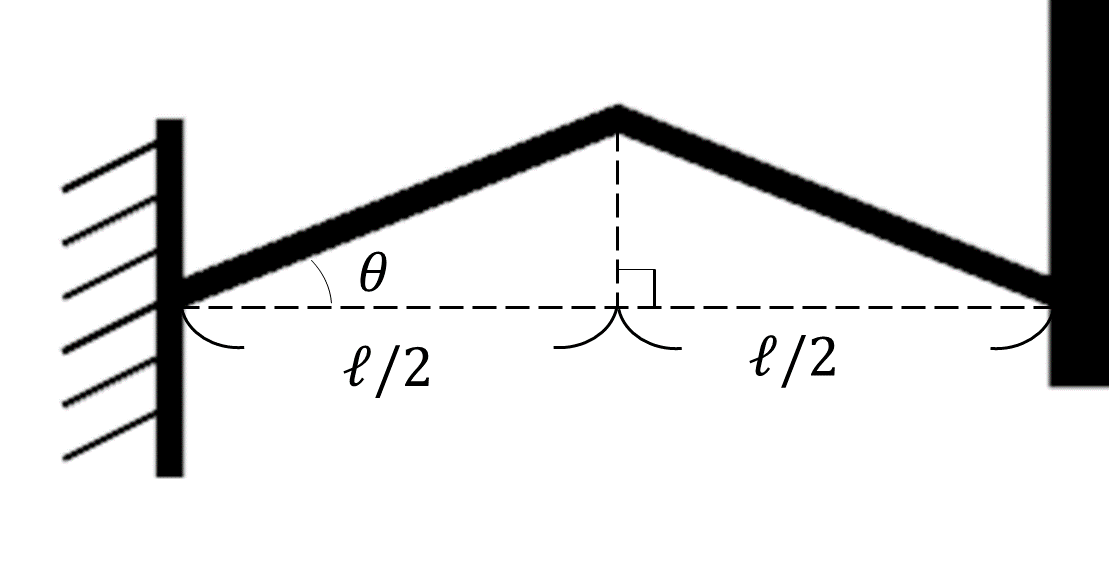
ここで、ヤング率E=3\rm{GPa}、密度\rho=1100\rm{kg/m^3}、長さ\ell=0.1\rm{m}とし、梁断面は長方形断面（奥行き0.01\rm{m}、高さ0.002\rm{m}、断面積A=0.00002\rm{m^2}、断面二次モーメントI\simeq6.67\times10^{-12}\rm{m^4}）としました。 また、共振周波数は前記事で導出した解析解を使用し、剛性kについても梁理論により微小変形を仮定して導出した以下の解析解を使用しました。

    \begin{align}
        k&=
        \left\{
        \begin{array}{lc}
            \displaystyle
            \frac{24EI}{\ell^3} && (\theta=0°)\\
            \displaystyle
            \frac{24EI}{\ell_1^3}(u_1^2+u_2^2)+\frac{12EI}{\ell_1^2}\theta_1(u_1+u_2)
            && (\theta\geq 10°)
        \end{array}
        \right.
        \tag{1-1}
        \\
        \ell_1&= \frac{\ell}{\cos\theta}
        \tag{1-2}
        \\
        u_1&=\frac{\sin \theta}{\sin 2\theta}
        \tag{1-3}
        \\
        u_2&=-\frac{\sin \theta}{\tan 2\theta}+\cos\theta
        \tag{1-4}
        \\
        \theta_0&=\frac{3(u_1+u_2)}{2\ell_1}
        \tag{1-5}
    \end{align}

マッピングしたグラフは横軸を剛性、縦軸を防振系全体の2次共振周波数にとっているため、左上にあるものほど防振周波数帯が広いことになります。 そのためプロットした\theta=10\sim50°の構造は、\theta=0°と比べ防振周波数帯を広げているといえます。

マウント質量をm_1=0.02kgとすると、\theta=0°,10°における周波数応答は以下のようになります。

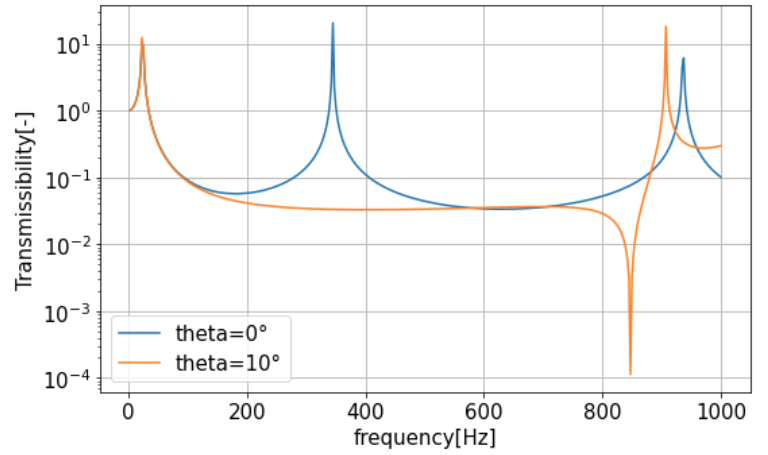
\theta=0°,10°は剛性がほぼ同じであることから1次共振周波数はほぼ変わらず、\theta=10°のほうが2次共振周波数が大きく防振周波数帯が広くなっていることががわかります。

サージングを考慮した防振構造の設計

ここまででは現象を理解するために単純な梁形状において解析解でサージングを評価していました。 実際の防振構造は複雑で、様々な要件と制約（応力要件、製造制約、サイズ制約など）が関わることから、シミュレーションを用いながら設計します。

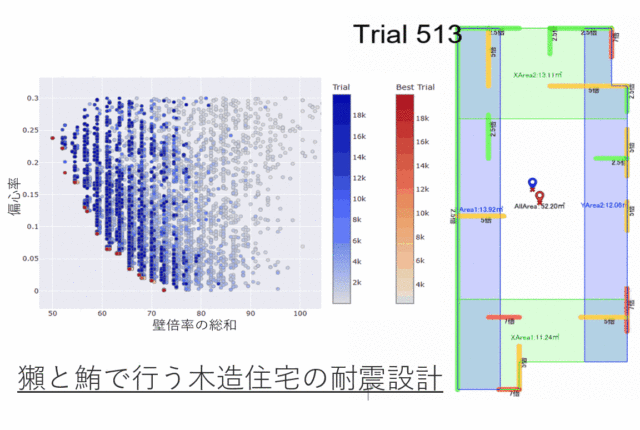
シミュレーションによる解析で、厚さ一定な二次元梁構造の制約のもと下記図の赤枠内の構造を変えて、剛性と2次共振周波数をマッピングした例を示します。

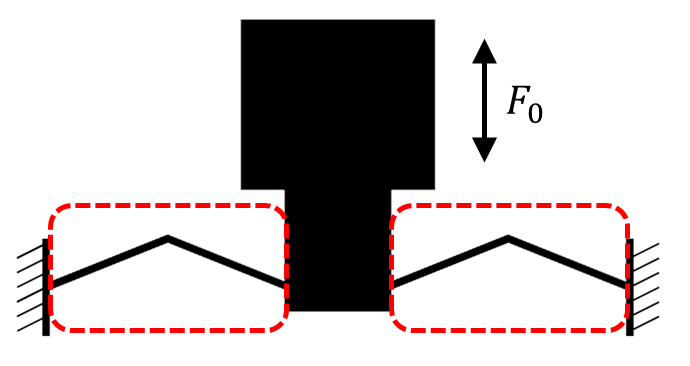
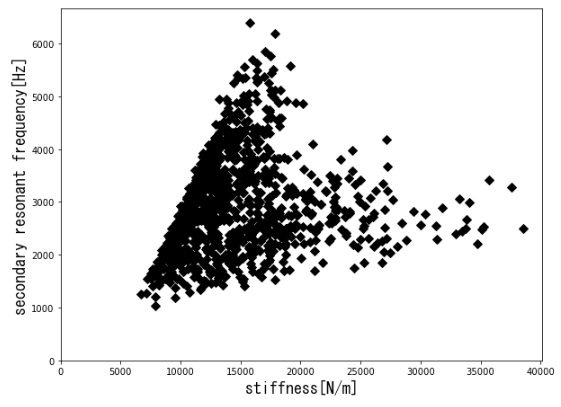
自明な結果ではありますが、剛性と2次共振周波数のマッピングの左上部にパレート面ができています。 パレート面近傍には上で示した梁を曲げた構造だけでなく、円弧上の構造なども現れています。

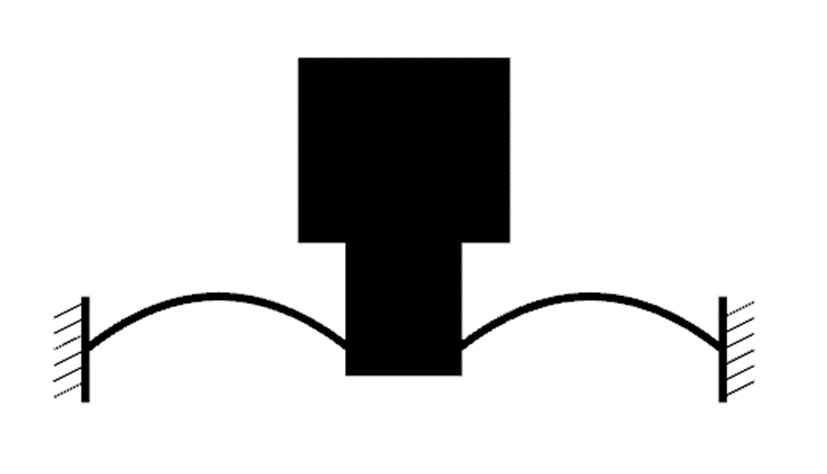
構造の制約を緩めたり材料を変えたりすることで、パレート面を拡張することができます。 実際の設計では要件と制約を定義したうえで、解析する系に合わせて簡易解析（梁要素、サロゲートモデルなど）と詳細な解析を併用しつつ構造を探索しています。

まとめ、著者コメント

前記事と本記事では、防振において問題となる構造のサージング（固有振動）について説明し、サージングを考慮した防振構造の設計に関して紹介しました。 サージングの対策としては形状を変えて防振周波数幅を広げる以外にもいくつも方法があります。 梁厚の分布による剛性-2次共振周波数のパレート面を拡張や、変位増幅機構と減衰機構を組み合わせて共振周波数における振動伝達率を低減させるといったこともなされています。

個人的に数式が好きなので、数式を盛り込んだ記事としました。