はじめに
設計最適化を熱流体問題に適用することにより、人間では設計が難しい複雑形状で非常に高性能な流路形状を生成することが可能です。しかし、特にトポロジー最適化では、量産が難しい複雑形状が生成されることが多く、実務に適用する際の課題となります。また、熱流体問題をCFDで直接解くのは計算コストが大きく、最適化に取り込むと計算時間が膨大になってしまうという別の課題もあります。
今回の記事では、Darcy–Forchheimer則を取り入れた均質化法により最適な冷却流路を設計した研究[1-3]をとりあげます。この研究では、大きな周期的ユニット構造を多孔体として近似(均質化)し、トポロジー最適化のアルゴリズムを用いて冷却流路を創出し、その手法の有効性を数値解析と実験の両面から検証しています。
この研究では金属3Dプリンターのような積層造形による流路製造を念頭に置いていますが、円柱列のような簡単な準2D形状からなる流路であれば、鋳造など量産性の高い製造法にも展開できるのではないかと私たちは注目しています。
均質化法は通常、微細な周期構造が大量に繰り返される場合に使われます。しかし本研究では、比較的大きなユニット構造を用いた場合でも十分な精度が得られることを実証しています。
本記事では、[2]の論文の内容を紹介しながら、その結果の再現を試みます。
論文紹介
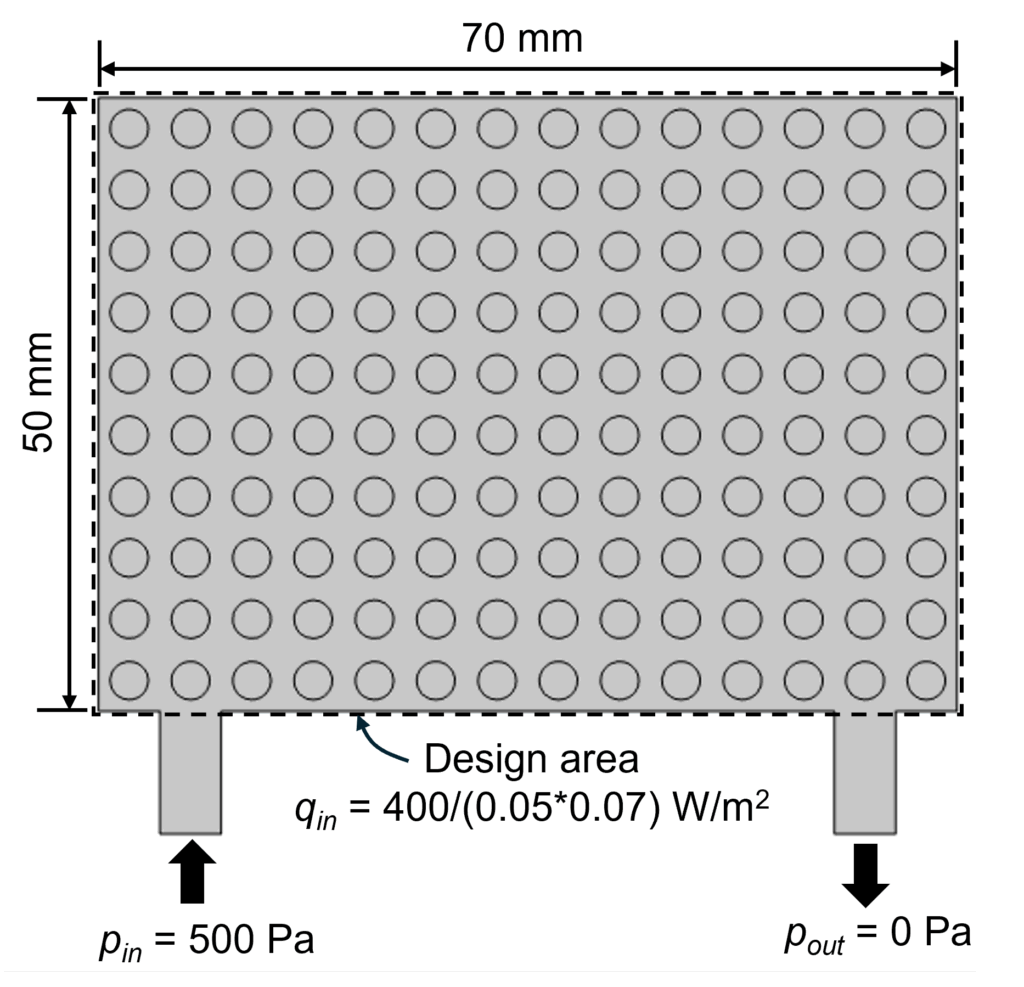
この論文[2]では、図1のように70 mm x 50 mmの設計領域(流路厚み5 mm)に140個の円柱が周期的に置かれている場を考え、その1つ1つの円柱の寸法に分布をつけることで流路形状を創出します。円柱の直径はD=1.0+3.0dで定義され、設計変数d\:(0\le d\le1)の最適化を行います。
ユニットセル構造を多孔体として扱う
この構造でそのまま流体シミュレーションおよび最適化を行うと、膨大な計算コストがかかります。そこでユニットセル構造を多孔体として近似(均質化)し、Darcy–Forchheimer則に基づいて流体の運動を記述します。ここでは上の図1において周期的に繰り返される1つの円柱まわりの空間をユニットセルとして切り出します。なお、均質化については以下の過去のテックブログでも扱っておりますので、興味のある方はご参照ください。
このDarcy–Forchheimer則では、ユニットセル内部を流れる流体に働く圧力損失を以下の式で表します:
\nabla p = -\frac{\mu}{\mathbf{\boldsymbol\kappa}}\mathbf u- \rho \boldsymbol\beta|\mathbf u|\mathbf uここで、pは圧力、\muは粘性係数、\boldsymbol\kappaは透過率、\bold uはDarcy速度、\rhoは密度、\boldsymbol\betaはForchheimer係数を意味します。
ユニットセル内部の形状を変えると\boldsymbol\kappaや\boldsymbol\betaが変化し、それが流れ場に影響を与えます。その形状の変化に対して透過率やForchheimer係数がどう変化するのかを調べるために、ユニットセル内の流体解析を行ってその特性を調べます。この手順は、上記の過去の弊社の均質化に関するテックブログでも行われております。
ここでは図2のようにユニットセル内部の物体の寸法および境界条件の圧力値を変化させながら流体解析を実施し、圧力勾配と流速の関係から\boldsymbol\kappaと\boldsymbol\betaを同定します。同様に、ユニットセル内部の熱伝導解析から有効熱伝導率\boldsymbol\lambda^*を算出します。
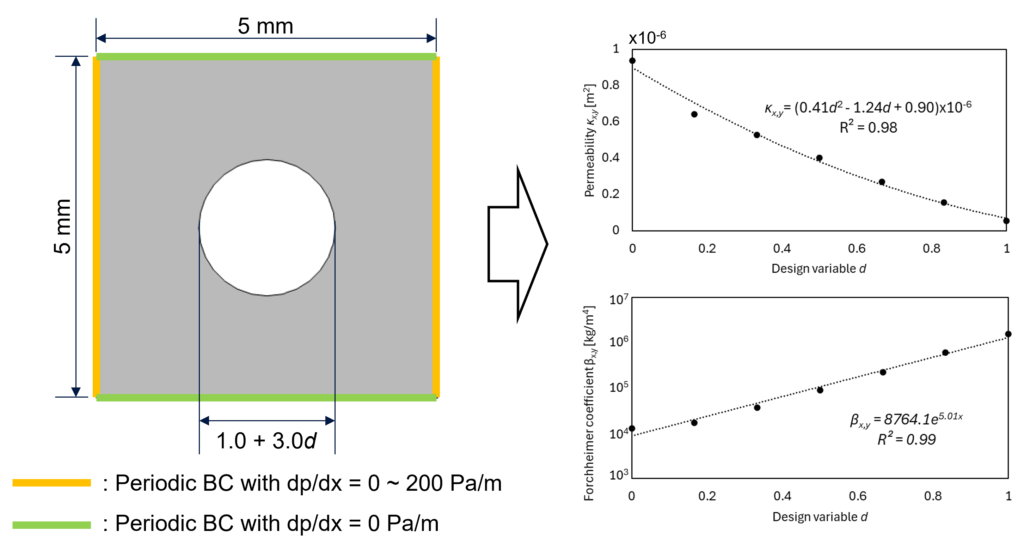
\boldsymbol\kappaと\boldsymbol\beta
最適化の問題設定
以上のユニットセル計算で得られた物性を用いて、実際に円柱列の直径分布を最適化していきます。実際の製品では、同じだけの仕事を行った時にできるだけ流量が多かったり、より物体を冷やせている方が嬉しいことがあります。すなわち、最適化の問題設定としては、目的関数は流入部流量および設計領域の平均表面温度とし、それぞれの最大化および最小化を行います。制約条件として、固体部が占める割合が30%以上となるよう体積制約を設定します。
計算条件
支配方程式には多孔体内の流体の運動を記述する方程式であるBrinkman–Forchheimer方程式と熱伝導・対流方程式を用いて有限要素法で離散化します。感度解析は随伴法で計算、設計変数の更新はMMA(Method of Moving Asymptotes)を用います。
境界条件は、図1に示すように入口と出口にそれぞれ500 Paと0 Paの圧力指定、流入温度は25℃とし、設計領域底面に一様に400/(0.05*0.07) W/m^2の熱流束を与えます。流体部には水、固体部にはステンレスの物性を用います。設計変数の初期状態は全体に一様にd = 0.7に設定します。
最適化結果
はじめに、図3に初期状態の速さおよび温度分布を示します。ある程度全体に流れが行き渡ってはいるものの、外周には十分に流れが行き届かないため、外周沿いの特に右上の角付近が広く高温になっています。
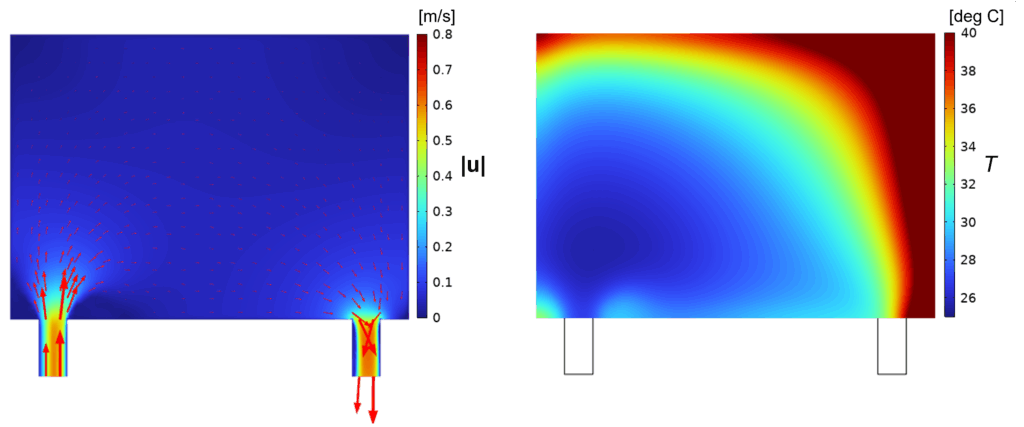
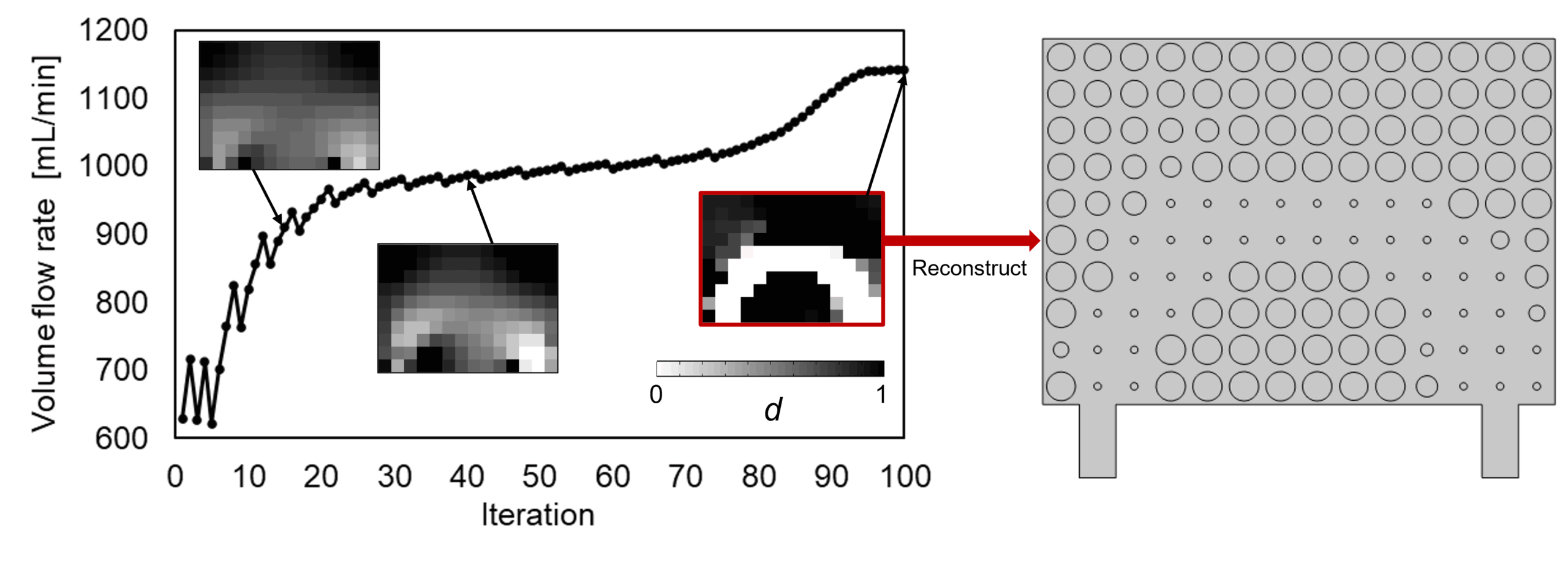
次に、流入部の流量を目的関数としてそれを最大化する設定での最適化結果を示します。図4は目的関数の履歴と設計変数分布の変化の過程および100step目の設計変数分布から再構築した円柱列です。この図から、初期状態から流量が増加していくこと、また徐々に明確な流路が現れていることがわかります。100step目の結果から再構築した円柱列を見ると、入口から出口を滑らかに繋ぐU字の領域で細い円柱ができ、それ以外の領域で太い円柱が形成されていることがわかります。
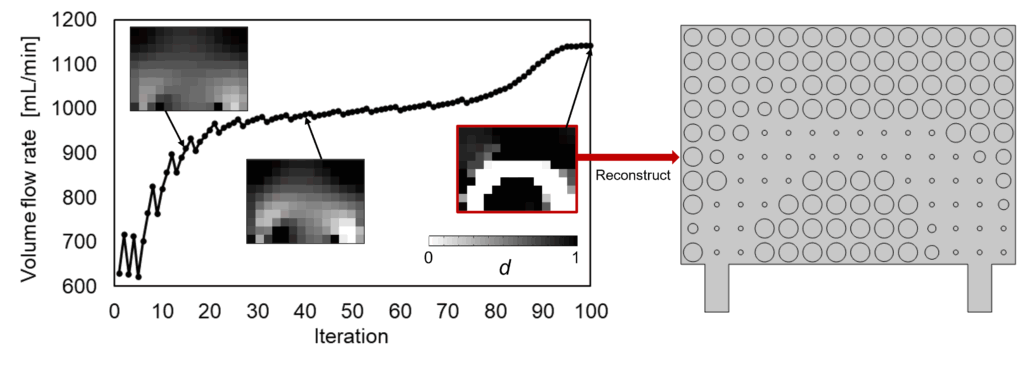
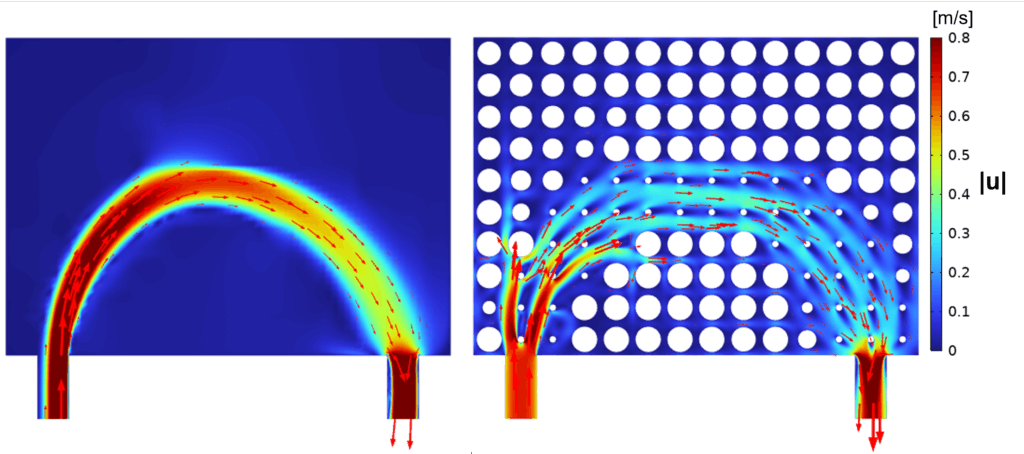
図5に100step目における速さの分布と、100step目の設計変数分布から再構築した円柱列を対象に細かいメッシュでCFD計算(以下、高忠実度CFDと表記)を行った結果を示します。左の最適化の計算結果を見ると、設計変数が小さかった領域に乗る形で高速な流れが形成されており、入口と出口が少ない抵抗の流路で結ばれたことで流量が増えたことが確認できます。右の高忠実度CFDの速さ分布を見ると、速度の絶対値は最適化の計算結果とは異なっているものの、物理量の分布は同様であることが確認できます。
次に、設計領域の平均温度を目的関数としてそれを最小化する設定で最適化を行います。図6が目的関数の履歴と設計変数分布の変化の過程および100step目の設計変数分布から再構築した円柱列です。流量最大化の時と同様、平均温度は段々低下し、明確な流路が現れていく過程が見て取れます。最終的に生成された円柱列を見ると、外周に沿って円柱がやや細い領域が形成されていることがわかります。
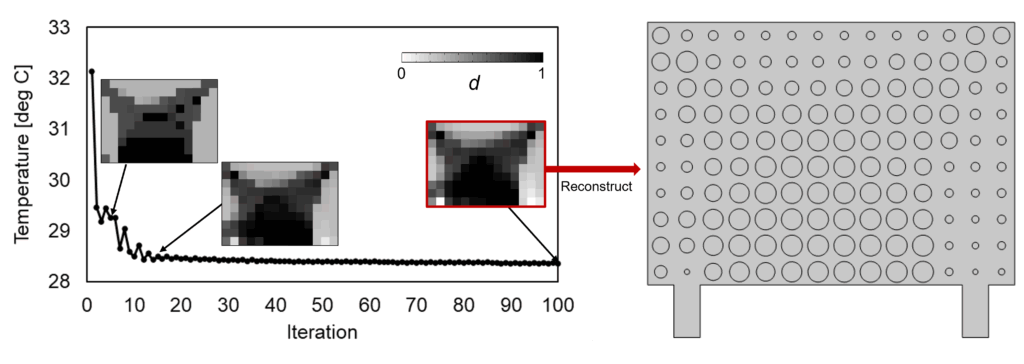
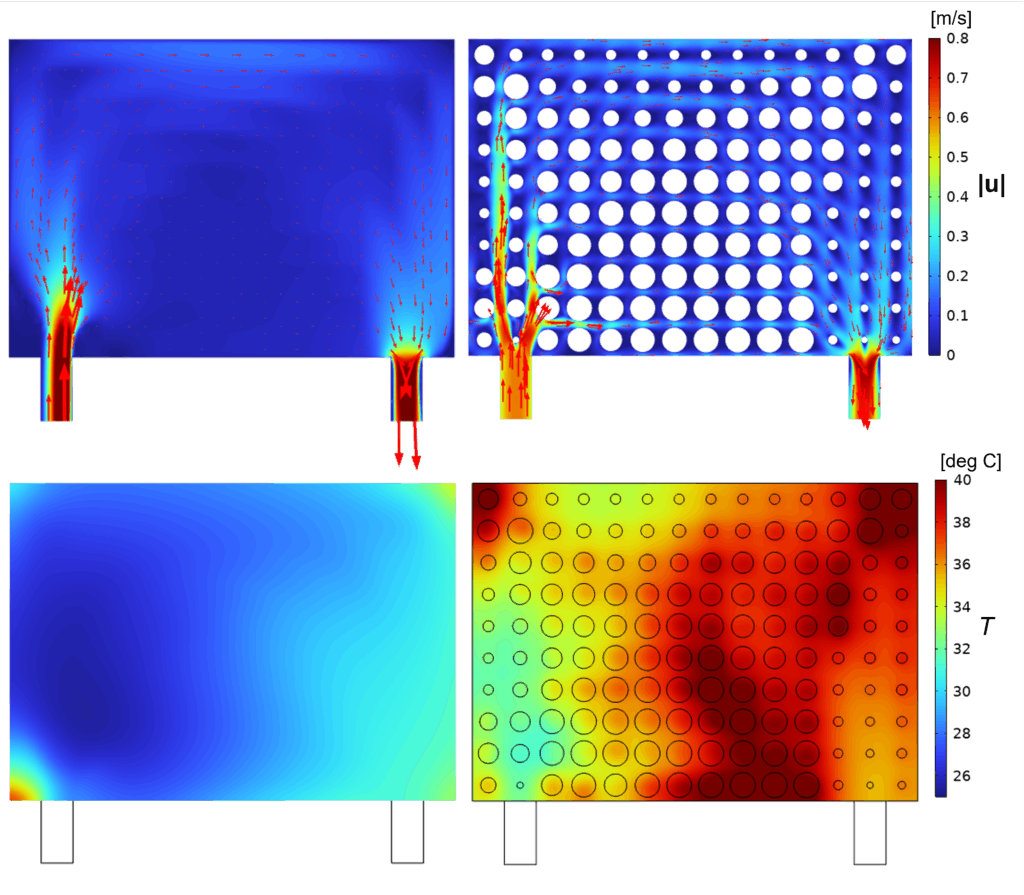
図7に最適化100step目および高忠実度CFDの速さと温度分布を示します。左側に示す最適化の計算結果を見ると、図3の初期状態において高温であった外周に沿って流速が大きくなっていることが確認でき、外周に十分に水が届くような設計変数分布となることで、高温部が抑制されていることがわかります。右側に示す高忠実度CFDの速さ分布を見ると、入口付近から出口付近に直接向かう流れが最適化の計算結果よりも強く表れているものの、入口から外周付近を回って出口に向かう流れが生じていることが確認できます。一方で、温度分布を見ると、最適化の計算結果よりも明らかに全体的に温度が大きくなっています。しかし、外周にそって高温部が抑制されているという点では、最適化の計算結果と同様の傾向であると言えます。
以上の結果は、論文に示されていたものと細かな違いはあれど、おおむね整合する結果でした。全体的に、物理量の分布の絶対値は最適化の計算結果と高忠実度CFDの結果で一致はしないものの、分布の傾向自体は大きく外れることはないという結果でした。実際の機械設計においては、もちろん両者は一致しているに越したことはないものの、その一致が必ずしも必要かというと、そうではありません。設計で重要なのは、形状を変更したときに物理場がどう変化するかの傾向を把握することです。この最適化の計算は、高忠実度CFDと比べて近似度合いが強いものの、設計の方向性を与える役割としては十分に機能すると考えられます。
この手法は最適化の前段階としてユニットセル計算を行う必要があるものの、最適化自体の計算コストは高くなく、以上の140個のパラメータの最適化を手元のデスクトップPC(一般的なゲーミングPC程度のスペック)で40分程度で行うことができました。
おわりに
今回の記事では、大きな周期的構造を多孔体と近似することで低コストで最適な冷却流路構造を創出する手法に関する論文の紹介と、その結果の再現を行いました。
この手法を用いることで、単純な形状が規則的に大量に並ぶ系において、低計算コストで効率的な冷却流路構造の設計最適化が可能です。論文[1]では3Dプリントを前提とした3次元形状のユニットセル構造を用いておりますが、円柱列のような比較的シンプルな形状を用いれば、製造面での実現性も高い冷却流路設計が可能と言えます。
しかしながら、この研究は十分に低いレイノルズ数の流れを前提としており、産業応用の観点ではそのままでは限界があります。
当社では、こうした最先端の学術的知見を踏まえつつ、産業的に重要となる高レイノルズ数域の流れに対応できるような最適化手法の研究を進めています。実際の製品開発に直結する規模・条件での最適設計を実現することで、私たちはこの技術のような先進的な最適化手法の実用化を加速させ、より高性能な冷却系設計ソリューションを社会に届けることを目指しています。
参考論文
[1] Takezawa, A., Zhang, X., Kato, M., and Kitamura, M., “Method to optimize an additively-manufactured functionally-graded lattice structure for effective liquid cooling,” Additive Manufacturing, Vol. 28, 2019, pp. 285-298. https://doi.org/10.1016/j.addma.2019.04.004
[2] Takezawa, A., Matsui, K., Murakoshi, S., Taniguchi, K., Moritoyo, R., and Kitamura, M., “Validity of the quasi-2D optimal variable density lattice for effective liquid cooling based on Darcy–Forchheimer theory,” Thermal Science and Engineering Progress, Vol. 55, 2024, pp. 102898. https://doi.org/10.1016/j.tsep.2024.102898
[3] Yanagihara, K., Murakoshi, S., and Takezawa, A., “Fin angles optimization of water-cooled plate-fin heat sink based on anisotropic Darcy–Forchheimer theory,” International Journal of Heat and Mass Transfer, Vol. 236, 2025, pp. 126325. https://doi.org/10.1016/j.ijheatmasstransfer.2024.126325