0. はじめに

弊社では、ある機能条件が与えられた際に、さまざまな最適化手法を駆使して構造形状を設計しています。それぞれの手法には長所と短所があり、問題設定やパラメータの調整、手法の組み合わせなど、多くの工夫と試行錯誤が必要とされます。

一方で、近年、深層学習(DL; Deep Learning)を用いた生成技術の発展はめざましく、入力指示に従って文章や画像を自動生成することが当たり前になりつつあります。

もし、DLを用いて、条件から直接構造形状を導出できる生成モデルが実現できれば、こうした試行錯誤を省略でき、設計業務が非常に効率化されることでしょう。はたして、設計の分野においても、条件を入力するだけで適切な形状が得られるような生成モデルは実現可能なのでしょうか。

1. 生成モデルについて

生成モデルは、学習データに基づき「もっともらしい」新たなデータをに生成します。
深層ニューラルネットワークを用いた生成モデルも多数種類がありますが、今回は筆者の理解と実装が最も早かった敵対的生成ネットワーク(GAN; Generative Adversarial Network)を採用しました。
GANは生成器(Generator)と識別子(Discriminator)という2つのニューラルネットワークを互いに競わせながら学習を行うことで、学習データに類似した画像を生成することができるようになります。明瞭な境界が得られやすく、高速に生成できる点が主な利点です。

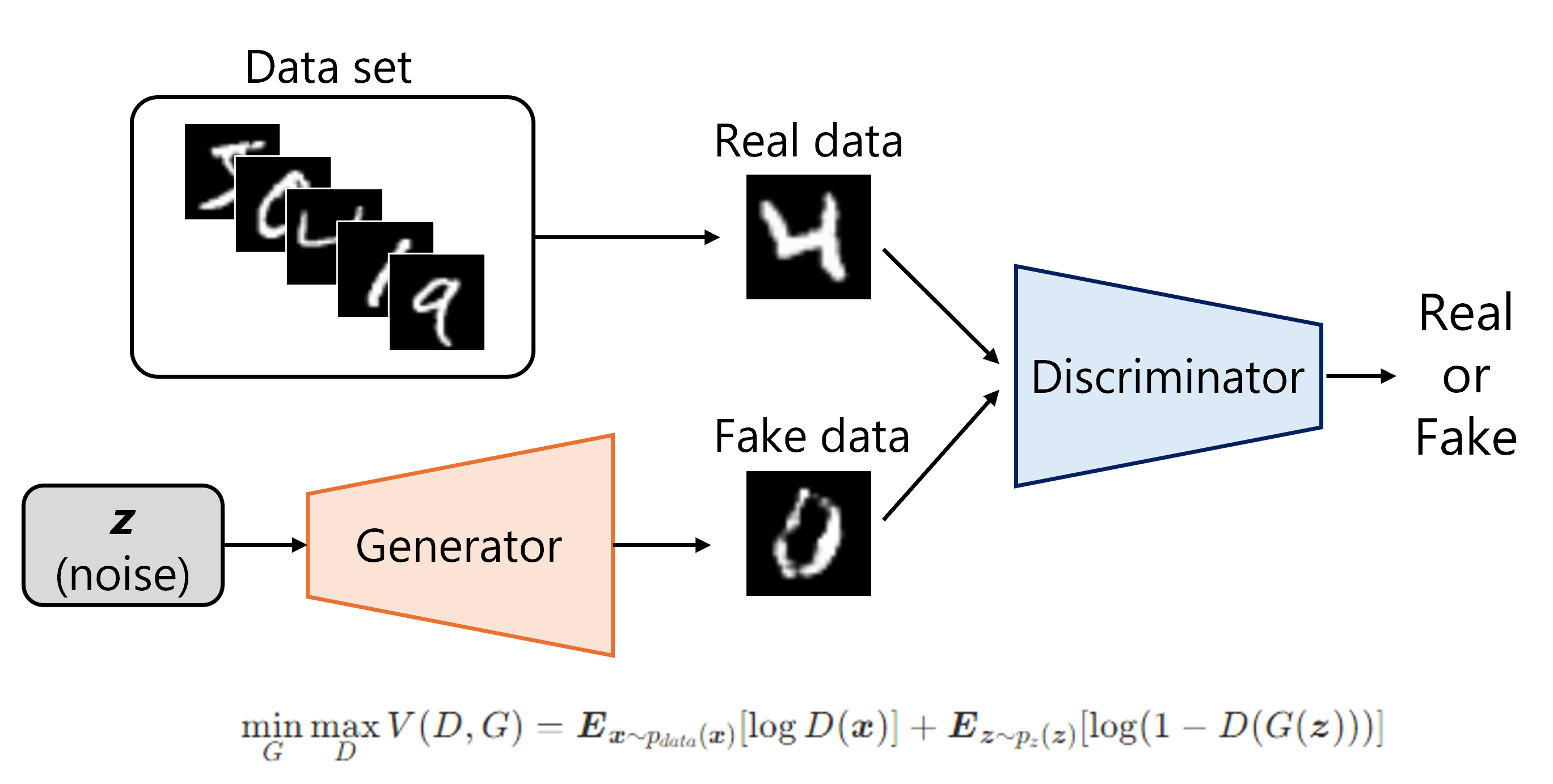
標準的なGANでは、出力される画像はランダムノイズに依存するため、生成結果を制御することができません。

そこで、条件付きGAN（Conditional GAN, cGAN）を用います。生成器と識別器の入力に条件ラベルも含めることで、条件に応じた出力を可能とする手法です。これにより、特定の機能条件を満たす構造形状を生成する、といった目的に対しても応用できそうです。

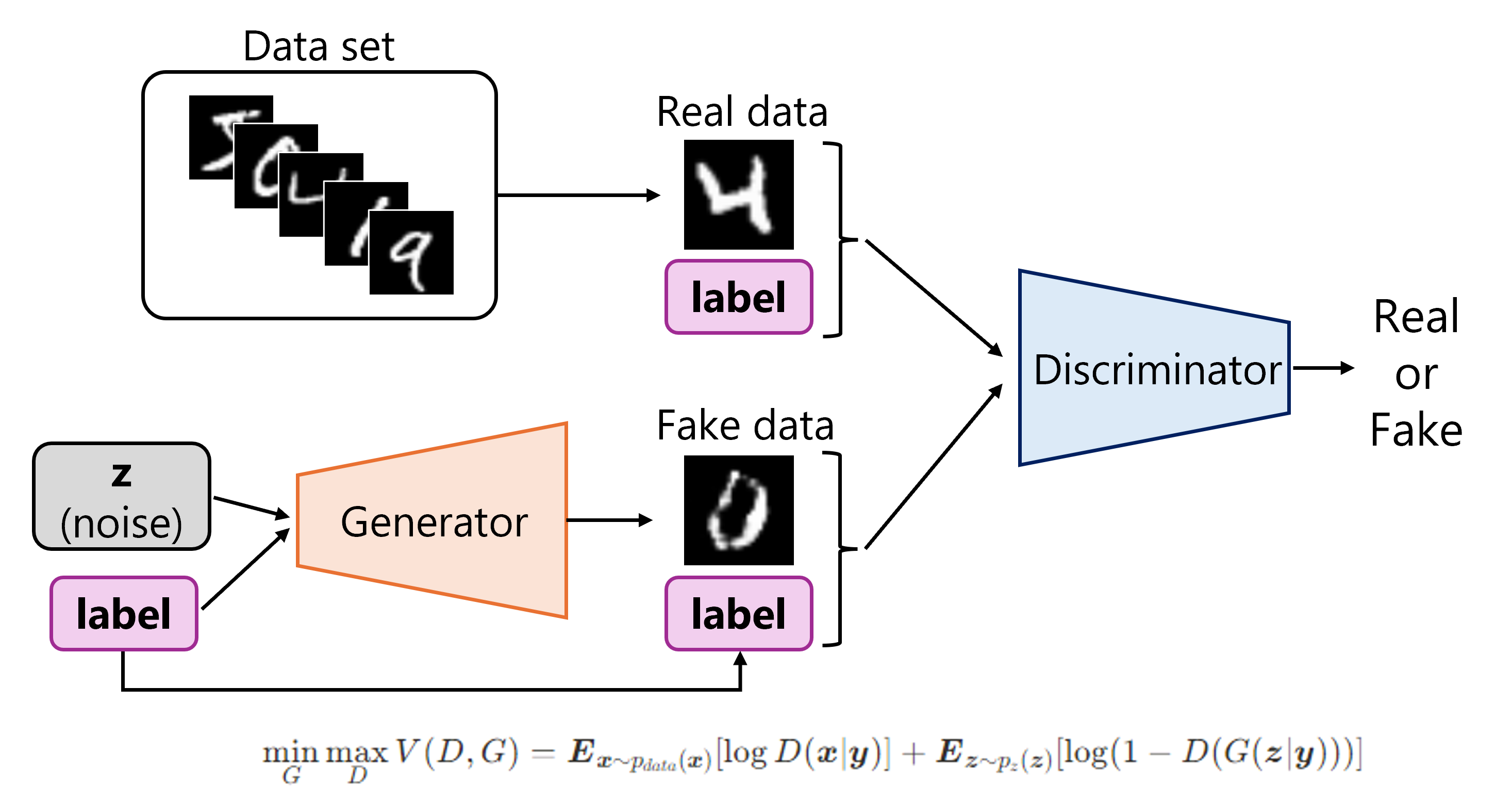
本稿では生成モデルの詳細な説明については割愛します。より正確かつ包括的な解説をご希望の場合は、専門書や学術文献をご参照ください。

2. 設計対象

機能から形状を生成する対象として、チェッカープレートのように周期的な凹凸を有する板材を取り上げます。

チェッカープレートの凹凸形状は滑り止めを目的していると考えられますが、このような凹凸形状は板の曲げ剛性の向上にも有効です。

このような周期的な凹凸を有する板材のマクロな曲げ特性は、連続体のシェル要素として均質化できます（以前の記事）。今回は簡単のため、直交異方性材を仮定します。また、ねじり剛性に関する成分は無視して曲げ剛性成分のみに着目します。

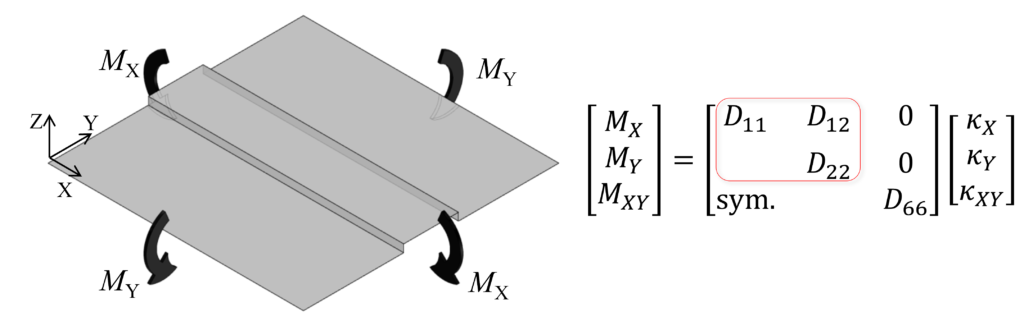
例えば、図のように凹凸がX方向に長く伸びている場合、X方向に関する曲げ剛性は高く、Y方向に関しては柔らかくなります。すなわち、曲げ剛性行列において、D_{11}成分が大きく、D_{22}成分が小さくなります。

実際の設計においては、状況に応じて「ちょうどよい特性」を有する部材が求められる場面がしばしばあります。今回は問題設定を単純化していますが、3つの曲げ特性を同時に調整することは、ある程度の専門的訓練を受けた技術者でないと容易ではないでしょう。

3. データセットの作成

生成モデルは、何もないところから作成できるわけではなく、学習するためのデータセットを準備する必要があります。
今回は、多様な形状パターンを含む学習データを作成するために、文字をもとにした凹凸形状を作成します。また、各形状に対して有限要素解析を実施し、条件ラベルに用いる曲げ剛性を算出します。

3.1　解析モデル

今回は直交異方性構造を仮定するため、文字をもとに作成された形状を１ユニット４分の１モデルとして有限要素解析を実施し、曲げ剛性を取得します。
形状作成にあたり、10×10 mmの領域に文字を配置し、それを28×28ピクセルの画像として二値化しました。画像中の文字が存在する領域をビード（凸部）とみなし、解析モデル上ではその部分を盛り上がった構造として扱います。このような角ばったビード形状は製造が困難ですが、今回の検討では解析モデル単純化のため、滑らかな曲線や高さの変化は考慮していません。

ビード高さは一律0.3 mmとし、Z方向重心を通る面を中立面と仮定します。材料条件としてはの板厚0.1 mm、ヤング率1 GPa、ポアソン比0.3を設定しました。
モデル化にはシェル要素を用い、X方向とY方向にそれぞれ曲げ変形させた際の反モーメントから曲げ剛性行列を算出します。

3.2　形状パターン

恣意的な形状選定を避け、データセットに多様性を持たせるため、ひらがなをもとにして形状を作成しました。（ひらがなの起源や形状的特徴に関しては以前の記事をご参照ください。）
使用した文字は、現代仮名遣いに用いられるひらがな46文字に加え、歴史的仮名遣いで用いられる「ゐ」および「ゑ」を含む計48文字です。フォントは游ゴシック体を採用し、スタイル（太字、斜体）や位置、スケールにバリエーションを加えることで計2304個の形状パターンを作成しました。

作成された各形状は28×28ピクセルの画像として保存し、生成モデルの学習に使用します。画像上では盛り上げる部分（ビード）を黒色で表現しています。

3.3　データセットの解析結果

各形状ごとの有限要素解析に要する時間は数秒程度であり、すべてのデータに対する曲げ剛性の算出は数時間で完了します。得られた曲げ剛性成分の結果を下図に示します。

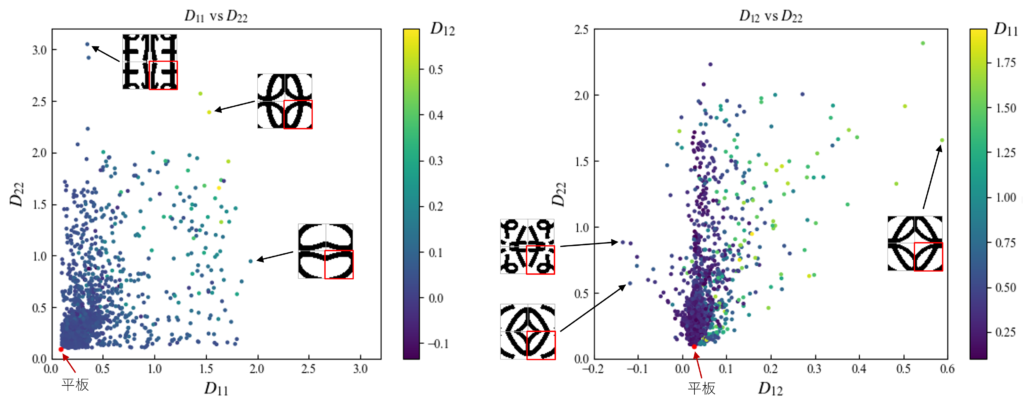
参考として、次式より計算される平板（凹凸なし）の曲げ剛性を赤点でプロットしています。

上下方向に連続する形状が多いため、全体的にy方向曲げ剛性が高い分布となっています。この内容を詳しく観察するだけでも興味深いデータとなっていますが、詳細を語るには余白が足りない本題から外れるため、今回は省略します。

3.4　データ拡張

生成モデルの学習では、学習データの量や分布の偏りがモデル性能に大きく影響します。今回のデータセットでは、文字に由来する縦方向に連続した形状が多いため、Y方向の曲げ剛性が高いサンプルが相対的に多く含まれていました。こうした偏りを緩和し、データの多様性を高めるために、データ拡張（Data Augmentation）を導入しました。

データ拡張(Data Augmentation)とは、既存のデータに対して回転や反転、スケーリングなどの処理を加えることで、データセットのバリエーションを人工的に増やす手法です。

本検討では、回転操作によるデータ拡張を実施しました。
各形状に対して 180°回転を行ったものは、元の形状と同一の曲げ剛性成分を持つため、ラベルの変更なくそのまま使用可能です。一方、90°および270°回転の場合、形状の主方向が入れ替わるため、曲げ剛性行列において D₁₁成分とD₂₂成分を入れ替えることで整合の取れたラベルを付与します。

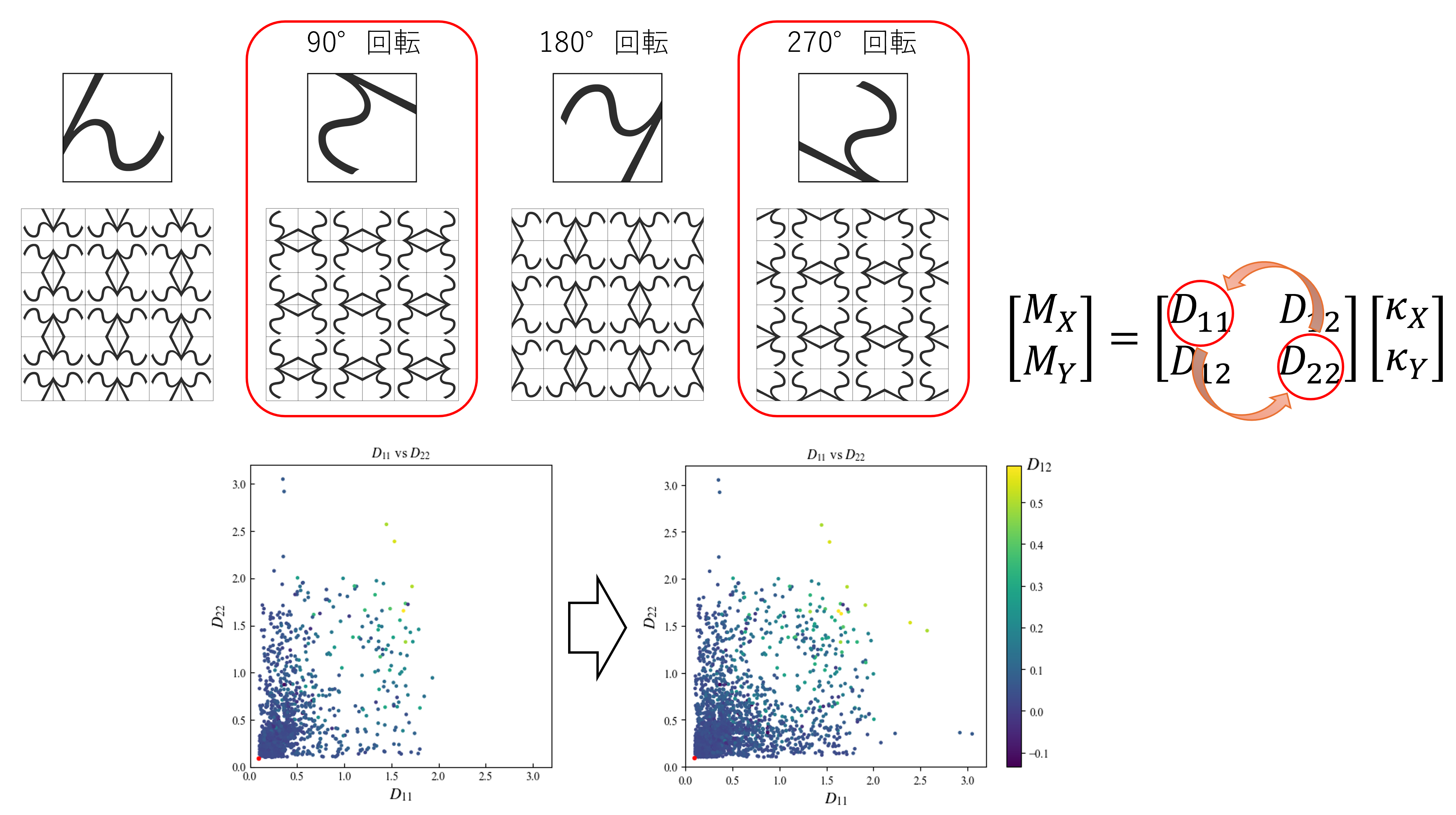
なお、白黒反転（凹凸の反転）や左右反転も同一の曲げ剛性を使用できるため、同様の拡張が可能です。

ただし、今回は出力の多様性よりも学習速度と収束性を優先し、回転操作のみを用いた拡張に限定しました。拡張により、剛性分布の偏りが改善され、データセット全体の件数は4倍に増加しています。

4. NNの構成と学習

生成モデルとして用いた条件付きGAN(cGAN)の構成と学習方法について説明します。

一般的なGANは非常に強力な生成能力を持つ手法ですが、モデルを構成しただけで、期待通りの出力が得られるとは限らず、学習そのものにも多くの課題が伴います。そのため、適切なモデル設計と綿密な試行錯誤が不可欠です。

さらに、今回の目的は指定された条件に合致する形状を生成することにあります。そのため、生成される形状が条件に忠実であること（条件忠実性）が求められます。一方で、今回の問題は1つの条件に対して複数の解が存在し得る（多義的である）という性質もあり、出力の多様性も重要な要素となります。一般に条件忠実性と多様性という相反する傾向にあるため、これらの両立にはモデル構成や学習方法に工夫が必要です。

4.1　GANにおける課題

GANには、次のような課題が存在します：

• 明示的な損失関数が存在せず、性能評価や収束判定が難しい
• 学習が不安定になりやすく、モード崩壊（Generatorが多様なサンプルを出力できなくなる）や学習不均衡（GeneratorとDiscriminatorの性能バランスが崩れ学習が停滞する）が生じる

そのため、以下のような調整が必要となります：

• GeneratorとDiscriminatorのバランスを取るように学習率を調整
• バッチサイズ、潜在空間のサイズ、ドロップアウト、活性化関数などのハイパーパラメータを調整

4.2　学習構成と工夫

今回は、単純な生成器(Generator)と識別器(Discriminator)だけでなく、条件忠実性の向上と出力多様性の確保を目的として、いくつかの工夫を加えた構成としました。以下に、実装上の工夫、ネットワークの構成要素、および損失関数について説明します。

4.2.1　実装上の工夫

学習を安定させ、期待される出力が得られるようにするため、以下の工夫を導入しました。

• Generatorでは条件ラベルの意味付けや学習安定化のため、ラベルを中間層で注入
• 条件忠実性を保つためRegressorを導入し、生成画像から曲げ剛性を推定
• 出力多様性を保つため、入力ノイズの変化が出力差に反映されるようMode seeking損失を追加(MSGAN)

4.2.2　構成要素

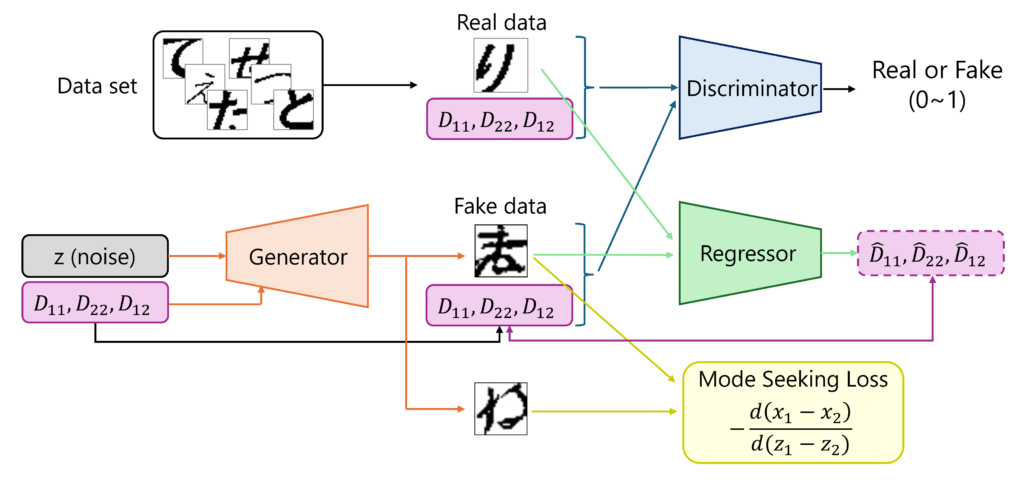
本モデルは、以下の3つのネットワークから構成されます：

• 生成器(Generator)：ランダムノイズ zと条件ラベル（D_{11}, D_{22}, D_{12}）を入力として、画像を生成
• 識別器(Discriminator)：画像と条件ラベルを受け取り、それが実データか偽データかを判定
• Regressor：生成画像から推定される曲げ剛性（\hat{D}_{11}, \hat{D}_{22}, \hat{D}_{12}）を出力し、条件との整合性を確認

4.2.3　損失関数

各ネットワークの損失関数は以下のように定義しました。実画像をx、条件ラベルをy、入力ノイズをzとしています。複数のサンプルをまとめたミニバッチ単位で平均を取って計算してます。

• 識別器(Discriminator)の損失：\text{Loss}_D = -\log D(x,y)-\log(1-D(G(z,y)),y)
  
  識別器（Discriminator）は、実データxが入力された場合は本物であると判断するように、生成データG(z, y)に対しては偽物であると判断するように学習されます。

• 生成器(Generator)の損失：\text{Loss}_G=\underbrace{-\log D(G(z,y),y)}_\text{adversarial}+\underbrace{||R(G(z,y))-y||^2}_\text{regressor}+\underbrace{\text{Loss}_{MS}(G(z,y),G(z',y),z,z')}_\text{mode-seeking}
  
  生成器（Generator）の損失は、識別器を騙すための項 に加え、Regressorを通じた条件忠実性の項、およびMode Seeking損失（\text{loss}_{MS}）を含みます。

• Regressorの損失：LossR=||R(x)-y||^2+||R(G(z,y))-y||^2
  
  Regressorは、実データxおよび生成データG(z, y)のいずれに対しても、正しい曲げ剛性ラベルyを出力できるように学習されます。

　　　

ニューラルネット構成要素および学習に関して、Pytorchを用いて作成したコードの抜粋を以下に示します。必要な処理を一部省略しているため、そのままでは動作しない点をご留意ください。

class Generator(nn.Module):
    def __init__(self):
        super().__init__()

        self.noise_block = nn.Sequential(
            nn.Linear(nz, 64 * 7 * 7),
            nn.BatchNorm1d(64 * 7 * 7),
            nn.LeakyReLU(0.1),
            nn.Unflatten(1, (64, 7, 7)),  # (batch, 64, 7, 7)

            nn.ConvTranspose2d(64, 64, 4, 2, 1, bias=False),  # (batch, 64, 14, 14)
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.1),
        )

        self.label_mapper = nn.Sequential(
            nn.Linear(label_dim, 64),
            nn.BatchNorm1d(64),
            nn.LeakyReLU(0.1),
            nn.Linear(64, 64 * 14 * 14),
            nn.Tanh(),
            nn.Unflatten(1, (64, 14, 14))   # (batch, 64, 14, 14)
        )

        self.net = nn.Sequential(
            nn.ConvTranspose2d(128, 64, 4, 2, 1, bias=False),  # (batch, 64, 28, 28)
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.1),

            nn.ConvTranspose2d(64, 32, 3, 1, 1, bias=False),  # (batch, 32, 28, 28)
            nn.BatchNorm2d(32),
            nn.LeakyReLU(0.1),

            nn.ConvTranspose2d(32, 1, 3, 1, 1, bias=False),  # (batch, 1, 28, 28)
            nn.Tanh()
        )

    def forward(self, z, label):
        x = self.noise_block(z)
        label = self.label_mapper(label)
        x = torch.cat([x, label], dim=1)
        y = self.net(x)
        return y

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(1 + label_dim, 64, 4, 2, 1),  # (batch, 64, 14, 14)
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.1),
            nn.Dropout2d(0.3),

            nn.Conv2d(64, 64, 4, 2, 1),  # (batch, 64, 7, 7)
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.1),
            nn.Dropout2d(0.3),

            nn.Conv2d(64, 128, 4, 1, 0),  # (batch, 128, 4, 4)
            nn.BatchNorm2d(128),
            nn.LeakyReLU(0.1),
            nn.Dropout2d(0.3),

            nn.Conv2d(128, 128, 3, 1, 1),  # (batch, 128, 4, 4)
            nn.BatchNorm2d(128),
            nn.LeakyReLU(0.1),

            nn.Flatten(),   # 2048
            nn.Linear(2048, 1),
            nn.Sigmoid()  # probability (0~1)
        )

    def forward(self, x, label):
        label = label.view(label.size(0), label_dim, 1, 1)  # (batch_size, label_dim, 1, 1)
        label = label.expand(label.size(0), label_dim, x.size(2), x.size(3))  # (batch_size, label_dim, img_size, img_size)

        x = torch.cat([x, label], 1)  # (batch, 1 + label_dim, img_size, img_size)
        y = self.net(x)
        return y

  class Regressor(nn.Module):
    def __init__(self):
        super().__init__()
        self.label_dim = label_dim

        self.net = nn.Sequential(
            nn.Conv2d(1, 32, kernel_size=4, stride=2, padding=1),  # (batch_size, 32, 14, 14)
            nn.BatchNorm2d(32),
            nn.LeakyReLU(0.1),

            nn.Conv2d(32, 64, kernel_size=4, stride=2, padding=1),  # (batch_size, 64, 7, 7)
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.1),

            nn.Flatten(),  # (batch_size, 3136)
            nn.Linear(64 * 7 * 7, 128),
            nn.LeakyReLU(0.1),
            nn.Linear(128, label_dim),
            nn.Tanh()
        )

    def forward(self, x):
        return self.net(x)

# --- Model instantiation ---
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
netD = Discriminator().to(device)
netG = Generator().to(device)
netR = Regressor().to(device)

# --- Loss functions ---
adv_loss_fn = nn.BCELoss()   # adversarial loss
reg_loss_fn = nn.MSELoss()   # regression loss

real_labels = torch.full((batch_size, 1), 0.9, device=device)
fake_labels = torch.zeros(batch_size, 1).to(device)

# --- Single-epoch training function ---
def train():
    netD.train(); netG.train(); netR.train()

    for real_imgs, label in dataloader:
        real_imgs = real_imgs.to(device)
        label = label.to(device)

        # --- Discriminator update ---
        optimD.zero_grad()
        z = torch.randn(batch_size, nz, device=device)
        with torch.no_grad():
            fake_imgs = netG(z, label)

        pred_fake = netD(fake_imgs, label)
        pred_real = netD(real_imgs, label)

        lossD = adv_loss_fn(pred_fake, fake_labels) + adv_loss_fn(pred_real, real_labels)
        lossD.backward()
        optimD.step()

        # --- Generator update ---
        optimG.zero_grad()
        z = torch.randn(batch_size, nz, device=device)
        fake_imgs = netG(z, label)

        # Adversarial loss
        pred_fake = netD(fake_imgs, label)
        loss_adv = adv_loss_fn(pred_fake, real_labels)

        # Regression loss
        loss_reg = reg_loss_fn(netR(fake_imgs), label)

        # Mode Seeking loss
        z2 = torch.randn(batch_size, nz, device=device)
        fake_imgs2 = netG(z2, label)
        loss_ms = mode_seeking_loss(fake_imgs, fake_imgs2, z, z2)

        lossG = loss_adv + lambda1 * loss_reg + lambda2 * loss_ms
        lossG.backward()
        optimG.step()

        # --- Regressor update ---
        optimR.zero_grad()
        lossR = reg_loss_fn(netR(real_imgs), label) + reg_loss_fn(netR(fake_imgs), label)
        lossR.backward()
        optimR.step()

5. 生成形状の評価

指定した条件に対して、どの程度近しい曲げ剛性を持つ形状が生成できているかを評価するため、Generatorから出力された画像をもとに凹凸形状を再構築し、有限要素解析により曲げ剛性を算出しました。

評価は、同一の条件ラベルに対して異なる5つのノイズベクトルを入力し、それぞれから生成された画像を対象に行いました。これを100 epochごとに実施し、学習の進行に伴って生成形状の曲げ剛性がどう変化するかを観察しています。

なお、学習時には各成分の条件ラベル値を次の範囲で正規化し、[-1, 1]にスケーリングしています。

• D_{11} \in [0, 3.2]
• D_{22} \in [0, 3.2]
• D_{12} \in [-0.2, 0.6]

条件ラベルとして(D_{11}, D_{22}, D_{12}) = (0.64, 0.16, 0.04)を指定した場合の生成形状を次に示します。

生成された形状を観察すると、文字の特徴である曲線形状が学習の進行に伴い生成されていることが分かります。また、X方向の曲げ剛性D_{11}がY方向D_{22}よりも大きい条件に対し、どちらかというとX方向に強化される形状が得られており、力学的特徴を適切に反映していることが示唆されます。さらに、入力ノイズを変化させることで異なる複数の候補形状が生成されており、多様性も確保されていることが確認できます。

また、上図の中央の画像について、生成画像を100 epochごとに有限要素解析で曲げ剛性を取得した結果を示します。

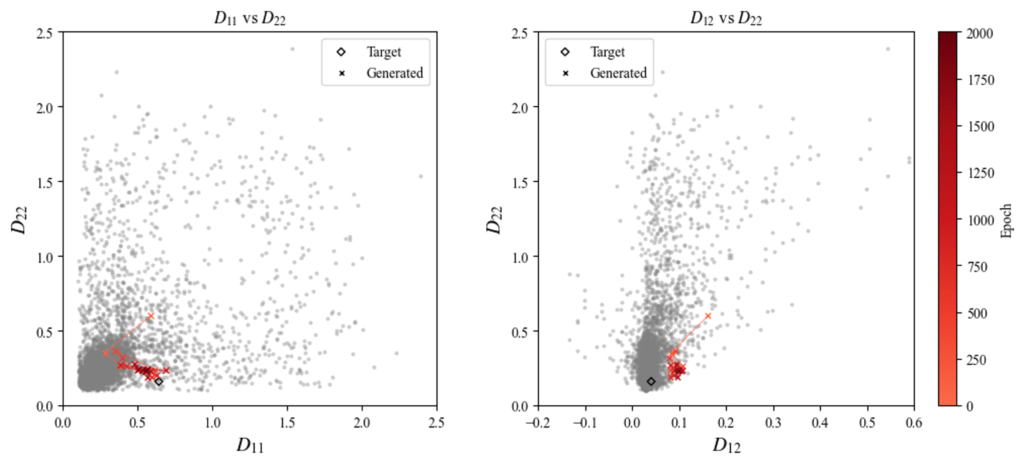
epoch数の増加に伴い、生成形状の曲げ特性が徐々に◇で示す指定条件の値に近づいていく様子が確認できます。

　　　

では、どの条件に対しても指定の曲げ剛性に近い形状を生成できるのでしょうか？
上記を含めた異なる６条件に対して生成した形状を評価しました。各条件に対して異なる5つのノイズベクトルを入力し、2000 epoch後に得られた形状の曲げ剛性を示します。

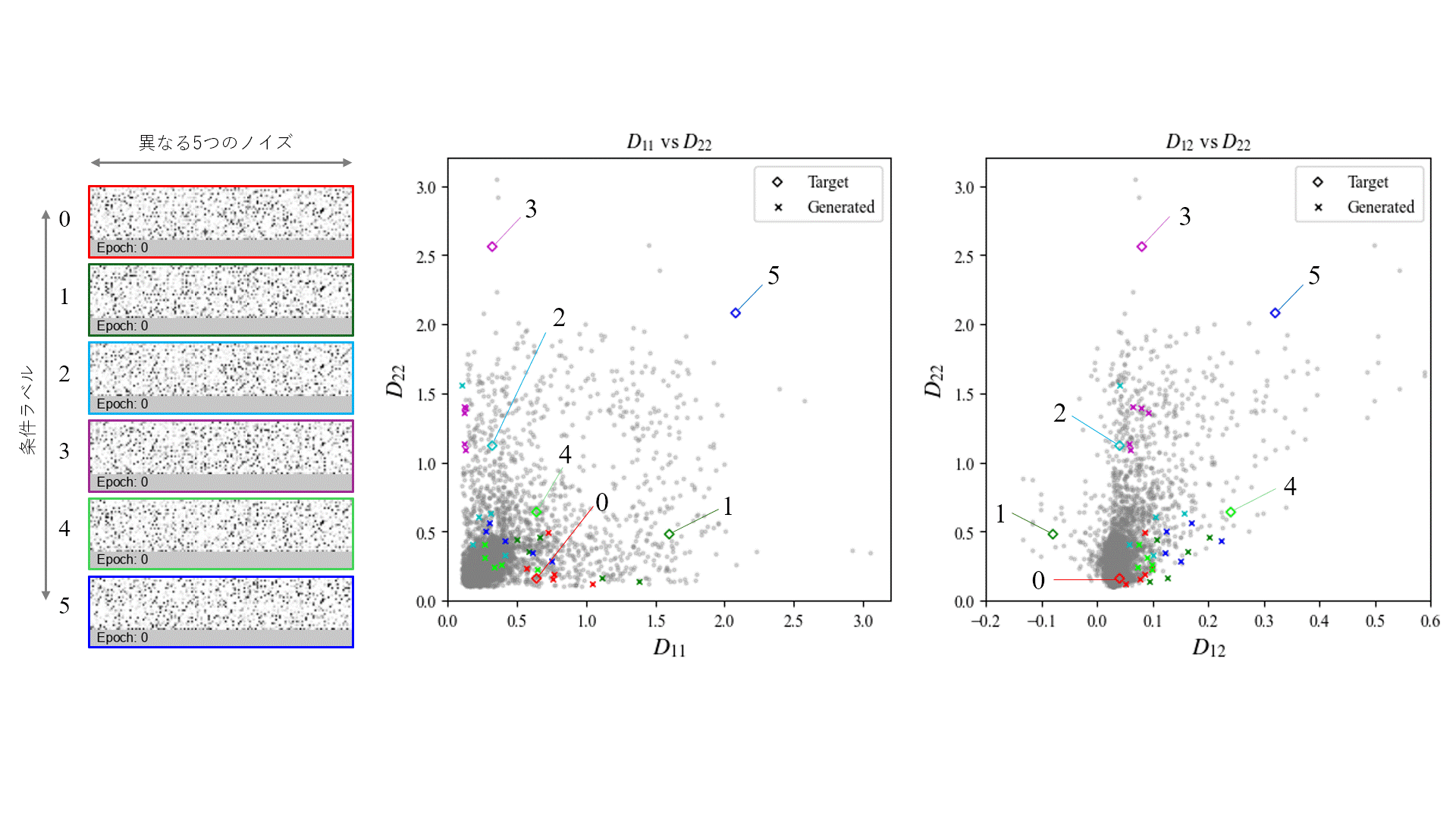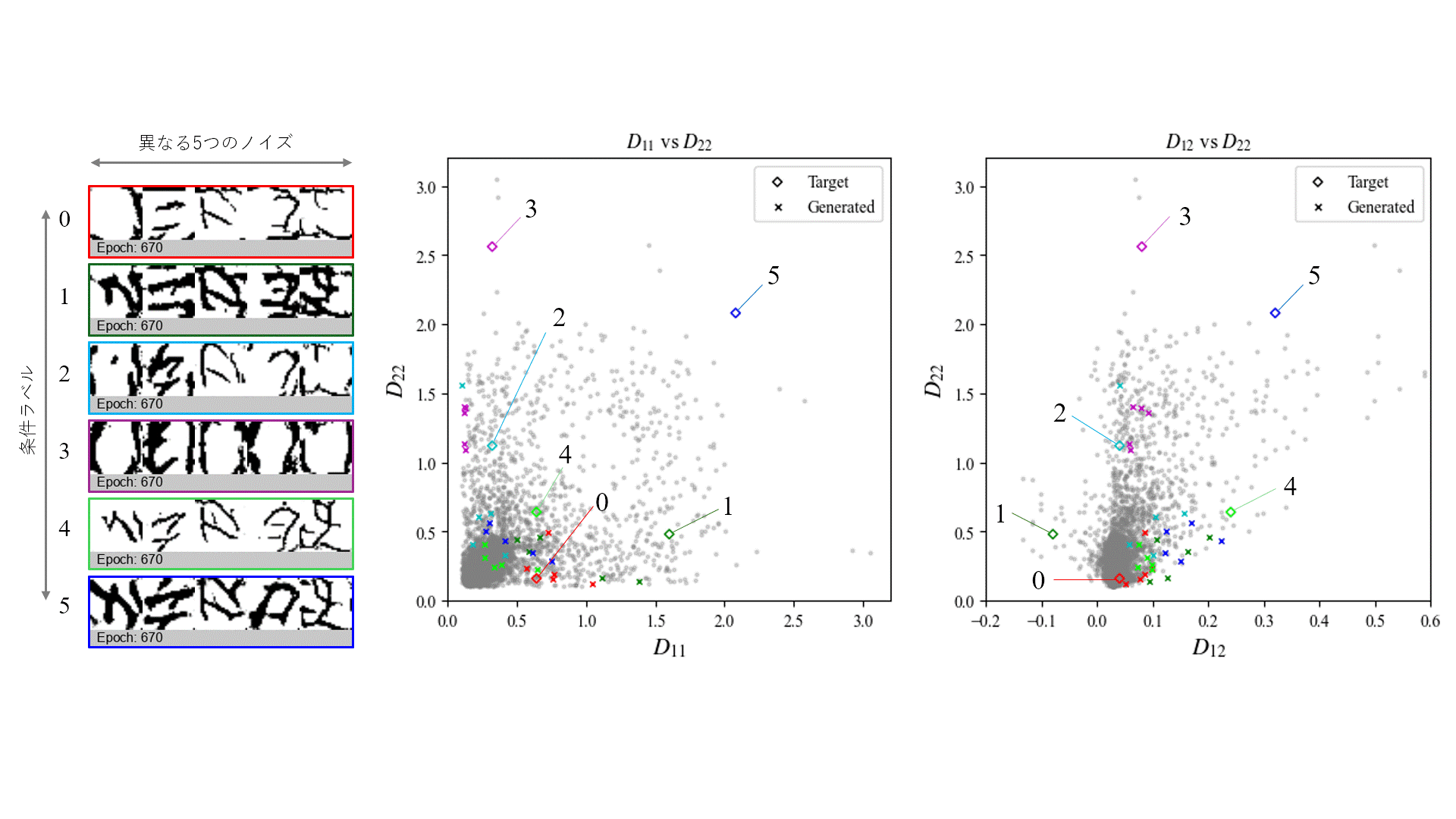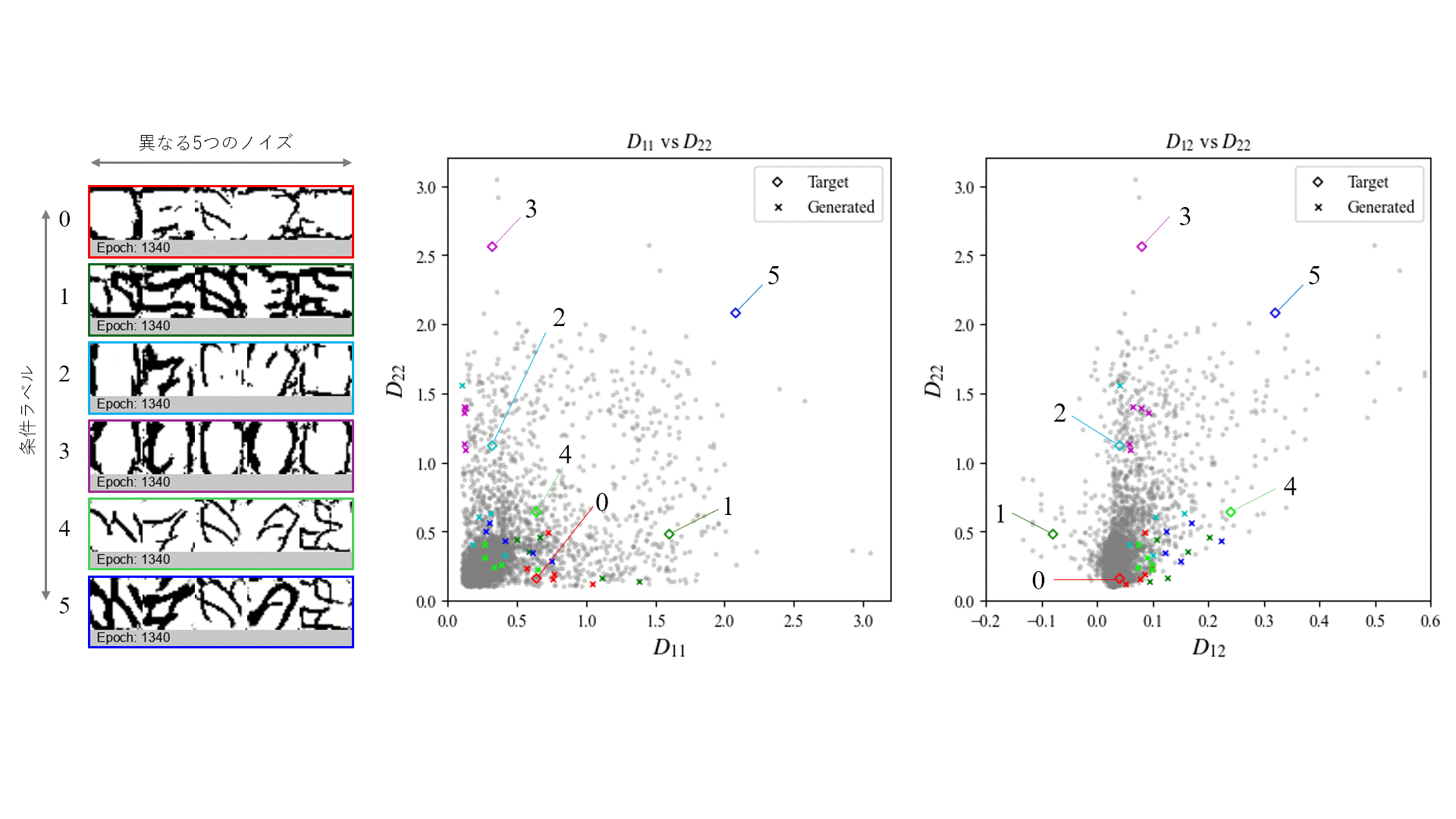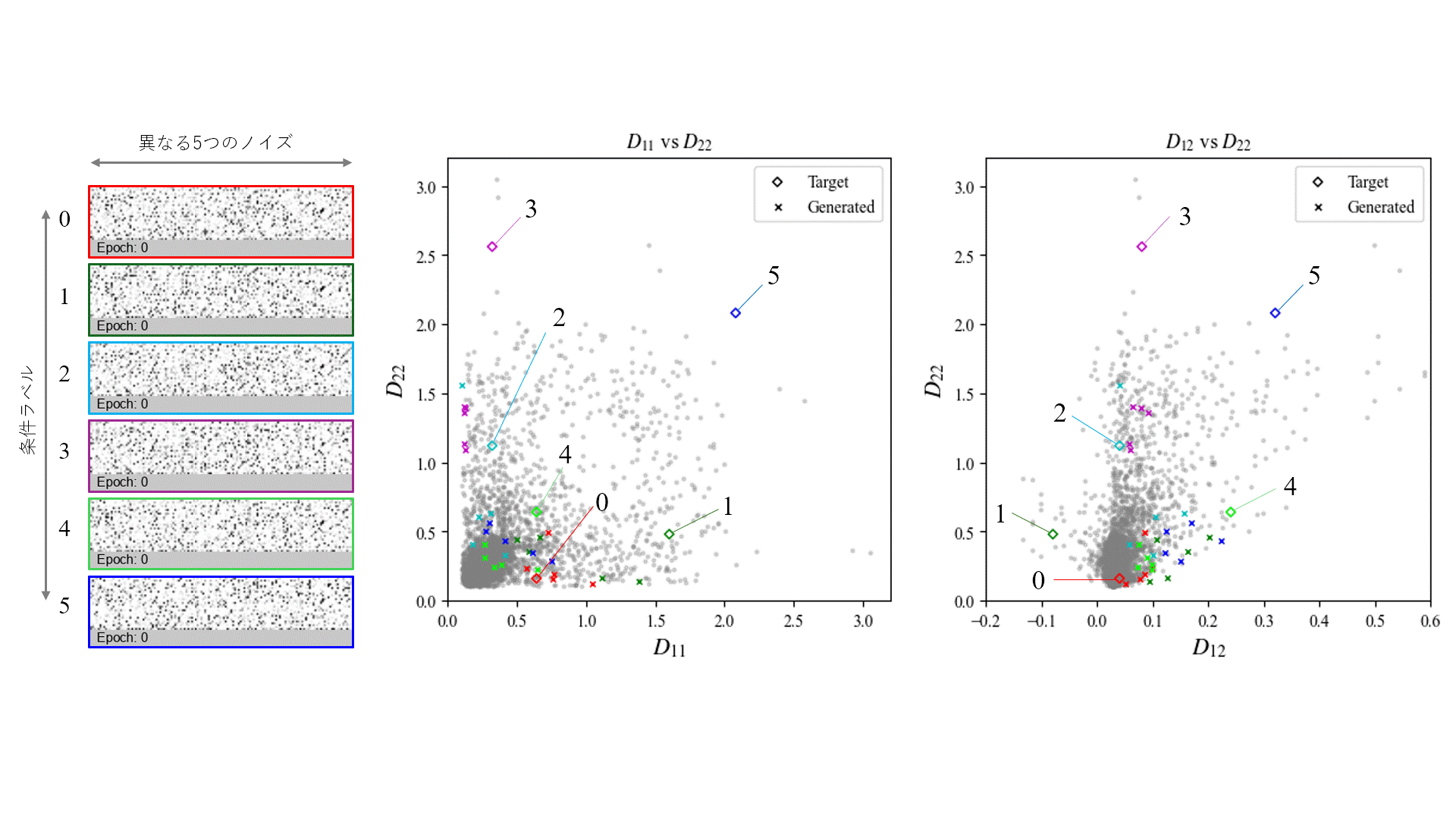
生成形状を見ると、強化する方向や剛性の大きさに応じた凹凸の大きさなど、ある程度指定条件に整合する構造形状となっていることが分かります。
一方で、色ごとに◇で示す条件ラベル値と×で示す生成結果の値を比較すると、学習データが少ない条件領域では条件忠実度が低い傾向がみられます。これは、モデルが既存データに類似した形状を生成するよう学習しているためであり、既存に存在しない条件に対応した形状を得るためには、新たなデータを加えた上で再学習を行う必要があると考えられます。
また、条件忠実度が高い条件領域でも、指定条件と生成形状との間には誤差が生じるため、現時点での実設計への応用にはなお課題が残ります。他の生成モデルの導入や、ニューラルネットワーク構造・ハイパーパラメータのより精緻な調整により、一定の改善が見込める可能性はあります。ただし、指定値により近い形状を生成するには、データセットの選別や最適化手法との併用といったアプローチが必要になると考えれます。

6. おわりに

機能条件から直接構造形状を導出する生成モデルの可能性を探るため、条件付きGAN（cGAN）を用いて検証を行いました。文字形状をもとに多様な板材凹凸形状のデータセットを作成し、曲げ剛性を指定した構造形状の生成を試みました。
結果として、曲げ剛性に応じた凹凸の方向や大きさなど、ある程度整合する形状を生成できており、単なる形状学習にとどまらず、機能を関連させた「もっともらしさ」を学習していることが示唆されました。

一方で、本手法は「形状パラメータの設定なく、誤差を許容しつつ条件を変えながら類似構造を生成する」といった場面では活用できそうなものの、実設計へ応用には次のような課題も明らかになりました：

• 専門的知識と労力が必要
  
  データセットの準備、ネットワーク設計、ハイパーパラメータの調整などに一定の知識と試行錯誤が求められます。
• 良い構造の生成には、良い構造が必要
  
  既存データに類似した形状を生成するため、未知条件領域では条件忠実性が低下します。
  
  また、本手法は最適化ではないため「求める機能になりそうな形状」であり「望ましい条件を満たす形状」や「機能の実現に必要な形状」を得ることができません。
  
  適切な構造形状を生成するためには、最適化結果を学習させる等、良質な形状をデータセットとする必要があります。

今回の検討を通じて、我々の最適化ベースの形状設計を超えるような「機能条件を入力するだけで適切な形状を自動生成する」生成モデルの実現には長い道のりがあることが分かりました。

形状設計に対する深層学習の適用可能性については継続的に検討しつつ、より高品質な形状生成を目指して取り組んでいきたいと思います。

英語版ではひらがなではなくアルファベットをデータセットに利用しています。データセットによる違いなど興味がある方は英語版と比較してみてください。（右下のENから変更できます。）

参考文献

本稿を執筆するにあたり、以下の文献を参考にしました。
[1] Xiaoyang Zheng et al. Controllable inverse design of auxetic metamaterials using deep learning. Materials & Design. 2021, 221, 110178
[2] Jan-Hendrik Bastek et al. Inverse design of nonlinear mechanical metamaterials via video denoising diffusion models, Nature Machine Intelligence. 2023, 5, 1446-1475