はじめに

以前の記事でも紹介したように、トポロジー最適化は人間が思いもよらないような設計の示唆を与えてくれるものであり、より良い製品を設計する上で有効な手法です。

トポロジー最適化手法の概要と比較 | Nature Architects inc.

トポロジー最適化では一般的に勾配法が用いられ、有限要素解析と感度解析を繰り返して材料分布を最適化します。

問題の規模にもよりますが、基本的にこの過程は計算コストが高い傾向にあります。

設計プロセス初期の探索段階では、あらかじめ定められた制約条件の下で最適解を求めるだけでなく、設計制約と性能のトレードオフも踏まえ、複数の条件における最適解を比較・検討する必要があります。

このとき、条件を変更した際に瞬時に応答できる能力は、設計の効率化や意思決定の迅速化に直結します。

こうした背景から、トポロジー最適化を瞬時に実行できる技術が求められています。

リアルタイムトポロジー最適化の概要

近年、トポロジー最適化を瞬時に実行する手法として、リアルタイムトポロジー最適化が注目を集めています。

リアルタイムトポロジー最適化とは、勾配法によるトポロジー最適化で事前に導き出した最適幾何形状と解析条件のデータセットを学習し、新たな条件に対しても反復計算を行うことなく最適幾何形状を予測できるモデルを構築する手法です。

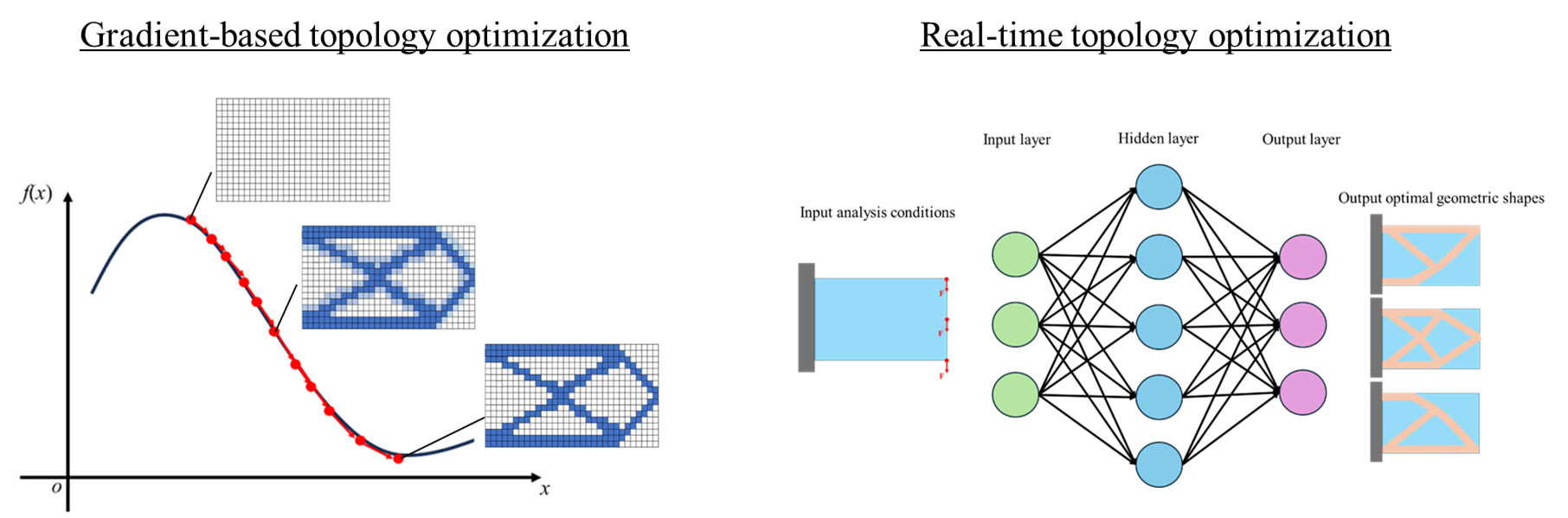
前述の通り、勾配法に基づくトポロジー最適化では各種計算が繰り返し必要なのに対し、リアルタイムトポロジー最適化では、一度データセットを用意して学習させてしまえば、ユーザーは所望の解析条件を予測モデルに入力するだけで瞬時に最適幾何形状に近しい材料分布を創出することができます。

以降で、より具体的に各種手法について見ていきます。

リアルタイムトポロジー最適化の具体的な手法

荷重を与える座標を学習データとする手法

最も単純なリアルタイムトポロジー最適化として、荷重を与える座標を変数として学習を行う手法[1]があります。

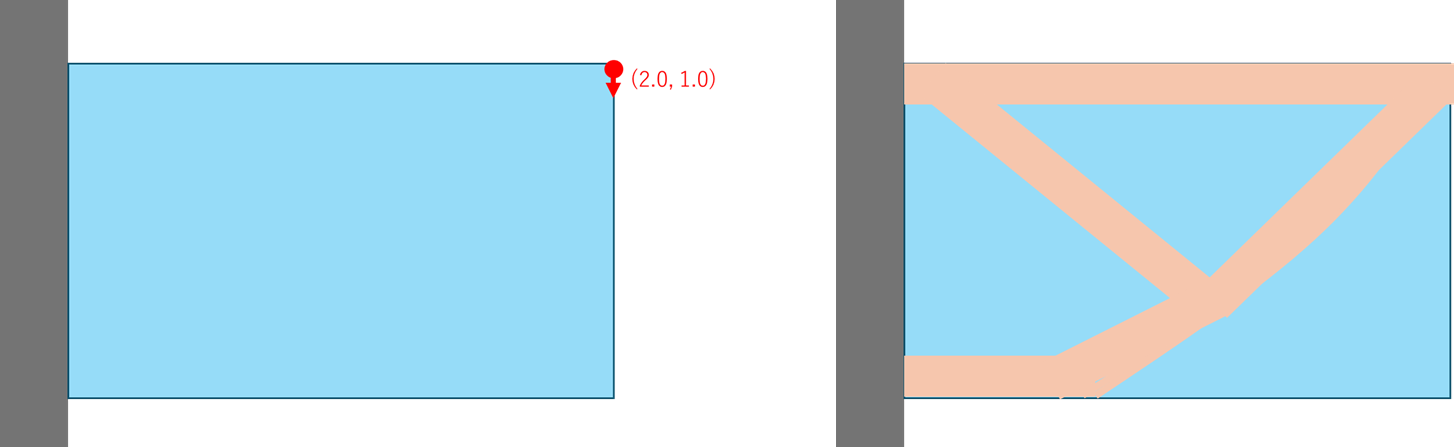
荷重を与える座標を1,2,...,N個目と動かしながら、各荷重点での最適幾何形状を勾配法によるトポロジー最適化によりサンプリングし、荷重を与える座標と最適幾何形状のセットを学習させます。

ユーザーは、学習済のモデルに所望の荷重点座標を入力すれば、それが未学習の荷重点であっても瞬時に最適幾何形状に近しい材料分布を出力することができます。

この生成モデルは、共通の固定境界条件・荷重角度に対して荷重座標のみを学習変数として扱うため、異なる境界条件や荷重方向には対応できない限定的なモデルと言えます。

初期物理場を学習データとする手法

実設計に活用できる手法に近づけるためには、多様な境界条件に対応できる汎化性能の高いモデルを構築する必要があります。

多様な境界条件に対応させるための手段として、各解析条件において設計領域が材料で満たされた状態での応力やひずみ分布等の物理場（以下、初期物理場)を学習データに用いる手法があります[2]。

初期物理場には、設計領域のどこにどのようにして変形が発生するのか　という設計にとって本質的な情報が連続場として含まれます。

創出したいのはまさにこの初期物理場が分布する領域をうまく支持する形状であり、荷重や固定境界条件を表す数値ラベル情報のような間接的データよりも効率的に学習でき、汎化性能の向上を期待できます。

ユーザーは、学習済のモデルに所望の問題設定における初期物理場を入力すれば、それが未学習の問題であっても瞬時に最適幾何形状に近しい材料分布を出力することができます。

Physics Informed Neural Networks (PINN)に基づく損失

従来のモデルは、解析条件と最適幾何形状の対応関係を学習するものであり、物理的な整合性を担保する要素は含まれていません。

そのため、固定点や荷重点に材料が存在しない、あるいは他の構造と接続されていない“浮き島”のような物理的に不整合な幾何形状が生成される可能性があります。

そこで、本研究では Physics-Informed Neural Networks (PINN)に基づく学習損失を導入します［3, 4］。

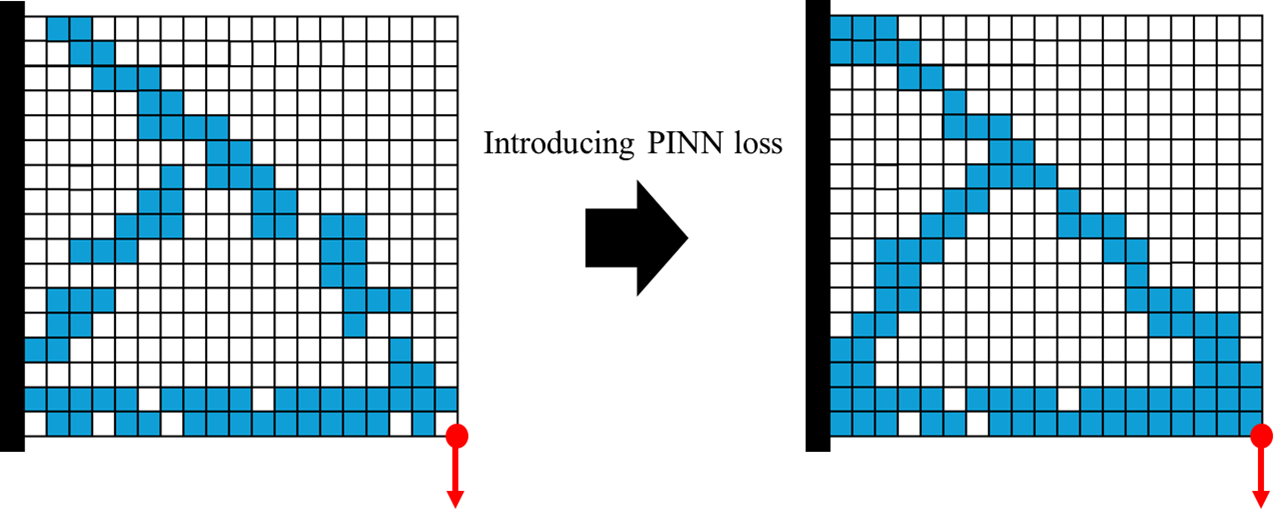
PINNとは、物理法則をニューラルネットワークの学習損失に組み込むことで、物理的妥当性を反映した学習を可能にする手法です。

問題設定に依存しない普遍的な物理法則を教師信号として利用することで、少ない学習データでも効率的に学習が進み、未知の解析条件に対する優れた汎化性能が期待されます。

ここでは、静的な剛性問題を例に説明します。

構造に作用する外力ベクトルを \boldsymbol{F} 、SIMP法により補間される密度依存の剛性マトリクスを \boldsymbol{K(ρ)}、変位ベクトルを \boldsymbol{u} としたとき、構造の平衡方程式は以下の式で表されます。

\boldsymbol{K(ρ)u} -\boldsymbol{F}=0

この式は、物理的に妥当な構造であれば常に満たされるべき基本的な力の釣り合い条件です。

本研究では、変位と密度をそれぞれ独立したニューラルネットワークで予測しており、この平衡方程式の残差 (PDE残差) |\boldsymbol{K(ρ)u} -\boldsymbol{F}|^2 を損失関数に導入します。

これにより、ネットワークは変位と密度の予測が物理法則を満たすように学習します。

さらに、固定境界における変位がゼロとなる境界条件を、変位予測ネットワークの損失関数として別途導入することで、平衡方程式残差を介して密度予測ネットワークにも固定境界の情報が間接的に伝達されます。

このように、サンプルデータだけに依存せず、物理的整合性を内部に備えたモデルを構築することが可能となり、学習の信頼性および汎化性能のさらなる向上が期待されます。

実際に行った学習

学習モデル概要

リアルタイムトポロジー最適化の学習には様々なネットワーク構造を用いた例がありますが、本記事では、GANの一種であるpix2pix[5]に基づくネットワークを用います。

以前の記事でもGANを用いて形状生成を行っておりますので是非ご一読ください。

条件付き生成ディープラーニングを用いた形状生成 | Nature Architects inc.

pix2pixとは、ある画像(例:ゴシック体風の文字）を、所望のスタイル（例:明朝体風の文字）に変換することが可能な画像から画像への変換モデルです。

pix2pixについてはウェブや専門書に数多く解説があるため、詳細は他をご参照ください。

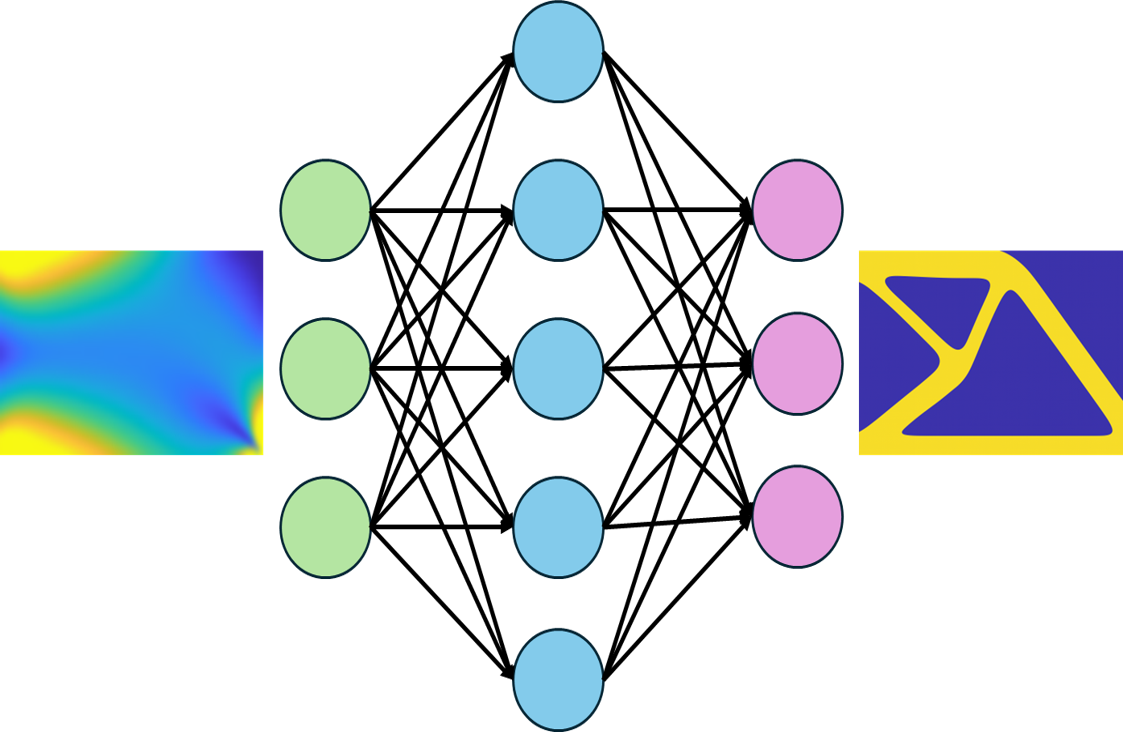
本記事では、予測モデルを初期物理場画像から最適幾何形状画像への画像変換モデルと捉えて学習を行うため、学習の際には以下のデータをネットワークに与えます。

〇入力側

初期ミーゼス応力分布画像

〇出力側

最適幾何形状画像

今回は簡易的検証のため入力データとしてミーゼス応力分布のみを用いています。 ミーゼス応力分布は向きの情報が欠落するため、予測精度や汎化性能を向上させたい場合、応力-応方向場やひずみエネルギ密度分布等との併用も考えられます。

学習の損失には、GAN損失、正解画像とのL1損失、PINN損失（平衡方程式残差および固定境界損失）、体積制約損失を用いました。

GAN損失により出力密度分布の本物らしさを、L1損失により正解データとの大局的な形状一致を、PINN損失により物理的な妥当性を、体積制約により材料使用量を学習します。

学習を行う解析条件

簡易的な実装のため、本記事では固定境界条件と荷重座標のみを学習変数として扱います。 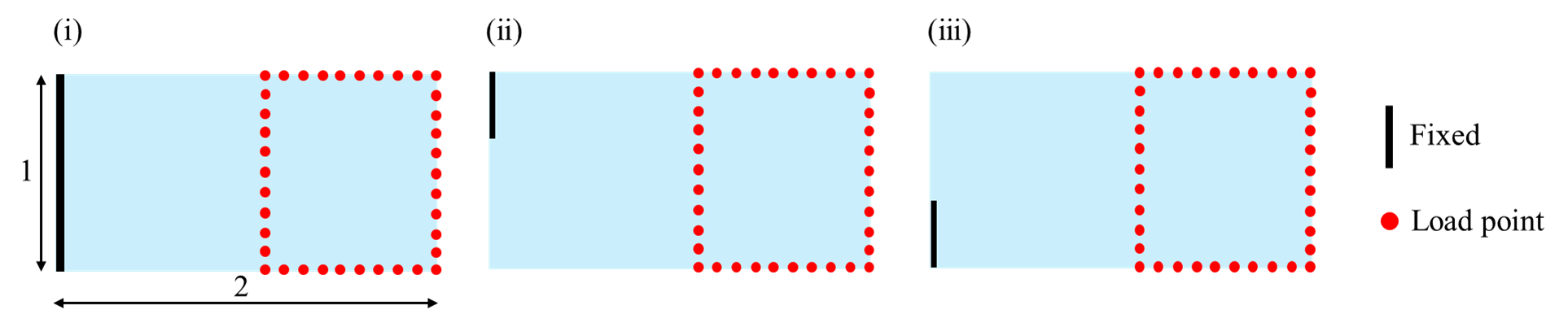上図に示すような(ⅰ)～(ⅲ)の3種類の固定境界条件において荷重座標を振って学習データのサンプリングを行います。

(ⅰ)左辺を全て固定し，1.0≦x≦2.0、0≦y≦1領域の外枠に0.1間隔で荷重点を設定

(ⅱ)左辺の上1/3を固定し，1.0≦x≦2.0、0≦y≦1領域の外枠に0.1間隔で荷重点を設定

(ⅲ)左辺の下1/3を固定し，1.0≦x≦2.0、0≦y≦1領域の外枠に0.1間隔で荷重点を設定

サンプリングしたデータ数は(ⅰ)～(ⅲ)合わせて114個で、これを左右反転させたデータも学習データに加えたため学習データ数は計228個です。

簡易的な検証のため少ないデータ数となっておりますが、実設計に利用する際にはより多様な条件下でデータサンプリングし、膨大なデータ数を扱うこととなります。

テストを行う解析条件

次に、(Ⅰ)～(Ⅲ)にテストを行う解析条件を示します。

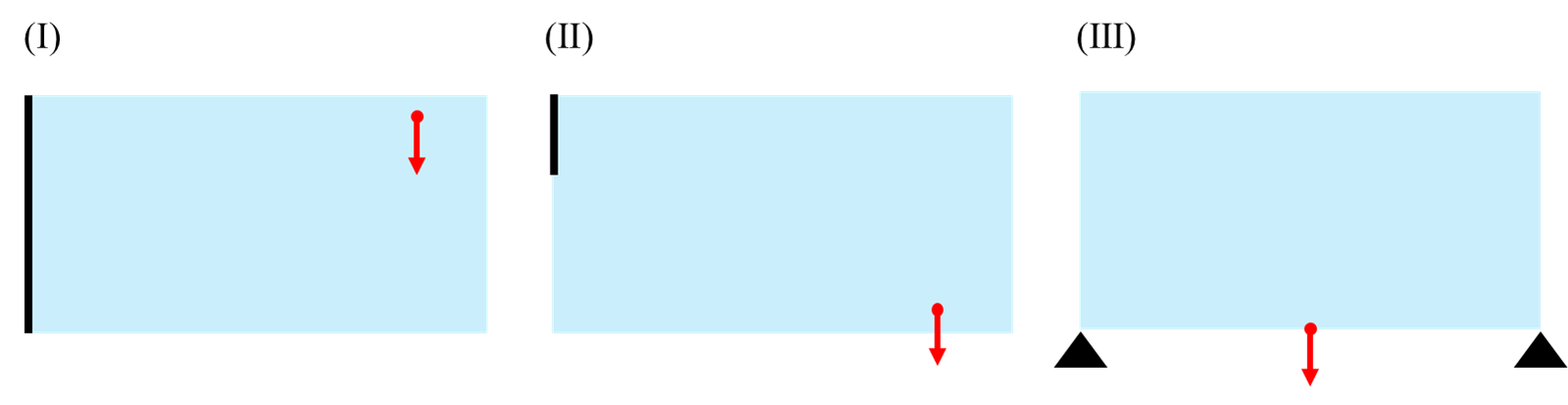
(Ⅰ)左辺を全て固定し、(1.7, 0.8)に鉛直下方向荷重を負荷

(Ⅱ)左辺の上1/3を固定し、(1.8, 0.1)に鉛直下方向荷重を負荷

(Ⅲ)下辺の両端を単純支持し、(1.0, 0)に鉛直下方向荷重を負荷

(Ⅰ)(Ⅱ)は既知の固定境界条件における予測結果、(Ⅲ)は未知の固定境界条件における予測結果の評価を目的としています。

リアルタイムトポロジー最適化結果

(Ⅰ)左辺を全て固定し(1.7, 0.8)に鉛直下方向荷重を負荷

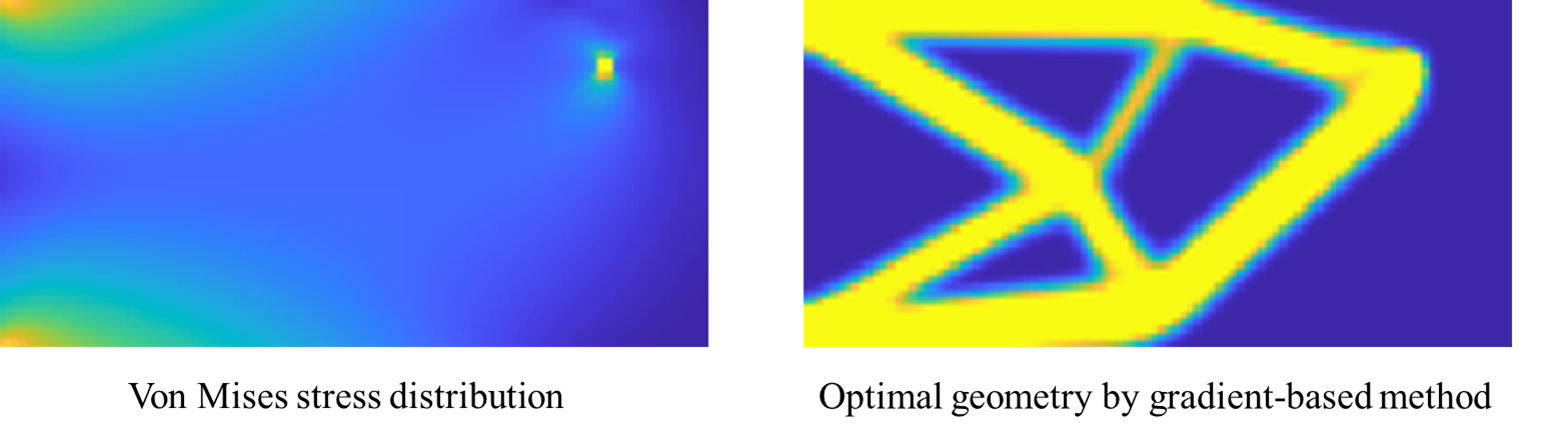
この問題設定における初期ミーゼス応力分布と勾配法による最適幾何形状、学習epochが進むごとの予測結果アニメーションを示します。

外形形状・内部のリブを正確に予測できており、両者の差異は各部材の太さや密度の濃さ程度で、非常に良く似た幾何形状であると言えます。

(Ⅱ)左辺の上1/3を固定し、(1.8, 0.1)に鉛直下方向荷重を負荷

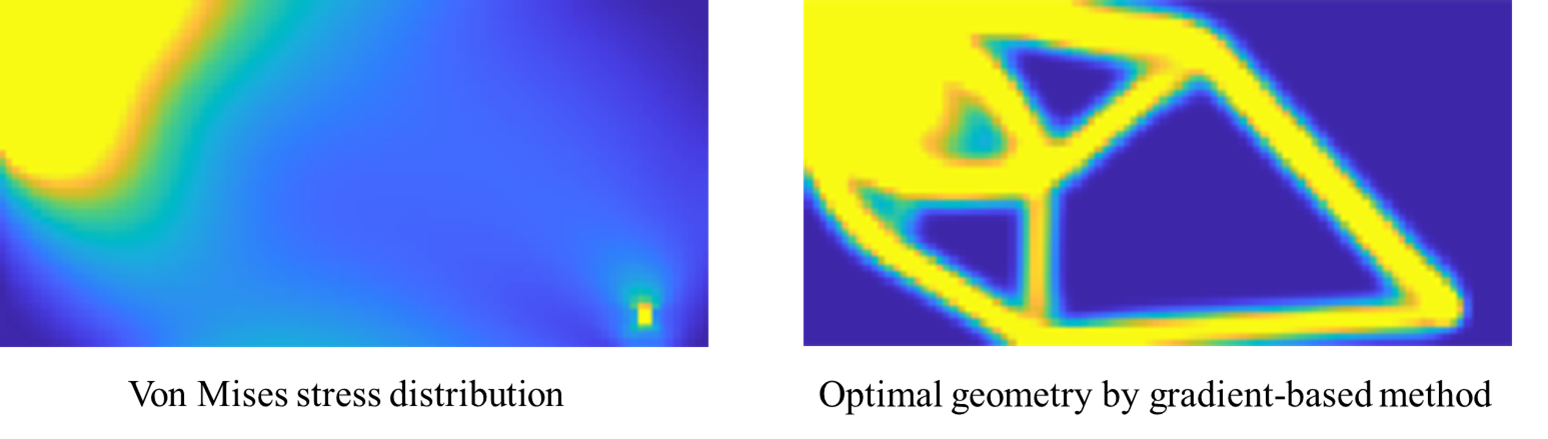
この問題設定における初期ミーゼス応力分布と勾配法による最適幾何形状、学習epochが進むごとの予測結果アニメーションを示します。

(Ⅰ)と同じく、外形形状・内部のリブを正確に予測できており、両者の差異は各部材の太さや密度の濃さ程度で非常に良く似た幾何形状であると言えます。

(Ⅲ)下辺の両端を単純支持し，(1, 0)に鉛直下方向荷重を負荷

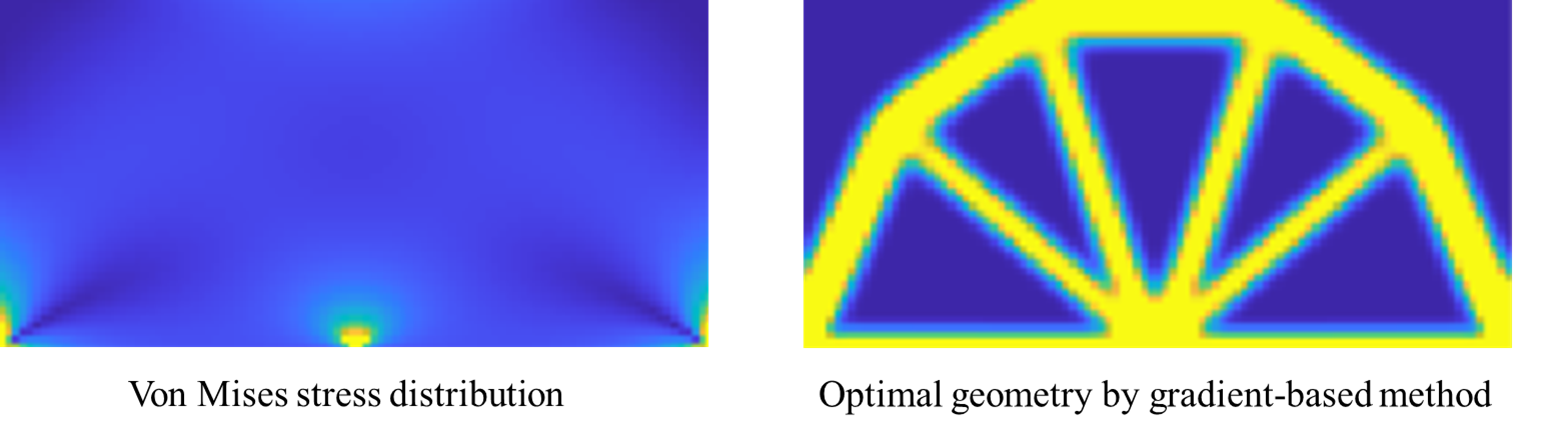
この問題設定における初期ミーゼス応力分布と勾配法による最適幾何形状、学習epochが進むごとの予測結果アニメーションを示します。

外形形状やリブの配置等を正確に予測はできていませんが、アーチ状の外形の中にV字のリブがあり荷重点を支持するという大まかな構造的特徴を予測することができています。

目的関数値の比較

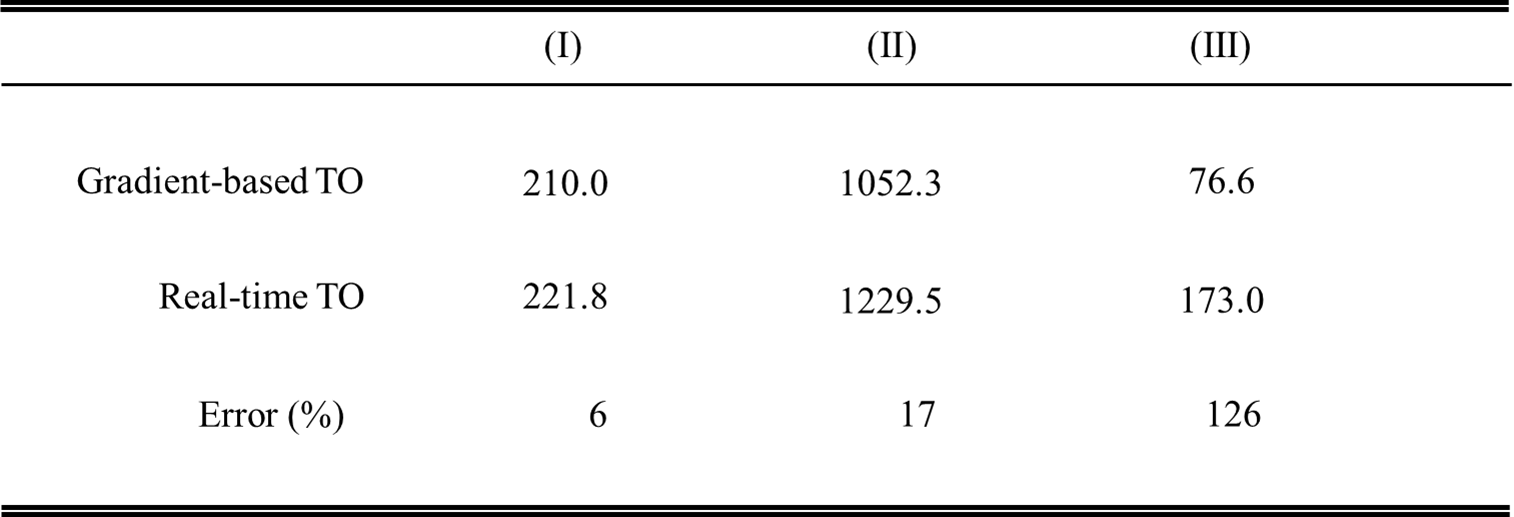
次に，(Ⅰ)～(Ⅲ)の勾配法とリアルタイムトポロジー最適化の目的関数値(平均コンプライアンス)を比較します．

(Ⅰ)(Ⅱ)から、既知の境界条件において、目的関数値は20%以下程度の誤差を含むことがあるとわかりました。

(Ⅲ)から、未知の境界条件においては、既知の境界条件に比べて誤差が増加してしまうことが確認されました。

しかしながら、荷重点や固定点に材料が存在しなかったり、幾何形状が不連続で構造全体が連結していないような、物理的に不整合な形状が生成された場合には、目的関数値が数十倍から数百倍以上に達することもあり得ます。

そのようなケースと比較すると、本手法は比較的良好な予測性能を有していると評価できます。

予測精度を向上させたい場合、荷重座標や境界条件ラベル、他の初期物理場画像等で入力データを補強したり、より多くの問題設定で学習データ数を拡充する必要があると考えられます。

計算時間の比較

次に、(Ⅰ)の解析条件において、勾配法にかかる計算時間と学習済の生成モデルによる予測にかかる時間を比較します。

勾配法に設計変数の更新幅に基づく停止条件を設けたところ55iterationで停止したため、その時点までを勾配法の計算時間としています。

計算時間比較結果は上の表のようになりました。

リアルタイムトポロジー最適化は、データサンプリングと学習が事前に必要なものの、ユーザーが実際に最適幾何形状を予測する段階ではほぼ瞬時に実行でき、勾配法との計算時間の差は歴然です。

おわりに

本記事では，トポロジー最適化を瞬時に行う技術である「リアルタイムトポロジー最適化」の概要を説明し，簡易的な実装を行うことで理解を深めました。

入力データに初期物理場を用いることやPINNの導入により効率的に学習でき、一定の汎化性能を得られることがわかりました．

一方で，リアルタイムトポロジー最適化には以下のようにいくつかの課題があります．

① データサンプリングの計算負荷

本記事では、計算コストの低い2次元線形静解析問題を対象としましたが、実設計では多くの場合、3次元かつ非線形な問題が扱われます。このような解析においては、学習用データの準備自体に膨大な計算コストがかかるため、効率的なサンプリング戦略やローフィデリティモデルの導入が不可欠となります。

② 学習対象変数の増加による学習難易度の上昇

実用設計においては、本研究で対象とした変数（荷重位置、固定位置）に加え、荷重の方向・大きさ、体積制約値、設計領域の形状や寸法など、設計条件が飛躍的に増加します。これにより、訓練データ空間が広がり、モデルがすべての組み合わせに対して安定して学習することが極めて困難になります。これらに対応するためには、学習データの工夫やネットワーク構造の高度化が課題となります。

③ 製造制約や応力制約といった複雑な実用制約への対応

現実の構造設計では、最小肉厚、応力上限、製造可能性、穴空け禁止領域など、複雑かつ厳格な設計制約が多く課されます。これらの制約は問題依存性が高く、一般化された形で学習に組み込むことが難しいため、予測結果にそれらを厳密に反映するのは現時点では困難です。

以上の理由から、リアルタイムトポロジー最適化のみで完全な最適解を一度に得ることは困難であり、現状では以下のような ハイブリッドアプローチ が現実的です。

ステップ1：リアルタイム予測モデルで初期設計案を瞬時に生成

ステップ2：その初期案を初期値として勾配法等の最適化手法を適用

このように、条件変更への即応性能と最終精度のバランスを取る設計フローを導入することで、実用設計においても現実的かつ高効率な最適化が実現可能になると考えられます。

皆さんもリアルタイムトポロジー最適化を実装し、試行錯誤してみてください。理解が深まり、新たな発見があることと思います。

参考文献

[1] Lei, X., Liu, C., Du, Z., Zhang, W., and Guo, X., “Machine Learning-Driven Real-Time Topology Optimization Under Moving Morphable Components-Based Framework,” Journal of Applied Mechanics, Vol. 86, No. 1, 2019, p. 011004.

[2] Nie, Z., Lin, T., Jiang, H., and Kara, L. B., “TopologyGAN: Topology Optimization Using Generative Adversarial Networks Based on Physical Fields Over the Initial Domain,” arXiv preprint arXiv:2003.04685, 2020

[3] Jeong, H., Batuwatta-Gamage, C., Bai, J.,　Xie, Y. M., Rathnayaka, C., Zhou, Y., and Gu, Y. T., “A complete Physics-Informed Neural Network-based framework for structural topology optimization,” Computer Methods in Applied Mechanics and Engineering, Vol. 417, Part A, 2023, p. 116401.

[4] Yin, J., Wen, Z., Li, S., Zhang, Y., and Wang, H., “Dynamically configured physics-informed neural network in topology optimization applications,” Computer Methods in Applied Mechanics and Engineering, Vol. 426, No. 1, 2024, p. 117004.

[5] Isola, P., Zhu, J. Y., Zhou, T., and Efros, A. A. "Image-to-image translation with conditional adversarial networks." IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 1125–1134.