概要

(文章:大嶋, 設計:夏目)
この記事ではNature Architectsが行う材料代替設計の事例について紹介します。材料代替設計といえば車載の金属部材を樹脂化(エンプラ化)することで軽量化・低コスト化を実現するものが一般的です。これとは別にステンレスなどの複数の金属部材をアルミで一体化し軽量化を実現するなど樹脂化以外にも様々な材料代替設計がありえます。
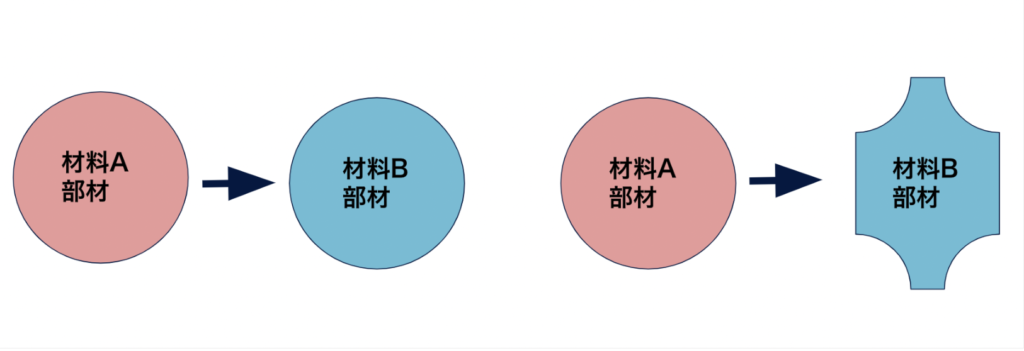
材料代替設計では材料Aの部材の形状を材料Bに代替するだけでは必要な機能要件(例えば剛性、振動特性、熱特性など)が損なわれてしまう場合が少なくありません(下図)。従って材料を変更した際に必要とされる機能要件を満たす形状に再設計する必要があります。
このような材料代替設計では機能、材料、製造制約、形状を包括的に考慮した設計が必要となります。Nature Architectsではこうした設計を独自の設計技術DFM(Direct Functional Modeling)を活用して実現しています。
今回は、金属から樹脂への材料代替設計ではなく少し変わった、軟質樹脂から硬質樹脂(PP、POMなど)への材料代替設計を紹介します。柔軟材料の変形を硬質樹脂で生み出すために必要な剛性を波板形状を最適に設計し材料代替を実現しました。この材料代替によって、低コストか、軽量化、環境負荷低減を可能にします。
ゴム・エラストマーを硬質樹脂化するメリット
ゴムやエラストマーを硬質樹脂化するメリットは安価な材料へ代替することによるコスト削減だけではなく、体積削減による軽量化のメリットが見込まれます。一方、柔軟材料が持つ低剛性・許容変形を硬質樹脂で実現するためには、必要な剛性と応力分散を実現する形状に再設計する必要があります。
Nature Architectsの設計技術:DFMを活用することで硬質樹脂に下図にあるコルゲーション(波形状)を最適設計することで硬質樹脂でも応力を分散・低減し許容変形や剛性をコントロールする設計が可能です。

今回はこのコルゲーションを用いて、硬質樹脂部材の使用時(特定の境界条件)で必要な剛性低減・応力分散を実現し柔軟材料から硬質樹脂への材料代替を可能にし、結果として既存部材を低コスト化、軽量化を実現しました。
設計手法
<問題のセットアップ>
今回はある対象物を保護する部材としてラジエーターファンカバーの形状を*ベンチマーク形状として設計を行います。ラジエーターファンカバーの表面にコルゲーション(波形状)を設計し応力緩和(最大応力を最小化)する問題を考え、許容応力の範囲内で所望の変形を実現する構造を探索します。
(※ラジエーターファンカバーはベンチマーク形状で実務で扱う保護部材の形状とは異なります)
<モデル形状>
一般的なラジエーターファンカバーの形状を対象とする。

<設計変数>
上記の図の上下にある円形と矩形のラインを断面にしたスイープによって間に面を張ることで対象とする形状を生成。コントロールポイントは次のように設定しました。
- 境界部の曲線を各13分割しLINEを引きます。
- LINEの内側を5点とり、5×13本=65点がパラメーターで各点における曲面の法線方向に-10.0〜+10.0 の範囲で値を取れるようにします。
- 13本それぞれに5点(境界を入れれば7点)を通る曲線を定義します。
- 生成した13本の曲線をスイープし曲面を定義します。
- 面の法線方向に点を上下させることでコルゲート構造(波形状)を生み出すことができます。
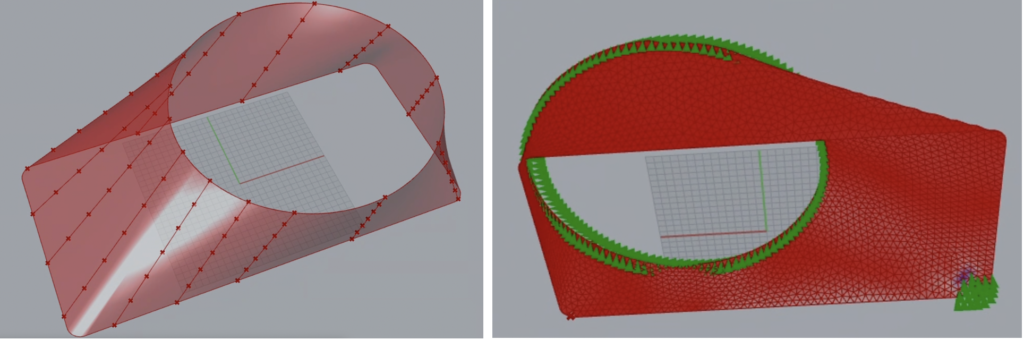
<境界条件/目的関数>
境界条件はファンがある丸い部分を変位固定し、右下隅または左上隅に対して強制変位を与える解析を実行しました。目的関数は応力最小化問題とします。上図の右下に強制変位を加えた場合での応力最小化問題を解きます。
<最適設計>
どんな最適化手法を用いたか?
形状最適化にはベイズ最適化の手法の一つであるTPE(Tree-structured Parzen Estimator)を使用しています。
なぜその手法を用いたのか?
多目的最適化だと遺伝的アルゴリズム(GA)が良く知られています。GAの場合、世代ごとに(例えば50回の評価に1回)勾配に相当するものを計算するため収束するまで計算量が多くなることがよくあります。
近年では機械学習などの1回の評価の計算コストが高いもののパラメーターの最適化はベイズ最適化のような SMBO(Sequential Model-Based Global Optimization) と呼ばれる手法が使われる場合が多いです。SMBOはこれまで得られた観測点から目的関数の値が改善される確率の高い点を次の観測点にする手法のためGAに対して収束が早い場合があります。
ベイズ最適化は1回の評価のコストが高い構造解析でも有効で、今回はその手法の一つであるTree-Structured Parzen Estimator (TPE)を選択しました。ベイズ最適化の手法としてはガウス過程回帰を使った手法の方がより一般的ですが、本問題では変数の数が多いため十分なサロゲートモデルを作成するための評価点が多く必要でありサロゲートモデルの計算コストが高くなります。そのためガウス過程回帰を用いたベイズ最適化に対してサロゲートモデルの計算コストの低いTPEを使用しました。
設計結果(単一目的関数)
多目的最適化を実施する前に、上記ケースとは別の荷重ケースに対して単一目的最適化を行って形状の傾向を確認する。以下のように左上角に斜めから強制変位荷重をかけます。コルゲーション(波形状)を最適設計する前の形状では以下のような相当応力分布になった。最大相当応力は 389MPa。最適化した形状は以下となりました。
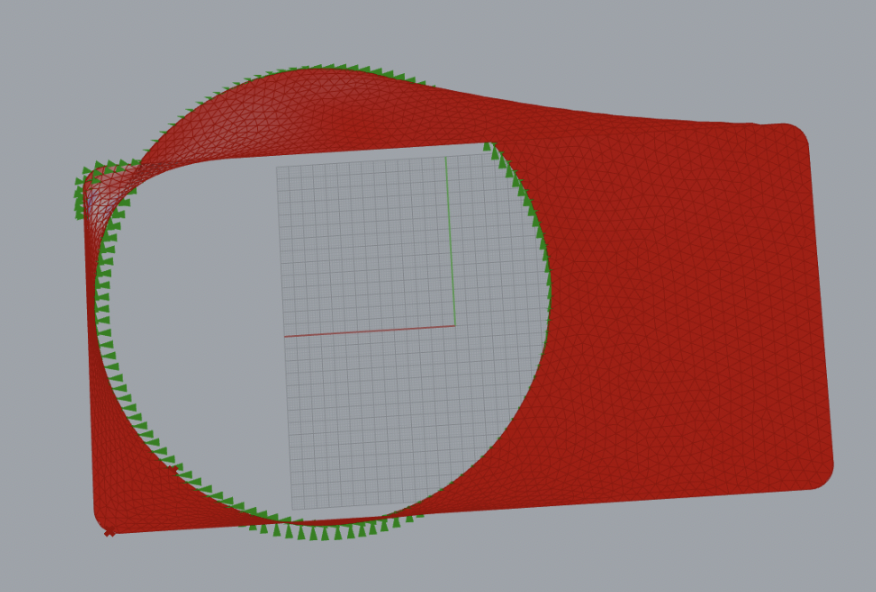

最適化形状では最大相当応力は 90.9MPaで、コルゲーションを与える前に比べて 約1/5と大幅な応力低減することができました。応力状態は下図のようになりました。

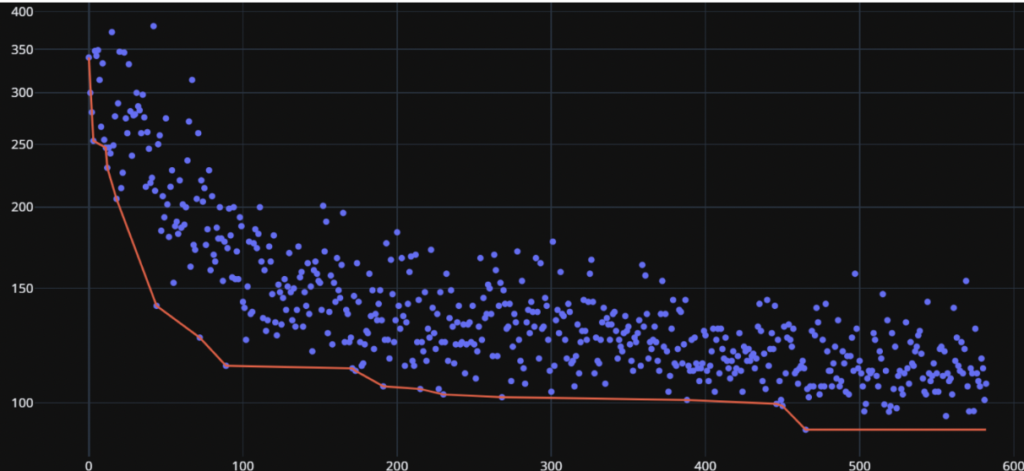
収束状況は以下通りです。
設計結果(多目的関数)
これまでは特定の荷重条件で最大応力を最小化する問題を解いてきました。より実用的には複数の荷重条件で最大応力を最小化する問題を解きパレート面上で設計要件をよりよく満たす解を探索することになります。今回は多目的関数の最適化は紹介しませんが、こうした多目的関数の最適設計も弊社では実務で取り組んでいます。
まとめ
今回は柔軟材料による保護部材を硬質樹脂化することで、コスト削減・軽量化を実現した設計を紹介しました。材料代替設計は多くの場合、設計要件を満たすように代替後の部材を再設計する必要があります。
Nature Architectsの設計技術DFMを活用することで、目的の機能を実現する形状、材料、製造方法を横断的に最適に設計することができます。これにより材料代替設計を迅速かつ効果的に実現したり、設計困難な材料代替設計を可能にします。
問い合わせ
Nature Architectsでは形状・機能・材料選定・製造条件を横断した付加価値の高い設計/設計支援を行っています。こうした設計に興味があるメーカー企業の方々は気軽にお問い合わせください。また弊社では業務改題につきフルタイムまたは業務委託のエンジニアを募集しています。こちらも気軽にお問い合わせください。

