概要
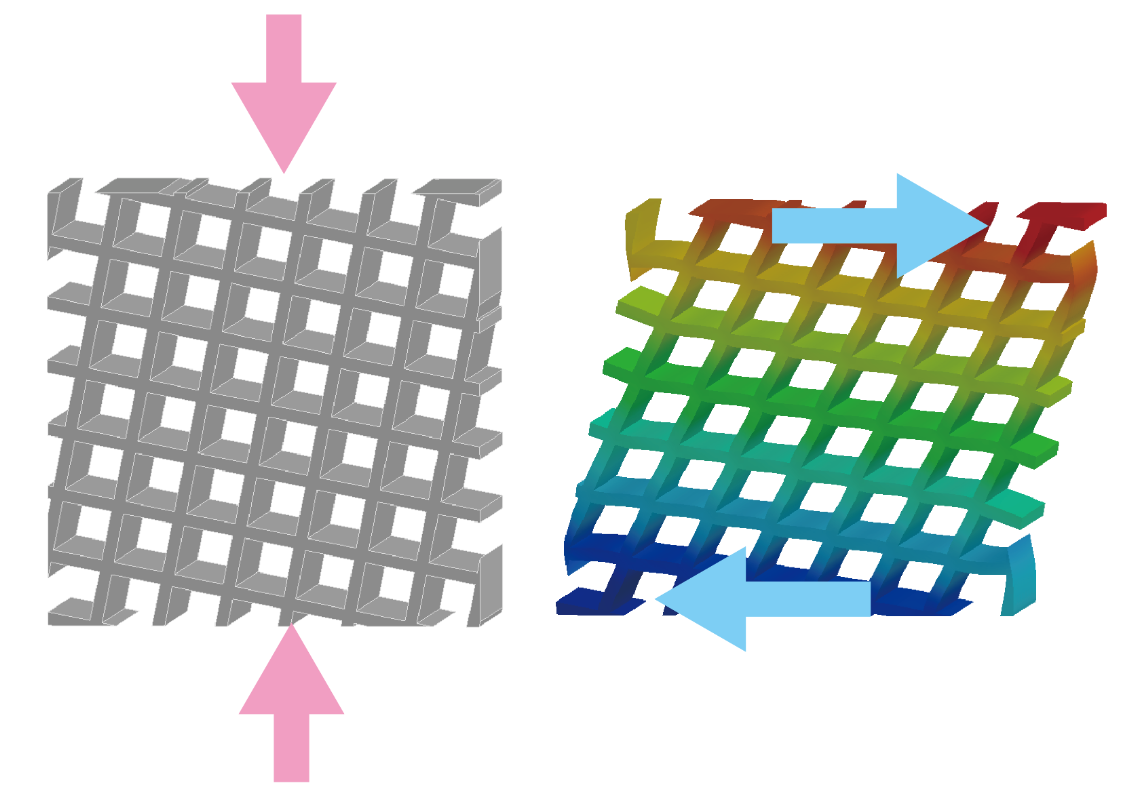
ミッドソールに3Dプリントされた特殊な構造が埋め込まれたアディダスのシューズ「4DFWD」は踏み込み力を推進力に変換する機能を持ちます。本記事ではこの機能を圧縮をせん断に変換するメカニカルメタマテリアルとして解釈し、その設計方法を解説します。
本記事は以下の3部構成のうち2つ目について解説します。
(2) 圧縮をせん断に変換するメカニカルメタマテリアルの設計
(3) 踏み込み力を推進力に変換するミッドソールの設計
圧縮応力をせん断ひずみに変換する材料物性値S_{32}
前回の記事では圧縮応力がせん断ひずみに変換される材料物性を2次元線形弾性構成則の観点から説明し、それはコンプライアンス行列\mathbf{S}(\theta)の(3,2)成分S(\theta)_{32}であることを明らかにしました。この値は材料の回転角度\thetaを用いて以下のようにあらわされました。
S(\theta)_{32} = \sin{4\theta}\cdot\frac{1}{4}\left(\frac{1}{G} - \frac{2(1+\nu)}{E}\right) = S(\theta)_{ang} \times S_{mat}\tag{1-1}ここでS(\theta)_{32}は回転角に関する項S(\theta)_{ang}と材料特性に関する項S_{mat}に分離されました。
S(\theta)_{ang} = \sin{4\theta}, \quad S_{mat} = \frac{1}{4}\left(\frac{1}{G} - \frac{2(1+\nu)}{E}\right)\tag{1-2}よってS(\theta)_{32}の最大化は回転角度・材料特性それぞれ独立に行うことができます。
S(\theta)_{ang}の最大化
S(\theta)_{ang}の最大化は簡単で、回転角\thetaが22.5^\circの時最大値1を取ります。よってこのときS(\theta)_{32}=S_{mat}が成り立ちます。
S_{mat}の最大化
等方材料であるとき、この値は0となります。この値の絶対値を大きくするためには、ヤング率Eとせん断率Gの比が大きく、または小さくする必要があります。すなわち
E>>G, \quad \text{or} \quad E<<G \tag{1-3}であるときに圧縮応力がせん断ひずみに大きく変換されます。
それではそのような材料物性を持つユニットセルはどのようなものが考えられるでしょうか?
以下では
- ヤング率
Eが低くせん断率Gが高いXラティス - ヤング率
Eが高くせん断率Gが低い+ラティス
の2例を紹介します。
ユニットセルの均質化
それぞれのラティスを紹介する前に、まずラティスを均質な材料とみなしたときの等価なコンプライアンス行列Sの計算方法である均質化法[1][2]をざっくり紹介します。
均質化法は以下のように周期構造であるラティスのユニットセルを取り出し、それを均質な材料として捉える手法です。
そのマクロコンプライアンス行列\mathbf{S}_{macro}は下図のようにユニットセルにそれぞれマクロ応力\sigma_x, \sigma_y, \gamma_{xy}を与え、
対応するマクロひずみ\boldsymbol\varepsilon_{\sigma_x}, \boldsymbol\varepsilon_{\sigma_y}, \boldsymbol\varepsilon_{\gamma_xy}を計算します。
このときユニットセルの境界面には周期境界条件を付与し、周期的な変形をするように拘束します。
そしてそれらを以下のように並べることでマクロコンプライアンス行列を求めます。
\mathbf{S}_{macro}=
\left[
\frac{\boldsymbol\varepsilon_{\sigma_x}}{\sigma_x} \quad
\frac{\boldsymbol\varepsilon_{\sigma_y}}{\sigma_y} \quad
\frac{\boldsymbol\varepsilon_{\gamma_{xy}}}{\gamma_{xy}}
\right]
\tag{2-1}こうして求めたマクロコンプライアンス行列からマクロヤング率E_{macro}、マクロせん断率G_{macro}、マクロポアソン比\nu_{macro}を求めます。
今回は形状がXZ平面とYZ平面での鏡映対称性、90°回転対称性があるためマクロ線形弾性材料は正方異方性のクラスに分類されることから、以下のように求めることができます。
E_{macro}=\frac{1}{S_{macro,11}},\quad G_{macro}=\frac{1}{S_{macro,33}},\quad \nu_{macro}=-\frac{S_{macro,12}}{S_{macro,11}}
\tag{2-2}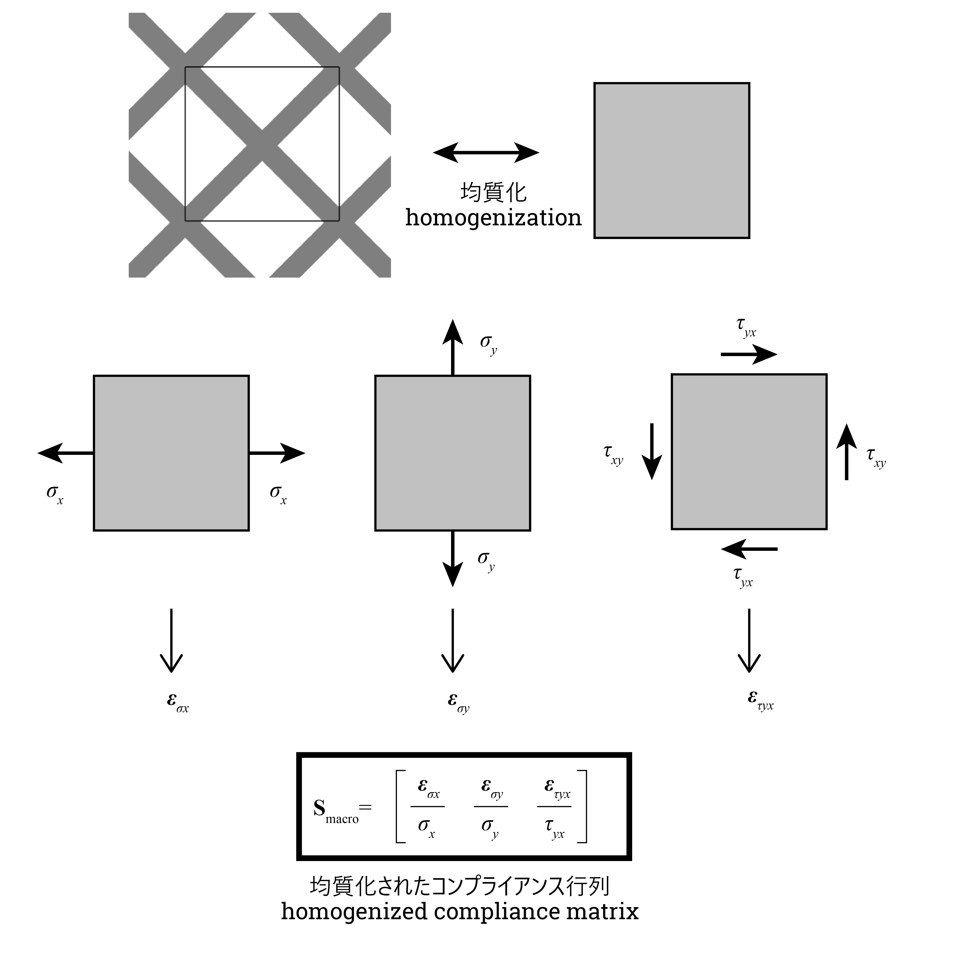
ヤング率Eが低くせん断率Gが高いXラティス
それでは具体的なラティスのマクロ物性値を均質化法を用いて計測していきます。

上図のようなXを敷き詰めたような格子構造(以下Xラティス)は
- 引張圧縮力に対して梁の曲げで変形し
- せん断力に対して梁の軸力で耐える
ため、ユニットセルの材料物性は
- マクロヤング率
E_{macro}:低 - マクロせん断率
G_{macro}:高
となると予想されます。
Carbon社の光造形用樹脂EPU40
ヤング率:8\text{[MPa]}
ポアソン比:0.5
を想定し
ユニットサイズを10/\sqrt{2}\text{[mm]}、板厚を1\text{[mm]}とした場合このユニットセルのマクロ材料物性を均質化法を用いて実際に計測したところ
E_{macro}=0.210\text{[MPa]}G_{macro}=0.904\text{[MPa]}\nu_{macro}=0.890
となりました。予想通りマクロヤング率に対してマクロせん断率が高くなりました。また、面白いことにマクロポアソン比が約0.9と通常の材料と比較して非常に高い値を示しました。S_{mat}は式\text{(1-2)}から以下となりました。
S_{mat} = -4.22\text{[1/MPa]} \tag{3-1}例えば\theta=22.5°で回転させると
S(\theta)_{32}=1.0\times(-4.22)=-4.22 \tag{3-2}となり、また前回記事式\text{(2-1)}より以下のように圧縮力を正の向きのせん断変形に変換することがわかります。
\gamma_{xy} = S(\theta)_{32}\times(-\sigma_y)=4.22\sigma_y \tag{3-3}ヤング率Eが高くせん断率Gが低い+ラティス

上図のような+を敷き詰めたような格子構造(以下+格子構造)は
- 引張圧縮力に対して梁の軸力で耐え
- せん断力に対して梁の曲げで変形する
ため、ユニットセルの材料物性は
- マクロヤング率
E_{macro}:低 - マクロせん断率
G_{macro}:高
となると予想されます。
同様にEPU40を用いてときの
ユニットサイズを5\text{[mm]}、板厚を1\text{[mm]}とした場合このユニットセルのマクロ材料物性を均質化法を用いて実際に計測したところ
E_{macro}=1.854\text{[MPa]}G_{macro}=0.055\text{[MPa]}\nu_{macro}=0.027
となりました。予想通りマクロヤング率に対してマクロせん断率が低くなりました。また、面白いことにマクロポアソン比が約0とコルク材料のような低い値を示しました。S_{mat}は式\text{(1-2)}から以下となりました。
S_{mat} = 4.29\text{[1/MPa]} \tag{3-4}例えば\theta=22.5°で回転させると
S(\theta)_{32}=1.0\times(4.29)=4.29 \tag{3-5}となり、また前回記事式\text{(2-1)}より以下のように圧縮力を負の向きのせん断変形に変換することがわかります。
\gamma_{xy} = S(\theta)_{32}\times(-\sigma_y)=-4.29\sigma_y \tag{3-6}式\text{(3-3)}と比較すると符号が逆転して大きさはほぼ同じであることがわかります。
よってXラティスと+ラティスの間には何かしらの関係性があると推察されます。
Xラティスと+ラティスの関係性
上で紹介した2つのラティスは、実は45°回転させるとぴったり重なり、同じラティスであるということができます。
当然ながらマクロコンプライアンス行列も45°回転させるとほぼ一致します。
また、Xラティスと+ラティスをそれぞれ22.5°回転させたラティスは下図のようになり、鏡映対称の関係となっています。

よってXラティス・+ラティスの圧縮-せん断成分S(\theta)_{32}が式\text{(3-2)}, \text{(3-5)}よりそれぞれ符号が逆転して大きさが同じである理由がこの幾何学的な対称性によることがわかります。
数値シミュレーションによる変形特性の確認
セットアップ
実際に圧縮力がせん断変形に変換されるか、数値シミュレーションを用いて確かめます。
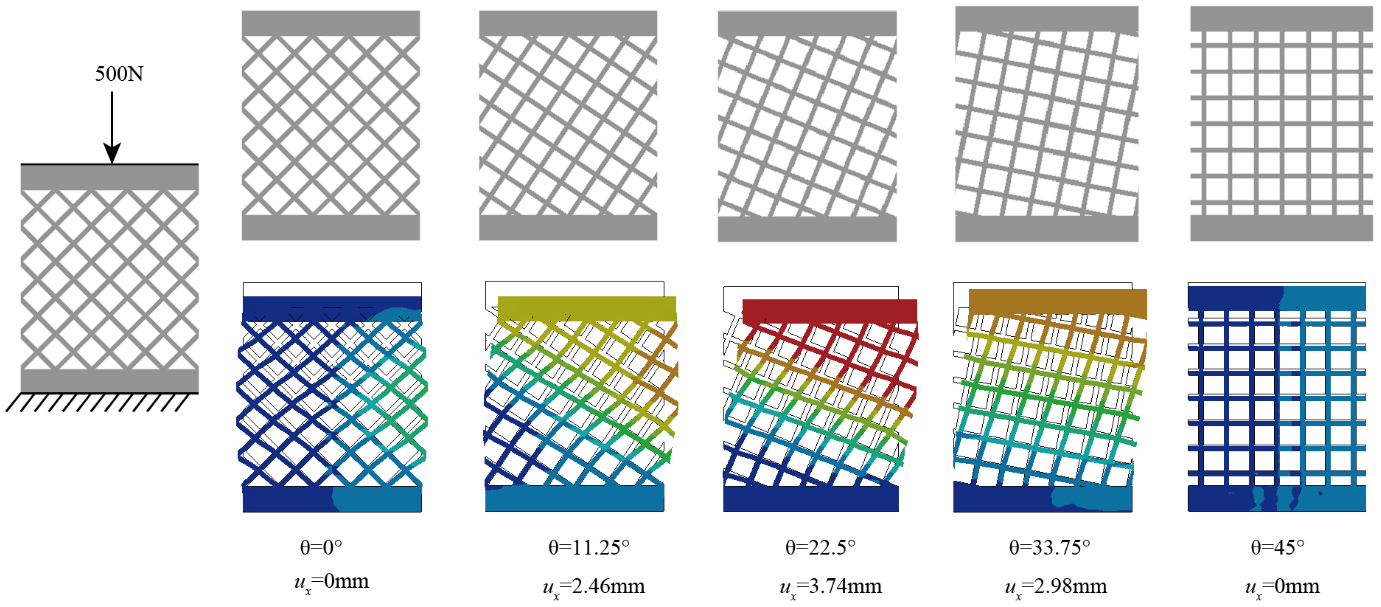
対象形状はXラティスとし、上面と下面に剛体ブロックを接続、下面固定、上面に下向き500Nの力をかけ、上面が横変位u_xを計測します。解析手法は簡易的に線形静解析としています。
回転角度は\theta = 0^\circ, 11.25^\circ, 22.5^\circ, 33.75^\circ, 45^\circとしました。
\theta=45^\circのとき、+ラティスと同一形状となります。
結果
\theta=0^\circ, 45^\circのときu_x=0\text{[mm]}、\theta=11.25^\circ, 22.5^\circ, 33.75^\circのとき、横変位が発生し、計算通り\theta=22.5^\circの時、最大の値u_x=3.74\text{[mm]}となりました。ここから圧縮力がせん断変形に変換されるメカニカルメタマテリアルを設計できたことがわかりました。
FDM3Dプリンタを用いた試作
試作
最後に実試作による実験をして、設計通りの挙動をするか確認してみましょう。
試験片はFDM(熱溶解積層方式)3Dプリンタを用いて造形します。
材料は大きく変形させたいので軟質材料のTPUを用います。
圧縮試験は荷重変位試験機を用いて行います。
結果

結果は上図のようになりました。
シミュレーション通り\theta=22.5^\circの時に最も大きくせん断変形しました。
\theta=0^\circ, 11.25^\circ, 22.5^\circでは安定した変形を起こしていますが、
\theta=33.75^\circ, 45^\circでは圧縮力により座屈が起こってしまっています。
圧縮試験動画


圧縮試験の動画でみると回転の有無でせん断変形が誘導されていることがよくわかります。
せん断変形時に上面が大きくスライドし、推進力を生みだしそうな変形となっていますね。
まとめ
圧縮力をせん断変形に変換するためには、ヤング率とせん断率の比が大きい特殊な材料を回転させれば良いことを材料力学の観点から明らかにしました。2つのラティス構造(Xラティス・+ラティス)について、均質化法を用いて等価なマクロ材料物性を計測し、上記性質を持つことを確認しました。また、Xラティスと+ラティスは回転させると一致することを幾何学的観点と材料力学的観点から理解しました。最後にシミュレーションと試作実験により、圧縮力がせん断変形に変換されるメカニカルメタマテリアルが設計できたことを確認しました。
次回は回転させたXラティスを用いて踏み込み力を推進力に変換するミッドソールを設計していきたいと思います。
参考文献
[1] 寺田 賢二郎, 均質化法を用いた複合材料の解析, 成形加工, 2017, 29 巻, 2 号, p. 42-46, 公開日 2020/09/10, Online ISSN 1883-7417, Print ISSN 0915-4027
[2] 寺田 賢二郎,平山 紀夫,山本 晃司,数値材料試験 有限要素法によるマルチスケール解析,丸善出版,2021,ISBN 978-4-621-30633-8