発想 idea
弊社は、日々「カタチ」について探求をしている会社です。すでに世の中にあるカタチを理解しながら、まだ世にないカタチをどうやって生み出すかについても研究を続けています。そんな新たな形を創造する方法として、計算機を用いた形状生成について調査している過程で、marching cubesという手法に出会いました。
marching cubes[1]は、1987年にLorensenとClineによって発表されたコンピュータグラフィックスアルゴリズムであり、3次元の離散スカラー場から等値面の多角形メッシュを抽出します。このアルゴリズムは、主にCTやMRIスキャンデータ画像などの医療用ビジュアライゼーションに用いられます。
また、marching cubesは、3Dに使用することを意図して作られたアルゴリズムですが、このアルゴリズムを2Dに適用することも可能であり、その場合はmarching squaresと呼ばれています。
marching squaresの代表的な使用例は、天気図での等圧線の描画や地図上の等高線の描画です。地図上で格子状にマッピングされた離散的な情報をもとに、大気圧の滑らかな変化を推測し、地図に重ねて表示します。marching squaresは計算が軽量であることから、時々刻々変化する気圧の測定値を瞬時に変換し、観測する人間にとって感覚的に理解しやすい画像を届けることが可能となっています。
marching squaresはすでに幅広く利用されている技術ですが、今回はあえてこのmarching squaresをRhinocerossのGrasshopper上で1から処理を実装することでアルゴリズムを理解しながら、色々な画像を処理、生成して遊んでみたいと思います。
調査 research
まずは、marching squares法のアルゴリズムの理解から始めます。
Wikipedia[2]に大変分かりやすい説明があったので、補足を加えながら引用させていただきます。
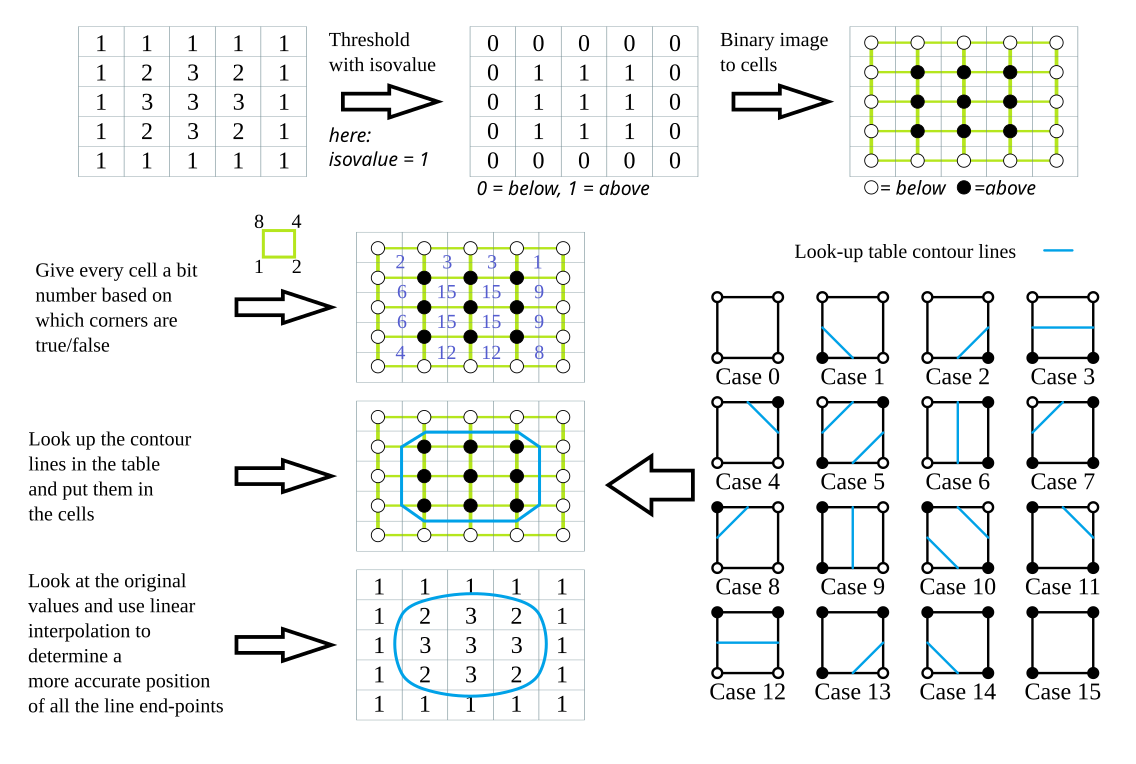
アルゴリズムの手順
①データの二値化
2Dスカラー場の値を、基準値(しきい値)を使用して二値化し、白黒のピクセル画像にします。
- 基準値以上の場合は「1」とする。
- 基準値未満の場合は「0」とする。
②輪郭セルの作成
二値化された画像の2x2のブロックに対して、1つの「輪郭セル」を構成します。この輪郭セルのグリッドは、元の2Dスカラー場に比べて各方向に1セル小さくなります。(下の図では、もともと5*5の離散スカラー場を持っていましたが、この処理により4*4のグリッドに変わります。)【ここから各セルごとの処理します】
③セルインデックスの決定
輪郭セルの4つの角(バイナリ値1または0を保持)を時計回りに巡りながらセルインデックスを作成します。このインデックスは4ビットの値となり、0から15までの16通りの状態のどれかを表します。④ルックアップテーブルの参照
生成されたインデックスを使用して、事前に用意されたルックアップテーブルを参照します。ルックアップテーブルには、セル内のどの辺に輪郭線が通るべきかが指定されています。marching squareで使用するのは、このルックアップテーブルに記載された基本16種の形状だけです。⑤線形補間
セルの辺上で、元の2Dスカラー場の値を使用して、輪郭線の正確な位置を線形補間によって補正します。これにより、先ほどの基本16種を変形しより滑らかな境界線を得ることができます。
①②を実行後、③~⑤をセルごとに順々に処理することで等値線を表す境界線が描かれていきます。
16種の形状パターンを4bitのバイナリに対応させて処理する過程が、萌えポイントですね。
構築 build
marching squares法のアルゴリズムの手順で確認した、16種の基本形状を用いて境界線を表現する④の状態と、線形補間を適用した⑤の状態には少し開きがあるので、marching squaresの実行段階を以下の3つの状態に分けて考えます。
| state | name | description |
|---|---|---|
| 1 | marching squares threshold | しきい値によって2値化した状態。ドット絵の状態。 |
| 2 | marching squares 16 pattern | セルインデックスに対応した16種の基本形状を割り当てた状態。グリッドに対して45度の境界線を持つことができ、表現力が向上。 |
| 3 | marching squares linear interpolation | しきい値に分解する前のスカラー場の値を使って線形補間を適用した状態。滑らかな境界線を表現可能。 |
16種の基本形状
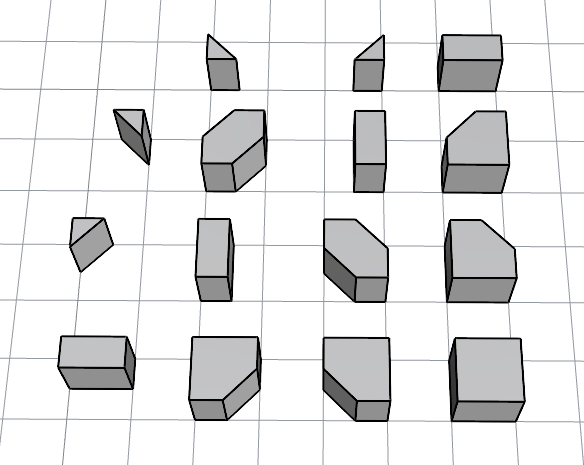
16種の基本形状をrhino上で、立体のソリッドポリサーフェスとしてモデリングしました。2Dの画像処理を想定しているので、高さは仮置きで1として統一しています。下の図を見ると15種しかないように見えますが、「左上の何もない空間」も形状を表す状態の1つとしてカウントしているので、全16種になります。
state 2の処理では、この16個のブロックを積み木のように配置していくことで、形状を再現します。
バイナリ演算
grasshopper上でのバイナリ演算は、Python Scriptコンポーネントの中で、pythonコードとして処理しました。セルの周囲4点のノードのバイナリ値(0か1)を並べて、4bitの数値として読み取り、それを10進数の0~15の数字として出力します。この0~15の数字に対応したブロックを、先ほどの形状群から選択し、そのセルの位置に配置すればmarching squaresを適用した形状が作られていきます。

Python 3 Script
# n: 正方形ピクセル画像の縦横ピクセル数
# p: 各ノードの値(0or1)(ex n=64のときpは1024個のリストデータ)
def convert_to_matrix(n, p):
matrix = []
for i in range(n):
row = p[i*n:(i+1)*n]
matrix.append(row)
return matrix
def calculate_p_values_as_int(n, p):
# 一次元リストを二次元行列に変換
p_matrix = convert_to_matrix(n, p)
results = []
for i in range(n-1):
for j in range(n-1):
# 4ビットのバイナリ数値を文字列として取得
binary_str = f"{p_matrix[i][j]}{p_matrix[i][j+1]}{p_matrix[i+1][j+1]}{p_matrix[i+1][j]}"
# バイナリ文字列を整数に変換
int_value = int(binary_str, 2)
results.append(int_value)
return results
#各輪郭セルのバイナリ値(0~15)
results = calculate_p_values_as_int(n, p)
print(results)線形補間
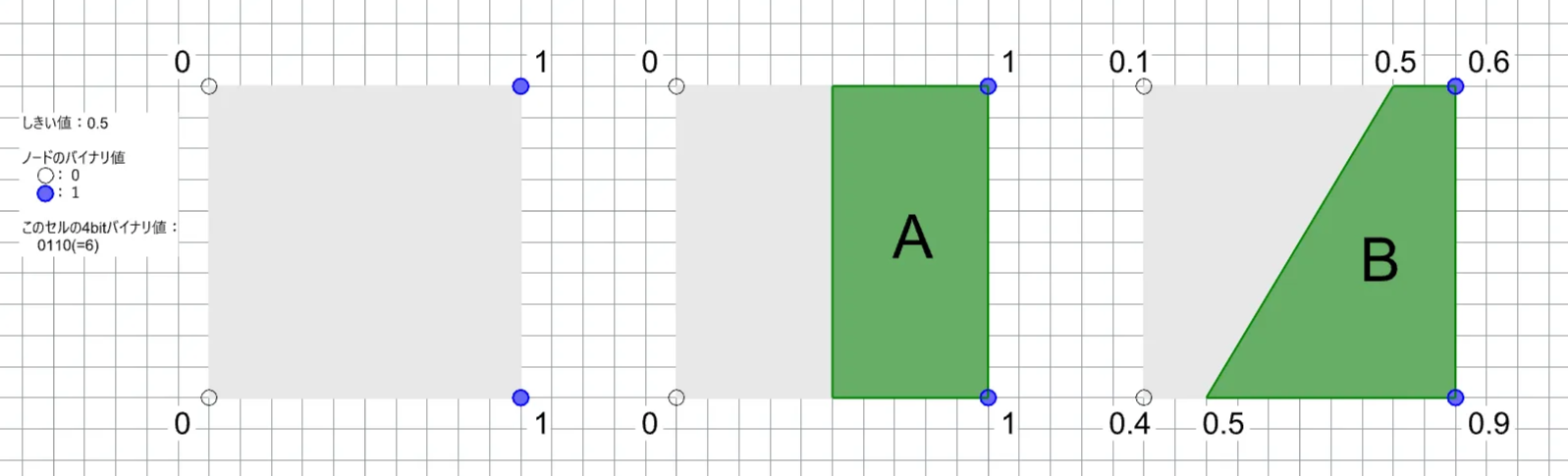
アルゴリズムの⑤にある線形補間を施すことで出力される画像をより滑らかにすることができます。線形補間の例として、あるセル(4bitバイナリ値「0110」)に対する処理を下図に表しました。
まず、一番左の図形は、スカラー場に対して、各ノードの値をしきい値0.5によって、01のバイナリ値に変換した状態です。このセルについて、左上から時計回りにノードのバイナリ値を読み取ると「0110」となっています。「0110」は10進数で読み取ると「6」のブロックに対応しているため、そのブロックを配置します。画像中央のAの形状がそれを表しており、アルゴリズムの実行段階としては、state 2になります。
このAの形状を得た後に、0と1の中間にある角について、しきい値で分類する前のスカラー値(ここでは、0.1, 0.6, 0.9, 0.4)を用いて、線形補間によりしきい値(0.5)の座標を推測し、形状を変形させる操作を行います。これによって、得られたBの形状が、アルゴリズムの実行段階としては、state 3になります。
実行 test
上記で構築した要素を組み合わせて、Marching squares法の実行環境をGrasshopper上に作成しました。
以下にそれを使用した実施例として、①ピクセル画像の境界を滑らかに変換した例と、②ランダム生成したスカラー場の等高線可視化した例を紹介します。
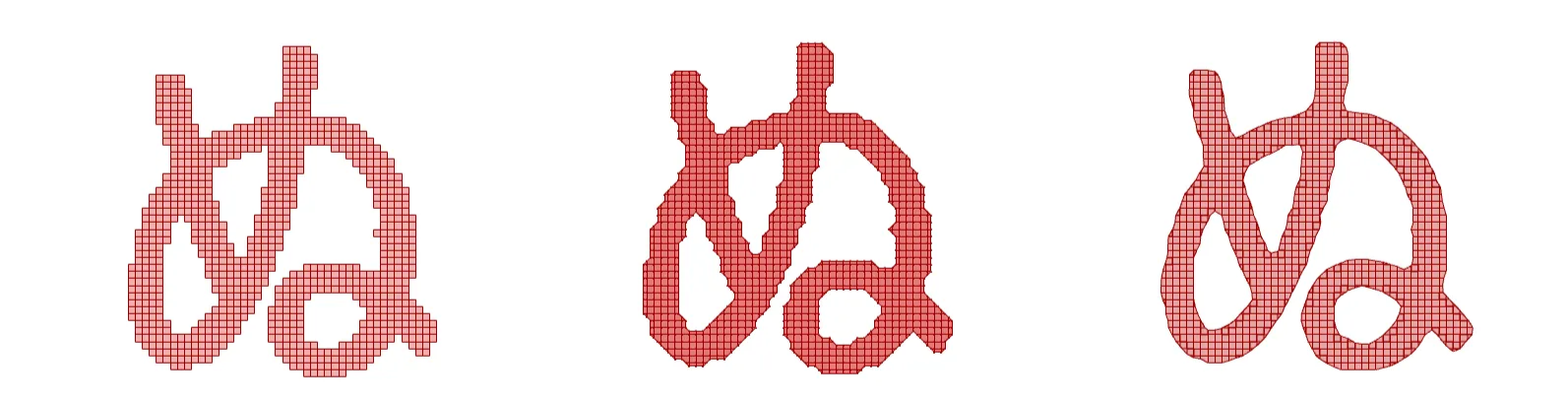
① ピクセル画像の境界を滑らかに変換
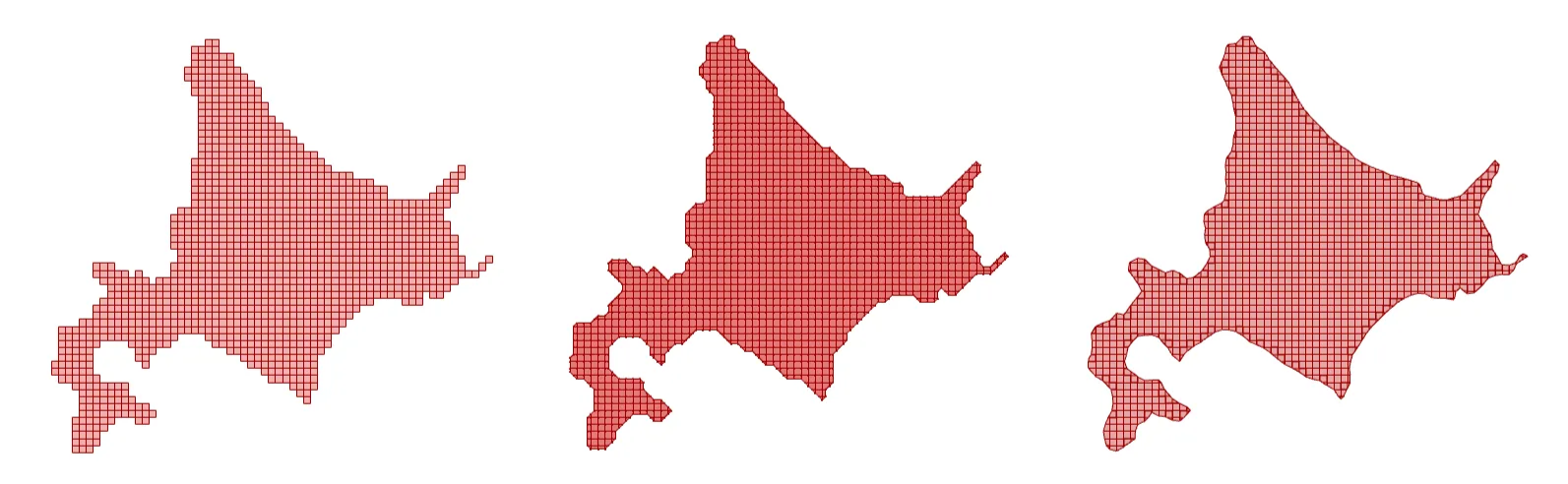
ここでは、様々な64×64のピクセル画像に対して、marching squaresを適用した過程を、3つの実行段階ごとに示します。左からstate1, state2, state3の順で並べてあります。
どの画像も右に行くほど境界滑らかで、綺麗な画像に見えると思います。一番左のドット絵では、1つのセルサイズよりも細い形状は表現しきれませんが、一番右の画像では細い部分もちゃんと表現できています(北海道の根室半島がきれいに表現できています)。また、車の丸いタイヤ形状やペンギンなどの曲線形状では、ピクセル表現では不自然に感じる場合がありますが、marching squaresを適用することで自然な滑らかさを感じることができるようになります。


グレースケール画像との比較
上記の画像処理では、state 2からstate 3に変換する際に、元画像の情報として、各ノードに与えられた0~1の間の数値を持ったスカラー値を使用しています。このスカラー値を光度に対応させて描画したグレースケール画像と、そこからmarching squaresを適用して境界を抽出した結果を比較してみましょう。
下図は、ペンギンのひれの部分の拡大図です。左側のグレースケール画像の場合は、ピクセルの直角な境界が目立ち、自然なひれの形状には見えません。一方で、右側に重ねたのmarching squaresによる画像は、同じ情報量でありながら、滑らかな形状が人の目でも観測しやすくなっています。

② ランダム生成したスカラー場の等高線可視化
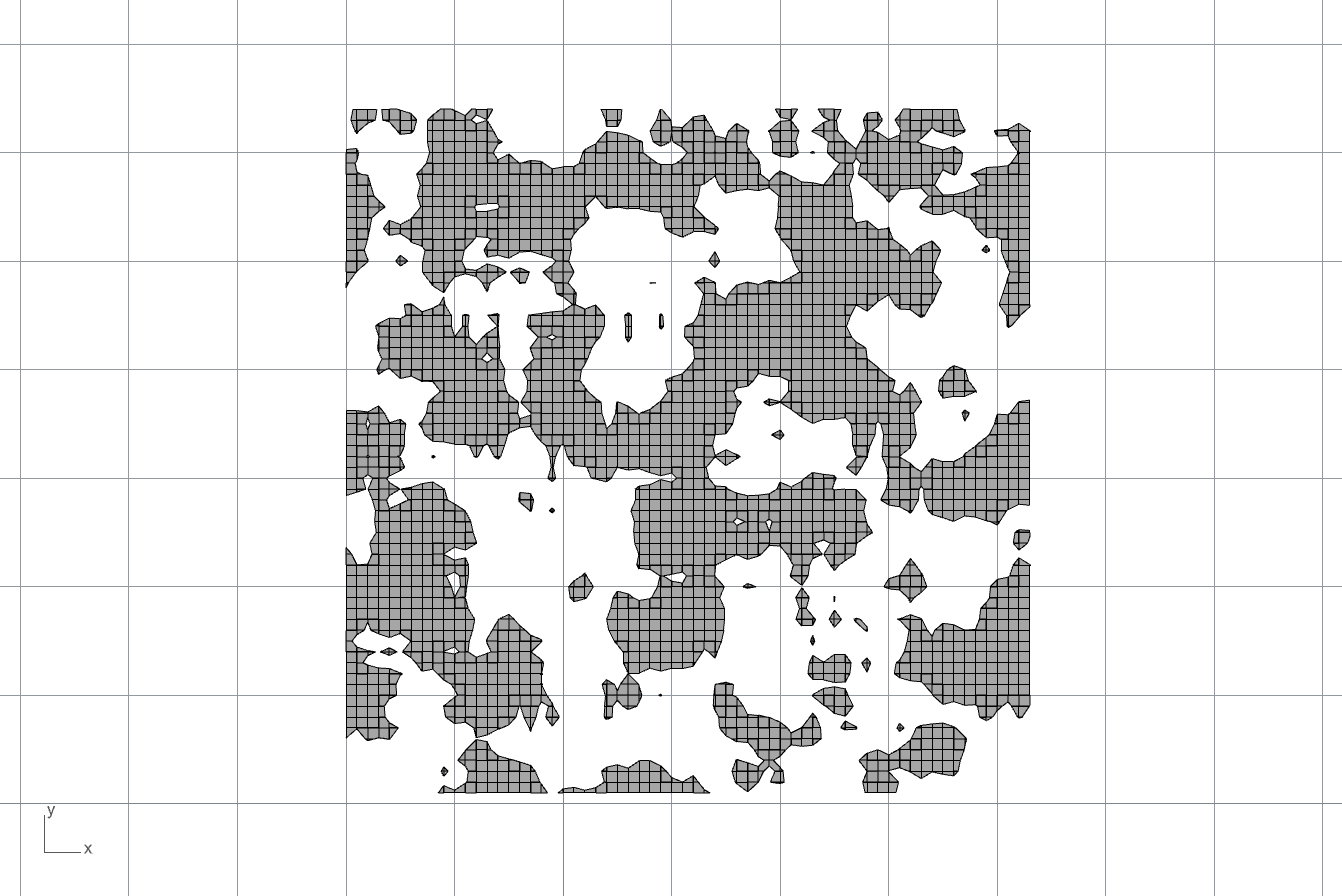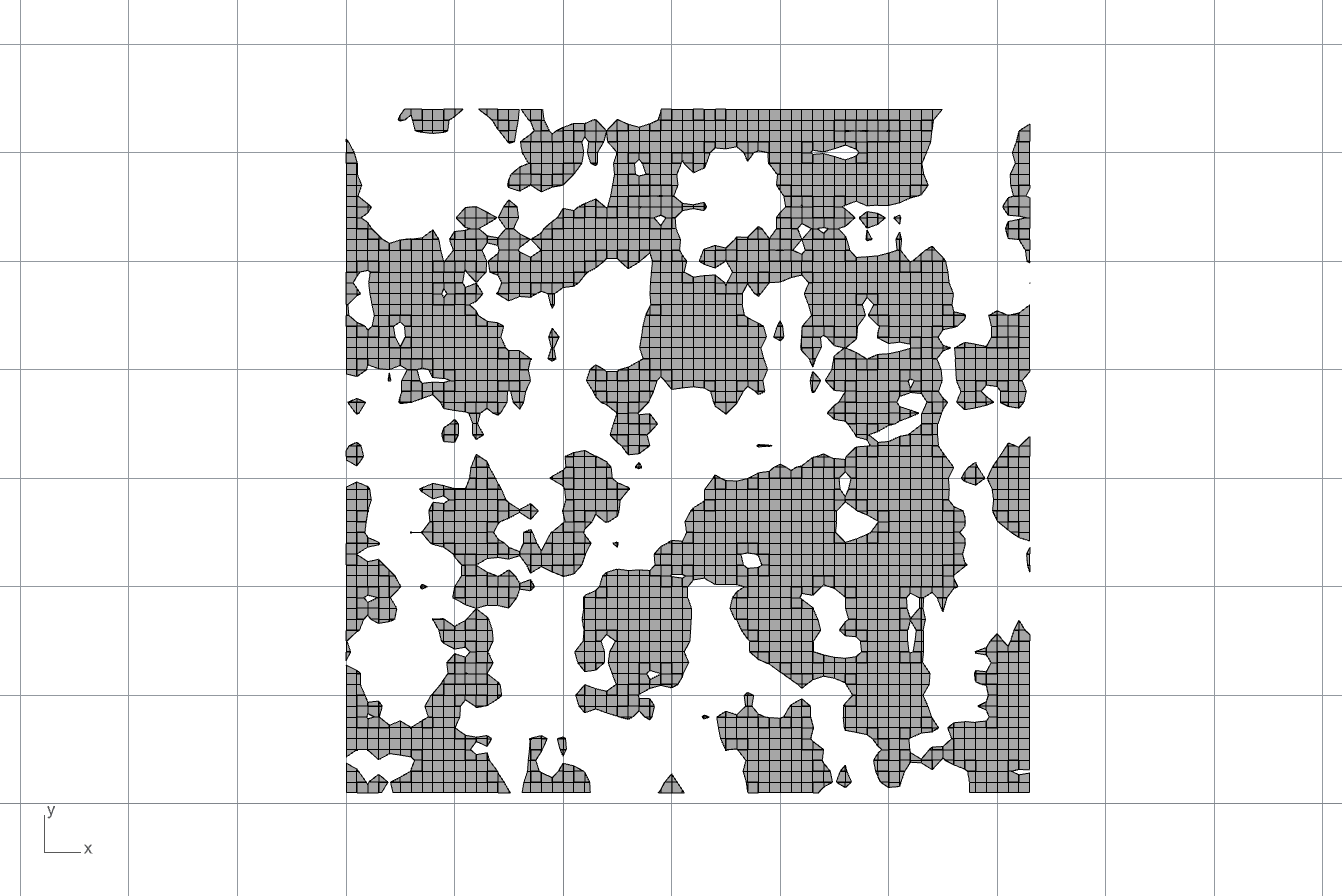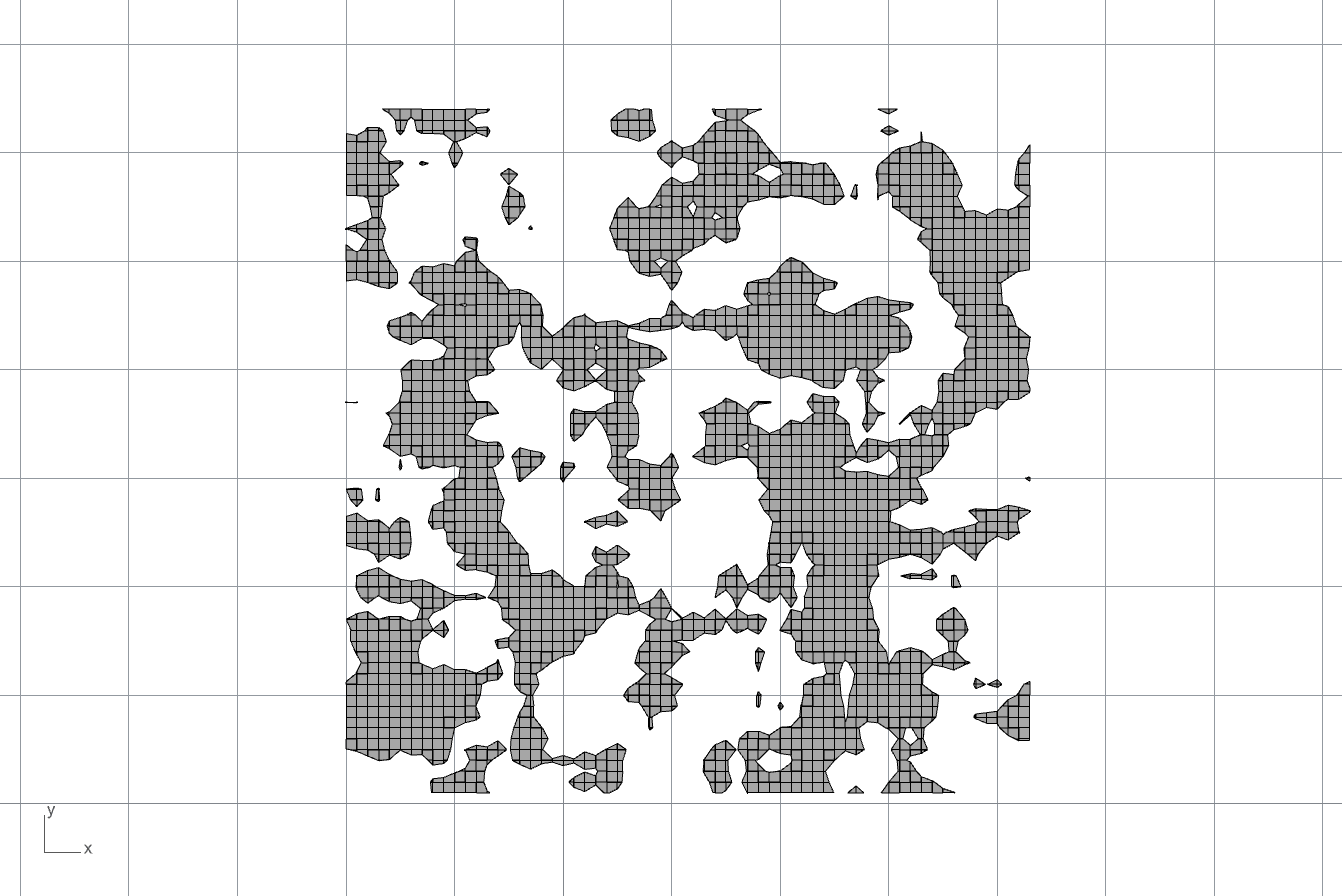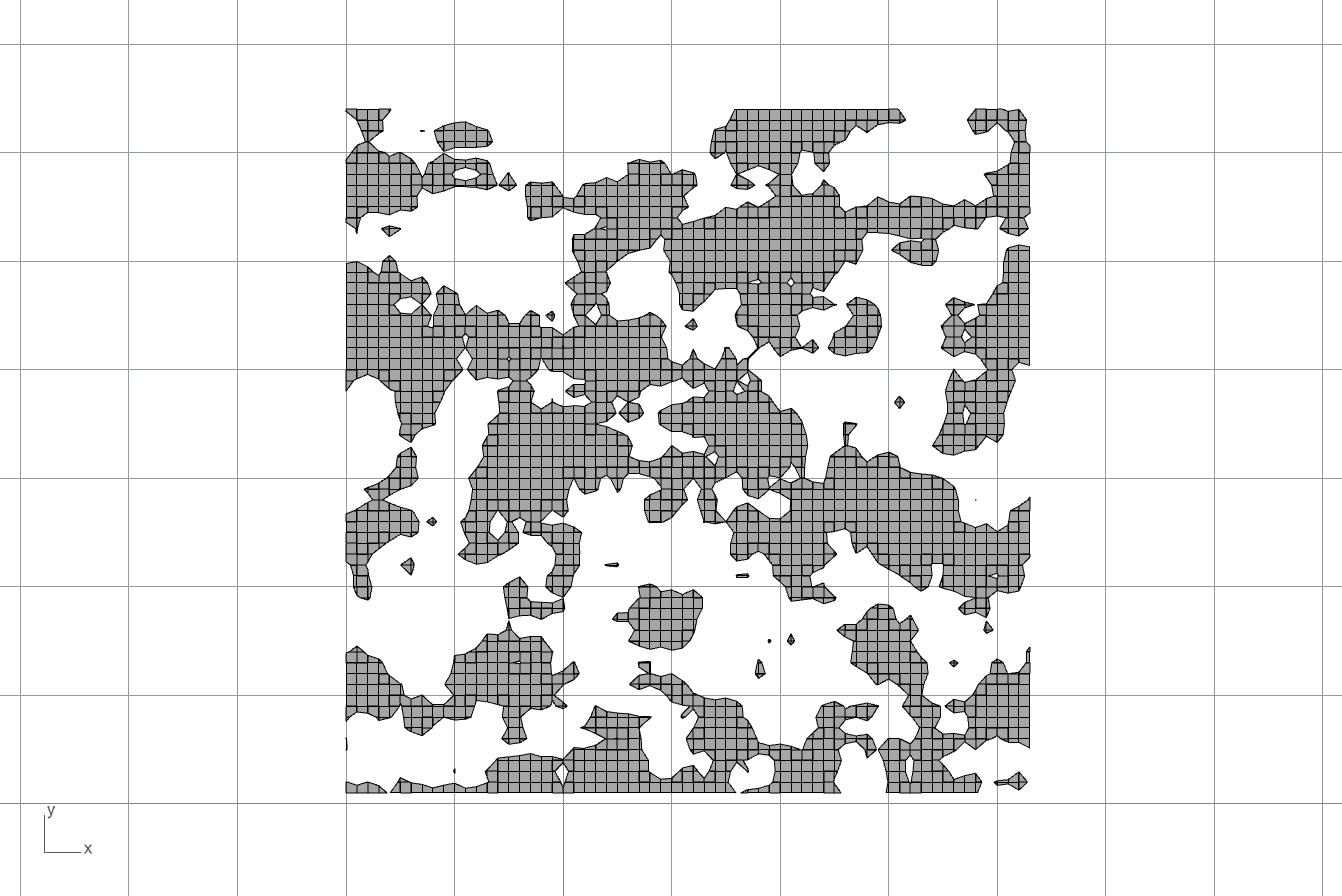
続いて、64×64のグリッドにランダムな数値を与えてスカラー場を構築し、そのスカラー場に対してmarching squaresを実行した例を示します。スカラー場には、平均化のフィルタをかけており、フィルタを徐々に強くしていくことでランダム値の変化を平坦にしていった様子をgifにしてみました。
もっとも細かい模様から始まって、徐々に大きな塊の模様に変化していきます。この画像自体に物理的な意味はありませんが、スカラー場に意味を持たせれば有用な形状を生成することも期待できます。

つぎに、一定の平均化フィルタを用いて、元のランダム値のシード値を振った場合の画像をgif化してみました。こうすると、同程度の形状粒度を持った、様々な画像が得られます。
私には存在しない大陸をかたどった無数の地図を生成しているように見えますが、皆さんは何を創造するでしょうか。
おまけ extra
冒頭でmarching squaresは、marching cubesの2Dバージョンであるという説明をさせていただきました。ここでは少しだけ、marching cubesにトライした結果をまとめておきます。
marching cubesでは、marching squaresの1つのセルが、立方格子に拡張され8つの頂点を持ちます。この点の0, 1によって表現される基本形状は、下図の30個の図形をXYZ軸に回転させて重複を除いた256個の形状です。これは、8つの頂点のバイナリ値によって作られる8bitのバイナリ値が表現できる0~255の全256通りに等しい数になります。
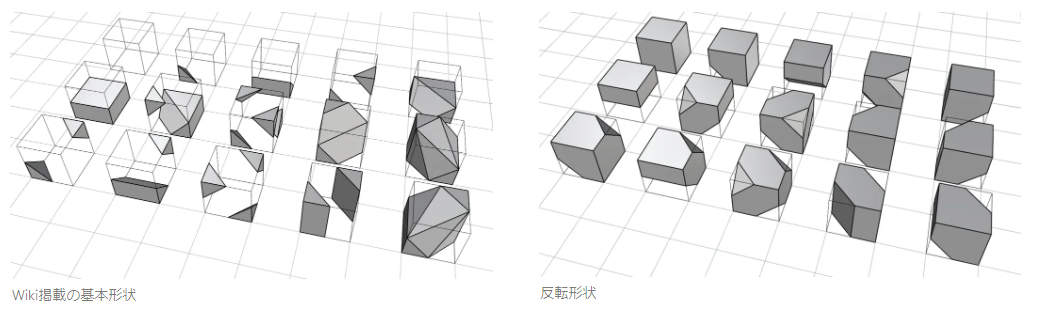
下にいくつかの形状について、表現したい正解データと、立方体のみで表現したボクセル表現と、maching cubesのstate2に相当する256個の基本形状ブロックで表現した状態を並べてみました。
3次元形状になると256通りのブロックを用いても、なかなか滑らかと言える表現力を持たせることができませんでした。3次現空間においても、2次元と同じく線形補間が可能ですが、grasshopperでの実装はそれなりに複雑になりそうなので、今回は取り組みではstete 2までとしましたが、marching cubesの効果の片鱗は感じられたかと思います。




振り返り review
今回は、marching squares法を用いて、ピクセル画像から滑らかな境界線を作成したり、ランダムに生成したスカラー場から新たな境界線を作成したりしてみました。marching squaresの手法自体は、グレースケール画像を加工して境界を見やすくしているだけとも言えますが、出力された滑らかな形状を人が見ることで、その感じ方、印象は大きく変わるため、そこから得られる情報、発想に差が出てくるかと思います。
使用したソフト
[1] Rhino 8, Grasshopper
参考文献、サイト
[1] https://dl.acm.org/doi/10.1145/37402.37422
[2] https://en.wikipedia.org/wiki/Marching_squares
[3] https://www.youtube.com/watch?v=0ZONMNUKTfU&ab_channel=TheCodingTrain
[4] https://jamie-wong.com/2016/07/06/metaballs-and-webgl/
[5] https://ragingnexus.com/creative-code-lab/experiments/algorithms-marching-squares/
[6] https://www.3dbenchy.com/

