はじめに

おはようございます。突然ですがみなさんは流体を回していますか？

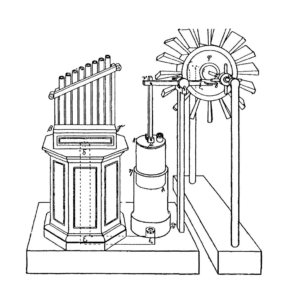
人類が流体（水だったり、空気だったり）を回したり、逆に流体からモノを回転させる力という形で力を取り出して利用し始めたのはいつからだったのでしょうか？明確な起源は不明ですが、既に紀元一世紀古代ローマにおいてアレクサンドリアのヘロンが風力によって機械（オルガン）に動力を供給する、風車に類する装置を開発していたことが記録に残されています[1]。

人類にとって非常に古い付き合いになる流体動力⇔機械動力の変換ですが、現在でもその恩恵に我々は多く預かっています。例えば、日常シーンでは電力確保(風力発電はもちろん、各種火力発電も結局のところ流体でタービンを回して電力を得ています)、水道水の給水、換気等様々なところで活用されており、これ無しでは現代人の生活は成り立たないと言っても過言ではありません。

このように様々なところで使われていることから、その効用や効率を知ることは工業的にも非常に重要です。しかしながら、CFD流体解析技術者の方に回転する物体に対する解析を行ってくれ、と言うと、おそらく微妙に嫌そうな顔をされる事が多いのではないでしょうか。

CFDは大雑把には、流体が通る解析空間を微小な空間に分割（メッシュ作成）し、その上でナビエ–ストークス方程式を解くことによって解析を実行しています。一方で回転する物体の周りの流体空間を考えると、ある時間とそこから一定時間経った後の解析空間を比較すると、物体によって流体が排除されている空間が異なる=解析空間が変化してしまっている、と捉えることが出来ます。よってある時間のメッシュ≠一定時間後のメッシュであり、解析する為には毎回メッシュの再作成が必要となります。時間方向の刻み方にもよりますが、基本的には莫大な計算リソースが要求されることになるでしょう。

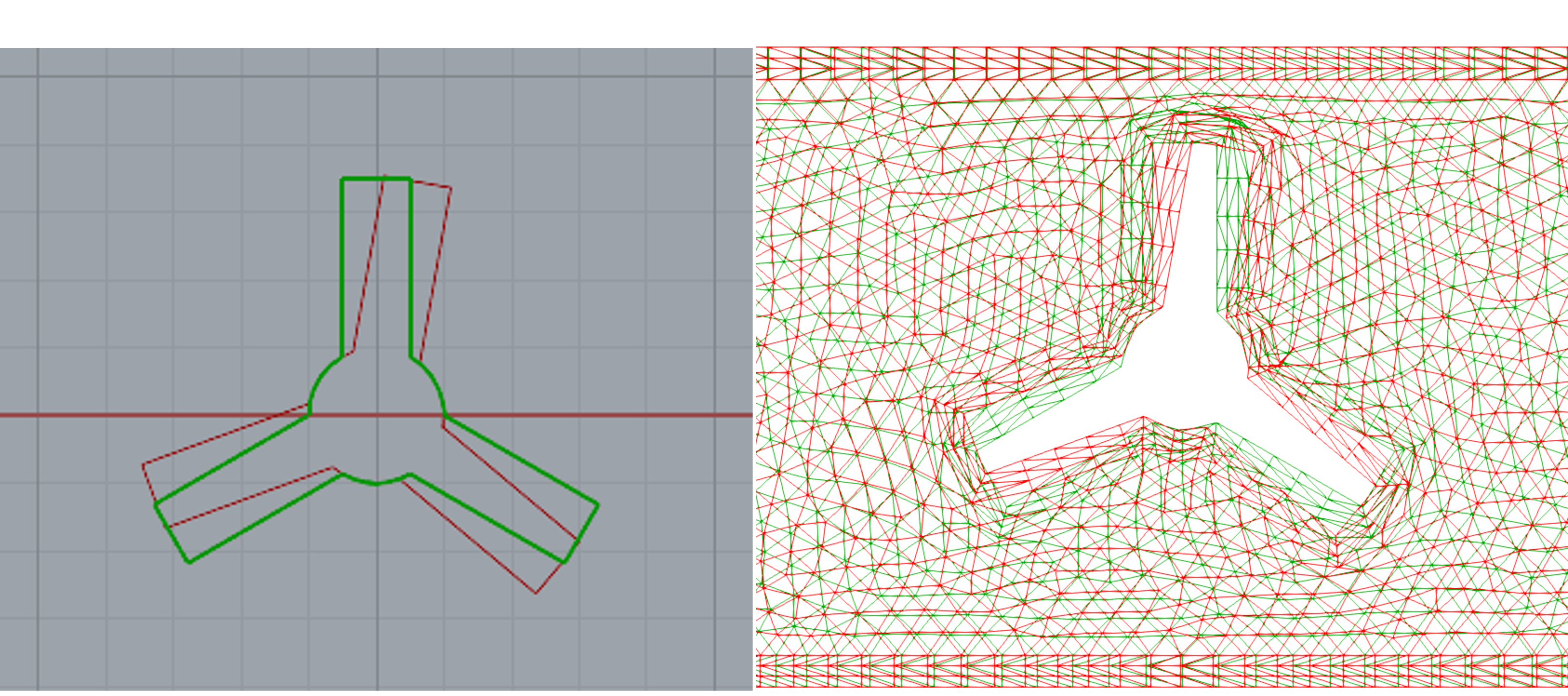
以上に示すように、CFDの仕組みが回転体とそもそも相性が良くないことが分かります。しかしながら、この用途の解析需要は高いことから、様々な手段/手法で問題を解決できるよう研究者/技術者達は取り組んできました。本記事ではその文脈に則って大まかにどのようなことを考えながらこの課題に取り組んでいるかを書きます。

形状を再現せず、回さない

以前の拙作記事でも述べました通り、解析技術者として一番重要なことは「解析しないで済むものは解析しない」ことになります。よって、そもそも本当に回転することを再現する必要があるのか？と言った観点からまず考えるといいでしょう。

一例として液体をくみ上げる機構（送風機やポンプ等）を考えてみましょう。

液体をくみ上げる機構は通過した流体の圧力を上昇させ、流体が圧力が高いところから低いところへ流れることで移動を発生させています。つまり、「機構によって上昇させられる圧力>それ以外の部分における流路の圧力損失」が成立すれば流体の流れは発生する、と考えることが出来ます。そこで解析上良く行われる手段として、この機構部分の形状はCFDで再現せず、「機構から送られてきた流れ」自体を入口境界条件としてしまうことがあります。

手前味噌ですみませんが、一例として、弊社Tech Blog記事の解析事例を例に考えてみます。

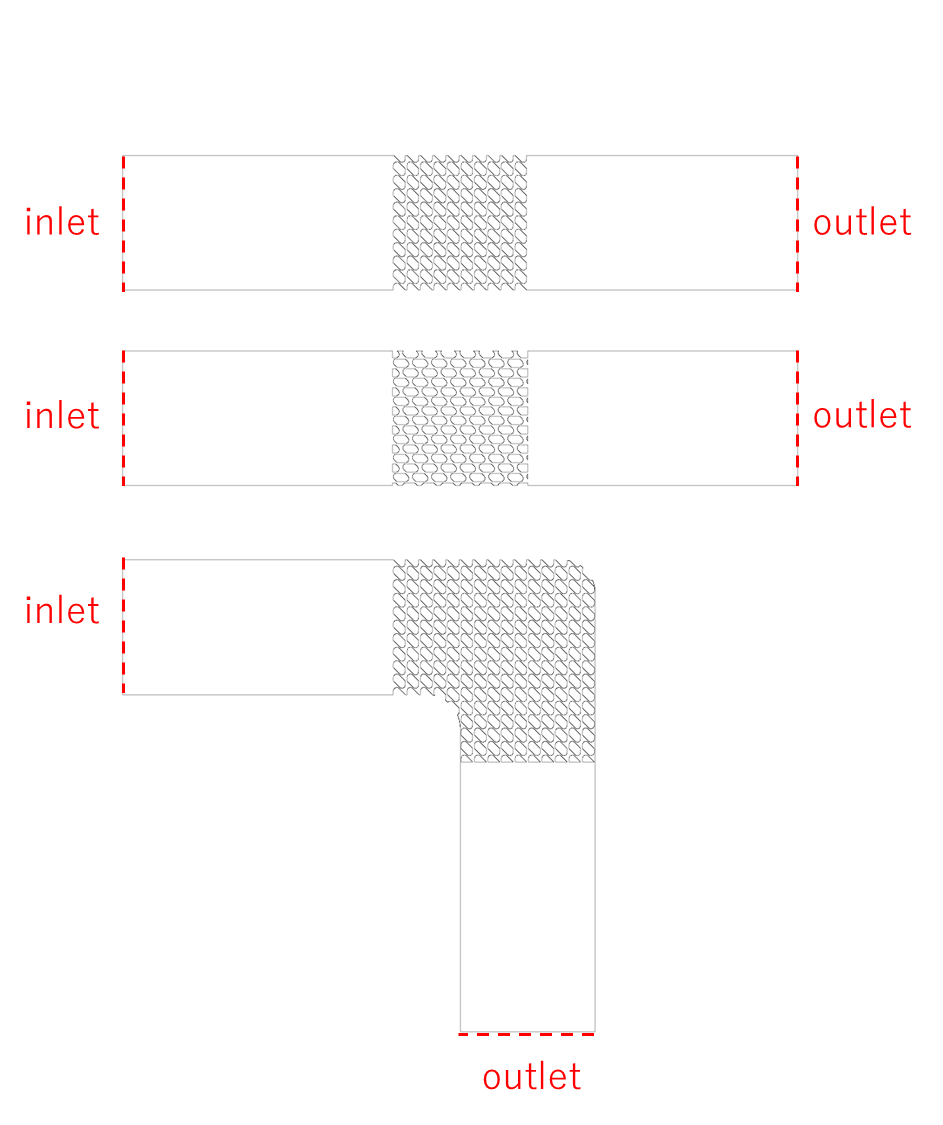
記事内で明示的には書かれていませんが、この系を実際に作って流体を流す実験を行うことを考えると、送風機によって昇圧し、流体を流し込んで性能を検証することになるでしょう。その昇圧分を入口の境界条件として与えることで代替している、と読み替えることが出来ます。

こうすることで、送風機内部の複雑な形状と回転を再現せずとも比較的簡単に解析を行うことが出来ます。これは電気回路に組み込まれた電池を考える時、電池内で起きている化学反応の詳細まで考えず、ただの「+1.5V」と見なすことに近いでしょう。 ここで視点を代えて一般に販売されている既製品を見てみると、水流ポンプであれば推奨の揚程と吐出し量(=上昇させられる圧力と流量に相当)が、換気ファンであれば風量-静圧特性曲線がカタログスペックとして公開されていたりします。このことからも、上記のような使用方法がある意味では標準的に想定されていることが伺えます。

また別例として風車による発電装置について考えてみます。一般に風車は年間の風量が一定以上見込める（有り体に言えば”稼げる”）ところに、総発電量を増やすことを目的とし複数本集中的に建てることが多く行われております。一方で、風車に運動力を一度与えてしまった風の持つエネルギーは減衰する為、その風下の風車を回す力は弱くなってしまうことが知られています。一般にこの現象はウェイクと呼ばれています。風車は大型施設故、なるべく実際に建てる前からその性能を予測する必要性があり、流体解析が多く用いられることになります。

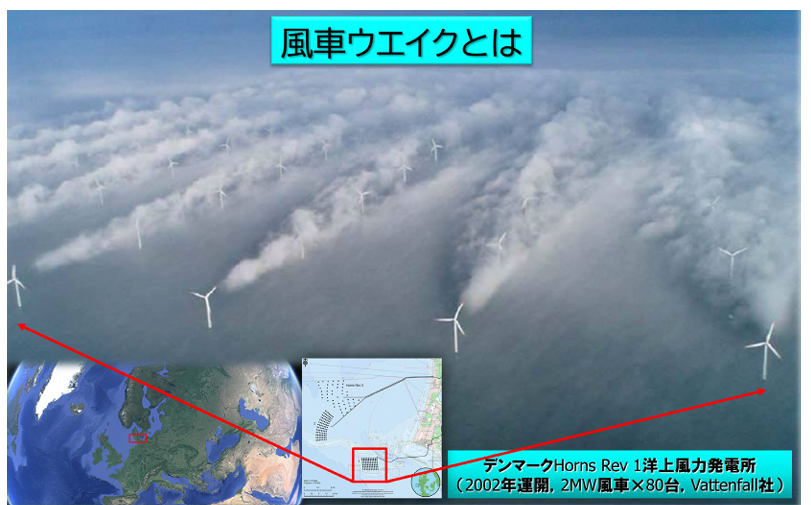
このような状況を再現する解析を行うとき、現象をマクロ的な視点で見て、風車後流の風の勢いが衰えること、即ち「羽根の存在しうる領域を通過した風に対して変化を与える」という様相に着目しある種の簡略化したモデルを埋め込むことで計算を行う、といった取り組みがなされています。

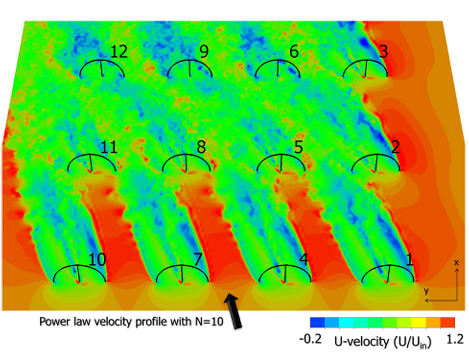
以上のように、回転体直前直後の詳細な流れの様相や、そもそもの性能が知りたいとき等を例外とし、マクロ的な視点で回転機械を見ている時は基本的には数値解析で回転する現象そのものを再現する必要はないと言えるでしょう。

形状は再現するけど、回さない

さてどうしても近傍の流れ方を知りたい場合は諦めて回転体形状のメッシュを切りましょう。でもあくまで簡単の為の抵抗を試みます。

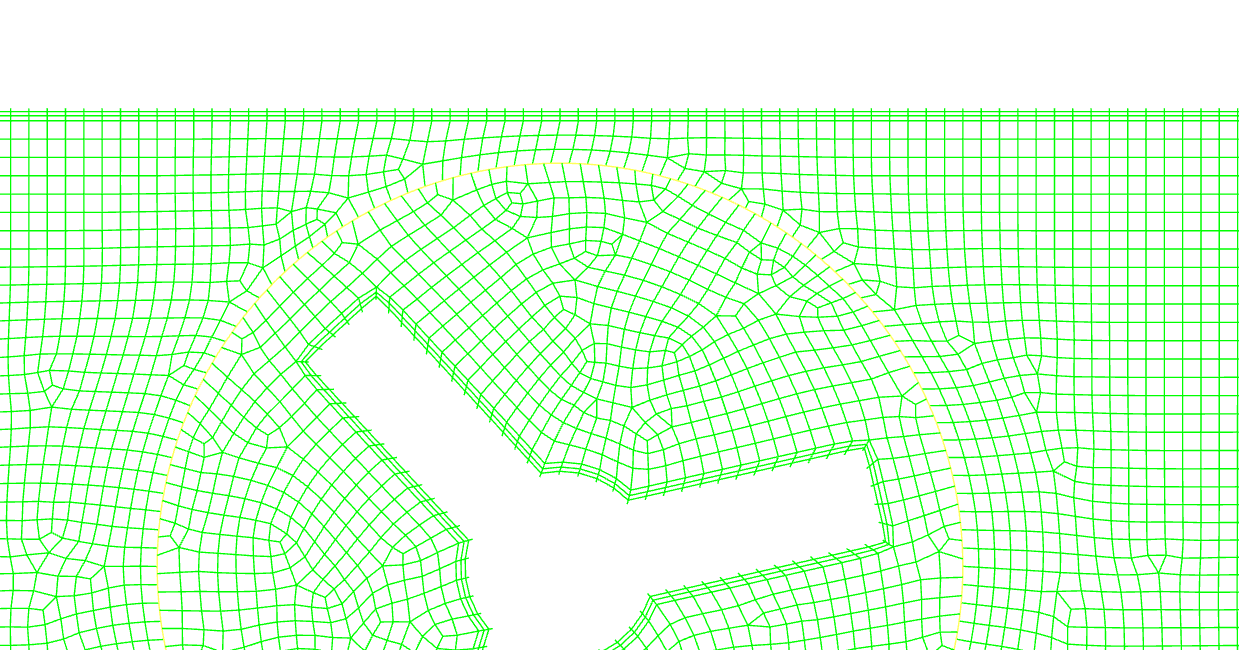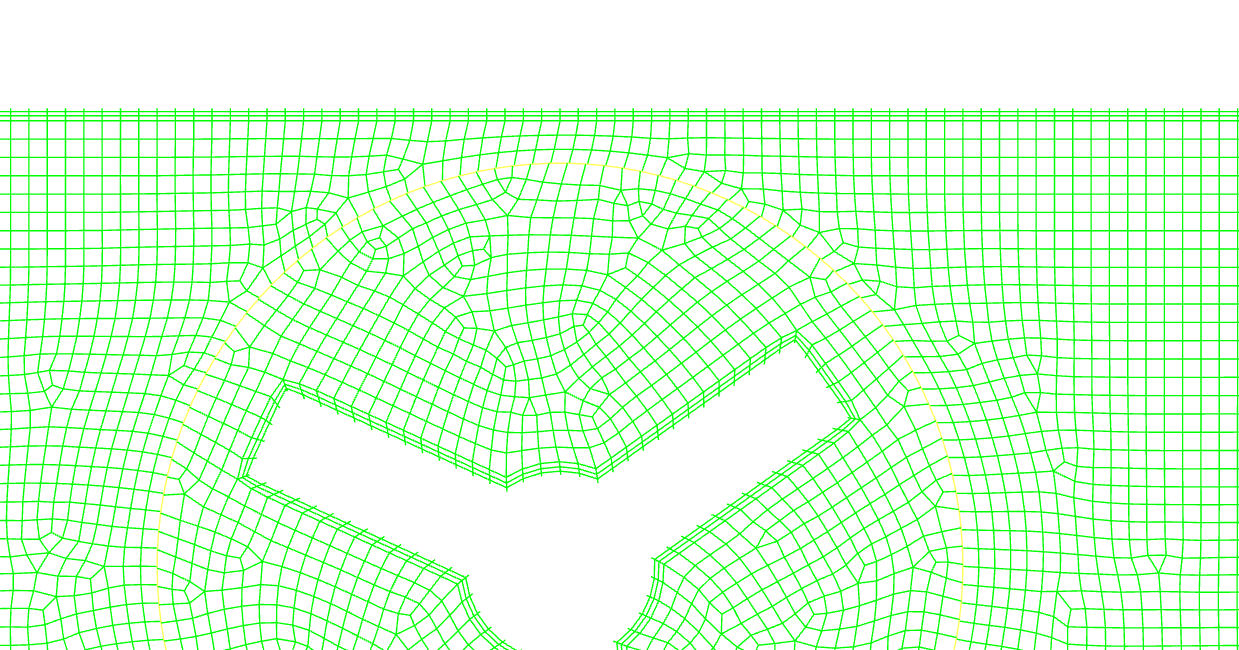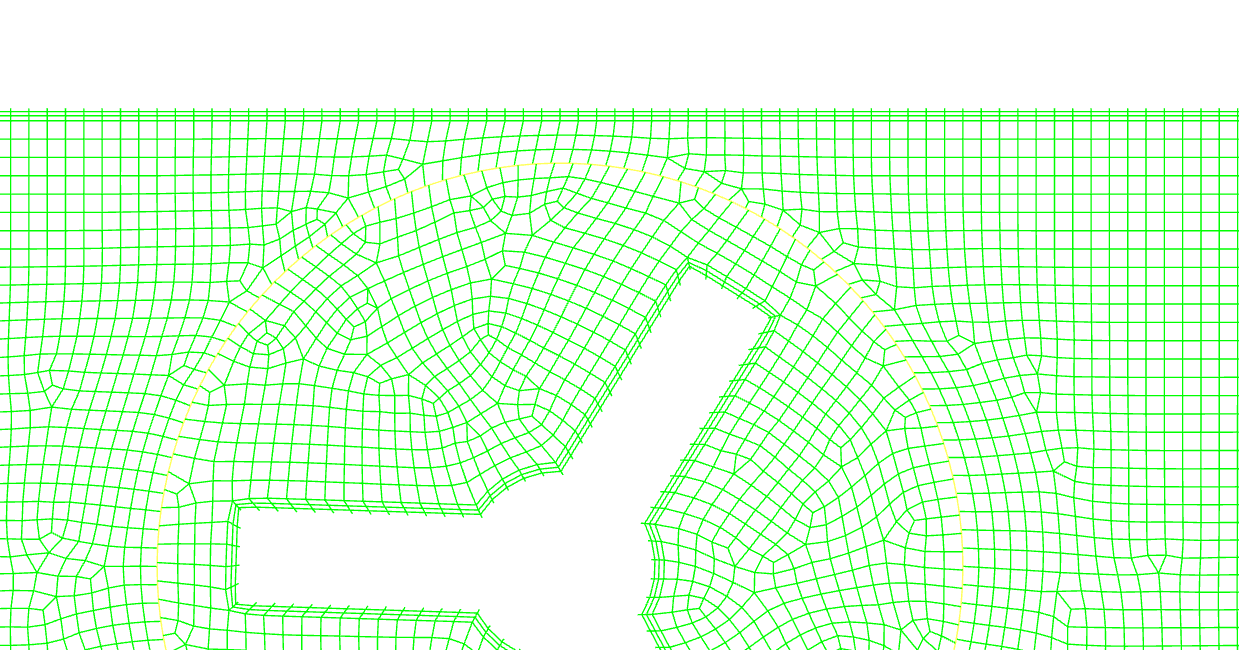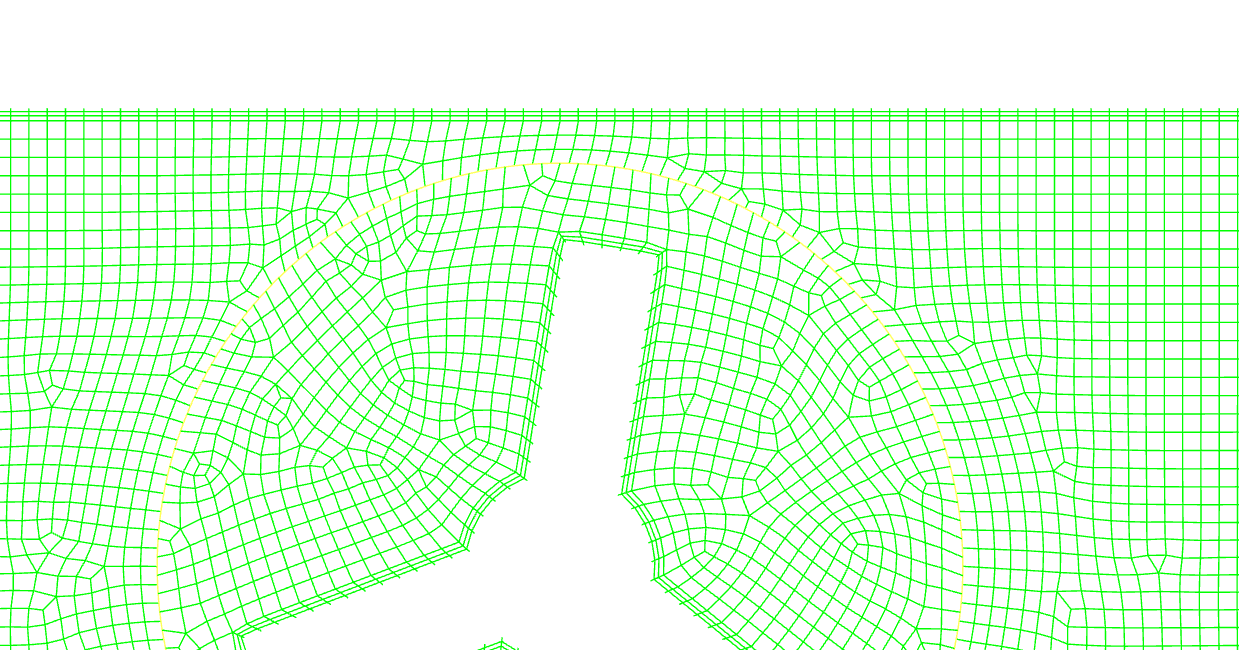
回転する要素とその以外の構造の相互作用がそれほど強くないと想定される状況であれば、MRF(Multiple Reference Frame)と呼ばれる手法が適用できます。これは、領域を回転する要素と回転しない要素に分割し、回転する要素のある領域を回転している座標系、回転しない領域を静止座標系上で解析する手法になります。これを行うことによって、見かけ上は静止状態のまま、静止座標上では流体が回転の影響を受けている様子を観察することが出来るようになります。

上図は円周内のセルを回転座標系に設定したMRFの周囲の二次元流れをベクトルで表示したものになります。静止座標上で静止している壁は回転座標上では回転しているように振る舞って影響範囲の気流を回している様子が見られます。また、上下で反対方向に回していますが、それに合わせて全体的な流れの様相が逆になることも観測できます。 あくまでこれは実現象の近似になりますが、多くの場面で妥当な流れを再現できることが知られており、実用面的には性能/コストバランスの優れた本手法が多く用いられる傾向にあります。

諦めて回しましょう

MRFは多く用いられていますが、対称性の低い形状の回転による影響の再現や、回転することによって齎される周期的に変調される流速に起因する現象、例えば音等の正確な表現は難しいとされています。 ここまで来て万策尽きたら諦めて回しましょう。ただし、先に述べたように毎イタレーションメッシュ切り直し等非現実的な解析時間がかからないよう、この状況下においても様々な策が弄されています。

ここでは代表的な例としてスライディングメッシュを取り上げます。これは回転体周囲の領域とそれ以外の領域とで別々にメッシュを作成し、その名の示す通り回転領域がスライドしながらズレていくことで回転する様子を再現する手法になります。

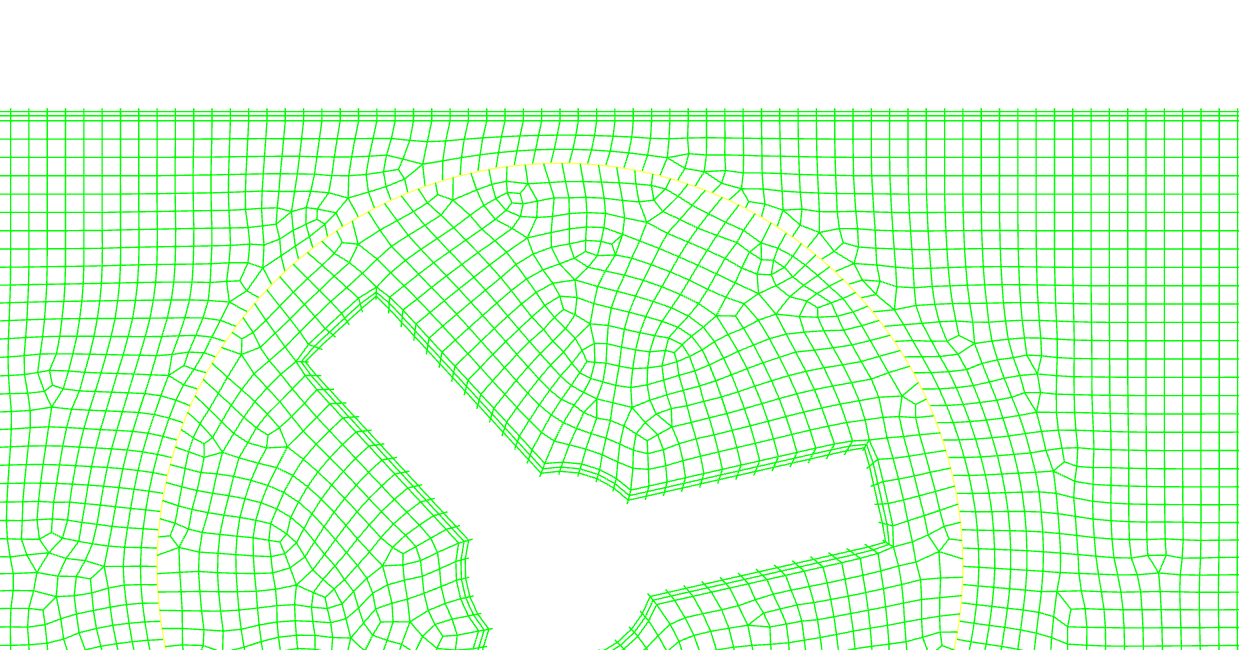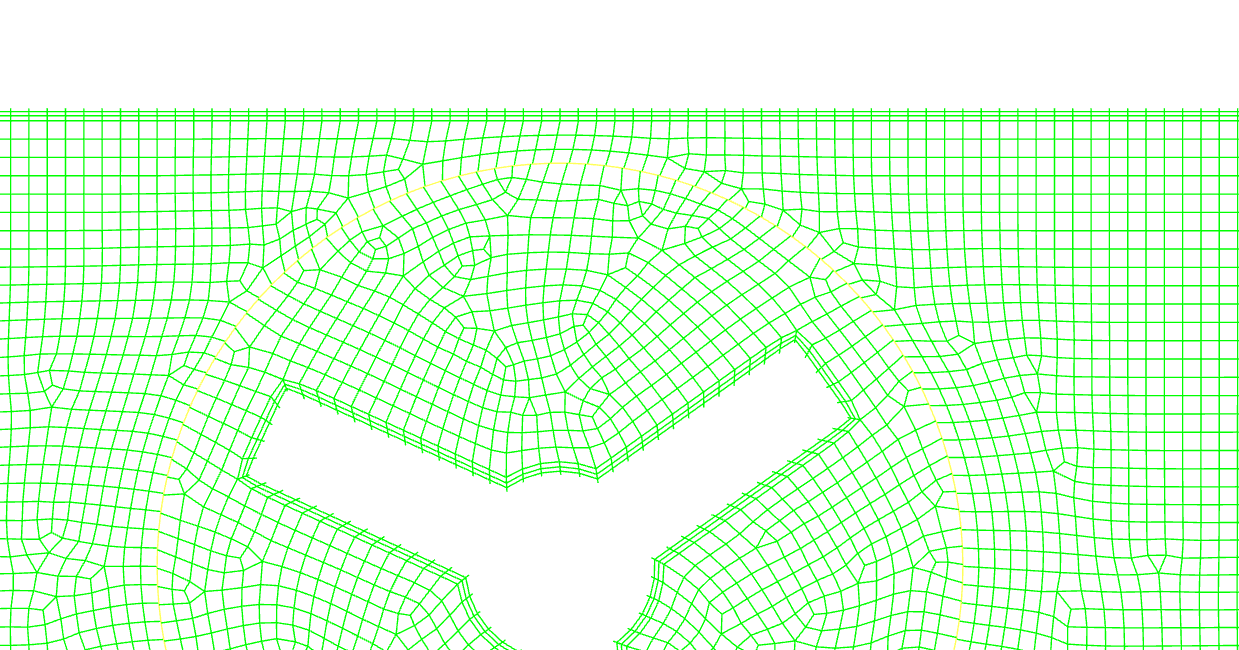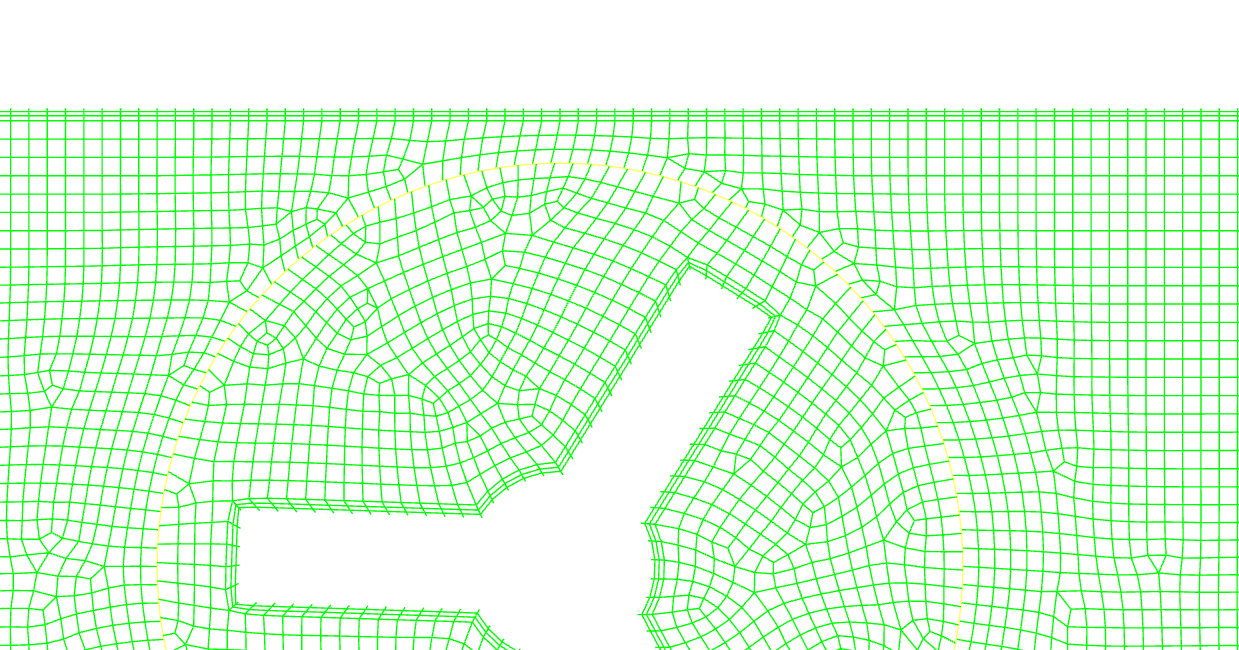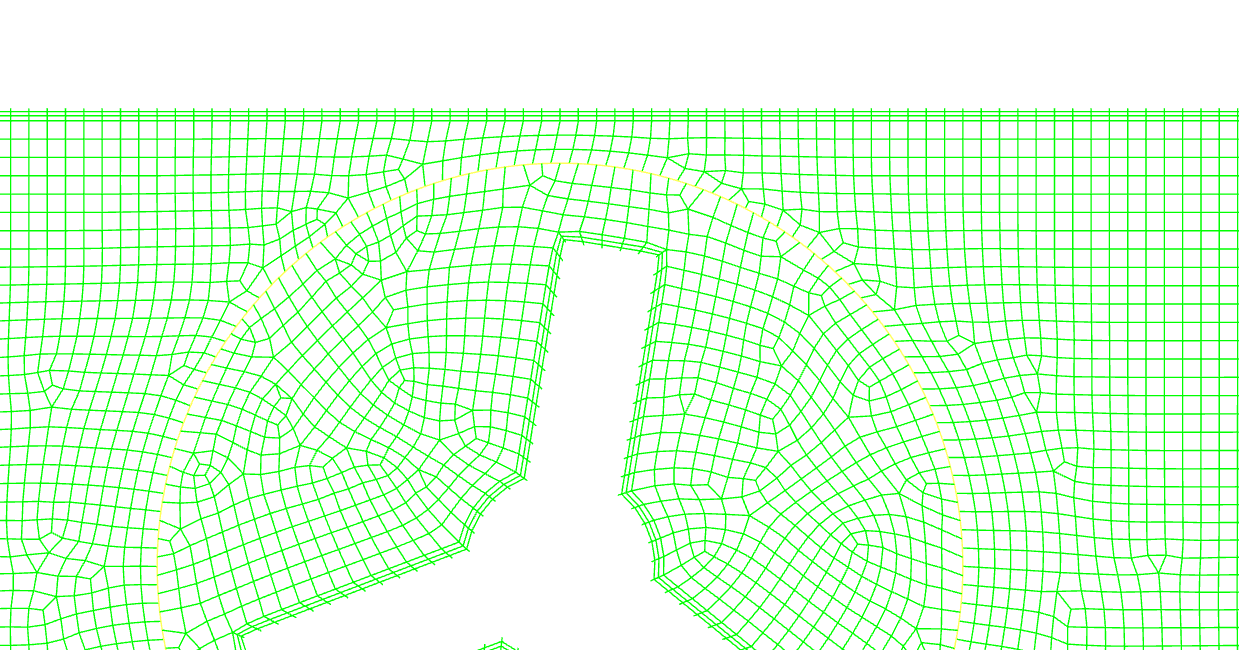
ズレたメッシュとそれ以外の領域との境界で情報を適切にやり取りすることで、動的な変化の様子を捉えることが出来ます。また、回転する構造に非対称性があっても、その影響を考慮することが可能です。実際に羽根が受ける力を再現して構造との連成を行う等の拡張的な用途もあります。

そもそもCFDで数値解析しない

身も蓋もないですが、メッシュを切ることが流体空間が逐次変わる回転機械と相性が悪いのであれば、そもそもメッシュが必要なCFDで流体解析をしない、といった抜本的な変更も視野に入れてもいいかもしれないでしょう。粒子法(流体の挙動を粒子の集まりとしてモデル化する手法)であれば、メッシュを切る必要がなく、この辺の課題からは解放されます。 もちろん粒子法は粒子法で別途課題があったりするので、そう簡単に万事解決とはならないかも知れませんが……

最後に

比較的我々にとって身近な流体と回転する機械の関係性ですが、それを真剣に数値解析で紐解こうとすると結構な厄介事となり、先人の方々が様々手を変え品を変え攻略しようとしてきた歴史が垣間見えます。皆さんも日常で流体の回転を使っているな、と感じたときに、このようなことも併せて考えてみるといいことがあるかもしれません。

Ref.

[1] Modern reconstruction of wind organ and wind wheel of Heron of Alexandria (1st century AD) according to W. Schmidt: Herons von Alexandria Druckwerke und Automatentheater, Greek and German, 1899 (Heronis Alexandrini opera I, Reprint 1971), p. 205, fig. 44; cf. introduction p. XXXIX

[2] Se-Woon Hong, In-Bok Lee, Il-Hwan Seo,”Modelling and predicting wind velocity patterns for windbreak fence design,”Journal of Wind Engineering and Industrial Aerodynamics,142,2015,pp 53-64.

[3] https://www.kyushu-u.ac.jp/f/45078/21_04_19_01.pdf