はじめに
こんにちは、エンジニアの夏目です。
2022年初頭、社内でベイズ最適化の勉強会をしていました。弊社NatureArchitectsは形から機能を設計する会社のため、3DCADとCAEを密に連携させた設計を得意としており、形状を探索するときに最適化をよく行います。
その勉強会の中で社長がポツリと一言、「3DCADで形状のベイズ最適化できたら面白いんじゃない?」と言いました。
その一言を受けてベイズ最適化ができるライブラリを探していたところOptunaを見つけ、OptunaのGrasshopper向けラッパー「Tunny」の開発を始めました。
ラッパーを開発していくにつれて、機能がより欲しくなりOptunaやOptuna Dashboardへコントリビュートを始めたところ開発者の方の目に止まり、今回OptunaとTunnyについてのブログを書かせていただきました。
日本語版はこの弊社ブログですが、英語版はOptuna公式のブログで公開しています。そちらも合わせて御覧ください
本記事は普段Optunaを触っている、または興味のある方に対しての記事になっています。対象読者の方は機械学習などの設計が専門でない場合が多いので、以下のような流れでTunnyについて紹介します。
- Tunnyと3DCADのRhinocerosについて
- CAEと最適化について
- Human-In-the-loopとCADの連携について
Optunaの主な使用例は機械学習のハイパーパラメータのチューニングですが、使われている技術は「ブラックボックス最適化」です。そのため、機械学習のハイパーパラメータのみが対象な技術ではありません。
「形」からうまれる「機能」というブラックボックスのパラメータの最適化を行うツール「Tunny」について紹介できればと思います。
Tunnyとは
Tunnyは3DCADのRhinocerosのノードエディタプラグインGrasshopper上で動くOptunaのラッパーになります。
以下のGitHubのリポジトリにてMITライセンスで公開しているOSSのソフトになります。
CADと最適化がどのように結びつくかわからない方も多いと思いますので、まずは簡単な動作の状況を見ていただければと思います。
ここでは与えられた曲面に対して、それを格子状の梁部材で構成した際に以下の2つの問題を解いています。
- 部材の長さの均一化(部材長さの標準偏差の最小化)
- ある特定の曲面(TargetSurface)との形状の差を最小化
中央付近にある赤枠の中で動いている白い四角い部分が変数になり、各数字が形状パラメータを表しています。
上記の動画で最適化をより進めた結果のOptunaの visualization.plot_pareto_front でのプロットが以下になります。DiffがTargetSurfaceとの形状の差、SD_Lengthが部材長さの標準偏差になります。Diffは形状を表すパラメータのユークリッド距離で求めています。
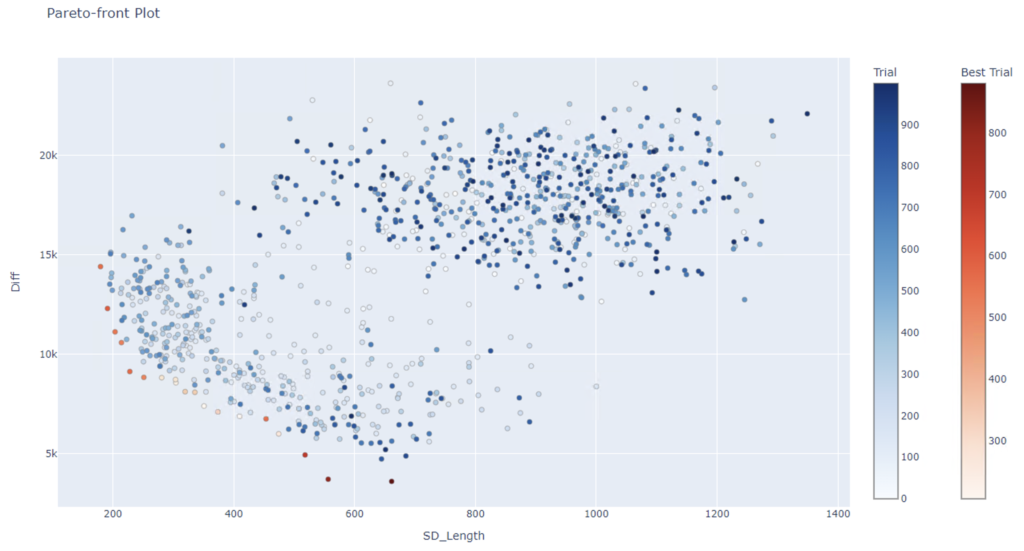
この例は建物の曲面形状の屋根だと考えるとわかりやすいかもしれません。
部材長さが複数あると加工手間などが増えコスト増に繋がります。それに対して部材長さを揃えることで製造のコストダウンに繋がりますが、建築家がデザインした理想の屋根形状(TargetSurface)とは異なる形になっていきます。
そのような関係をTunny(Optuna)を使うことで計算し可視化することができます。この結果は、「建設コスト」(施工容易性という機能)と「デザイン」(形状)という2目的関数をブラックボックス最適化で解いていると見ることもできます。
このような最適化はわざわざCADを使わなくともコーディングに精通していれば例えばPythonのみで行うこともできます。しかし、餅は餅屋です。
CADが得意な部分はCADで作成したほうがより効率的に最適化が行なえますし、Tunnyの対象はプログラマではなくCADを触る普通の設計者です。
プログラムを書くことなくGUIで設定するだけで、近年の最新のアルゴリズムも導入されて開発されているOptunaを使った形状の最適化が実行できる点が大きな強みになっています。
以降ではもう少しTunnyを構成する要素について、より詳しく紹介できればと思います。
なお本例は以下のAMDlabさんの例を少し変更して使わせていただきました。Tunnyの使い方に興味のある方はこちらも見ていただければと思います。
-【Grasshopper】Tunnyを使って最適化をやってみよう!
Rhinocerosについて
TunnyはRhinoceros(以降Rhinoと呼びます)のプラグインのGrasshopper上で動くものです。
RhinoはRobert McNeel & Associatesによって開発されている3次元CADソフトになります。特徴としてはNURBSモデリングに強い点が挙げられます。
NURBSはNon-Uniform Rational B-Spline(非一様有理Bスプライン)の略でスプライン曲線の一つで数式で形状を表す方法になります。そのため例えば車体や船舶、建築の外装のようななめらかな曲面を使用する分野でよく使用されています。
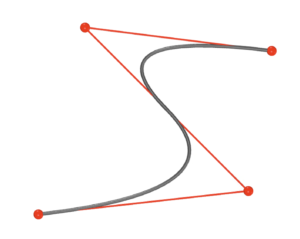
形状表現のイメージとしては以下が一例になります。
以下の灰色の曲線はNURBSで表現したものです。曲線は複数の制御点(赤丸)から構成され、制御点には重みが設定されており、その重みをもとにどの程度その点に影響を受けた線になるかを計算で求められ、一本の線になります。
具体的にはNURBS曲線C(u)は下式のようにk個の制御点P_iにおける重みw_iつきの基底関数N_{i, n}を使って形状が表現されています。
C(u) = \sum_{i=1}^{k}\frac{N_{i, n}w_i}{\sum_{j=1}^{k} N_{j, n} w_j}P_i
上記は曲線の式ですが、同様に曲面も表すことができます。
一方で例えばBlenderのような3Dモデラーではメッシュで形状を表します。これは3点または4点で構成される面の集合で形状を表すものとなり、形状の表現方法が異なります。
(なお、Rhinoはメッシュを、BlenderはNURBSを扱うこともできます。昨今の3Dを扱うソフトは基本的にはどちらも利用可能になっており、どちらを主眼に開発されているかの違いになります。)
Grasshopperについて
Grasshopper(以降GHと呼びます)はRhino上で動くノードエディタになります。処理の一つ一つがノード(GHではコンポーネントと呼びます)になっており、それらを組み合わせることで形状を作成することができます。
簡単な例だと以下のような四則演算や、制御点を指定してカーブを作成することができ、これらを組み合わせることで様々な形状を作成することができます。

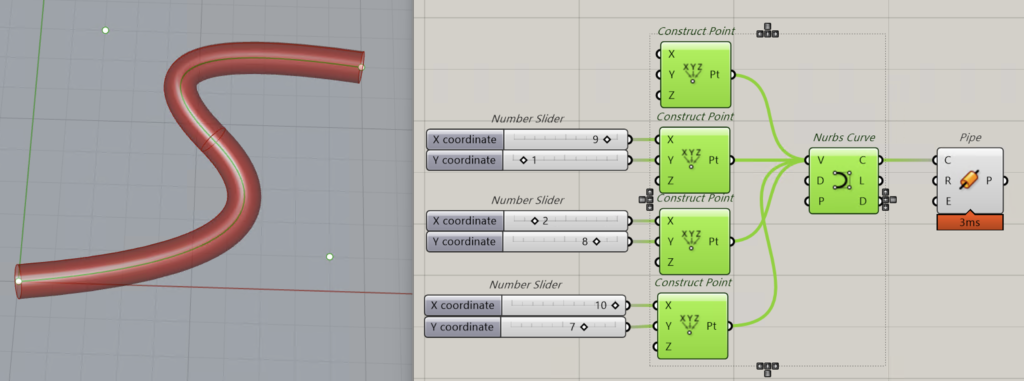
CADはマウスとコマンドを使ってGUIで一つ一つ処理していくイメージがあるかもしれません。ですがGHのコンポーネントはRhinoが提供するSDKを基に作られているため、Rhinoの形状処理をノードベースで行うことができ、これが大きな特徴です。
そのため一度、コンポーネントを使って形状生成アルゴリズムを作成すれば同様のアルゴリズムで複数形状を簡単に作成することができます。
複雑な形状でも同じアルゴリズムならば簡単に形状を微修正しながら形状検討ができたり、数式のようなルールベースで形状を作成していくことができます。こういった設計のアプローチはコンピュテーショナルデザインやアルゴリズミックデザインと呼ばれます。
冒頭であげた屋根形状の最適化の例で言えば、屋根面を表すNURBSの制御点の位置がGH上でパラメータになっており、この値を操作することで形状をコントロールしていました。
Optunaとの連携
RhinoとGHについて紹介したので、次に具体的なOptunaとの連携の実装について簡単に紹介します。
Optunaは最適化の設定をより柔軟に行える ask-and-tell インターフェースがあり、Tunnyもask-and-tellインターフェースを使って実装しています。
ask-and-tellインターフェースについてはOptuna公式のドキュメントを参照してください。
RhinoとGHはC#で書かれて動作しており、同様にTunnyもC#で開発していますが、OptunaユーザーにもわかりやすいようにここではPythonのような疑似コードを上げます。
実際はPythonnetというC#からPythonを実行できるライブラリを使用しているので、興味のある方はそちらもご確認ください。
import optuna
study = optuna.create_study() # studyの作成
while(true):
if CheckOptimizationComplete(): # GHのUIで設定した値を使って終了判定
break
trial = study.ask()
variable = trail.suggest_float(....)
# ここでoptunaからサジェストされた値をGHに反映し、結果を取得
score = EvaluateGrasshopper(variable)
UpdateUI() # GHのUI(例えばプログレスバー)の更新
study.tell(trial, score)
ask-and-tellインターフェースを使うことで、1トライアルの間にC#とPython間の連携、UIの更新などの処理を柔軟に入れ込めるため、他の最適化ライブラリを使うよりも開発をスムーズにすることができました。
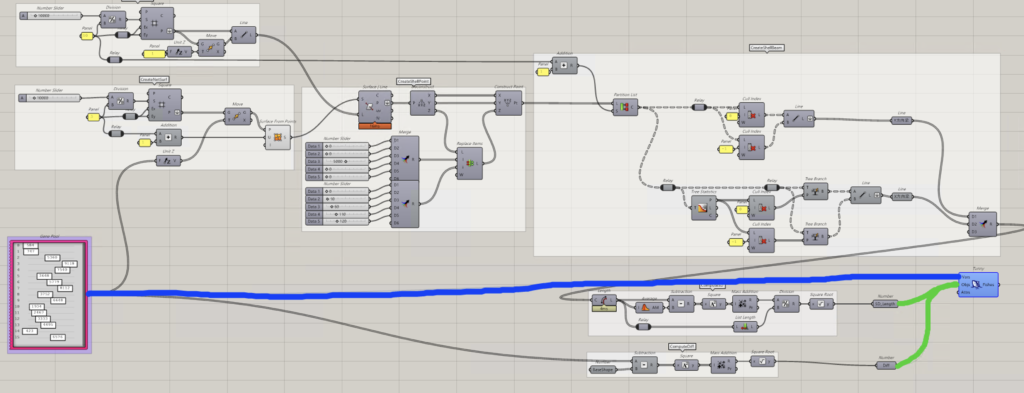
上記の流れの中で、EvaluateGrasshopperメソッドの部分の処理はGHの動作になります。冒頭で上げた屋根形状の最適化では以下のようなGHのファイルが動作しています。
右下の青色のTunnyのコンポーネントに対して青色のラインで繋がれたものは最適化での変数、緑色のラインで繋がれたものは目的関数の戻り値として認識されます。
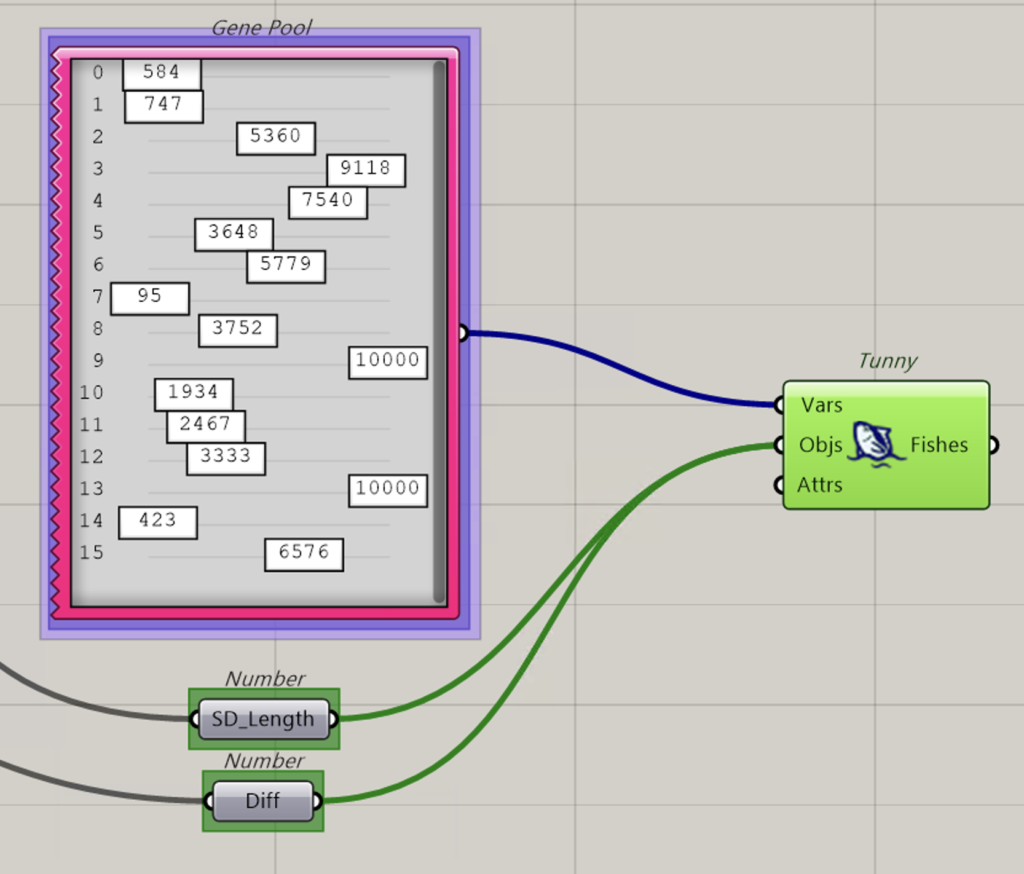
変数と目的関数の戻り値の接続だけを拡大したものが以下です。
コードとGHとの連携した処理を行っているEvaluateGrasshopperメソッドの流れとしては以下になります。
- コードの中でEvaluateGrasshopperメソッドが呼ばれたとき、Optunaのtrial.suggest_float()で提案された値をGHのTunnyコンポーネントが受け取る
- 青色で繋がれたパラメータをまとめたコンポーネント(上記GenePoolと記載されたコンポーネント)に値が反映される
- GH上に提案された値が反映されると、変数のコンポーネントにつながる他のコンポーネントの計算が実行され、その結果が緑色でObjsに繋がれているSD_LengthとDiffと表示されたコンポーネントに反映される
- Tunnyコンポーネントに渡されたSD_LengthとDiffの値がEvaluateGrasshopperメソッドの戻り値としてコードに渡され、objectiveに反映される
このようにTunnyはGHの処理をOptunaの最適化処理の一部として使用することで、CADとOptunaの連携を実現しています。
簡単な連携の例
冒頭で上げた形状処理の入った連携ではわかりづらい部分もあると思いますので、単純な数式を対象にした場合の最適化の実行例を以下に上げます。
まずはPythonで書く場合です。
import optuna
def objective(trial):
x = trial.suggest_float("x", -15, 30, step:0.01)
y = trial.suggest_float("y", -15, 30, step:0.01)
c0 = (x - 5) ** 2 + y ** 2 - 25
c1 = -((x - 8) ** 2) - (y + 3) ** 2 + 7.7
trial.set_user_attr("constraint", (c0, c1))
v0 = 4 * x ** 2 + 4 * y ** 2
v1 = (x - 5) ** 2 + (y - 5) ** 2
return v0, v1
def constraints(trial):
return trial.user_attrs["constraint"]
sampler = optuna.samplers.TPESampler(constraints_func=constraints)
study = optuna.create_study(
sampler=sampler,
study_name="study1",
directions=["minimize", "minimize"]
)
study.optimize(objective, n_trials=32, timeout=600)
上記コードをTunnyを使って表現すると以下のようになります。
変数をVars(Variables)、目的関数をObjs(Objectives)、属性をAttrs(Attributes)につなぐことでOptunaに映されます。
最適化のトライアル数やタイムアウトの時間、スタディ名、サンプラーの種類などは右側のUIから選択できるようになっています。
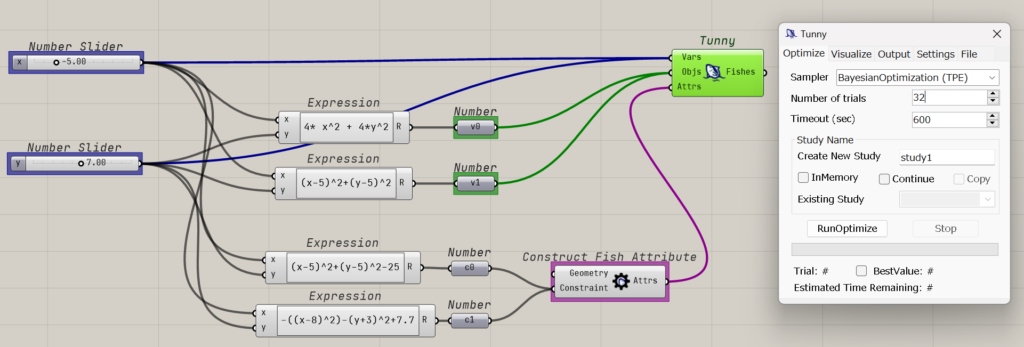
右側のフォーム中の「RunOptimize」を押すとOptunaを使った最適化が実行されます。
最適化の実行後はOptunaのStorage(SQLite3とJournalStorageに対応)を使うことができるため、結果を読み取り、可視化の対象を指定することでTunny上からOptunaのvisualizationの各関数を呼び出して図を表示します。
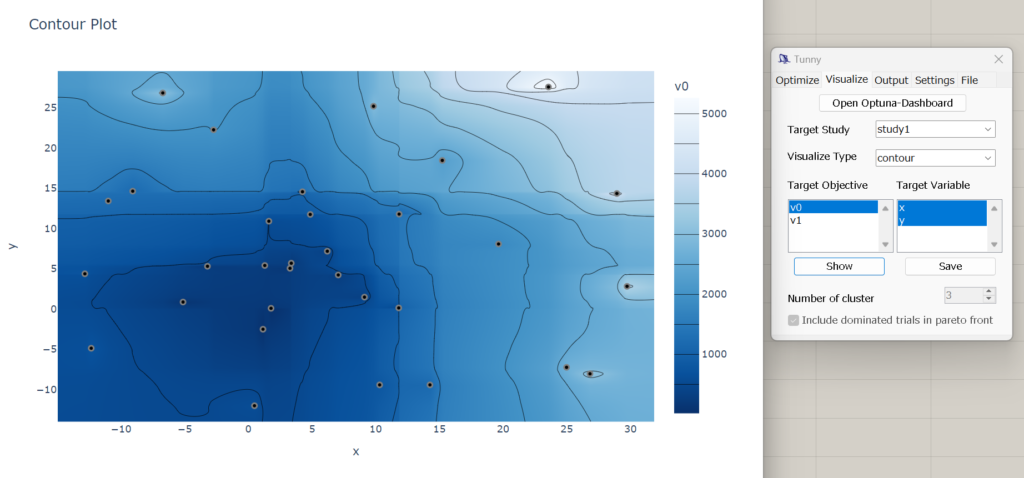
Optuna Dashboardにも対応しているため、GHで最適化が動作しているときの結果をリアルタイムに取得することもできます。
CAD連携と書きましたが、このような例からわかるようにOptunaのノードベースのUIといった方がわかりやすいかもしれません。
CAEと最適化
Tunnyの構成要素について紹介したので、ここからはより具体的なTunnyの使用例を紹介します。
Optunaのユーザーの皆様は最適化の適用先を考えたとき、機械学習のハイパーパラメータ最適化を最初に考えるかもしれませんが、ここでは最適化を車の部材の設計に適用する例について紹介します。
部材の設計する際は解析で荷重に対する安全性などを検討します。検討の際に使用する計算機を使用した設計支援ツールのことをCAE(Computer Aided Engineering)と呼びます。
より具体的には構造解析であればFEM(Finite Element Method:有限要素法)などの手法を使って解析を実施するツールを指します。
ものづくりのベースとして、実物を作り実験を行い性能を確認となりますが、近年では設計の高効率化、ノウハウだけによらない形状のより発見的な探索、リードタイムの短縮化などの需要が高まっており、実験でのトライアンドエラーを行うよりも前に解析でより有望な形状を発見することがより期待されてきています。
そのため、コンピューター上で形状の検討を行うことができるCAEと形状探索支援としての最適化の組み合わせが行われるようになっています。
弊社Nature ArchitectsではGH上で「解析モデルの形状生成」→「解析の実施」→「最適化」の一連の流れが非常にスムーズに実行できる環境を開発しており、最適化の部分でOptunaを利用して作成したTunnyを使用しています。
ここではCAEを使用した設計の例として、弊社で行った自動車のフロントの衝突時の衝撃吸収部材フロントバンパの設計例について紹介します。
フロントバンパの設計
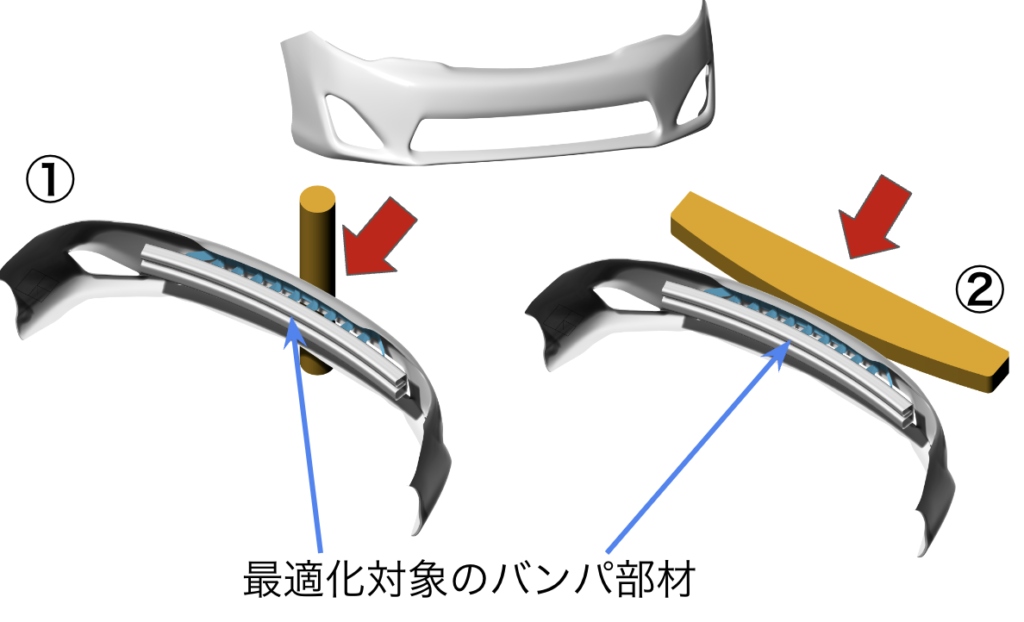
対象部材は以下のような車のフロントバンパの部材です。本例では、この部材は以下の2つの安全基準を満たすことを設計要件とします。
- 歩行者への衝突時(時速40km程度)の歩行者脚部保護
- 車同士の軽衝突(時速10km程度)時の車の保護
本例では、1 は足を模擬した円筒、2は車のフロント部分を模擬した扇状部材を衝突させる解析を行うことで安全性の評価を行います。
どのような現象を対象にしているかわかりやすくするために上記2つの解析結果の1例を以下に示します。
歩行者脚部の衝突
車同士の軽衝突
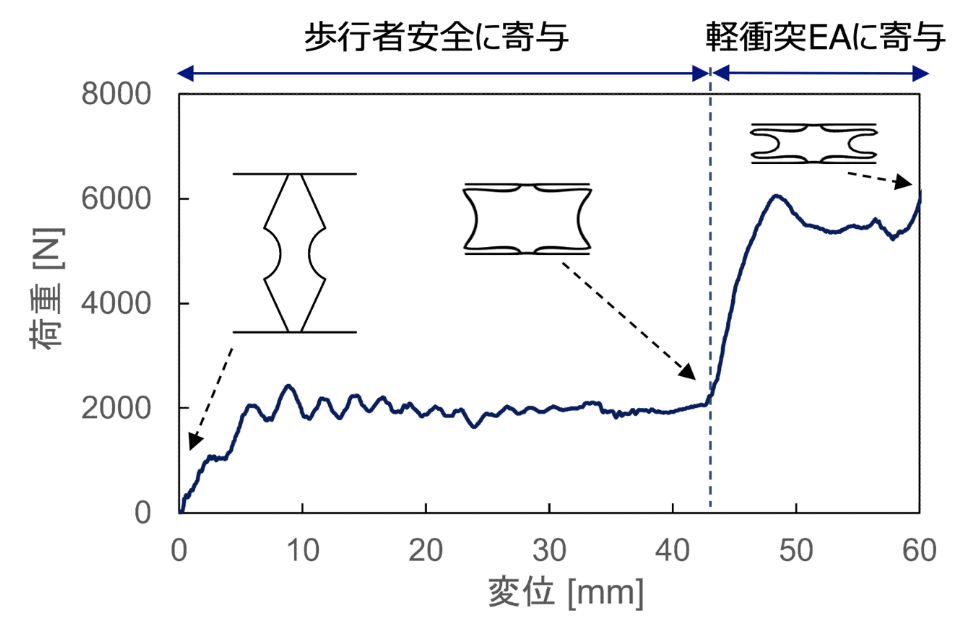
歩行者保護は例えばエアバッグの事例を考えると理解しやすと思いますが、極力柔らかいものでぶつかり衝撃を和らげる必要があります。
一方で、自動車同士の衝突は大きなエネルギーが発生するため、極力固いもので衝突した後に大きく変形し、そのエネルギーを効率的に吸収することが期待されます。
このように衝突という1つの事象に対して2つの相反する性能を満たすことが要求される設計要件になっています。
また安全性能であることから単なる安全性の最大化問題ではなく、必ず満たさなければならない最低の性能が規定されています。
そのため制約条件付きの多目的最適化でこの問題を解くことを行いました。
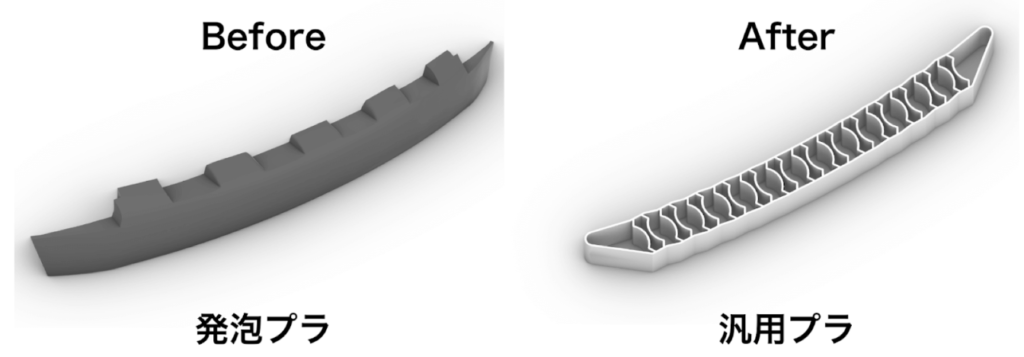
既存のバンパ部材の多くは以下の左にあるような発泡プラスチックの塊を加工して作成されています。
Nature Architectsでは環境負荷の低減やコスト削減を行うために、発泡プラスチックと同等の機能を材料の塊ではなく、汎用プラスチックを使った「形状」で実現する設計を行いました。
その設計の中で、形状探索にTunnyを使用しています。
最適化を行う形状は、社内の事前検討により以下のような砂時計型のユニット形状がこの条件に有望だと判明しました。
その部材をフロントバンパーの形状に適用した実スケールでの衝突時性能を評価しました。
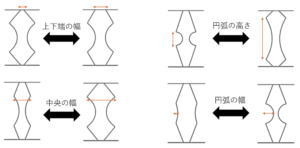
最適化は砂時計形状に対して以下の4つパラメータ及び板厚と奥行きの合計6を設定して行っています。
次に最適化に使用したサンプラーについてです。
自動車の衝突の解析は計算コストが高い部類の解析になります。計算時間がかかることから、短い設計期間の中であまり多くのトライアルを試行できないため、少ないトライアル数で最適解を発見しやすいベイズ最適化(TPE)を選択しました。
Optunaは複数のサンプラーを提供しているため、問題に合わせて適切なサンプラーを選択することができます。
最適化を実行した結果は以下になります。いくつか代表的な結果の形状をピックアップしています。

この設計例ではTunnyを持ちいた多目的最適化を実施することで、上図の左下に位置する2つの安全性能を満たす部材形状を発見することができました。
Tunny(Optuna)を使った形状の最適化によって、コスト削減や環境負荷の少ない形状探索の可能性を確認することができました。
Human-in-the-loopを使ったCADでの形状探索
Optuna Dashboardではv0.10からHuman-in-the-loop最適化がサポートされました。
Optuna Dashboardのページでは簡単な例としてrgbの3つの値をパラメータを設定して生成された色が夕焼けの色に似ているかの判定を使った最適化をしています。
他の使用方法としては、例えばStableDiffusionのような画像生成AIへ入力するプロンプト最適化が以前のミートアップでは挙げられていました。
ここにCADとの連携が加わると面白いことができるようになります。
TunnyではOptuna Dashboardを使ったHuman-In-the-loopが実行可能になっており、以下で2つの例を紹介します。
花瓶形状の最適化
まずは簡単な事例として花瓶形状のHuman-in-the-loop最適化の例を上げます。
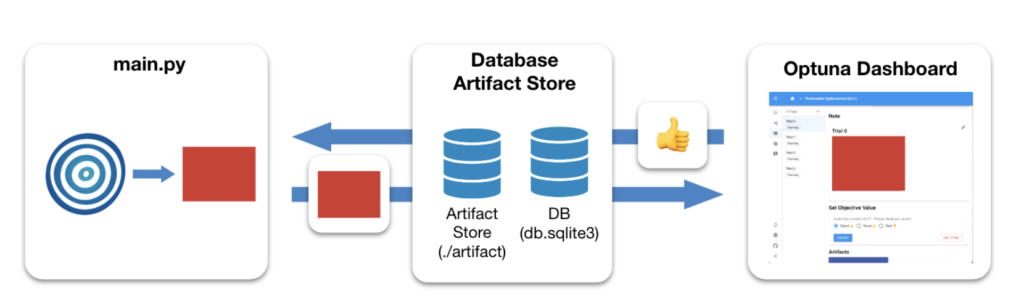
TunnyではHuman-In-the-loopの設定を行うとRhino上のモデルを保存し、OptunaのArtifact(最適化での生成物)とすることができます。
以下ではRhino上に表示されているモデルのビューを画像で保存し、ArtifactとしてOptuna Dashboard上でスライダーを使って評価する仕組みが実行されています。
花瓶は4つの円をなめらかな面でつなげるように作成しており、円の半径と中央にある2つの円の高さの合計6パラメータ対象に最適化を行っています。

単純な形状生成アルゴリズムですが、多様な花瓶形状が生成されていることが上記の動画からわかります。Human-In-the-loopによって個人の好きな花瓶形状を見つけことに役立つと思われます。
上記は花瓶の3Dモデルから得られた画像を使った最適化ですが、裏で動いているのものはCADです。そのため画像にする際に補助的な情報として輪郭情報や深度情報を容易に計算することができます。
そのような情報を Control Net などの技術と組み合わせることで対象形状は直接的に操作し、背景などは画像生成で作成など手法の組み合わせでも効果を発揮すると考えています。
例えば建物形状はデザイナーがCADでパラメータを決めた形状とし、CADを使って直接形状生成を行いながら、背景を画像生成AIで作成することで、検討段階で複数の建物パースが効率的に生成できる可能性があります。
CAEとHuman-in-the-loop
製造業において多くの場合は、デザイナーと構造や電装、空調などを設計するエンジニアは分業体制を取っています。
どちらかといえば前者は個人の感性、後者は数式などの理論から導き出される値を扱います。そのため、これまで設計での最適化を行う場合の多くは後者のみを対象に扱っていました。
例を挙げると構造解析から求まる部材の安全性の最大化や熱解析による空調時のエネルギー効率の最適化などです。
これらの最適化に加え、Human-In-the-loopを行うことでデザイナーの感性も含めた設計全体の最適化を行える可能性があります。
以下は建物と柱配置の例です。
部屋(ボックス)に柱がかぶらない制約条件のもとで構造解析を実施し、建物安全性を解析で確認しています。
建物モデルのカラーコンターは地震時の建物に発生する力の分布です。赤色なほど高い力が発生しています。
この構造的な評価に加えて、建物デザインとしてどこに柱があればよいかはデザイナー(また施主)の嗜好が存在します。
そこで目的関数に、柱配置を確認するための「建物モデル形状」と「地震時の建物の安全性(ひずみエネルギー)」の多目的最適化を実施しています。
この例は建物に対してですが、例えば車の外形についてもこの技術を活用できることが考えられます。
車のデザインとして外装の形状は非常に重要です。一方で車は走行時に風による抵抗が発生するため、あまり抵抗の大きな形状にすると、燃費の低下を招きます。
そのため、「デザインされた形状」と「走行時の抵抗」の多目的最適化によってより効率よく車体の外装設計ができる可能性があります。
おわりに
長くなりましたが以上になります。
最後に紹介したHuman-In-the-loopはとてもおもしろい技術ですが、評価に時間がかかるという問題があります。
最適化で十分なトライアルが100個だとすると、1回の人間の評価に30秒かかっていれば合計で50分もかかり、なかなか人が最適化のループに入るのは大変かもしれません。
ですがより効率的に評価できる手法も研究されており、今後の発展に期待しています。
本記事を読んでGrasshopperを使ってはじめて最適化を行ってみたいと考える方もいるかも知れません。
他の最適化コンポーネントでは資料が英語なため、なかなか始めづらいのですが、Tunnyは日本語でOptunaの解説の本が出ているため、理論についての勉強もしやすいことも大きな特徴です。
TunnyはOSSで開発しています。もし興味のある方はGitHubのページでIssueやDiscussionsなどから気軽にお問い合わせください。
もちろんコントリビュートも大歓迎です。
Optunaの一つの使い方として本記事が参考になれば幸いです。
最後までお読みいただきありがとうございました。