皆さんKaramba3dは好きですか？私はとても好きで愛用しています。
Karamba3dは3D CADのRhinocerosのノードエディタ"Grasshopper"で動く構造解析プラグインです。
このプラグインはRhinocerosのモデリング機能と密接に結びついているため、1つのソフト内で複雑形状をパラメトリックに作成し、それをそのまま構造解析できる点が非常に強い特徴となっている構造解析ソフトです。
[公式サイト](https://karamba3d.com/learn/examples/)を見るとサンプルファイルもかなり充実しており、Karamba3dを使った解析のやり方がわからない場合にも参考が多く非常に助かります。
解析ソフトで気になるのは解析の性能です。Karamba3dはAnsysのようなの有名な商用CAEソフトではないため、例えば精度について気になります。
しかしこういった情報はあまり見ないため、本記事では簡単なモデルを対象に確認していきます。
# 比較対象
Karamba3dのBeam要素とShell要素を、AnsysのShell要素とSolid要素と比較します。
# モデル化
ソルバーの違いのみを確認できるよう、極力パラメータは揃えて解析を実施します。
## パラメータ
- ヤング率： `$ 2.0×10^5 \textrm{N/mm}^2 $`
- ポアソン比：0.3
- 長さ：10.0mm
- 密度：`$ 7.85 \textrm{g/cm}^3 $`
- メッシュサイズ：0.25mm程度になるようにメッシング、梁要素も0.25mm程度に分割
- 断面：1mm × 1mm の矩形
- 梁ならば矩形断面、シェルならば1mmの板厚を与えています。
メッシュは以下のものを使用しています。Ansysは四角形要素も使うことができますが、Karamba3dは三角形要素しか扱えないため、条件を揃えるために三角形要素のみで比較しています。
## 比較パターン
以下の8パターンで解析を実施し、結果を比較します。
- Karamba3d
1. Beam要素（KrBe）
1. Shell要素 面内曲げ (KrSh-in)
1. Shell要素 面外曲げ (KrSh-out)
- Ansys
1. Shell要素 面内曲げ 1次要素(AnSh1-in)
1. Shell要素 面内曲げ 2次要素(AnSh2-in)
1. Shell要素 面外曲げ 1次要素(AnSh1-out)
1. Shell要素 面外曲げ 2次要素(AnSh2-out)
1. Solid要素 6面体2次要素(AnSol)
# 片持ち梁の先端荷重
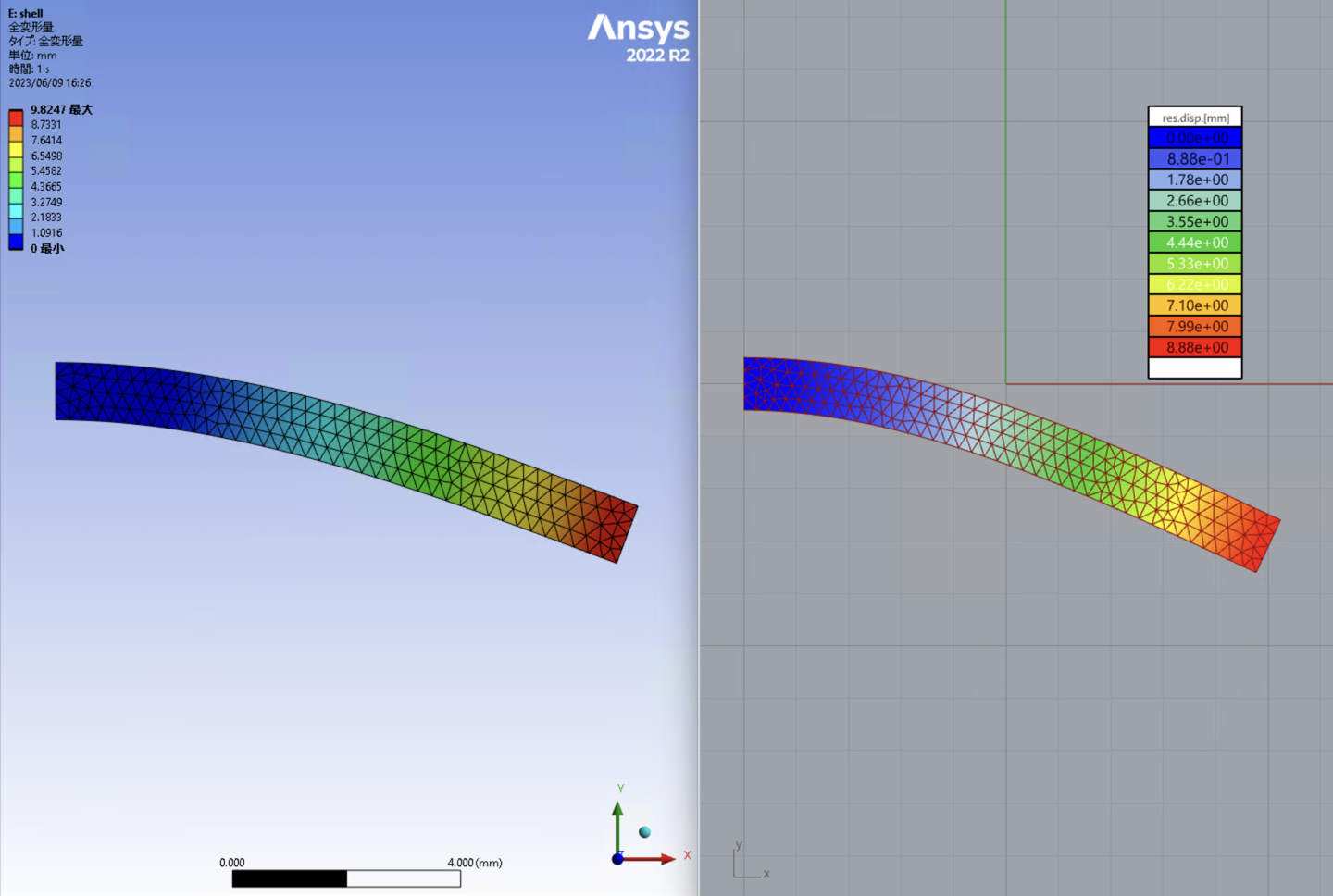
では実際に解析を行っていきます。
## 境界条件
以下のように基端を固定、先端に荷重をかける片持ち梁の問題を解きます。
## 解析時間の計測
Karamba3dは解析速度が高速ということが知られていますので、その点も比較できるように、解析時間についても確認します。
解析時間は以下の値を使用しています。
- Ansysの解析時間：Elapsed time spent computing solution の値
- Karamba3dの解析時間：解析実施のコンポーネントの処理にかかった時間
- 線形解析であれば Analyze(Karamba3D)
### 線形静解析
予想値は以下の式で求めています。
荷重の値`$P$`は500Nとしています。
```mathjax
\delta = \frac{PL^3}{3EI}, \quad
\sigma = \frac{M}{Z}
```
#### 解析結果
解析結果は以下になりました。
| 微小変形 | KrBe | KrSh-in | KrSh-out | AnSh1-in | AnSh1-out | AnSh2-in | AnSh2-out | AnSol | 予測値 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 先端たわみ [mm] | 10.1 | 8.9 | 9.9 | 8.8 | 10.0 | 9.8 | 10.0 | 10.0 | 10 |
| 予測値との差 | 0.8% | -11.2% | -1.1% | -12.0% | 0.1% | -1.8% | 0.3% | 0.3% | - |
| 最大相当応力 [MPa] | 30000 | 27608 | 29276 | 23302 | 29026 | 28732 | 35425 | 30914 | 30000 |
| 予測値との差 | 0.0% | -8.0% | -2.4% | -22.3% | -3.2% | -4.2% | 18.1% | 3.0% | - |
| 計算時間 [s] | 0.004 | 0.013 | 0.014 | 0.1 | 0.1 | 0.1 | 0.1 | 0.5 | - |
| 計算時間比 | -99.2% | -97.4% | -97.2% | -80.0% | -80.0% | -80.0% | -80.0% | - | - |
Karamba3dのShell要素は1次要素に分類されるもので、結果を見るとAnsysの1次要素と同程度の精度を持っていましたが、2次要素程の精度はない事がわかりました。
計算時間についてはAnsys側の表示が1/10秒までのため、細かな比較はできていませんが、Karamba3dのほうが高速に結果が得られています。
なお表中の数字は読みやすいように丸めていますが、比率の計算は実際の解析から得られた桁数を使っています。
### 大変形解析
次に大変形解析です。Karamba3dではAnalyze Nonlinear WIPを使用しています。
荷重などの境界条件は同様としています。
使うソルバーを大変形ソルバーにしたのみが差になります
#### 解析結果
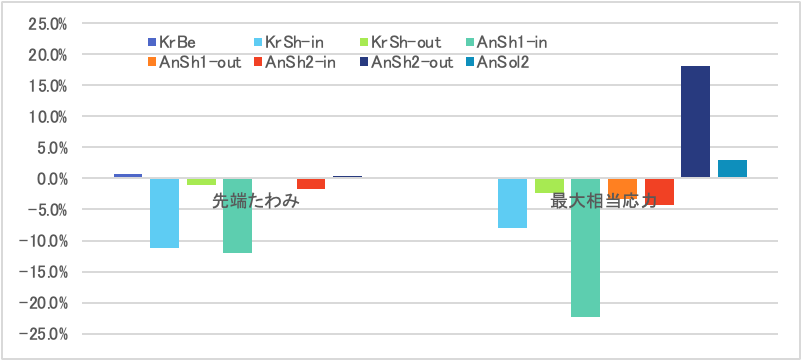
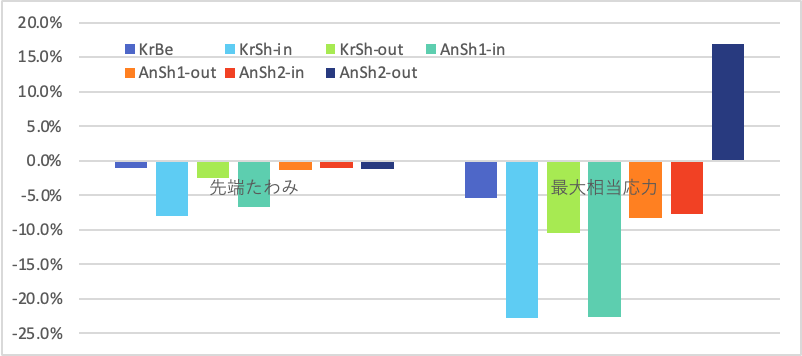
大変形については予測値を求めていないため、表中の比率はAnsysのソリッド要素の結果との差を示しています。
| 大変形 | KrBe | KrSh-in | KrSh-out | AnSh1-in | AnSh1-out | AnSh2-in | AnSh2-out | AnSol |
| --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 先端たわみ [mm] | 6.60 | 6.13 | 6.50 | 6.23 | 6.58 | 6.60 | 6.59 | 6.67 |
| 予測値との差 | -1.1% | -8.0% | -2.5% | -6.6% | -1.4% | -1.0% | -1.2% | - |
| 最大相当応力 [MPa] | 22300 | 18200 | 21100 | 18235 | 21607 | 21747 | 27546 | 23564 |
| 予測値との差 | -5.4% | -22.8% | -10.5% | -22.6% | -8.3% | -7.7% | 16.9% | - |
| 計算時間 [s] | 0.15 | 0.41 | 0.52 | 0.9 | 1.2 | 1.2 | 1.5 | 24.5 |
| 計算時間比 | -99.4% | -98.3% | -97.9% | -96.3% | -95.1% | -95.1% | -93.9% | - |
# ねじり荷重
片持ち梁の曲げについて確認したので、次に梁の先端へねじりモーメントを与えたときの結果について確認していきます。
## 境界条件
以下のように梁の先端をねじる荷重を設定します。
Karamba3dは節点へのモーメント荷重はありますが、先端の複数の節点に対して剛体接続やMPC設定し、中心の節点にモーメントを与える機能はありません。
そのためKaramba3dのシェル要素でねじり荷重をかける際は、先端が一様にねじれるように先端に剛な梁要素を設けてその中心にモーメントをかけています。
AnsysのモデルについてはMPCを設定して、断面の中心に対してモーメントをかけています。
荷重の値は20Nmmとしています。
## 解析結果
結果は以下のようになります。微小変形で解析を行っています。
ここから、Karamba3dのシェル要素はねじりが硬いことがわかります。
解析時間については、線形解析なので先端荷重時と大きく変わらないことが想定されるため省略しました。
| ねじり | KrBe | KrSh | AnSh1 | AnSh2 | AnSol |
| --- | --- | --- | --- | --- | --- |
| 先端ねじり角 [deg] | 1.01 | 0.44 | 0.94 | 1.09 | 1.06 |
| ソリッドとの差 | -5.1% | -58.3% | -10.8% | 2.6% | - |
# 固有値解析
Karamba3dは固有値解析も行うことができます。
これまでの静解析でわかった剛性のモデル化に加え、質量も含めたモデル化について確認するため、固有値解析も実施しました。
## 予測値の計算
各予測値は以下の式で求めています。添字が`$b$`のものが曲げに関する固有振動数、`$t$`のものがねじりに関する固有振動数になります。
なお、ねじり定数`$J$`は対象が矩形断面であることから下式の近似値を使っています。
```mathjax
n_{b1} = \frac{1.875^2}{2\pi L^2}\sqrt{\frac{gEI}{\rho A}}, \\
n_{b2} = \frac{4.694^2}{2\pi L^2}\sqrt{\frac{gEI}{\rho A}}, \\
n_{b3} = \frac{7.855^2}{2\pi L^2}\sqrt{\frac{gEI}{\rho A}}, \\
n_{t1} = \frac{\pi}{2L}\sqrt{\frac{gGJ}{\rho I_p}}, J = \frac{0.422}{3}a^4
```
## 境界条件について
境界条件は、これまで行ってきた解析と同様に基端を固定としています。
## 解析時間について
固有値の解析時間は10個のモードを抽出するまでの時間としました。
## 解析結果
結果は以下のようになります。
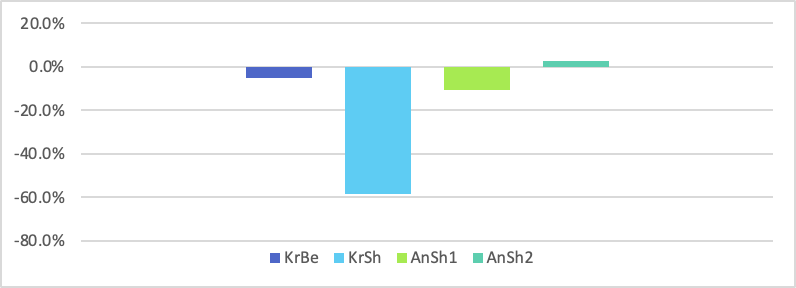
結果は面内の曲げ、面外の曲げ、それぞれの1次と2次モードとねじりの1次モードの合計5つの固有値について比較しました。
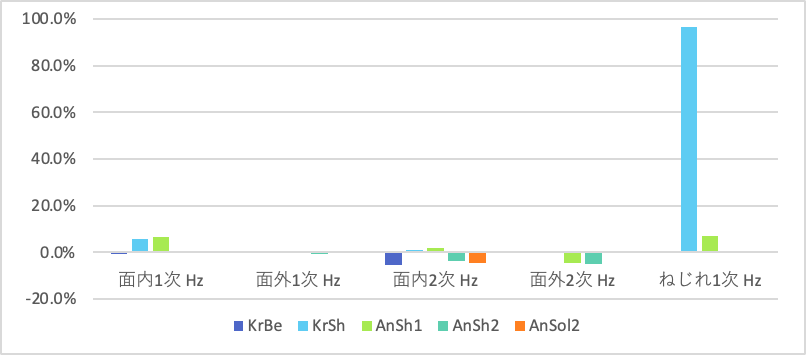
上のグラフではねじり以外の結果が分かりづらいため、拡大したものが以下です。
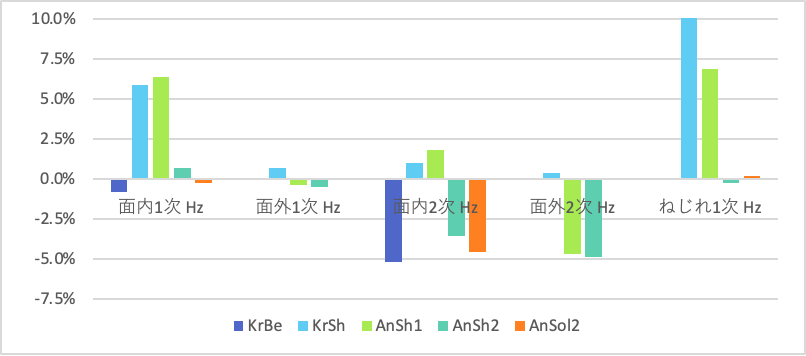
| 固有値 | KrBe | KrSh | AnSh1 | AnSh2 | AnSol | 予測値 |
| --- | --- | --- | --- | --- | --- | --- |
| 面内1次 [Hz] | 8089 | 8633 | 8673.8 | 8210 | 8132 | 8153 |
| 予測値との差 | -0.8% | 5.9% | 6.4% | 0.7% | -0.3% | - |
| 面外1次 [Hz] | - | 8208 | 8123.5 | 8113 | - | - |
| 予測値との差 | - | 0.7% | -0.4% | -0.5% | - | - |
| 面内2次 [Hz] | 48441 | 51603 | 52038 | 49277 | 48770 | 51097 |
| 予測値との差 | -5.2% | 1.0% | 1.8% | -3.6% | -4.6% | - |
| 面外2次 [Hz] | - | 51305 | 48710 | 48609 | - | - |
| 予測値との差 | - | 0.4% | -4.7% | -4.9% | - | - |
| ねじり1次 [Hz] | 71917 | 141487 | 76824 | 71712 | 72020 | 71896 |
| 予測値との差 | 0.0% | 96.8% | 6.9% | -0.3% | 0.2% | - |
| 計算時間 [s] | 0.012 | 0.036 | 0.3 | 0.3 | 0.6 | - |
| 計算時間比 | -98.0% | -94.0% | -50.0% | -50.0% | - | - |
固有値解析結果からもわかりますが、曲げについてはAnsysの1次要素程度の精度であることに対して、ねじり荷重時の解析と同様にKaramba3dのシェル要素はねじりが硬いことがわかります。
# まとめ
より正確に調べるためにはメッシュの分割数を変化させたり、解析速度の測定は1度ではなく複数回行った値を確認するなどの必要があリますが、概ねの傾向は本記事でわかります。
Karamba3dの梁要素については高い精度、シェル要素については必ずしも予測値に近い値でないこと、解析速度については非常に高速であることがわかったと思います。
そもそもGrasshopperで構造解析を実施する場合の多くは、初期検討でのパラメータースタディなどの多くの解析モデルを高速に回したいという状況なのではないでしょうか。
そのような状況を考えれば、初期検討において十分な精度で非常に高速という特徴はGrasshopperでの構造解析用途の需要にとても合致しています。
結果が予測値とピッタリ合わないからだめではなく、弊社ではこういった知見を元に、各設計内容やフェーズごとに求められるレベルに合わせた適切なソフトを選択することで、より良い設計を目指しています。
# 補足
Karamba3dのShell要素について興味がある方は、Karamba3dの公式サイトに記載のある以下の論文を参照してください。
- [Tric: a simple but sophisticated 3-node triangular element based on 6 rigid.body and 12 straining modes for fast computational simulations of arbitrary isotropic and laminated composite shells.](https://www.sciencedirect.com/science/article/abs/pii/S0045782596012339)
- J.H. Argyris, L. Tenek, and L. Olofsson.
- Comput. Methods Appl. Mech. Engrg., 145:11–85, 1997
- [The tric shell element: theoretical and numerical investigation.](https://www.sciencedirect.com/science/article/abs/pii/S0045782599000948)
- J.H. Argyris, M. Papadrakakis, C. Apostolopoulou, and S. Koutsourelakis.
- Comput. Methods Appl. Mech. Engrg., 182:217–245, 2000
