はじめに
本記事では下記のような読者を想定し、3~4章程度の構成を予定しています。
- Rhinoceros+Grasshopperに興味がある方
- Rhinoceros+Grasshopperを使う上で内部処理に関する理解を深めたい方
- Rhinoceros+Grasshopperを業務/研究/趣味などのために独自拡張して使いたい方
- メタマテリアルを設計して遊びたい方
1章はRhinoceros自体についての解説になりますが、Grasshopperを拡張して利用していくために重要であるため、後半は実装やデータ構造に近い話を含みます。
また、次章以降ではGrasshopperの実装に近い話をするので、何かしらのプログラミング言語、できればC#を知っているとより読みやすいかと思います。
Rhinocerosについて
Rhinoceros(以下Rhino)は、プロダクトデザイン・建築・ジュエリーデザイン・機械設計を含む多岐にわたる用途で使われている3DCADです。NURBSを主とした形状の編集のための高度な処理が多く提供されており、次章以降触れるGrasshopperはRhinoを複雑にコントロールするためのプラグインという関係性になっています。
通常のCADとしての利用→Grasshopperを用いた利用→プラグイン開発、と進んでいくにつれてRhinocerosの挙動やデータ構造を理解しておくことが重要となるので、少し踏み込んだ解説を含みます。
特徴
形状の処理そのものにフォーカスした思想
歴史的には船舶デザインのために開発された経緯があるようですが、現在では世の多くの用途を絞ったCADに比べて用途に特化した機能がほとんど無く、「形状の自由な編集」そのものに重きを置いたソフトウェアとなっています(個人的推しポイント)。
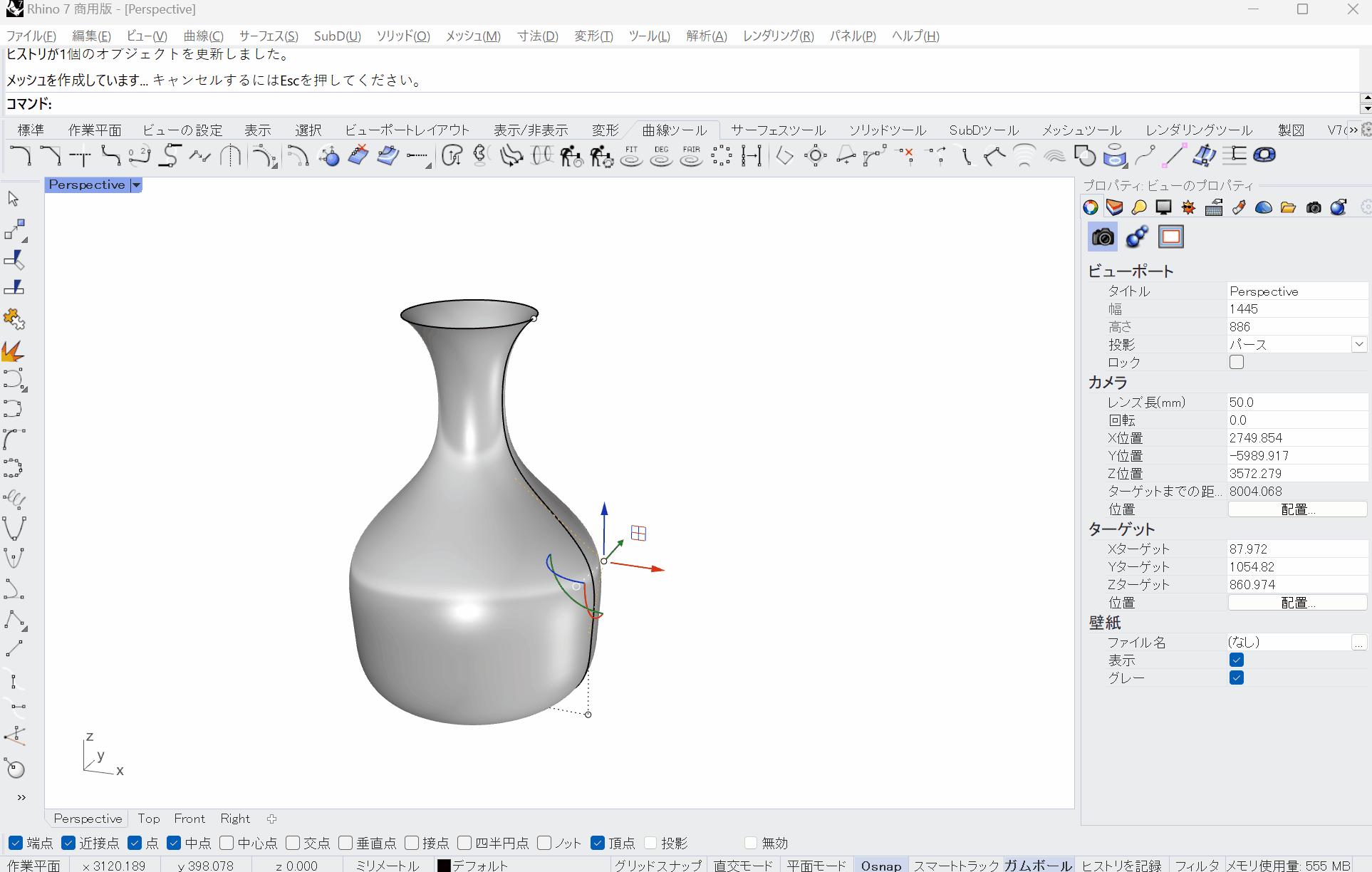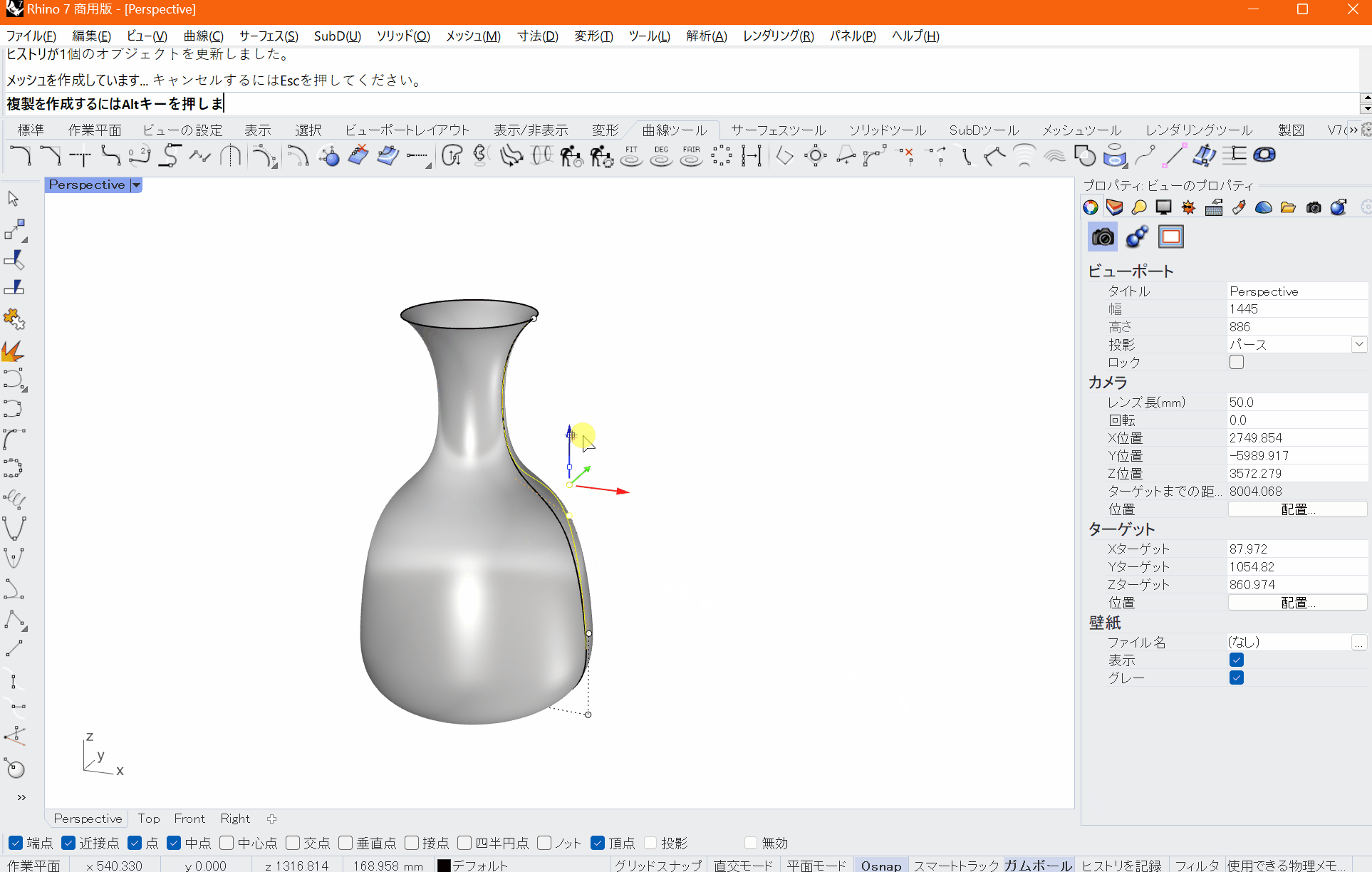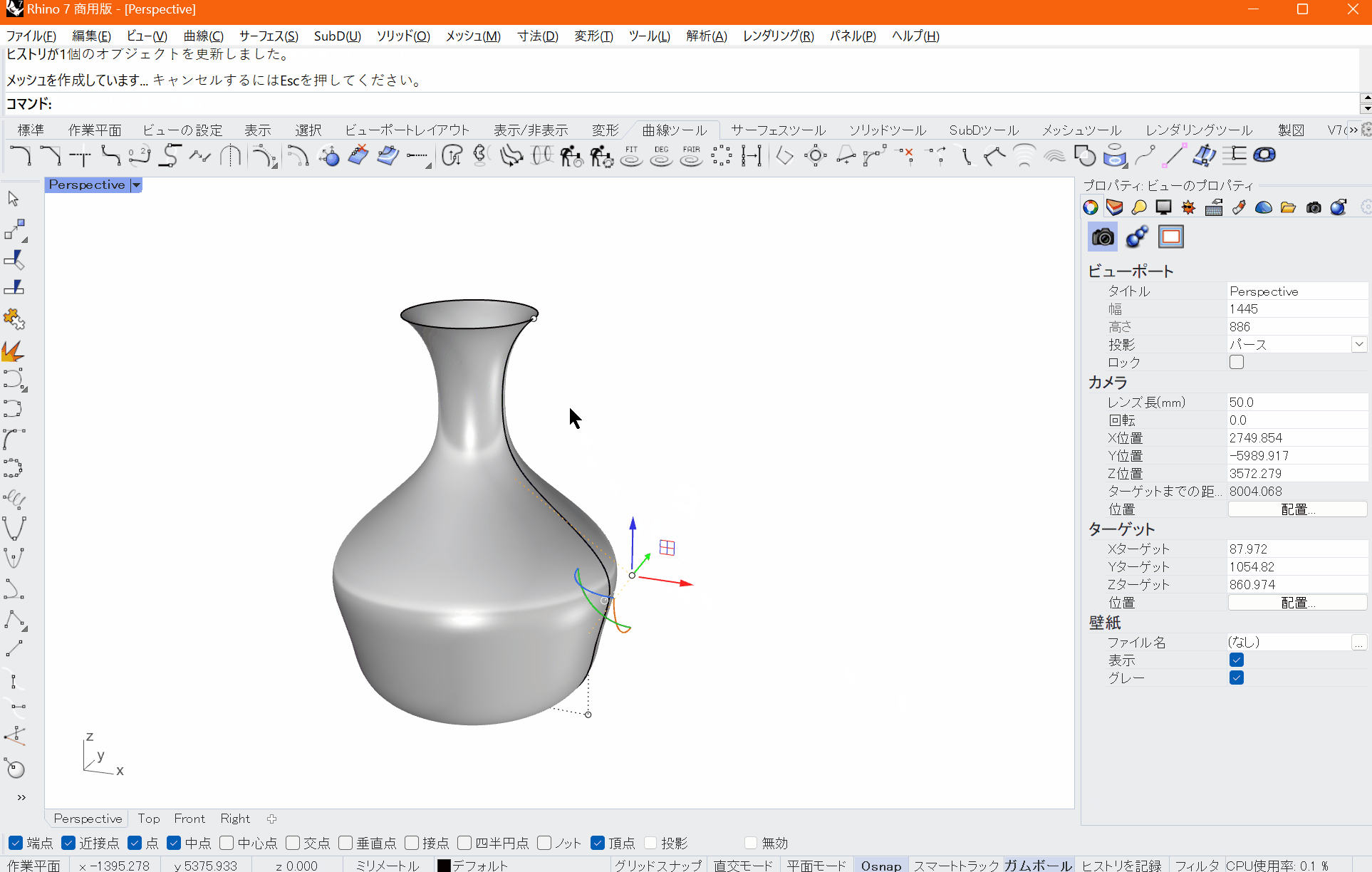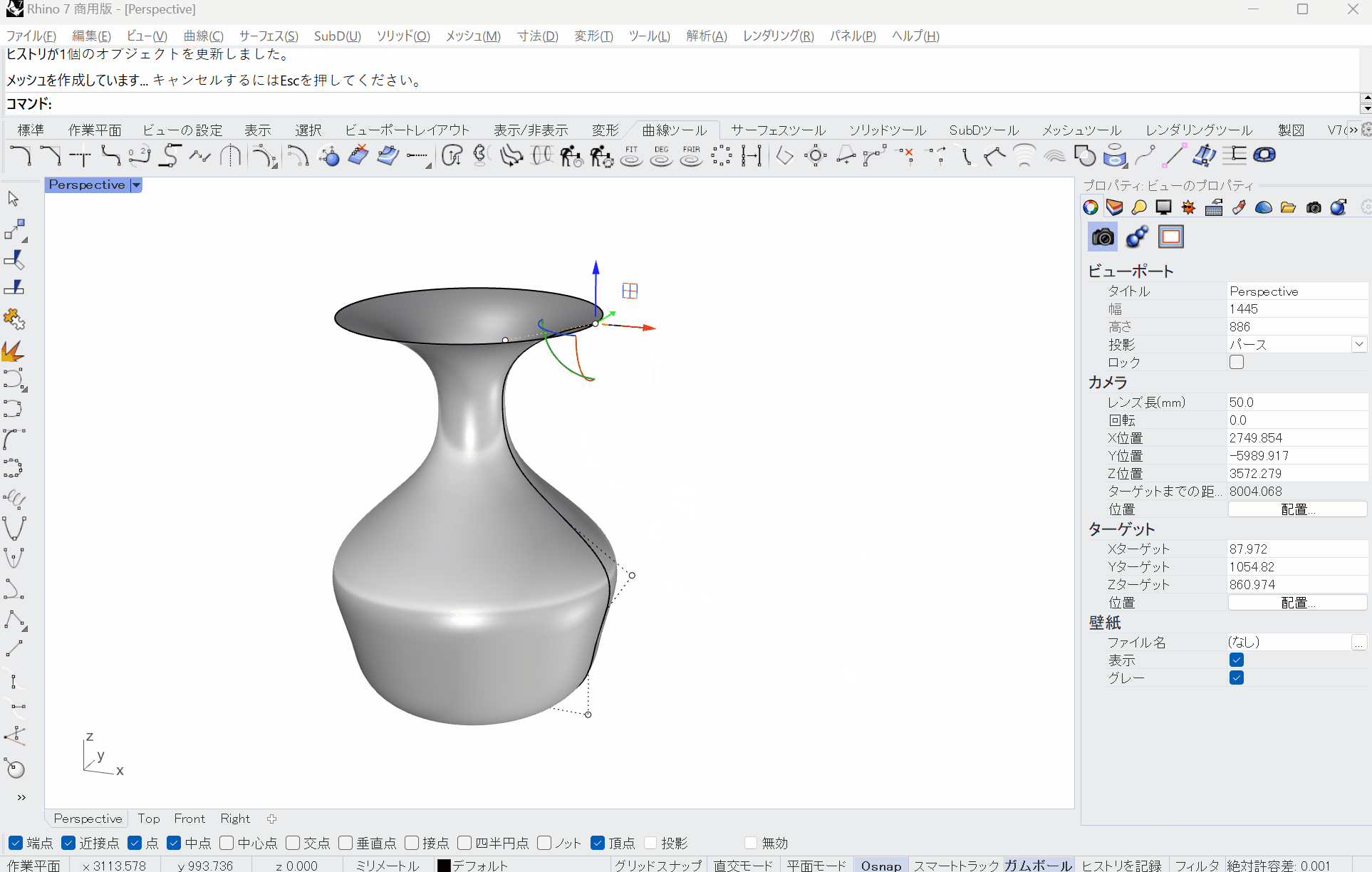
文字列でのコマンド呼び出しを用いたUI
デフォルトではウィンドウの上部にコマンド入力部があり、そちらに「Sphere」「ExtrudeCrv」などコマンドを入力することでRhinoで行えるほぼすべての機能呼び出しが可能です。GUIを通したアイコン選択でも操作可能なのですが、習熟した多くのユーザーがそうなっているようにコマンドでの操作に慣れると操作が効率化されて手放せなくなります。
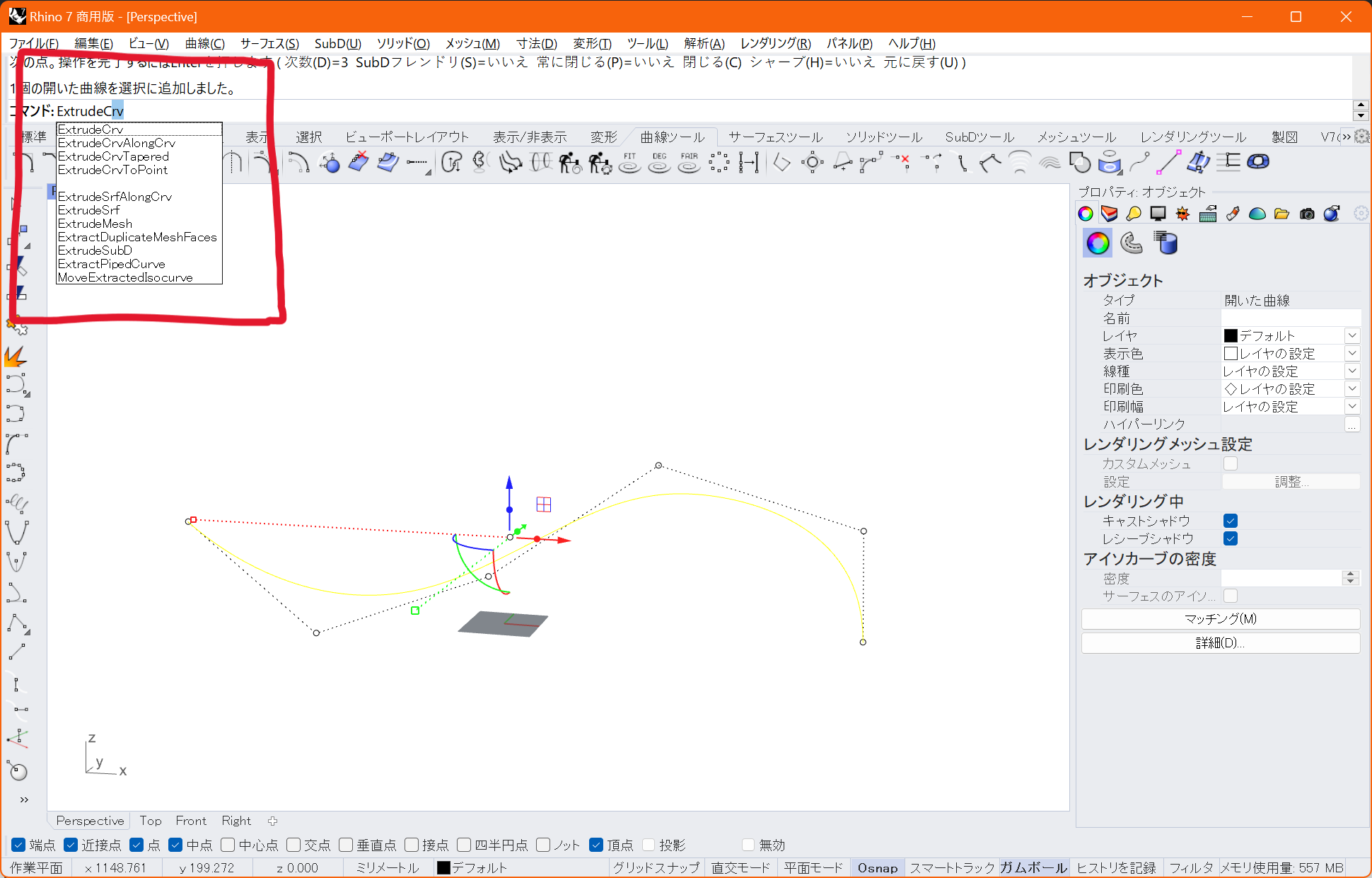
長所
高い拡張性
上述の通りデフォルトで提供されている機能は「形状の自由な編集」そのものに重きを置いている一方で、C#やpythonを通した柔軟な拡張性が担保されています。Rhinoの幾何処理やソフトウェア制御をほぼ全て利用可能なAPIであるRhinoCommonを利用した様々な拡張が容易に可能となっており、多くの業界や技術領域に特化した商用/非商用プラグインが開発されています。
C#またはpythonで容易に簡単なスクリプトやプラグインを作成できます。
他分野横断かつオープンマインドかつ活発なコミュニティ
様々な業界や研究領域、用途に対して開発された拡張機能やユーザーの知見が相互共有される独自のコミュニティが形成されており、主に公式のForumであるRhinoceros Forumsやプラグイン共有プラットフォームのFood4Rhinoを通して活発な情報交換が行われています。
短所(2023/03/24 Rhino7時点)
ノンヒストリーな思想
ほぼ全ての機械/建築用途のCADがヒストリーを基本機能としているのに対し、Rhinoはヒストリーを残さない操作が前提となっています。
正確に言うとヒストリー機能は付加的に提供されているのですが、全操作がパラメータとともにヒストリー化され修正可能となっている状態を作るのは難しく、機械設計などに比べ意匠寄りの分野で多く用いられている所以となっています。
BooleanOperationなど近似計算系処理の安定性
こちらは設定の調整やコツである程度回避できるのですが、主にジオメトリ同士の交差に関する近似処理において意図せぬ挙動をすることが多めです。
機械設計系のCADではこれら処理が非常に強力なものがあるのですが、Rhinoでは特にクセや内部処理を加味したモデリングが必要となる場面があります。
次バージョン以降で改善されるとかされないとか。。?
扱える主なジオメトリ
Rhinoでは様々な形状処理が可能ですが、意識して扱うジオメトリのデータ型自体はそれほど多くありません。
背景技術としてはNURBS(制御点グリッドと次数、ノットベクトル、重みといった情報から決定される区分多項式で表現される曲面(1次元では曲線))に理解のハードルはありますが、相当細かいことを考えない限りは特に考えなくても連続性が担保された状態で曲線や曲面を扱えます。
Point

X, Y, Zの3つの値(double)で表現される3次元空間上の点。
RhinoCommonにおいてはRhino.Geometry.Point3dという構造体で表現されており、距離の計算や加算減算、スカラー値との乗算などが定義されています。
Curve

制御点列、曲線の次数、ノットベクトルといった情報から定義される曲線。Rhinoからの利用では制御点の位置と次数あたりをコントロールすることがほとんどになります。
RhinoCommonにおいては複数のクラスが存在していますが、一般的な利用においてはこれらの違いを意識せず全て"Curve"として扱えるよう作られています。例として複数のCurveをつなげたり切り離したりしてもそれらはすべてCurve、という使い心地になっているが内部処理的には様々なクラスが利用されているといった感じです。
。
- Rhino.Geomtry.LineCurve
- Rhino.Geometry.ArcCurve
- Rhino.Geometry.PolylineCurve
- Rhino.Geometry.NurbsCurve
- Rhino.Geometry.PolyCurve
上記含む全てのCurveに対してパラメトライズがされているという点が重要で、曲線を数直線上のある閉区間と対応付けた状態になっており、閉区間内の1つのdouble値に対応付けて曲線上の1点の情報を取得することが可能です。、微分幾何における曲線の定義を見ると自然に理解ができると思います。
例として始点を0、終点を1とパラメトライズしたCurveにおいて、0~1の値をとるパラメータtを与えることで対応する点の位置、接線方向、曲率、捩率といった微分まで含めた情報を取得することが出来ます(簡単な微分幾何の勉強の道具としても楽しい!!)
また、3次元空間上のPointに対するCurve上の最近傍点の計算や曲線間の最近傍点の計算、離れた2曲線を連続性を担保して繋ぐ曲線の計算など高度かつ高速(実処理部分はC++)な処理が多く提供されています。
Surface(UntrimmedSurface)

上記Curveが1次元のNURBS曲面と見ると、こちらは2次元のNURBS曲面で、グリッド状に与えられた制御点位置や次数によって形状のコントロールが可能です。
曲線と同様の処理がパラメータu,vによって与えられており、微分情報の取得や様々な処理が可能です。
RhinoCommonにおいてはRhino.Geometry.NurbsSurfaceといったクラスで表現されており、ほかのクラスもありますが通常の利用で区別する必要はほとんどありません。
TrimmedSurface
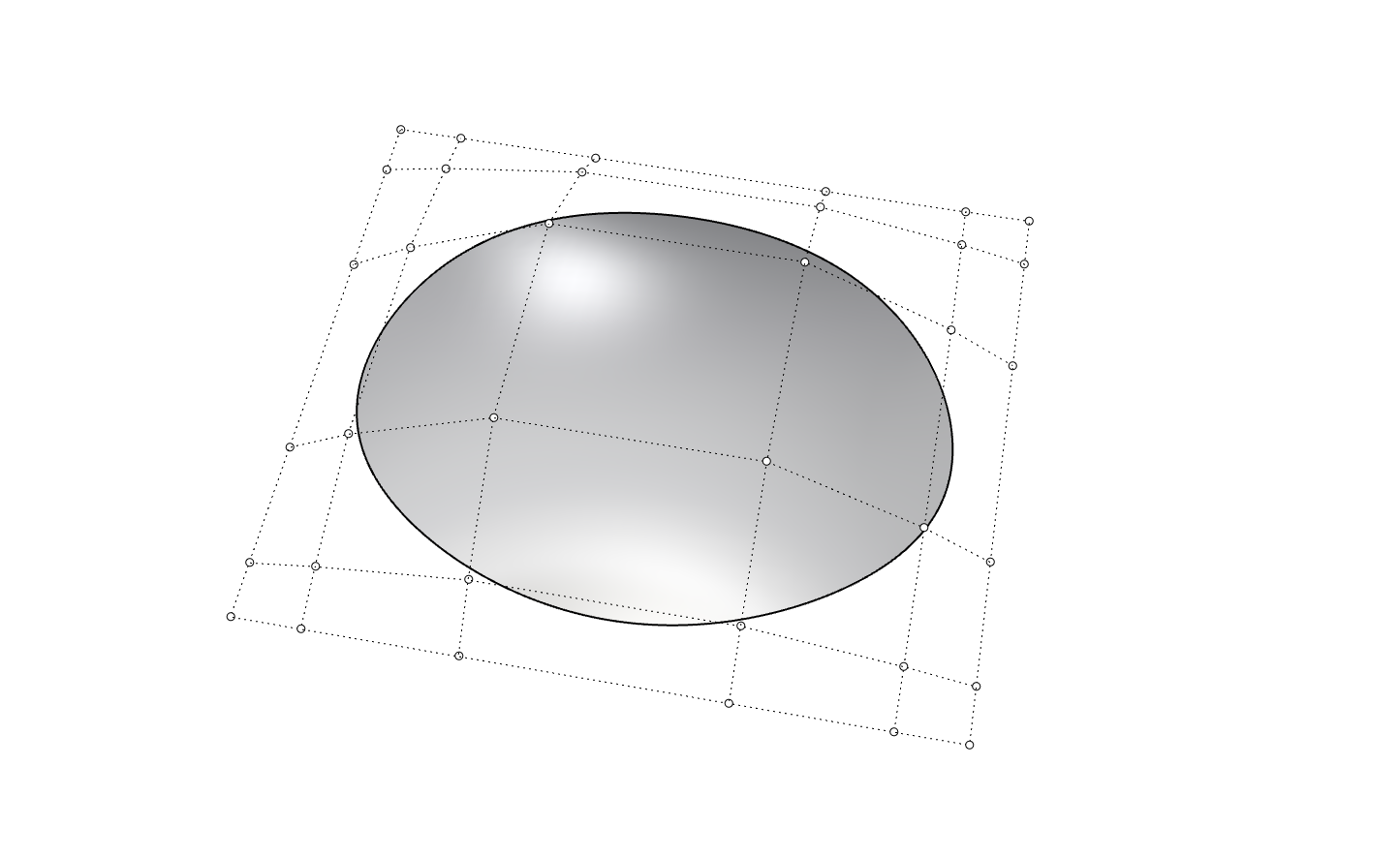
前述のSurfaceが、曲面上に乗っている(正確にはパラメトライズに対応するu,v空間上で定義されている)曲線によって切り取られているもの。輪郭形状を曲線で定義したり穴をあけたりした状態を作ったり出来ます。
内部処理では下記Brepとして扱われています。
Brep(PolySurface)
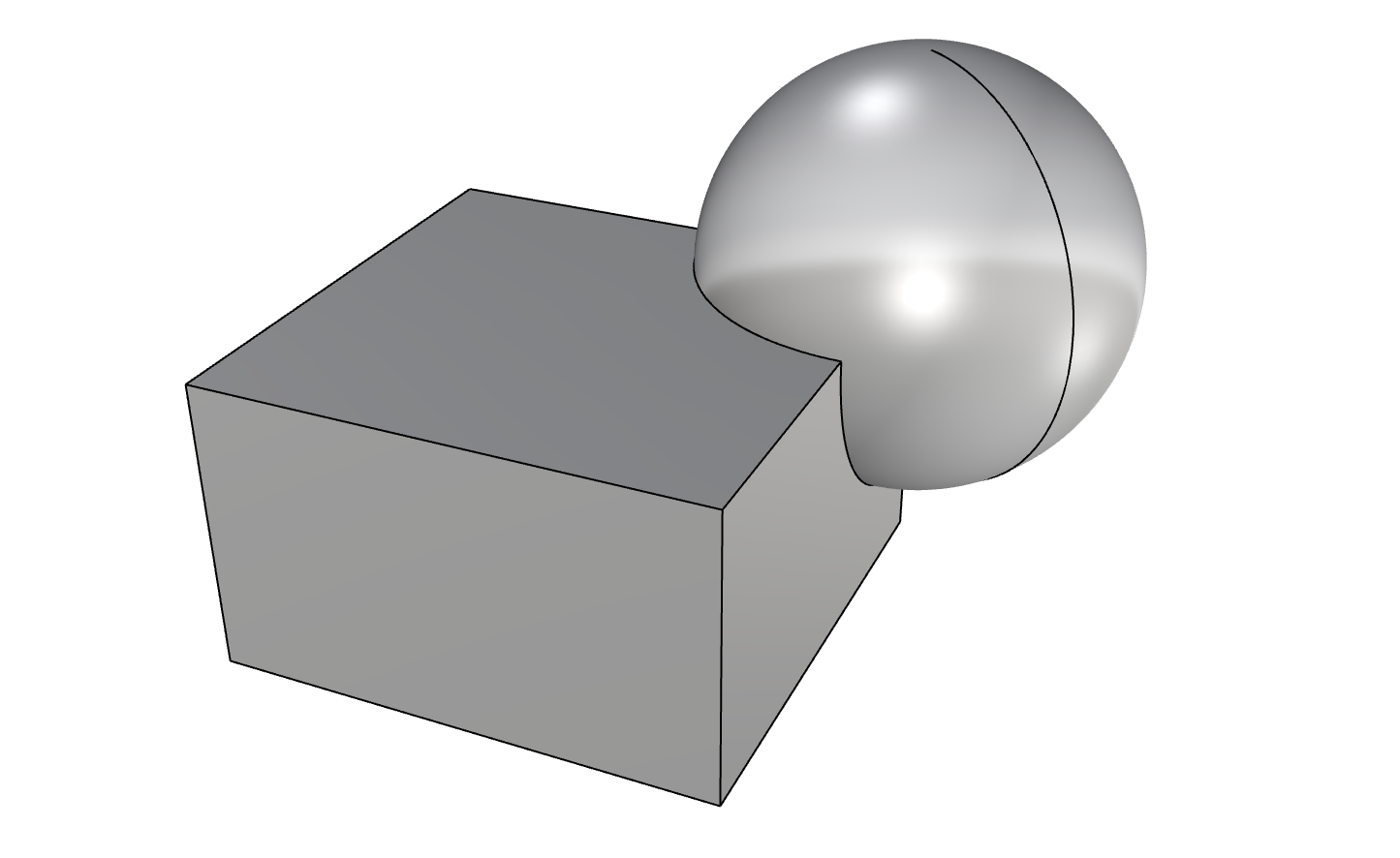
複数のSurfaceまたはTrimmedSurfaceをつなげて1体にしたジオメトリの表現。
閉じた形状を高精度かつ柔軟に定義可能であるため、多くの工業製品がBrepの恩恵を受けて設計されています(Brep自体はあらゆる3DCADで利用されている概念)。
おそらくRhinoのほとんどの用途ではこのBrepを作成してから、レンダリングやCAE・CAMでの利用、Mesh化して3Dプリントなどといった形になります。
RhinoCommonにおいてはRhino.Geometry.Brepというクラスで表現されており、下記に代表される構成要素とその接続関係から成っています。
- Vertices: 含まれる頂点となるPoint群
- Surfaces: 含まれる面のもととなっているUntrimmedSurface群
- Trims: Surfacesをトリムするためのu,v空間で表現された曲線群
- Edges: 含まれるエッジとなるCurve群
CurveやSurfaceと同様に様々な処理が提供されています。
Mesh
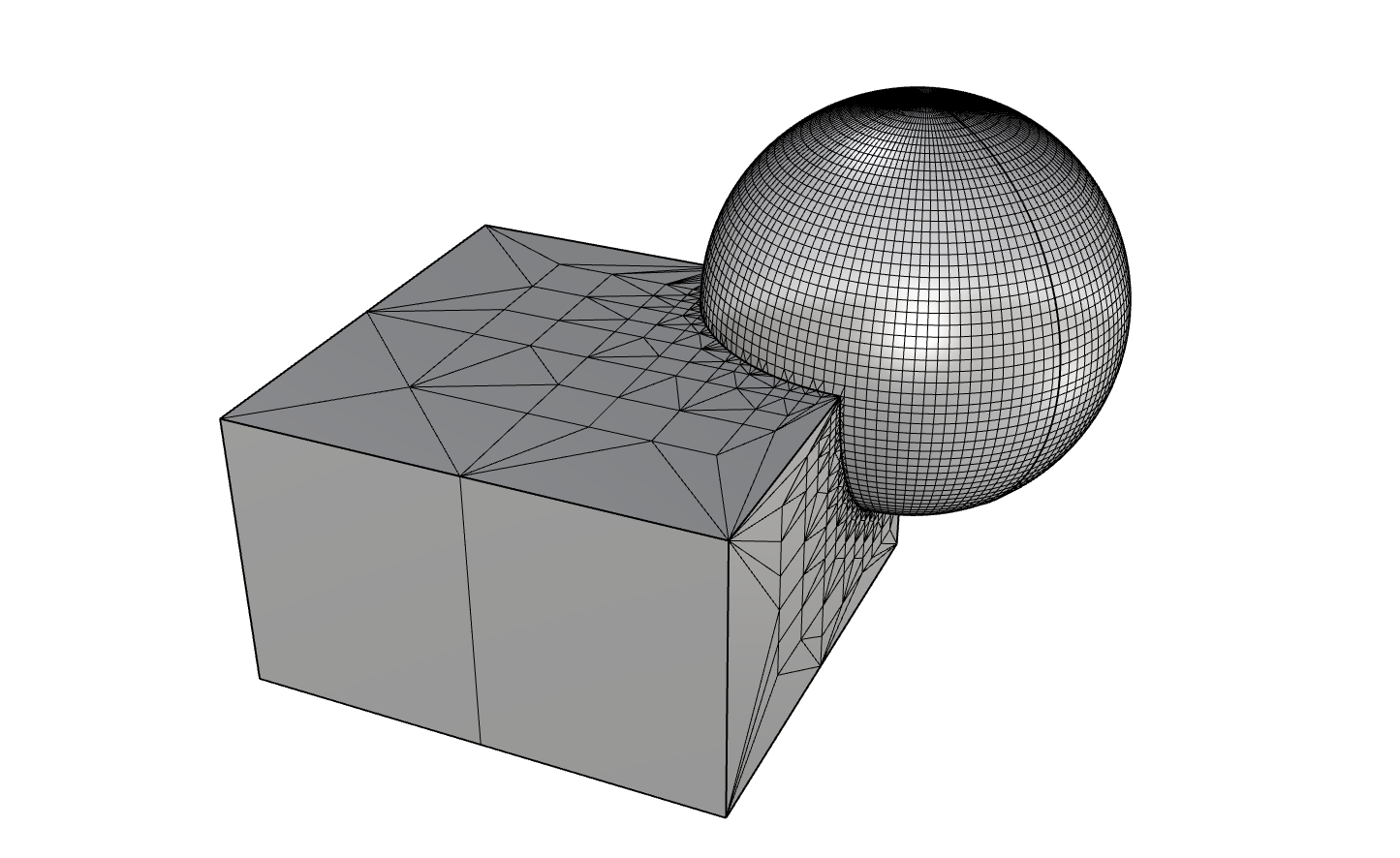
複数のPointとその接続関係で定義されるFaceから成る、いわゆるポリゴンの表現。
RhinoCommonにおいてはRhino.Geometry.Meshクラスで表現されます。
他ジオメトリと同様に最近傍点を取る処理などが提供されているだけでなく、接続情報を必要とする操作のためにTopologyVerticesやTopologyEdgesといったプロパティが提供されています。
Rhinoで直接Meshを編集していくことはほとんど無いと思いますが、レンダリングや3Dプリントなど必要となる用途は多くあります。
SubD
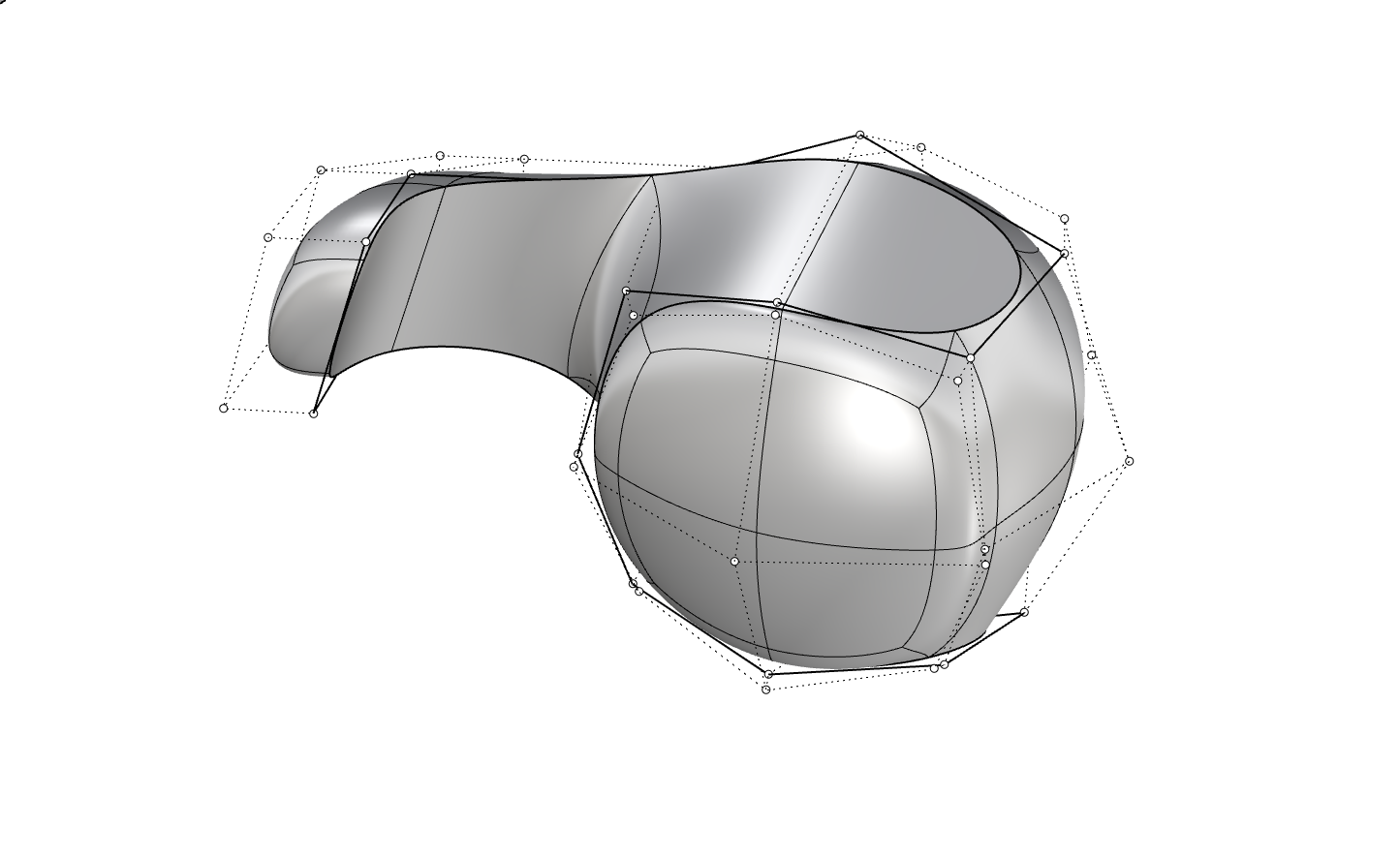
Rhino7から追加された新ジオメトリで、連続性の担保された複雑な形状を簡便な操作で粘土細工のように編集できることを指向されているもののようです。
TSpline(制御点がグリッド以外のトポロジーを持てるよう表現が一般化されたNURBSのようなもの)がかつてTSpline社によって開発されておりRhinoにもプラグインが提供されていた時期があったのですが、現在はTSpline社がAutodesk社に買収されたことによりRhinoからは利用できなくなっていたものの代替として実装されたと思われます。
技術的には、その名の通りサブディビジョンサーフェスの技術を基盤としながら、NURBSとの互換性をある範囲で実現し相互変換を実現しているようです。Brep化したあとの近似計算系処理において失敗が多い、SubDの面トポロジーによってはNURBS化時に不連続性が出るなど用途は現状限られる印象ですが、特にコンセプト段階で審美性の求められるモデリングの道具として非常に強力かつ魅力的です。
また、Brepでの表現に限界のある曲面(シャープなエッジが徐々に滑らかになるなど)が容易に実現できる点も非常に面白いです。
CG用途のサブディビジョン系のモデリングに親しみのある方ならより触りやすいかと思います。
おすすめのRhino学習コンテンツ
UIの見方から基本操作まで、ゼロからの入門に良いです
自分が悩むことは大抵ここで一度は質問されています。英語で質問すれば強い方や開発者から即答されたりします
Rhino周りの開発について、基礎から発展まで膨大なコンテンツがあります。
開発で困ったらここ読み込むのが何だかんだ良いです
pythonでのRhino開発について詳細に解説されています
短い動画や教育コンテンツがそろっています
さいごに
本章では、Grasshopper周りの開発のために前提知識として有用と思われるトピックに触れながらRhinoについて概説を行いました。
次章ではGrasshopperについての概説から内部処理の仕組みなどを書き、プラグイン開発などについて進んでいければと思います。