はじめに
あけましておめでとうございます。昨年のNature Architectsではちょっとしたパズルブームが起こりました。この記事では、特に人気が高かった木組みパズルと箱詰めパズルの2種を取り上げ、3DCAD・3Dプリンタ・最適化ソルバなどを利用した様々なアプローチでパズルに取り組んだ様子を紹介します。
学生時代に友人から借りた木組みパズル。目的は3つのピースを組んだ状態にすること。10年間解けていない。
2024年最も人気を博したパズル。箱にいれるというシンプルな目標ながら、なかなかの難易度。
ルービックキューブに代表される twisty puzzle。近年の競技用パズルの滑らかさについては過去記事 で紹介。
折り紙パズル。目的は、折りたたむことで片面は白、もう片面は黒しか見えない状態にすること（左下）。弊社CEOには楽勝だったよう。
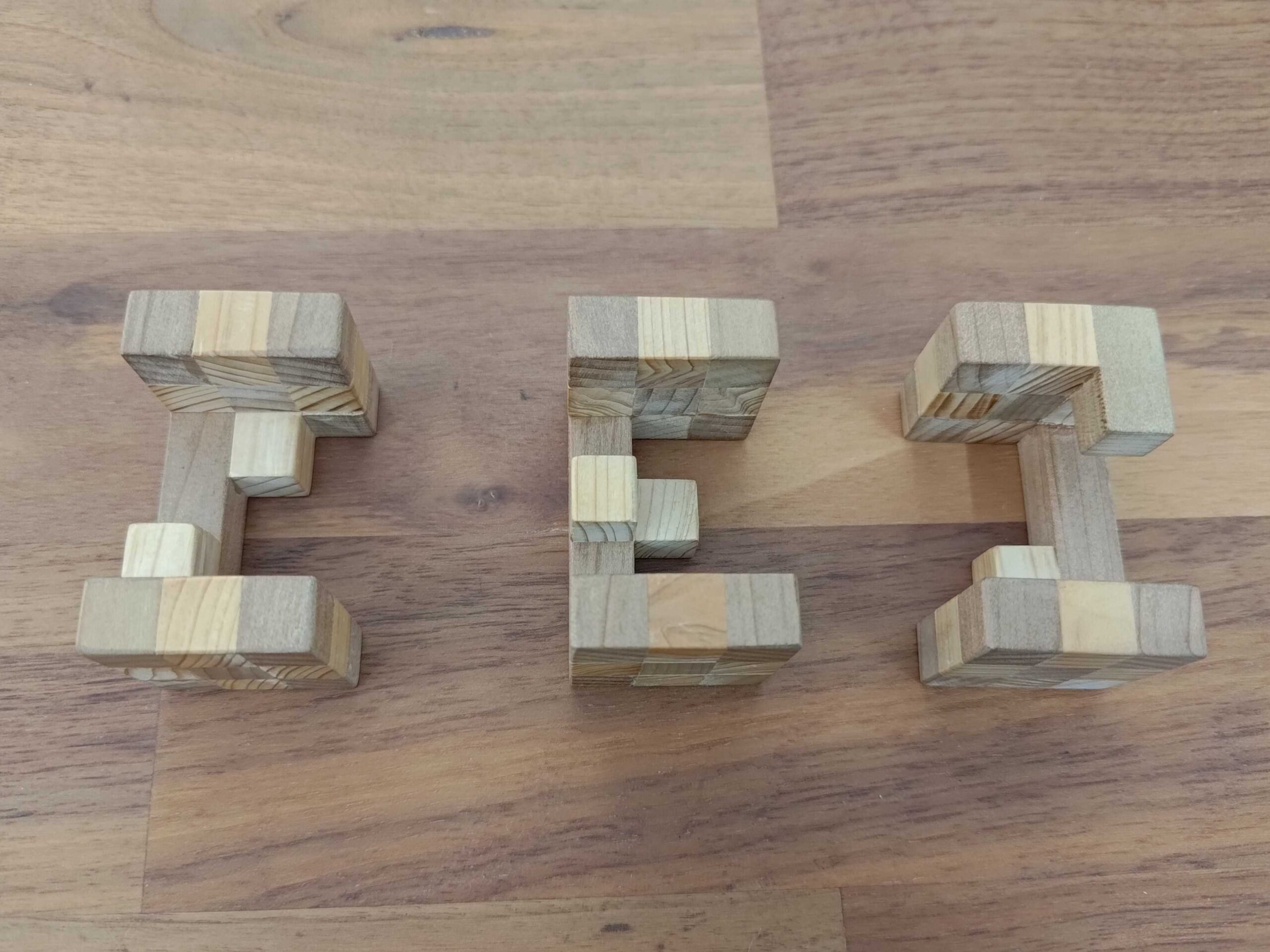
木組みパズル
パズルブームの発端は一つの木組みのパズルでした。私が学生の時（10年ほど前）友人から借りて、解けたら返却予定でしたが未だに手元にあります。弊社はパズルが好きな人が多いので、オフィスのサンプル置き場に設置してみました。
3つのピース
パズルの目的
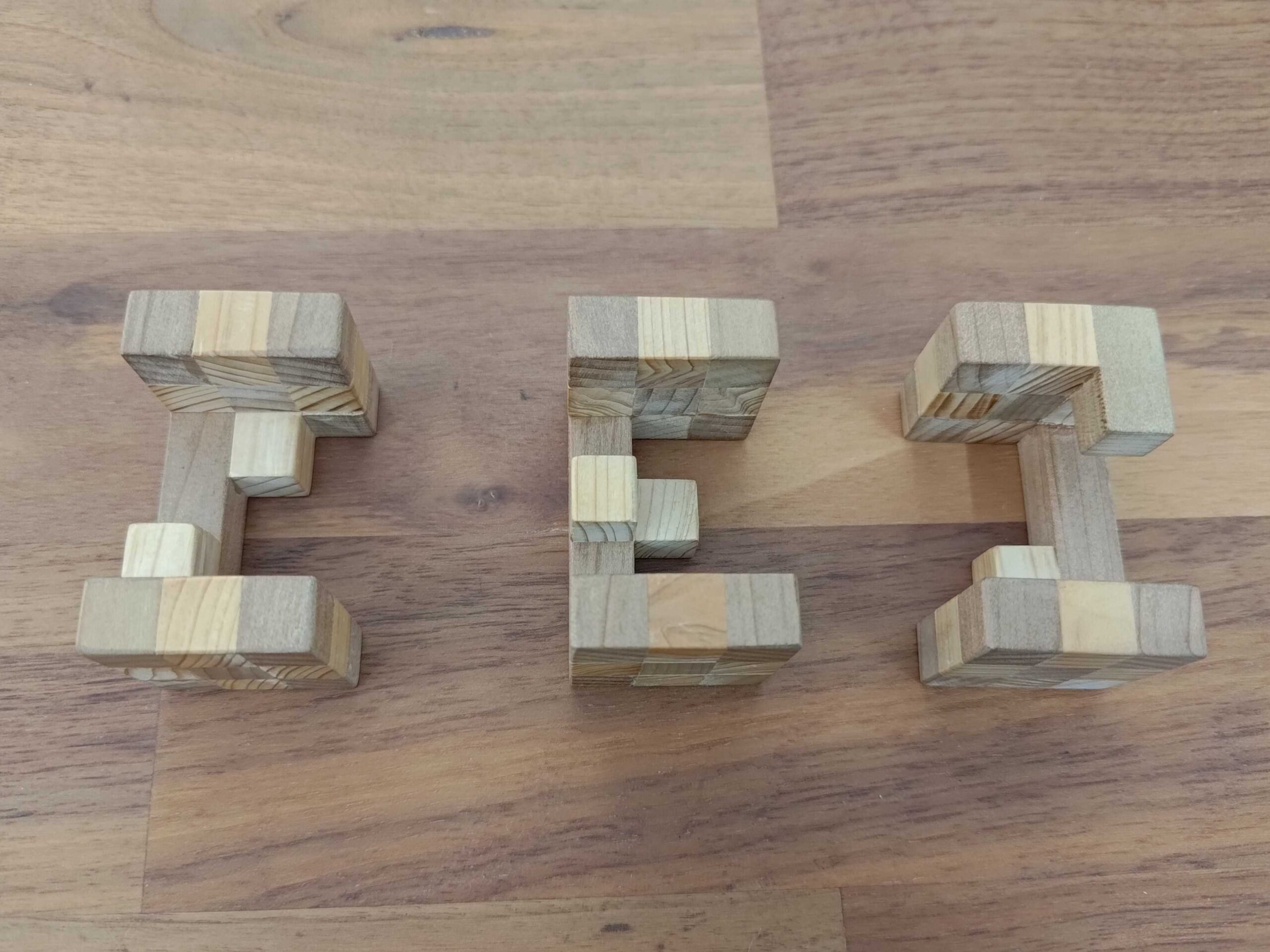
計算機で並進総当たり
設置後、何人かが手でパズルに取り組みましたが、すぐには解けません。まもなくチーフエンジニアにより3Dデータが作成・共有されました。これにより計算機でパズルに取り組むことが可能となりました。
3Dデータを作成
パズルを解くためにとった方法は以下です。本来のパズルの楽しみ方ではなくずるい感じもしますが、10年解けてないので手段を選んでいられません。
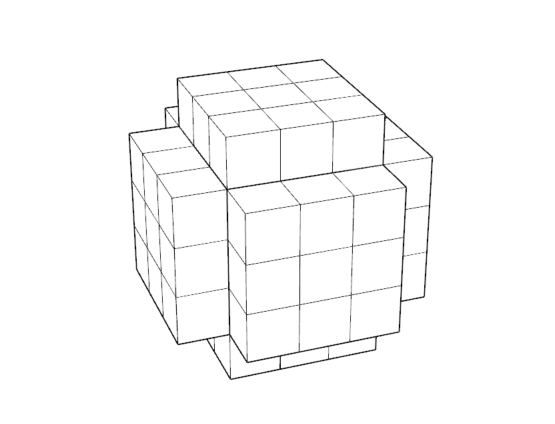
組み立て状態（完成状態）を求める
組立状態から干渉無しで可能な操作で到達できる状態を列挙
分解状態まで到達する操作が見つかったら、それを逆順にすることで組み立て手順を得る
上記手順の結果、2つの完成状態と、そこから遷移可能な4状態が発見されました。しかしながら、分解状態までは到達することができず、並進のみの操作によっては解けないことが明らかになりました。
完成状態とそこから各手数で遷移可能な状態。干渉は各立方体の中心点の重なりで判定。
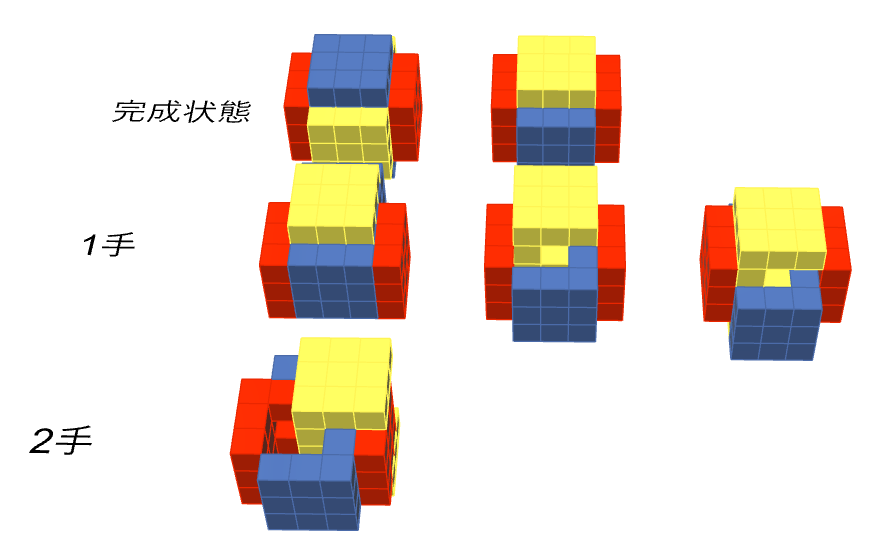
インターロッキングパズル
エンジニアの一人から、類似のパズルを生成するアルゴリズムに関するの論文[1] を教えてもらいました。
それによると、今回取り組んでいる木組みのパズルは、業界ではインターロッキングパズルと呼ばれいていて、1つ目の部品が外れるまでの手数をパズルのレベルと呼ぶようです。
インターロッキングパズルを解く手順を見つけることはNP困難に属する問題であり、ブロックの数が増えると組み合わせが爆発的大きくなりますが、今回のサイズにおいては簡単に列挙可能でした。
文献では任意のレベルのパズルを効率的に生成する方法が紹介されていて、ソフトウェアも公開されていました。せっかくなので、6手で外れる弊社ロゴマークのパズルを生成してみました（冒頭カバー画像）。
パズル生成アルゴリズムによって得られたN形状。これの外形を削ってカバー画像のパズルを作成。
上記文献においても、パズルの操作としては並進のみが扱われていました。回転を考慮した研究もなくはないようですが、干渉の判定のの計算が難しくなるため、計算機で扱うことが非常に困難と予想されました。
3Dプリンタの利用
さて先程の木組みパズルですが、回転の操作の考慮は計算機では困難と判断し、完成状態を3Dプリントして外す方法を探りました。
造形品を動かすことで、先程列挙した状態に加え、回転動作で到達できる状態がいくつか発見されましたが、残念ながらこの方法でも解は見つかりませんでした。
クリアランスと造形の角度をうまく調整することで一般的なFDMのプリンタでの造形が可能。
造形された完成状態の候補2種。
本当に解はある？
あまりの困難さに、貸してくれた方に連絡してみたところ、
「父が趣味で作ったもので、もしかしたら設計が間違っているかも。しかし、一度解けたことがあるような気がする。」とのこと。
設計が間違っているか、あるいは残る可能性としては回転を含む動きで試せていないものがあるかいずれかです。後者がない可能性を証明することは困難ですが、前者の可能性が高いのではというのが現時点での認識です。
後日わかったのですが、以下のサイトに良く似たパズルがあるので、これを元にした可能性が高いです。サイトに記載のパズルは回転を使うととけるよう巧妙に設計されていました。
https://puzzlewillbeplayed.com/555Cross/Okey3PieceBurr/
結論として解けてないのは残念ですが、奥深いインターロッキングパズルの世界に触れることができ、かなり楽しむことができました。
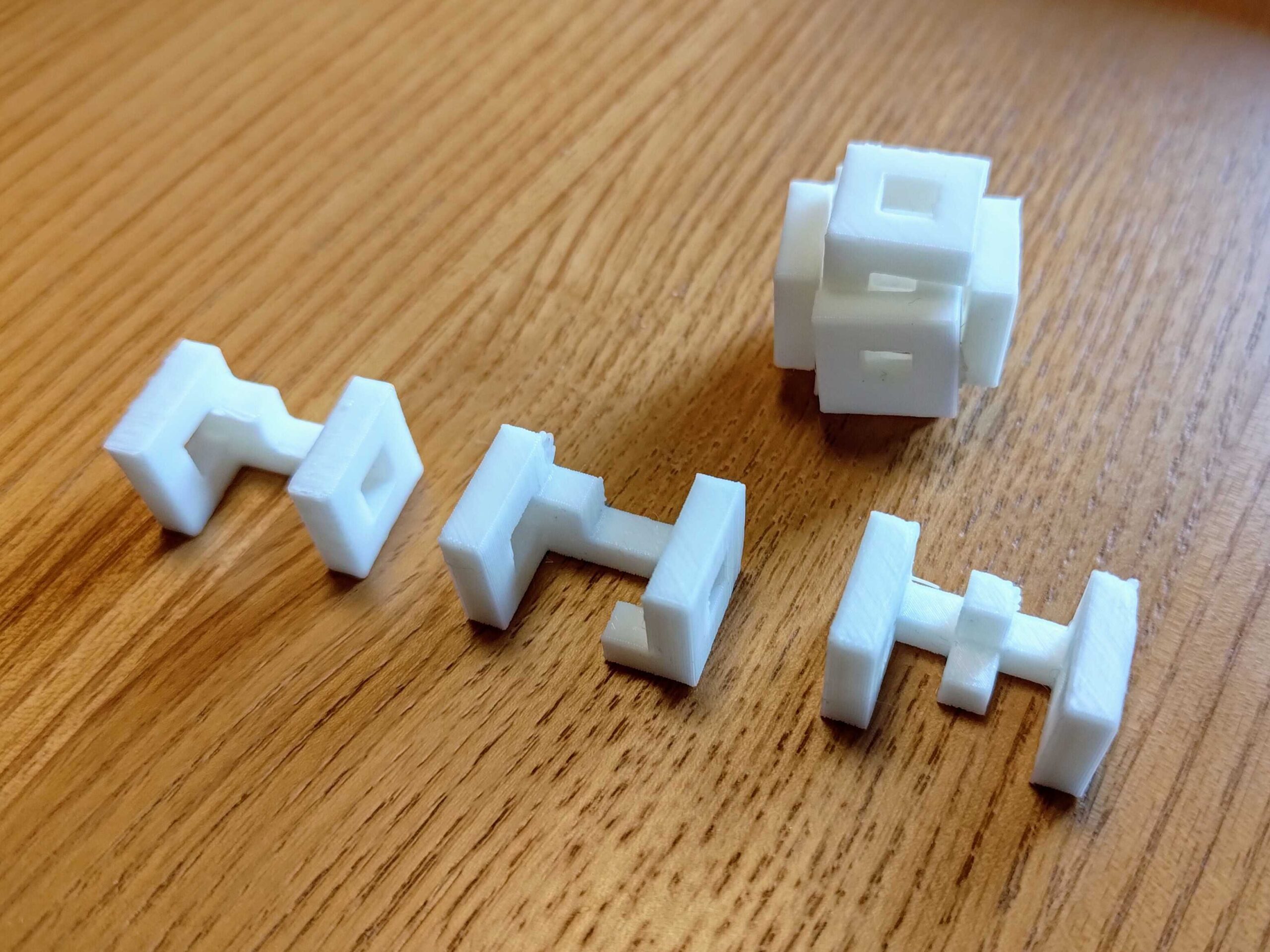
おそらくこれがオリジナルか。Design and Copyright : 山本長徳 (Osanori Yamamoto) (2008) .
[2]
箱詰めパズル
プラパズルNo.24 （発売年1963～？）
[3]
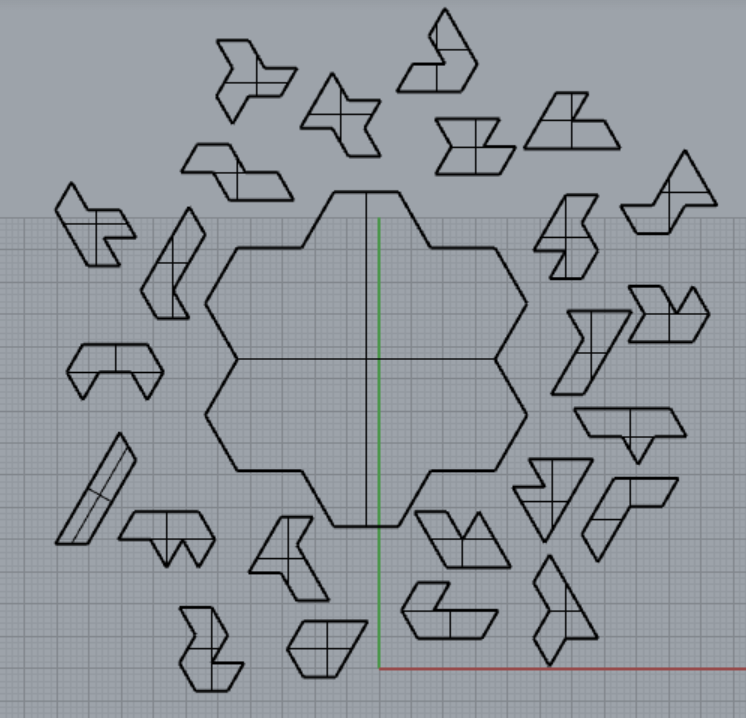
2024年社内で最も流行ったパズルは間違いなくこれでしょう。パズルの目的は24個のピースを箱に詰めることです。
弊社CTOが骨董市で購入したそうで、フタに書かれた文字のフォントが時代を感じさせます。電子計算機と結びついているそうなので、計算機との共創を掲げる弊社としては取り組まざるを得ません。
正三角形を連結してできる図形はポリイアモンドとよばれます[4] 。7枚のポリイアモンド（ヘプタモンド）には24種類ありますが、そのすべてを一枚ずつ使っているところがこのパズルの美しいところです。
何人か挑戦しましたが、人間で解けたのはエンジニアYさんのみ（ブログ公開時点）。残り2~3まで詰めた後、部品を入れ替えながら解を探っていく手法のようです。
計算機で解く
計算機で解いてみます。こちらもチーフエンジニアにより即座に3Dモデルが作られました。
３Dデータを作成
はじめ、何人かのエンジニアが本業でよく使用するCAD環境のRhinoceros/Grasshopper ＋ 最適化ツールtunnyを使って解こうと試みましたが、困難でした。そもそもtunnyで使用できるのは関数の性質がわかっていない場合に用いられるブラックボックス最適化であり、今回のような中身のわかっている問題については、もっと適した手法がありそうです。
文献[5] によると、パズル用のソルバとしてはburrtoolsがよく用いられるが、このような問題に対しては整数計画法向けの汎用ソルバのほうが高速とのことです。今回はオープンソースの混合整数計画問題向けのツールであるPython-MIP[7] を用いることにします。
先程の文献を参考に、以下のように定式化しました。各ピースの形状が異なる点が文献とは異なるので、制約2を追加しています。
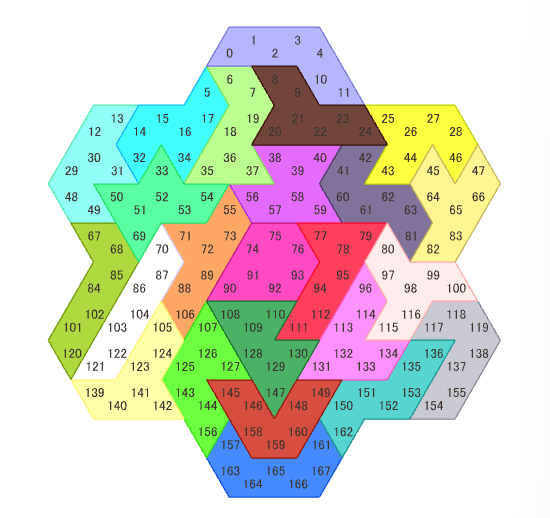
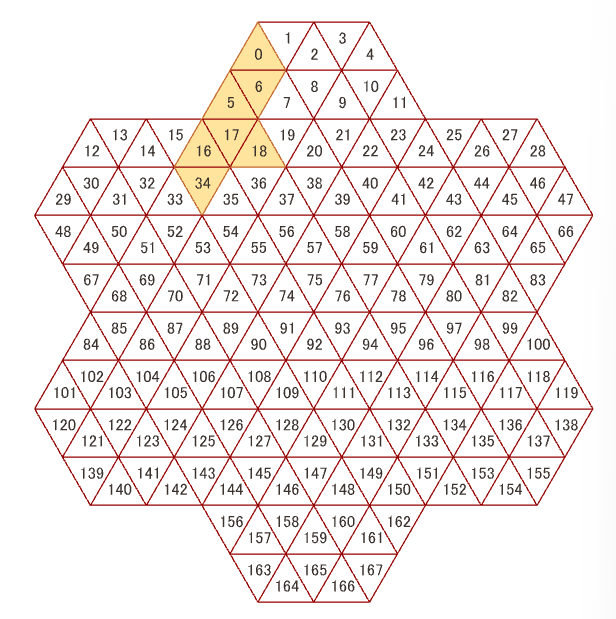
箱形状を構成する各正三角形に番号をふる 0 ～ 167 （下の図）
変数
部品iの可能な置き方を、盤面の番号を用いた2値変数 p_i(a,b,c,d,e,f,g)で表す
（ただし表現を一意にするために a < b < c < d < e < f < g ）。
変数の値が1であれば部品が配置され、0であれば配置されていないことを表す。
例えば部品0が（下の図の黄色）のように置かれているとき、p_0(0,5,6,16,17,18,34)=1となる。
変数の数は全部品の全配置方法の数となる。全13667個。
下記を満たすことがパズルの解の必要十分条件
制約条件1：（すべての場所ちょうど1枚のピースが覆う）
場所0に関する制約式:
(場所0を埋めるすべての置き方に対応した変数の和） = 1
つまり、p_0(0,5,6,16,17,18,34) + p_0(0,6,7,18,19,20,38) +… =1
場所1に関する制約式:
(場所1を埋めるすべての置き方に対応した変数の和） = 1
……
制約条件2：(すべての部品を1度ずつ使用)
部品0に関する制約式:
(部品0のすべての置き方に対応した変数の和) = 1
つまり、p_0(0,5,6,16,17,18,34) + p_0(0,6,7,18,19,20,38) +… =1
部品1に関する制約式：
(部品1のすべての置き方に対応した変数の和) = 1
……
p_1(0,5,6,16,17,18,34)=1のピース配置。
実装は、Rhino/Grasshopper上で形状を元にソルバに与える情報を準備し、pythonコンポーネント上で解いた後、Rhino/Grasshopperで可視化する構成としました。
Grasshopper上での構成
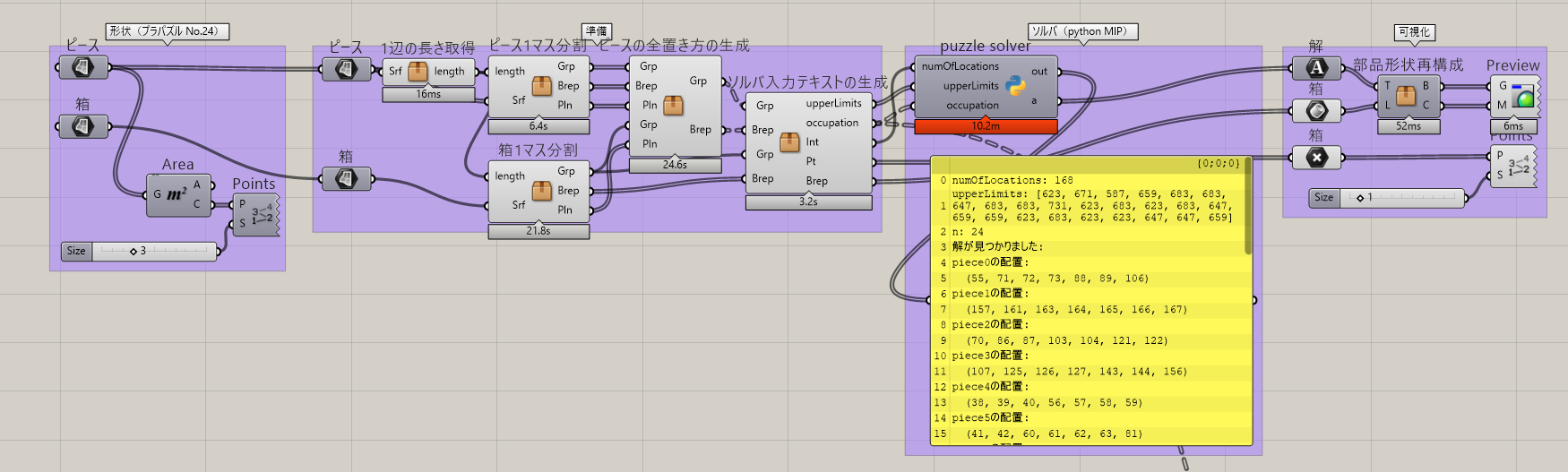
実行した結果、ラップトップPCで10分程度で解を得ることができました。
⚠ ボタンを押すとパズルの解答が表示されます
見つかった解の一つ
今回、変数が13667個あるので、総当たりだと2^13667=1.50297×10^4114 通りとなり現実的ではないですが、python-MIPで使用されるCBCと呼ばれるアルゴリズムが非常に優秀で解を発見できていることは興味深いです。
また、実行速度から想像するに、人間はさらに効率の良いアルゴリズムで解いていることが予想され、計算機上での探索は改良の余地がありそうです。
さいごに
私は普段非線形性の高い解析をやることが多く、最適化ではブラックボックス最適化を使いがちだったので、問題によって正しく使い分ける重要性を再認識でき、非常に勉強になりました。
今後も、おもしろいパズルがあれば手と計算機で味わっていきたいと思います。
参考文献
[1] Rulin Chen and Ziqi Wang and Peng Song and Bernd Bickel. "Computational Design of High-level Interlocking Puzzles". ACM Transactions on Graphics (SIGGRAPH). 2022. https://sutd-cgl.github.io/supp/Publication/projects/2022-SIGGRAPH-High-LevelPuzzle/index.html
[2] puzzlewillbeplayed.com. "Okey 3 Piece Burr". https://puzzlewillbeplayed.com/555Cross/Okey3PieceBurr/ . (2025/01/17閲覧)
[3] 株式会社テンヨー. "テンヨーの歩み". https://tenyo.jp/history.html . (2025/01/17閲覧)
[4] ウィキペディア. "ポリイアモンド". https://ja.wikipedia.org/wiki/%E3%83%9D%E3%83%AA%E3%82%A4%E3%82%A2%E3%83%A2%E3%83%B3%E3%83%89 . （2025/01/17閲覧）
[5] Mutsunori Banbara, Kenji Hashimoto, Takashi Horiyama, Shin-ichi Minato,
Kakeru Nakamura, Masaaki Nishino, Masahiko Sakai, Ryuhei Uehara,
Yushi Uno, Norihito Yasuda, "レプ・タイルの定式化を用いた各種ソルバの性能比較", 工知能基本問題研究会 SIG-FPAI-119-01, 2022, https://www.jstage.jst.go.jp/article/jsaifpai/119/0/119_02/_pdf
[6] @miso_taku, "Python mipライブラリを使った数理最適化", https://qiita.com/miso_taku/items/be16af812f3d81486bd4 , (2025/01/17閲覧)
[7] Python-MIP, https://www.python-mip.com/ , (2025/01/17閲覧)
