前書き

企業における解析技術者の重要な業務の一つはシミュレーションを実行しないことです。 一体何を言っているのだ、と思われるでしょうが、非常に重要な役目の一つだと私は考えています。

昨今は汎用解析ソフトの普及や解析リソースの潤沢化によって、何らかの課題に直面したエンジニアが、「とりあえず数値解析しておくか」と軽いノリで実行するきらいがあります。もちろん最近のソフトは優秀であることから相応のインプットを与えればそれなりの答えが返ってきますが、その答えで必要十分に課題解決可能か？という点を本来は慎重に検討しなければなりません。

なぜならば、結局のところ解析にもコストがかかるからです。 営利企業である以上は同程度の成果を得られるのであれば、最も低コストで課題を解決できることが正であり、数値解析が本当にその一手なのかを慎重に見極める必要があります。

シミュレーションは前述の通り以前に較べればその負荷は軽くなりましたが、例えば試作実験であれば(材料は限定されますが)3Dプリンタの普及による一点モノ製作コストの低下もある等、他手法も日進月歩な為、検証したい事柄毎に適宜ベストな課題解決選択肢を提案できるようにすることが解析技術者のあるべき姿でしょう。

さて、一つ数値解析が本当に必要かどうかを判定する手段として"理論値や公称値で大まかな値を出して相場感を把握する"方法が考えられます(オシャレな言い方をするならば「フェルミ推定」？)。 むろん遥か昔から行われている方法ではありますが、ある程度の数値を見積もってそれで十分と判断できる場合はシミュレーションを実行しないで良しとする判断材料に使えることから、決して過去のものとして忘れさってよいプロセスではないはずでしょう。

実際にやってみる:EVの航続距離

一例としてテスラ社の2023 Model S Baseの航続距離をインターネット上にある公開されているデータから導出してみることにします。もちろん公式HPに実測値が載っていますが、今回は理論的推論からどれだけその値に迫れるかの検証を行うことになります。尚以下記事内リンクは参考文献に飛びます。

自動車の航続距離(給油・充電をせずに移動できる距離)は次の式で求められるとします。

航続距離=(自動車の移動に使用できるエネルギー)/(一定距離移動する際に消費するエネルギー) ・・・①

分子、分母をそれぞれ求めてみましょう。

まず分母に関してです。

一般に自動車はドライブ中に大きく分けて4種の抵抗を受けていると考えられます。

• 転がり抵抗
• 空気抵抗
• 加速抵抗
• 勾配抵抗

詳細を見ていきましょう。

1.転がり抵抗

タイヤが回転する際に摩擦やタイヤの変形等によって発生する抗力。

F1=転がり抵抗係数(RCC)×車重(w)×重力加速度(g) ・・・②

で定義されます。

重力は一般的に使用される値(9.8m/s2)とし、それ以外の未知数の調査を行いましょう。

転がり抵抗係数は標準的なタイヤの値0.005とします。

また、車重は公式HPの情報から2190 kgとあります。余談ですがEVはバッテリ積載分同格のガソリン車と較べると約500~ kg程重めになる傾向があります。

ここに、ドライバーや諸々の荷物による100 kgを追加すると、

F1=0.005×(2190+100)×9.8=112.2 [N]

となります。

2.空気抵抗

車体が移動する時に空気から生じる抗力。

F2=0.5×空気抵抗係数(Cd)×前方投影面積(A)×空気密度(ρ)×速度(v)^2 ・・・③

で定義されています。こちらも同じく値を調べていきましょう。

空気抵抗係数は公式HPに0.208とあります。2024年現在において乗用車のトップクラス水準が0.2代前半であり、本車両もその範囲にあると言えるでしょう。

前方投影面積は自動車をフロントから見た時の面積になります。こちらは大まかな寸法として、公式HPに全高(1.445 m)と全幅(1.964 m)が出ていますのでこの値の長方形を面積とします。(実形状は台形に近いことからもう少し小さくなります。)

空気密度は理科年表より20 ℃の時の密度1.2 kg/m3とします。

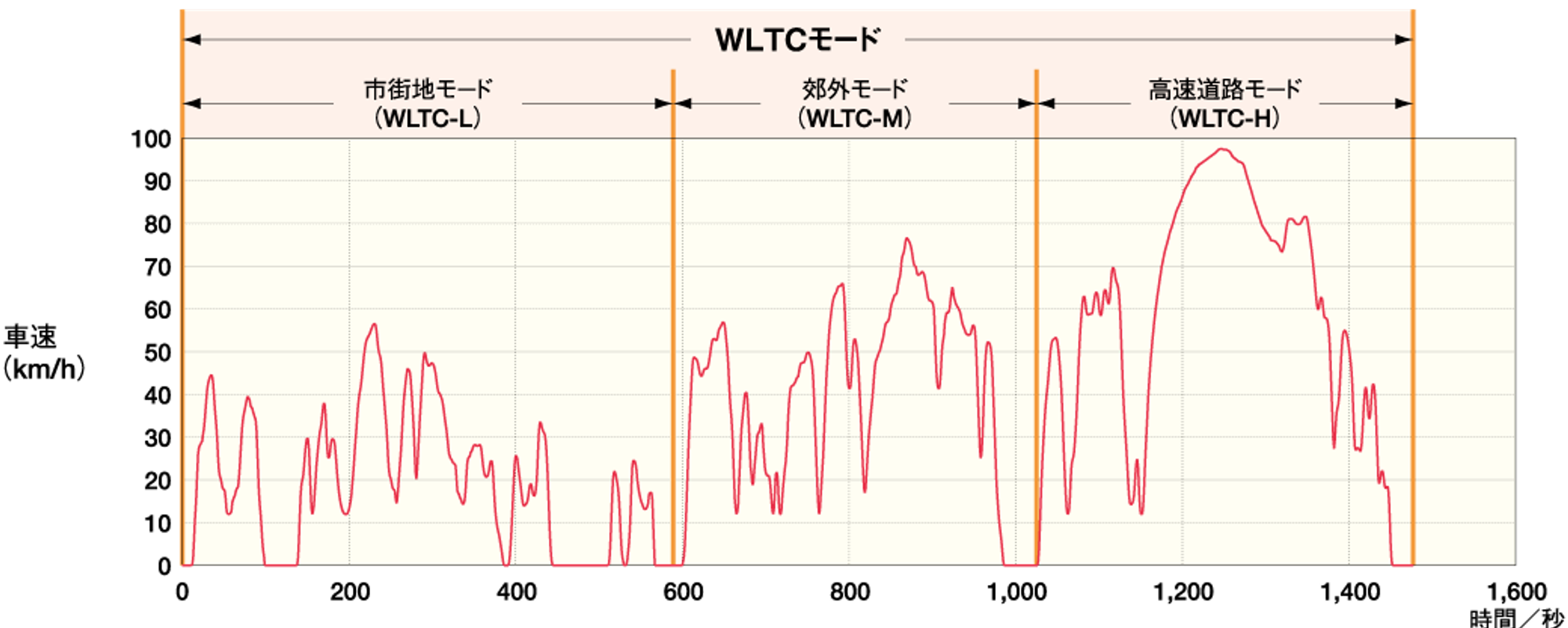
速度は使用状況によって変わりますが、今回は2024年現在で燃電費を測定する際の国際基準であるWorldwide harmonized Light duty Test Cycle(WLTC)モードを参照します。

WLTCモードは国際的に決められた”走り方”であり、現在一般に掲載される燃電費は各車このモードに従って走らせた時の消費量から算出されています。 日本自動車工業会 様HPから抜粋

加減速によって実際の利用状況に近い走行が行われるとされています。ただし、今回は概算ですので全モードの平均値36.6 km/h(10.17 m/s)で代表することにします。

以上より、 F2=0.5×0.208×2.84×1.2×10.17^2=36.6 [N]

となります。

3.加速抵抗

速度を変化させる際に発生している抗力。

F3=加速度(a)×(車重(w)+等価慣性質量(wi)) ・・・④

と定義されています。

加速度は2.と同じくWLTCモードのデータから考えます。

WLTCのRPA(速度の影響を加味した加速度平均値)は0.167です。今回は③では速度を一定としてますが、加速度は別途発生していると仮定してa=0.167 m/s2とします。

等価慣性質量はモータやタイヤ等の慣性抵抗を質量に換算して組み込むことになります。こちらは厳密には図面や材料密度から読み取るべき値になりますが、標準的には車両質量の8 %程とされています。 以上より

F3=0.167×(2190×1.08+100)=411.7 [N]

となります。

4.勾配抵抗

登坂する際に発生する抗力。こちらは車両を走行させる状況の影響が著しく大きいため省略します。

以上より、抵抗としてかかる力はF1+F2+F3=560.5 Nとなり、これより1 m動かすときに必要な仕事は560.5 Jと計算が出来ました。

次に分子について考えます。テスラモデルSのバッテリ容量は公式カタログで

100 kwh=360 MJ

と記述されています。2024年現在比較的充電が長持ちするスマートフォンのバッテリ容量が4 wh程度であることを考えると相当積載していることが分かります。

このエネルギーを使って走行しますが、ここで注意したい点としては残念ながらエネルギーの100 %を走ることに消費できる訳ではない、ということです。例えば車内空調等走行以外に関わる機器で活用される分や、バッテリやモータにおいて熱や振動、音等損失として消えてしまう分を差し引く必要があります。

今回は代表例として主たるエネルギー消費先と見込まれるモータの損失を調査してみましょう。

モータの損失はトルクや回転数によって変動しますが、今回使用されているモータに関しては95 %程度の効率があるとの報告がありましたのでこの値を参考にすると、

360×0.95=342 MJ

が実際に走行に使用されるエネルギーとなります。

以上より、一度の満充電で走行できる距離は

360×1e6×0.95/560.5/1000=610.2 kmと導出が出来ました。

答え合わせとして、ここで改めてカタログに載っている航続距離を確認してみますと634 kmとなっており、ある程度近い値となっています。このように公開情報を用いることで、ある程度近しい値を推測できることが分かりました。

更なる解像度を求める場合

さて、ここから更に解の解像度を上げようとする場合、今回は問題を簡単にしてしまっているところをより詳細に突き詰めていく必要が出てきます。速度/加速度変動をF2,F3を積分形式にすることで折り込む程度であればエクセル等でも可能でしょうが、

• 今回は無視した各構成要素のエネルギー損失を取り込む
• 電池の外部環境依存性やよりリアルな挙動(リチウムイオン電池の特性上蓄えられたエネルギーを100%使い切ることはできない 等)を再現するように厳密なモデルを計算式に導入する
• アクセル/ブレーキの制御の仕方による影響を盛り込む

等等より確度を挙げるための対策は多岐に渡ります。これら全てを考慮するには、より専門性の高いソフト・手法を使用する必要が出てくるでしょう。実際の自動車設計では開発初期の段階においてモデルベース開発(MBD)的な手法を用いることで検証することが良く行われています。

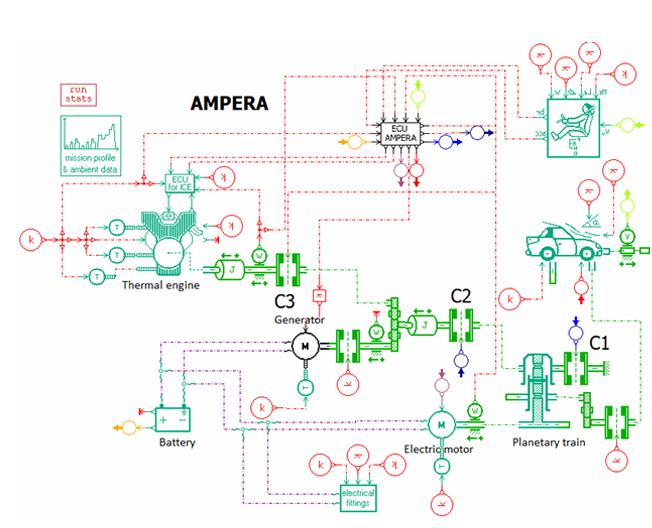
モデルベースによる電燃費シミュレーションの例：F. Badin, et al.,World Electric Vehicle Journal 7(3):475-488 より抜粋

まとめ

このように公開されている情報を突き合わせて、理論的に組み立てることだけでも様々なことが分かります。ぜひ技術者の方々は、安易にシミュレーションを実行するだけではなく、公知情報から値の予測をして、解析することに価値があるかどうかの判断を下せるようになりましょう。

追記；この記事を書いてから知りましたが、若干不穏当な表現をすると、諜報分野ではこのように合法的な公開情報を集めることで対象を分析することをオープン・ソース・インテリジェンス(OSINT)と呼ぶそうです。このように公開情報から隠匿情報を推測されないように、企業として情報の公開する範囲は改めて慎重に選ぶ必要があるな、と再考させられる機会になりました。