はじめに
「有限要素法 (Finite Element Method, FEM)」と聞くと、機械設計に関心のある方であれば、構造解析を思い浮かべる方が多いと思います。中には、「有限要素法=構造解析の計算手法」と考えている方もいるかもしれません。しかしながら、有限要素法とはあくまで偏微分方程式を離散的に解く方法の一つですので、数値流体力学(Computational Fluid Dynamics, CFD)や電磁界解析など、構造解析以外の計算にも適用可能です。
同じく偏微分方程式を離散的に解く方法には、有限要素法の他にも、有限差分法 (Finite Difference Method, FDM)や有限体積法(Finite Volume Method, FVM)などといった手法があります。特に、有限体積法は商用・非商用問わず今日の実用的な流体解析ソルバーにおいては最も広く用いられる手法です。では、なぜ構造解析では有限要素法が主に用いられるのに対して、CFDでは有限体積法が広く用いられているのでしょうか。
実は、CFDにおいてどちらの方法が優れているのかは結論がついているものではなく、有限要素法のCFDへの適用については今でも世界中で日夜研究が行われています。そのため現在では、多くの場合、有限体積法を採用する理由は「既存の資産(先人の文献やプログラムなど)を利用したいから」「コミュニティが大きいから」等の人的な理由になるのかもしれませんが、CFD黎明期から有限体積法を選ぶ方向の潮流が生まれたのには何か別の理由があったはずです。
本記事では、CFDにおける有限要素法と有限体積法の基本的な定式を比較して「なぜCFDでは有限体積法が一般的になったのか」の理由を垣間見ていきます。
式の比較
以下の式で表される、1次元の偏微分方程式を考えます。
\tag{1}\frac{\partial\phi}{\partial t}+\frac{\partial f}{\partial x}=0ここで\phi=\phi(t,x)は物理量、tは時間、xは座標、f=f(\phi)は流束を表しています。
有限要素法の定式
この式を有限要素法で解くには、任意の重み関数w(x)を掛けた上で計算領域\Omega全体で積分を行います。
\tag{2}\int_\Omega w(x)\left(\frac{\partial\phi^n}{\partial t}+\frac{\partial f^n}{\partial x}\right)dx=0上付き文字のnはステップ数を表しています。有限要素法では、基底関数N(x)を用いて要素内の物理量の分布を補間します。
\tag{3}w(x)=N_i(x)w_i \\
\phi^n(x)=N_j(x)\phi_j^nここでi,jは要素番号で、アインシュタインの総和規約を適用しています。これらの式を起点として支配方程式の定式化を行います[1]。基底関数により要素内の物理量の分布を補間する部分が有限要素法の大きな特徴の一つです。その基底関数N(x)は多項式を用いるのが一般的ですが、その多項式の次数を増やすことで、高次の補間の定式化を行うことが有限体積法よりも容易にできます。
有限体積法の定式
一方、有限体積法では、重み関数を掛けずに式(1)を各計算セル(要素)\!^1 内で積分します\,^2。
\tag{4}\int_{\Omega_i} \frac{\partial\bar\phi_i^n}{\partial t}dx_i+\int_{\Omega_i}\frac{\partial f_i^n}{\partial x}dx_i=0有限体積法では基本的には解をある点における値ではなくセル内の平均値として定義するため、平均値を表すバー(‾)を\phiにつけています。左辺第二項をガウスの発散定理により境界積分に書き直すことで、有限体積法で解くべき式は以下のようになります。
\tag{5}\int_{\Omega_i} \frac{\partial\bar\phi^n_i}{\partial t}dx_i+\int_{\Gamma_i} \tilde f_i^n ds_i=0\tilde fはセル界面を通る流束である数値流束を表しています(セル代表点での流束である物理流束fとは区別してチルダを付けています)。また、\Gamma_iはセルiの境界、ds_iはセルiの境界の単位法線ベクトルを表しています。この式は解\bar\phi^nの変化はセル界面を通る流れの出入り(流束)のみによって決まることを表しています(下図)。
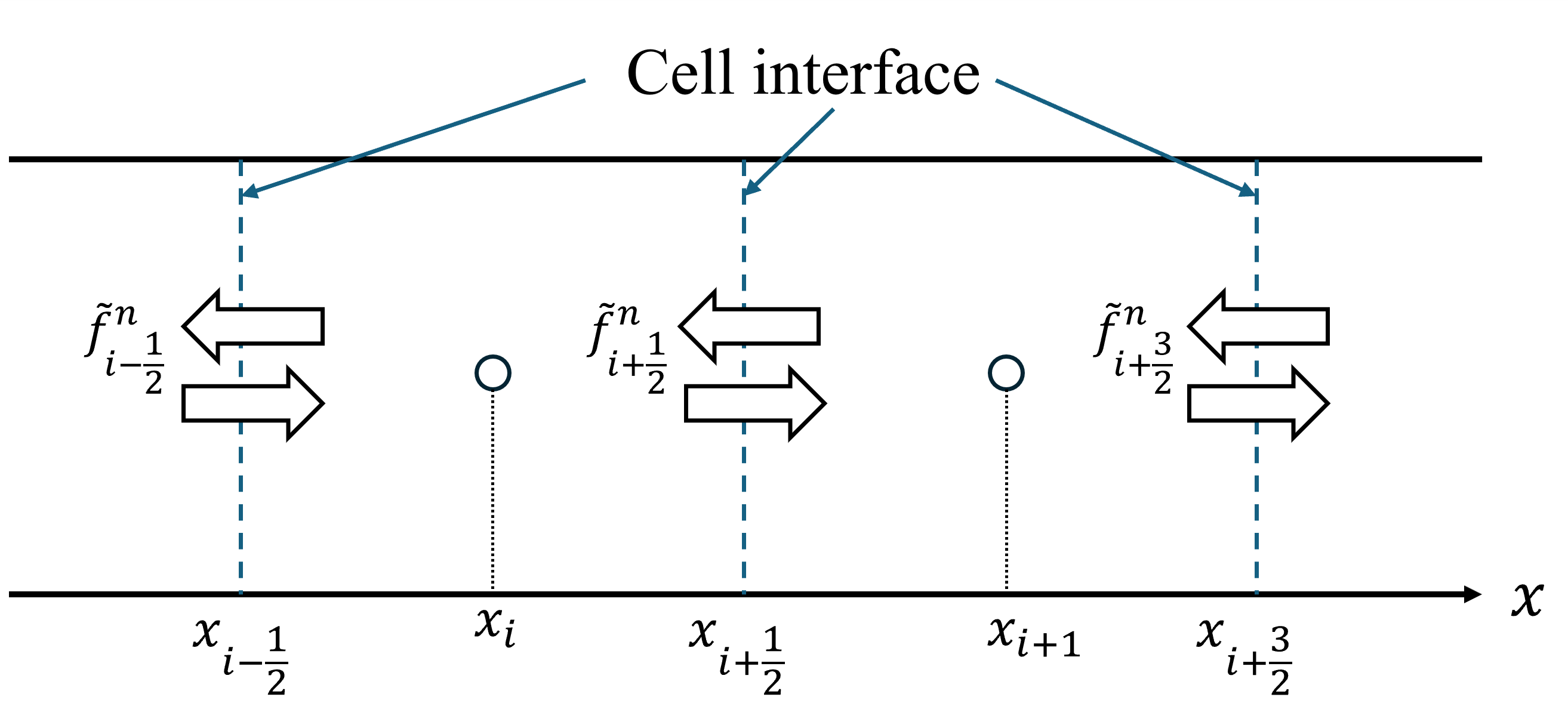
あるセルから出る流れは隣接するセルに入る流れと大きさは等しく符号は逆になるため、式(5)の全てのセルの総和をとれば、各セル界面の流れの出入りがキャンセルしあうことで、結局式(5)は計算領域全体でも成り立つことになります。
\tag{6}\int_\Omega \frac{\partial\bar\phi^n}{\partial t}dx+\int_\Gamma \tilde f^n ds=0有限要素法の式(2)は、計算領域全体で保存則が満たされると解釈できる一方で、有限体積法の場合は、式(5),(6)より計算領域全体だけでなく計算セル1つ1つにおいても保存則が成立します\,^3。すなわち、基本的には有限体積法は有限要素法よりもより厳しく保存則が守られることを意味しています\,^4。流体解析では支配方程式が(質量・運動量・エネルギーの)保存則そのものであることから、直感的には有限体積法を用いる方が自然な選択のように思えます(この感覚も有限体積法が好まれてきた理由の1つかもしれません)。個人的には、有限要素法よりも有限体積法の定式の方が物理的な解釈が容易なので、それも有限体積法の参入障壁を下げてコミュニティの拡大に寄与したのではないかと想像しています。
有限要素法と比べた時の有限体積法の大きな特徴の一つとして、有限体積法では各セル界面における流束(数値流束)を陽的に計算するという点が挙げられます。その計算方法には任意性があるのが有限体積法の難しい(そして面白い)ところであり、同時に利点になるところでもあります。
\,^1 節点に囲まれた領域を有限要素法では「要素」、有限体積法では「セル」と呼ぶことが一般的です。
\,^2 注目する要素内ではw_i(x)=1, その外ではw_i(x)=0となる重み関数を掛けて計算領域全体で積分するという解釈もできます。すると、有限体積法は有限要素法のある特殊な場合であると言えます。
\,^3 離散化の方法によってはこの局所的・大域的な保存性は満たされなくなります。例えば非保存形式の支配方程式を離散化した場合[2]。
\,^4 局所の保存性が満たされないと、局所的に非物理的なソース項が生じて計算が不安定になる場合があります。
計算してみる
それでは、有限要素法と有限体積法の定式の違いがわかったところで、実際にそれらを用いて単純な流れを解いてみましょう。有限要素法と有限体積法の有意な比較をすることは容易ではないので、ここではそれぞれの性能の比較ではなく、両者別々にとりあげてそれぞれの手法にどのような利点があるのかに着目します。
有限要素法での計算
まずは有限要素法を扱います。支配方程式は以下に示す一次元移流拡散方程式とします。
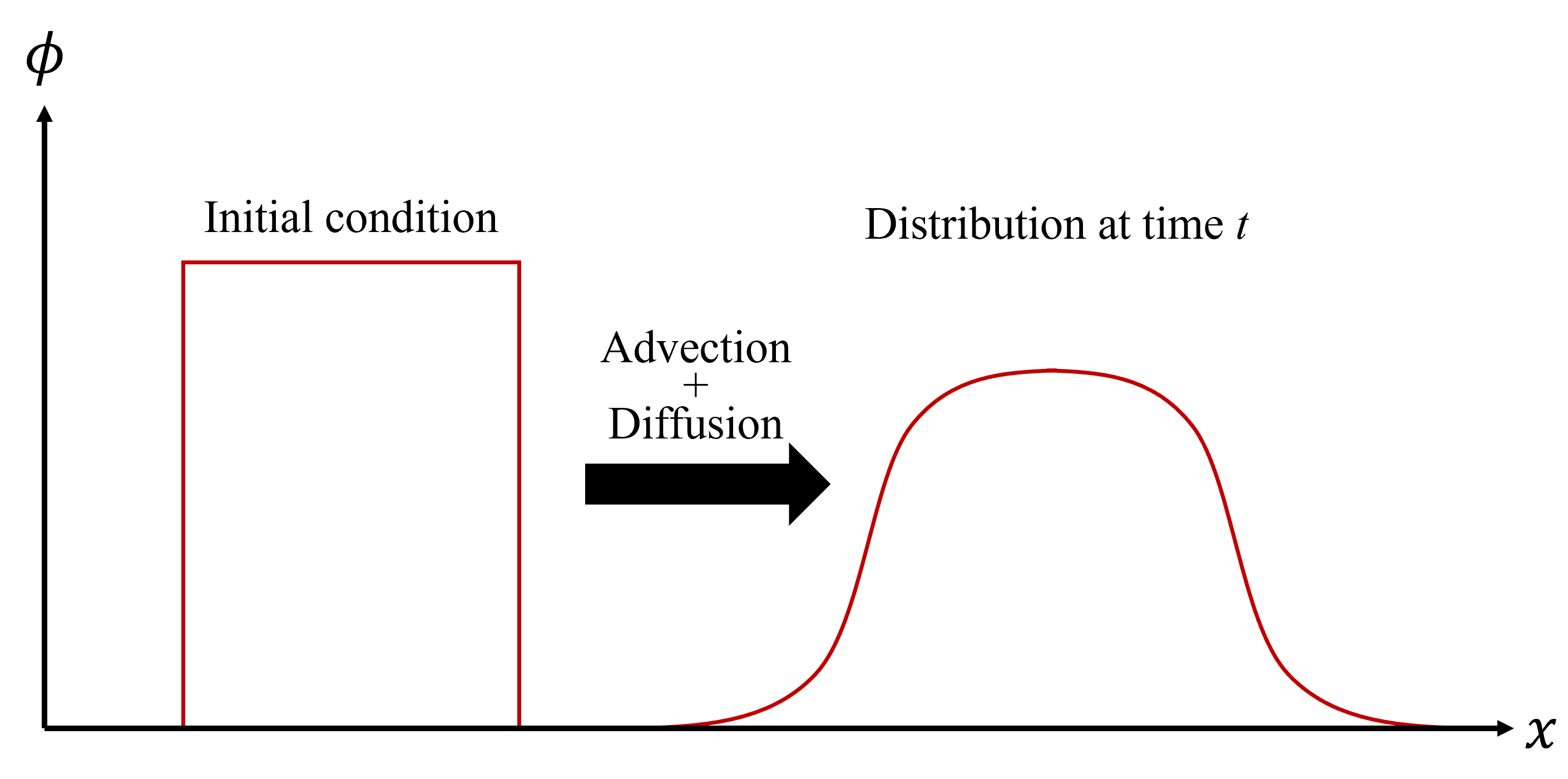
\tag{7}\frac{\partial\phi}{\partial t}+c\frac{\partial\phi}{\partial x}=\alpha\frac{\partial^2\phi}{\partial x^2} この式は下図のように物理量\phiの初期分布が速度cで移動しながら拡散係数\alphaで拡散していくことを表しています(c, \alphaは定数)。
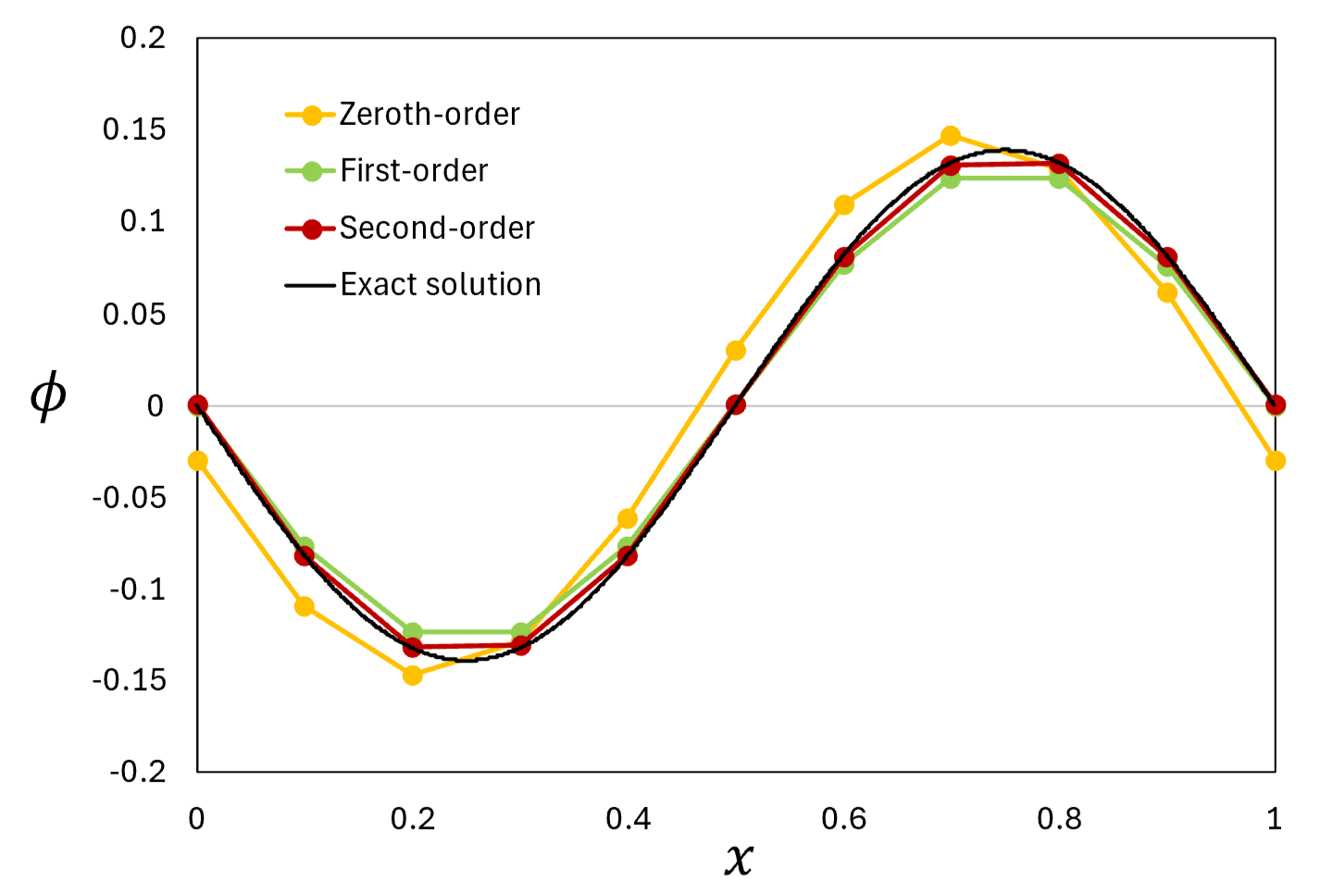
下図は物理量\phiの初期分布を\phi(x)=\mathrm{sin}(2\pi x)\quad(0\le x\le1)として、周期境界条件の下で節点数11, c=1.0, \alpha=0.1, また時間刻み\Delta t=5.0\times10^{-5}で t=0.5における解を0次(要素内一定)\,^1、1次(線形近似)、2次(二次曲線近似)補間を用いて求めた時の\phi分布です。
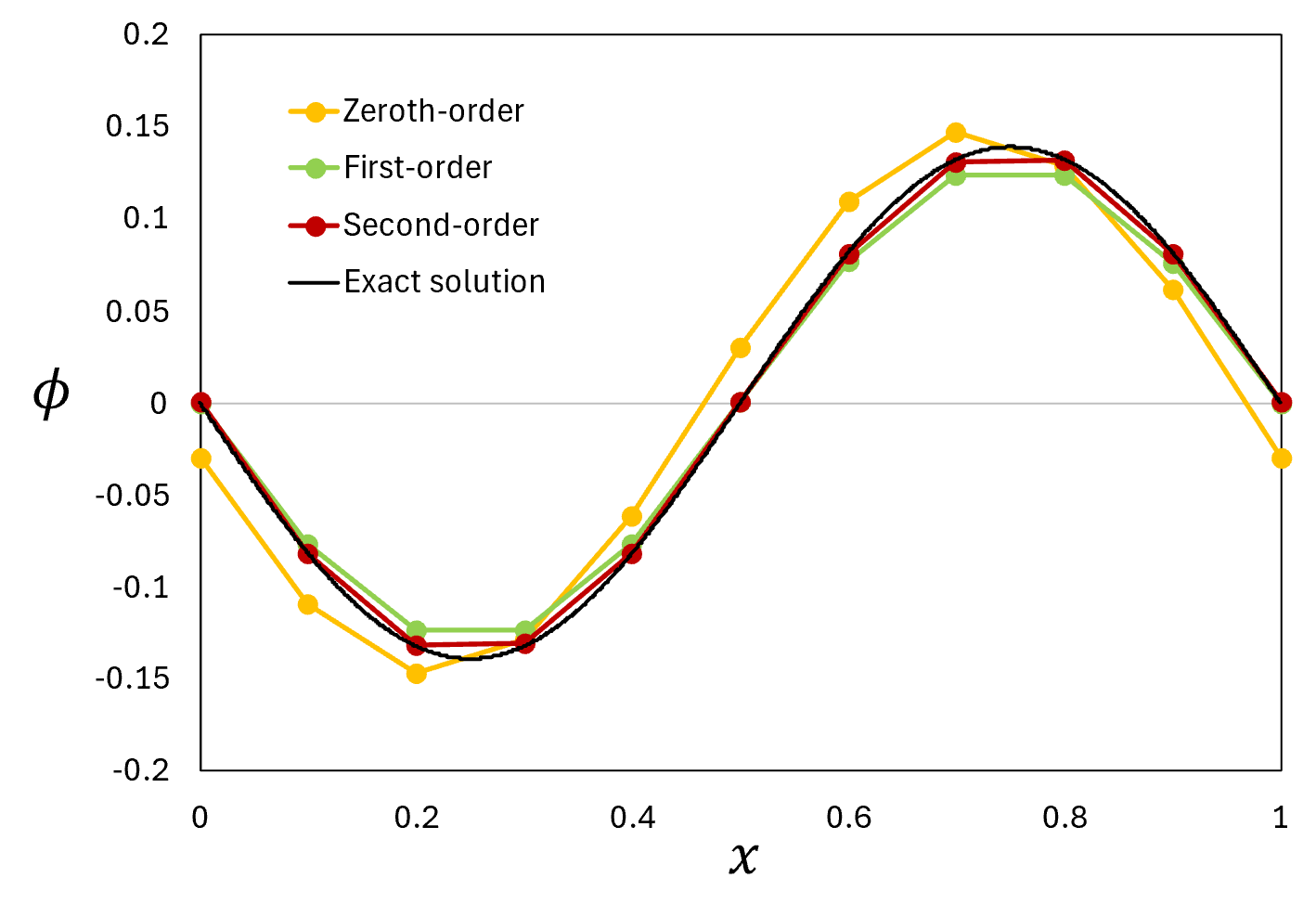
\phi(x)=\mathrm{sin}(2\pi x)\quad(0\le x\le1)を初期分布とした移流拡散方程式の計算結果(t=0.5)
補間の次数が上がるとより解析解に近づく結果になりました。前述のように、有限要素法では要素内の物理量の分布を補間して計算を行います。その時に区分的多項式を用いて補間すると、多項式の次数を大きくすることで、2次補間よりもっと高次の定式化を行うことができます。有限体積法では精度の高い定式を作ることは有限要素法ほど容易ではないため、それが有限要素法の強みの1つと言えます。
有限体積法での計算
次に有限体積法を用いて流れを解きます。支配方程式は以下に示す一次元非粘性バーガース方程式とします。
\tag{8}\frac{\partial\phi}{\partial t}+\frac{\partial}{\partial x}\left(\frac{\phi^2}{2}\right)=0 この式は物理量\phiの初期分布を\mathrm{sin}(2\pi x)\quad(0\le x\le1)とすると下図のように時間発展し、ある時刻以降にx=0.5に物理量\phiの不連続なジャンプ(衝撃波)を形成します。
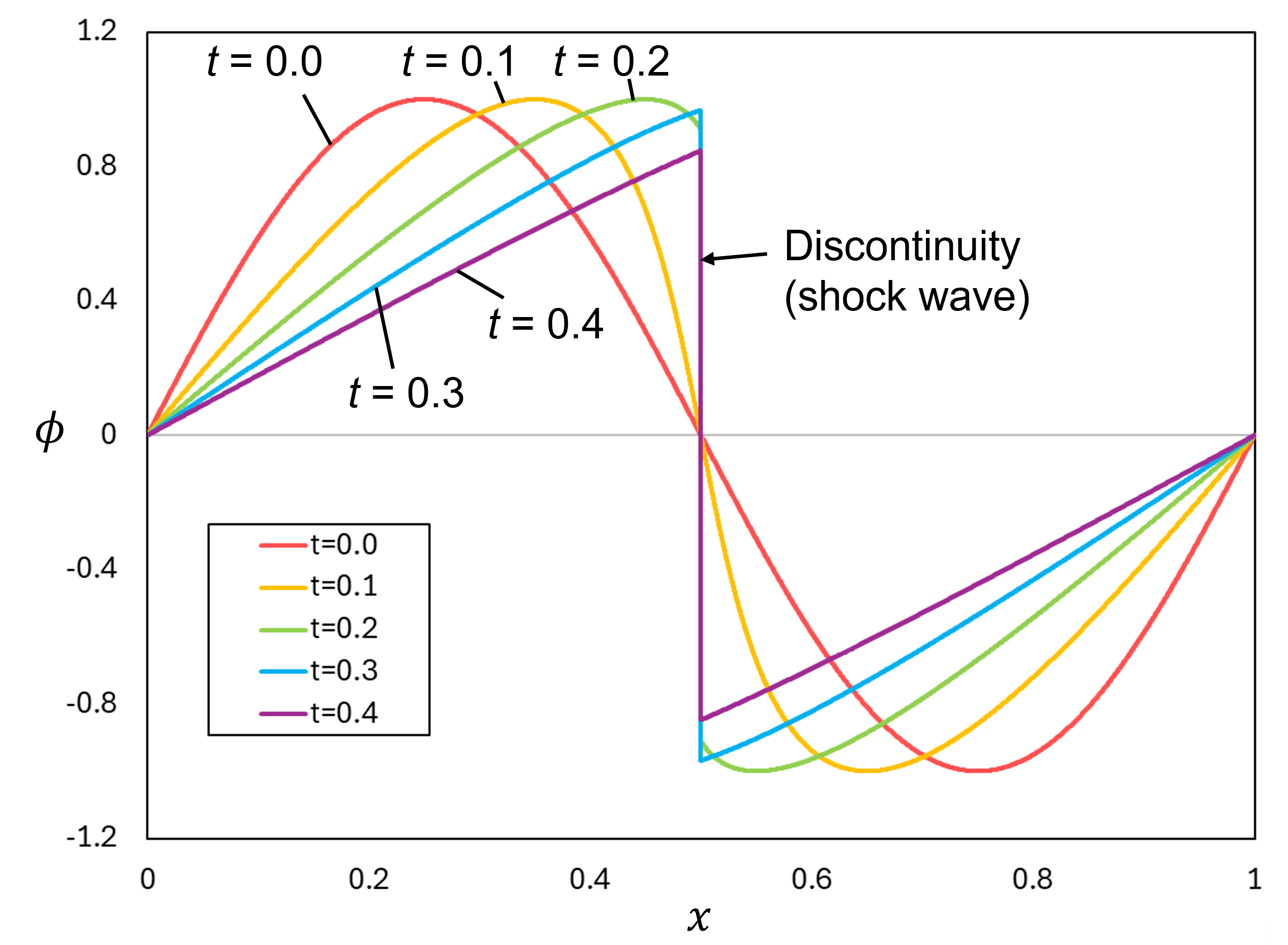
\phi(x)=\mathrm{sin}(2\pi x)を初期分布とした非粘性バーガース方程式の時間発展
前述のように、有限体積法では、セル界面の流束(数値流束)を計算しなければならず、その方法には任意性があります。例えばセル番号iとi+1の間の数値流束\tilde f_{i+\frac{1}{2}}を求める時、\tilde f_{i+\frac{1}{2}}=\tilde f(\frac{\bar\phi_i+\bar\phi_{i+1}}{2})としても\tilde f_{i+\frac{1}{2}}=\frac{f(\bar\phi_i)+f(\bar\phi_{i+1})}{2}としても解は得られます\,^2。また、これらのような算術平均に基づく定式ではなく、流れが来る上流側の物理量を用いて計算する風上法も以下のように容易に定式化できます。
\tag{9}\tilde f_{i+\frac{1}{2}}=\frac{1}{2}\left(\frac{\bar\phi_{i+1}^2}{2}+\frac{\bar\phi_i^2}{2}\right)-\left|\frac{(\bar\phi_{i+1}+\bar\phi_i)}{2}\right| \frac{(\bar\phi_{i+1}-\bar\phi_i)}{2}この式は、\phi_{i+\frac{1}{2}}=\frac{(\bar\phi_{i+1}+\bar\phi_i)}{2}\gt0の時\tilde f_{i+\frac{1}{2}}=\frac{\bar\phi_i^2}{2}=f_iに、\phi_{i+\frac{1}{2}}\lt0の時\tilde f_{i+\frac{1}{2}}=f_{i+1}になります。これらの式を用いて、\phi(x)=\mathrm{sin}(2\pi x)\quad(0\le x\le1)を初期分布として節点数101かつ時間刻み\Delta t=1.0\times10^{-3}でt=0.2における流れを解いたものが下図になります。
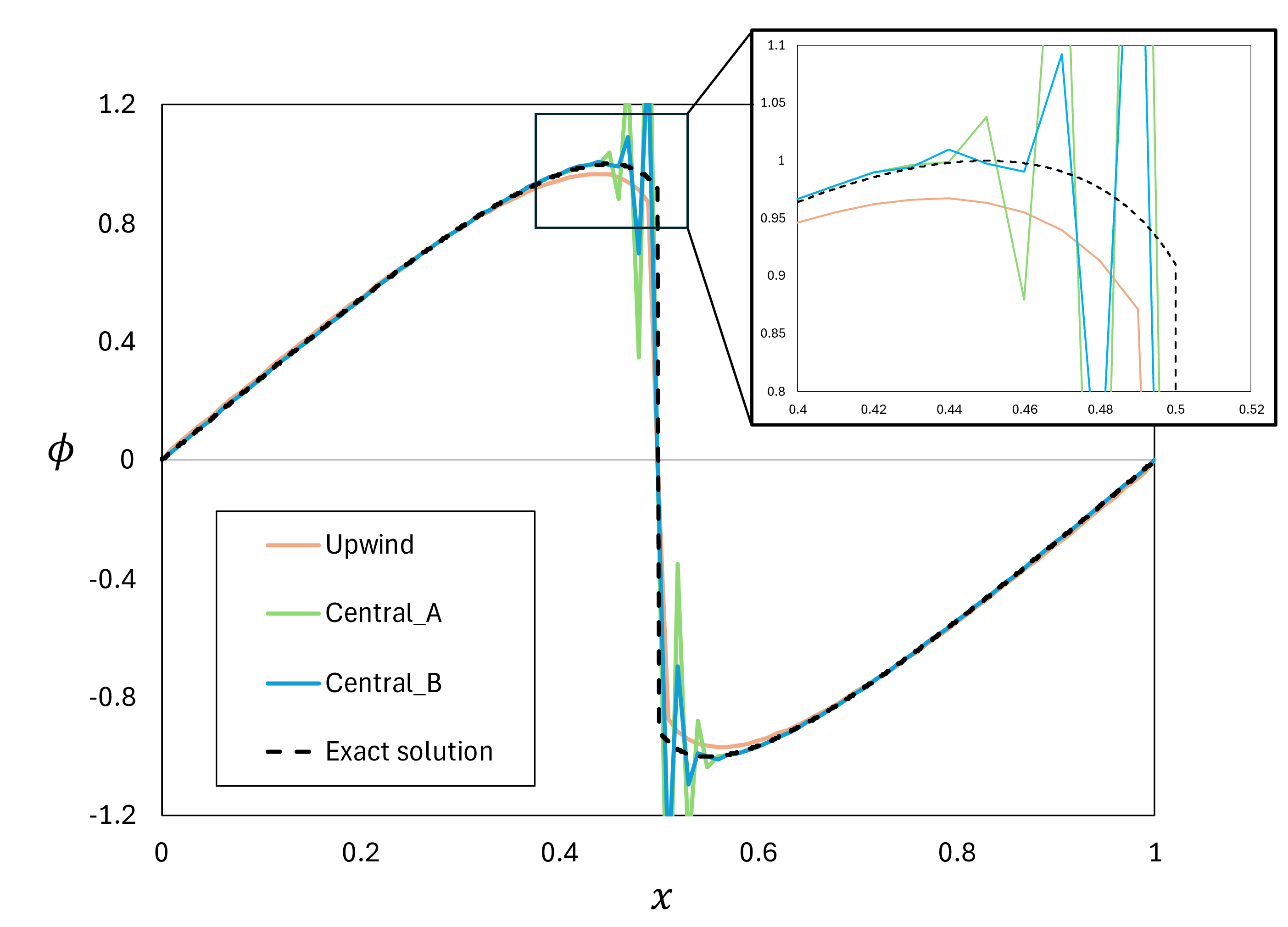
\tilde f_{i+\frac{1}{2}}=\tilde f((\bar\phi_i+\bar\phi_{i+1})/2), Central_Bは\tilde f_{i+\frac{1}{2}}=(f(\bar\phi_i)+f(\bar\phi_{i+1}))/2を表している。
算術平均に基づく定式(Central_AとCentral_B)では物理量が急に変化する部分で振動が生じてしまいました。風上法では振動は無くなりましたが、解がなまってしまいました。詳細は省きますが、これは風上法では解をなまして計算を安定させる数値粘性が生じることに起因します。であれば、物理量が急激に変化する部分でのみ風上法になる計算手法があれば、計算精度を保った上で安定な計算ができるように思えますね。有限体積法では、そのようなアイデアを以下のように簡単に実現することができます(ただし、今回の問題設定では以下の説明で得られる定式は有限差分法と同一になります)。
風上法の式(9)をよく見ると、右辺第一項は物理流束f_{i+1}とf_iの算術平均(図5のCentral_Bと同一)であることから、第二項は実質的に数値粘性を含む項だと考えられます。そこで、局所の物理量の勾配に応じて数値粘性の大きさを変えられるように、以下のように第二項に制限関数L(r_{i+\frac{1}{2}})をかけてみます。
\tag{10}\tilde f_{i+\frac{1}{2}}=\frac{1}{2}\left(\frac{\bar\phi_{i+1}^2}{2}+\frac{\bar\phi_i^2}{2}\right)-L(r_{i+\frac{1}{2}})\left|\frac{(\bar\phi_{i+1}+\bar\phi_i)}{2}\right| \frac{(\bar\phi_{i+1}-\bar\phi_i)}{2}ここでL(r_{i+\frac{1}{2}})はr_{i+\frac{1}{2}}=\frac{\phi_i-\phi_{i-1}}{\phi_{i+1}-\phi_i}の関数です。物理量が急激に変化する場所ではL(r_{i+\frac{1}{2}})=1で風上法となり、物理量が滑らかに変化する場所ではL(r_{i+\frac{1}{2}})=0で算術平均になるような関数を設定してみます。関数の中身には任意性がありますが、ここでは
\tag{11}L(r)=1-\mathrm{max}[0,\mathrm{min}(1,r)] とします\,^3。この式を用いて同じ流れを解くと以下の図のようになります。
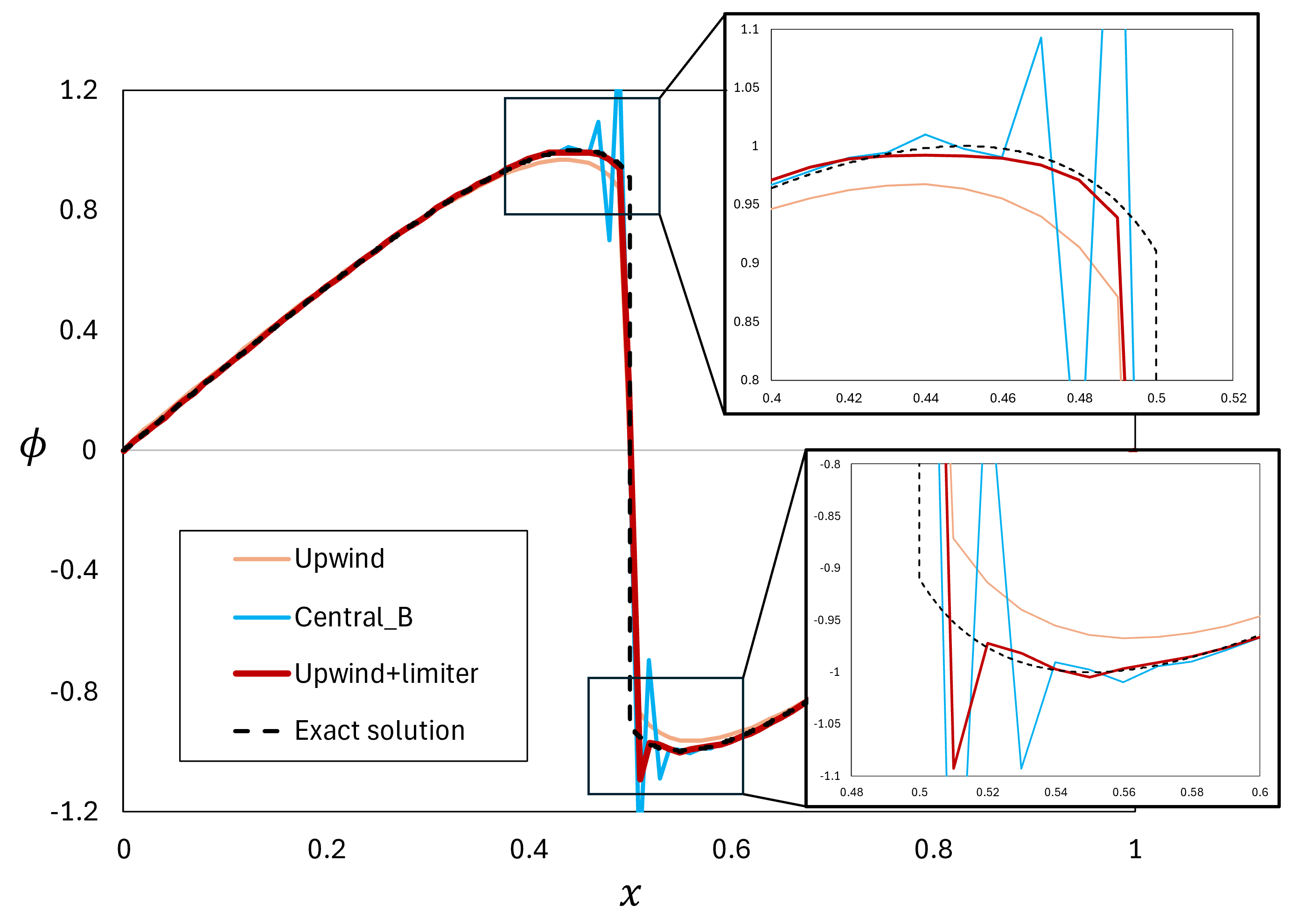
まだx=0.52付近で振動は残っているものの、算術平均(Central_B)よりも振動が小さく、また風上法よりも高精度で流れを解くことができました。
以上の例のように、基本的な有限体積法のアルゴリズムでは、数値流束を陽に計算するため、局所の流れ場の情報を反映させた計算手法を組み込むことが容易にできます。流体の運動を表すNavier–Stokes方程式は非線形性が非常に強いので、計算領域内に局所的に生じた複雑な物理現象に対して安定に計算し続けられるような対処が実装上容易だったことが、有限体積法が有限要素法よりも好まれた理由の1つなのだと考えられます。そのようにして有限体積法のコミュニティが拡大したことが、CFDで有限体積法が一般的になる一助になったのではないでしょうか。
\,^1 1次補間で集中化質量行列を用いることに相当します。また今回の問題設定では、0次補間で得られる定式は、時間は一次精度前進差分法かつ空間は二次精度中心差分法で離散化した有限差分法・有限体積法と同じ定式になります。
\,^2 後者は有限差分法で二次精度中心差分法を用いた定式と同一になります。
\,^3 右辺第二項はminmod関数と言います。
おわりに
本記事では、有限要素法と有限体積法の基本的な定式・強みの違いを比較して、CFDで有限体積法が一般的になった理由の一端を探ってみました。
今回触れたのはあくまで有限体積法と有限要素法の違いの一部であり、またそれぞれのアルゴリズムの基本的(古典的)な部分のみを見てきました。現在では有限要素法・有限体積法共に発展し続けており、両手法がお互いの強みも持ち合わせた手法が提案されていたりと、CFDの計算手法の研究は止まるところを知りません。
前述のように、流体解析において有限要素法と有限体積法のどちらが優れているかは結論がついているものではなく、今後有限要素法が優勢になる可能性もありますし、やはり有限体積法が一般的であり続ける可能性もあります。もしかしたら両者でもなく別の計算手法が一般的になるかもしれません。いずれにしても、CFDを行う上では計算手法の中身を理解した上で、計算する対象の物理に合わせて適切な手法を選択することが重要です。
参考文献
[1] 河野晴彦,“詳解 流れの数値計算 - 有限要素法による非圧縮性流体解析の基礎 -”,コロナ社,2022,pp. 46–100.
[2] Hirsch, C., Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics, 2nd ed., Butterworth-Heinemann, 2007, pp. 206–208.