JP EN
最適化の設定について考えよう

最適化の設定について考えよう

Let's think about optimization settings.

皆さんは Grasshopper で最適化をしたことがありますか？特に Tunny をつかって最適化をしたことがありますか？ その時にうまく最適化できないなと思ったことはないでしょうか。 Tunny が採用しているブラックボックス最適化と呼ばれる部類の最適化は感度を使用した最適化（例えば位相最適化）に対して収束が遅いため、適切な最適化設定でなかったり、対象の問題が適切でないと、ランダムより少し良い結果が得られる程度のものになってしまいます。 今回は Tunny を使って、最適化設定の違いによる結果の違いを見ていきましょう。

Have you ever performed optimization in Grasshopper? Specifically, have you used Tunny for optimization? During that time, did you ever feel that the optimization was not working well? The category of optimization called black-box optimization, which Tunny uses, has slower convergence compared to sensitivity-based optimization (such as topology optimization). If the settings are not properly configured or the problem is not suitable, the result may end up being just slightly better than random. In this article, let's look at the optimization results using Tunny with different settings.

夏目大彰

Hiroaki Natsume

2024,04,05 2024,04,05

どんな最適化に向いているか

設定について考える前に、そもそも Tunny で使用可能な最適化手法そのものの得意不得意を確認します。

Tunny はたくさんの最適化手法に対応しているので、どれを選べばよいか悩むことがあります。 公式ページにあるそれぞれの得意不得意と、私が作成した選択のフローチャートをまず記載します。

公式のサンプラーごとの特徴（抜粋）

RandomSampler TPESampler CmaEsSampler NSGAIISampler GPSampler BoTorchSampler
Float parameters ✓ ✓ ✓ ▴ ✓ ✓
Integer parameters ✓ ✓ ✓ ▴ ✓ ▴
Categorical parameters ✓ ✓ ▴ ✓ ✓ ▴
Pruning ✓ ✓ ▴ × ▴ ▴
Multivariate optimization ▴ ✓ ✓ ▴ ✓ ✓
Conditional search space ✓ ✓ ▴ ▴ ▴ ▴
Multi-objective optimization ✓ ✓ × ✓ (▴ for single-objective) × ✓
Batch optimization ✓ ✓ ✓ ✓ ▴ ✓
Distributed optimization ✓ ✓ ✓ ✓ ▴ ✓
Constrained optimization × ✓ × ✓ × ✓
Recommended budgets (#trials) as many as one likes 100 – 1000 1000 – 10000 100 – 10000 – 500 10 – 100

選択のフローチャート

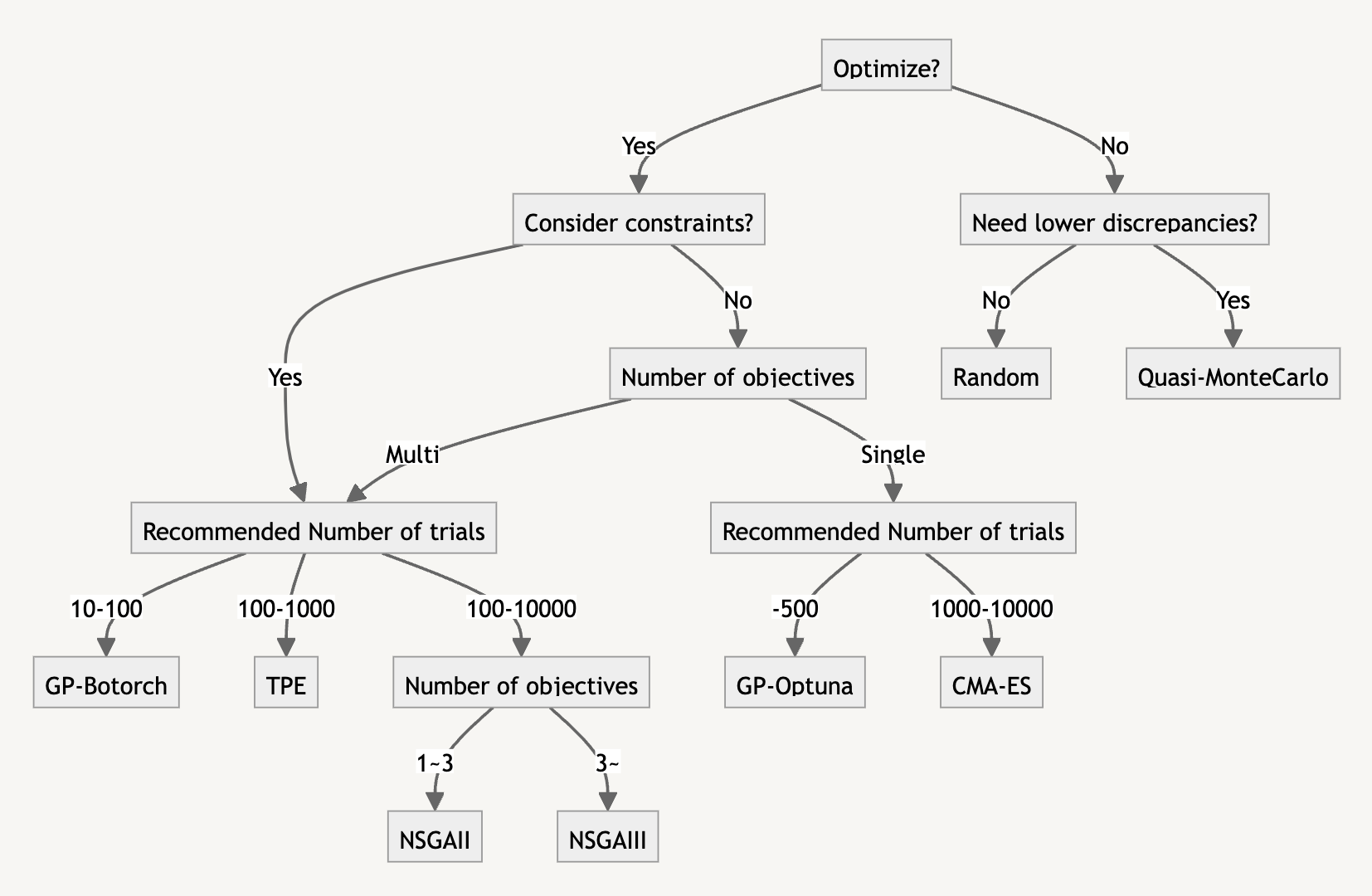
フローチャートはまずこれを試してみた方が良い程度の指標です。 実際に扱おうしている問題に必ずしもあっているとは限らないので、いろいろ試してみてください。

では実際に使ってみたときの挙動を見てみましょう。

Tunny のデフォルトでの最適化

Tunny は他の最適化プラグインと異なり、デフォルトの最適化の手法は GA ではなく TPE になっています。 またいろいろな手法がサポートされています。 あまり馴染みがない方も多いと思いますので、ここでは設定を何もいじらずデフォルトで動作させたときにどうなるか見てみましょう。

最適化の手法を確認する際には色々なベンチマーク関数を使用しますが、そんなことは考えずにただの2つの NumberSlider の和の最小化問題を解いてみましょう。

0~1 の範囲で値を取る NumberSlider ですが、小数点以下 1/10,000 まであります。

file

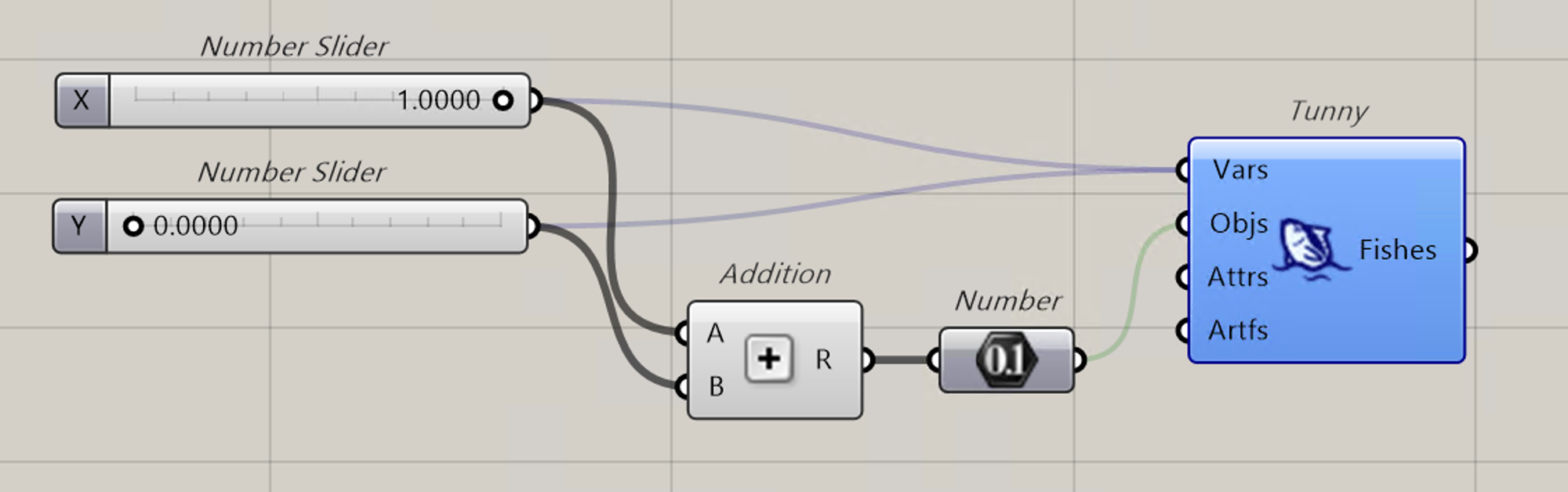
本記事ではA+Bを対象にしていますが、ベンチマーク関数次第で最適化の優劣が変わることが知られています。 そのため、本記事での検討は設定が最適化に与える影響の一例として考えてください。

TPE を使った最適化

では何も考えずに Tunny のデフォルトの設定で最適化を実行してみます。 デフォルトでは以下になっています。

  • 試行回数：100

TPE の設定

  • seed : 自動計算
    • 疑似乱数を生成するアルゴリズムのシード
  • Number of startup trials : 10
    • TPE で探索する前のランダムサンプリングでの初期化の試行数
  • Number of EI candidates : 24
    • 獲得関数を評価する際に使用するサンプリング数
  • Consider Prior : True
    • 探索と活用のトレードオフにおいて探索の比重を高める関数の有効化
  • Prior weight : 1.0
    • 上記関数の重み
  • Consider Endpoints : False
    • True のとき変数の両端を丁寧に探索する
  • Consider Magic Clip : True
    • 最適化計算で使用する分散の値の下限値の有効化
  • Multivariate : False
    • 多変量 TPE の有効化
  • Group : False
    • Multivariate が True のときに探索空間をいくつかの Group に分割した探索の有効化
  • Constant Liar : False
    • 分散並列最適化の効率を上げる Constant Liar アルゴリズムの有効化

最適化は一部で疑似乱数を使っており、実行するたびに結果が変わるので、5 回最適化を実行しています。 なお疑似乱数を生成するシード値を直接指定することもできるため、最適化の再現を行うこともでき、あとの章でこの機能を使っています。

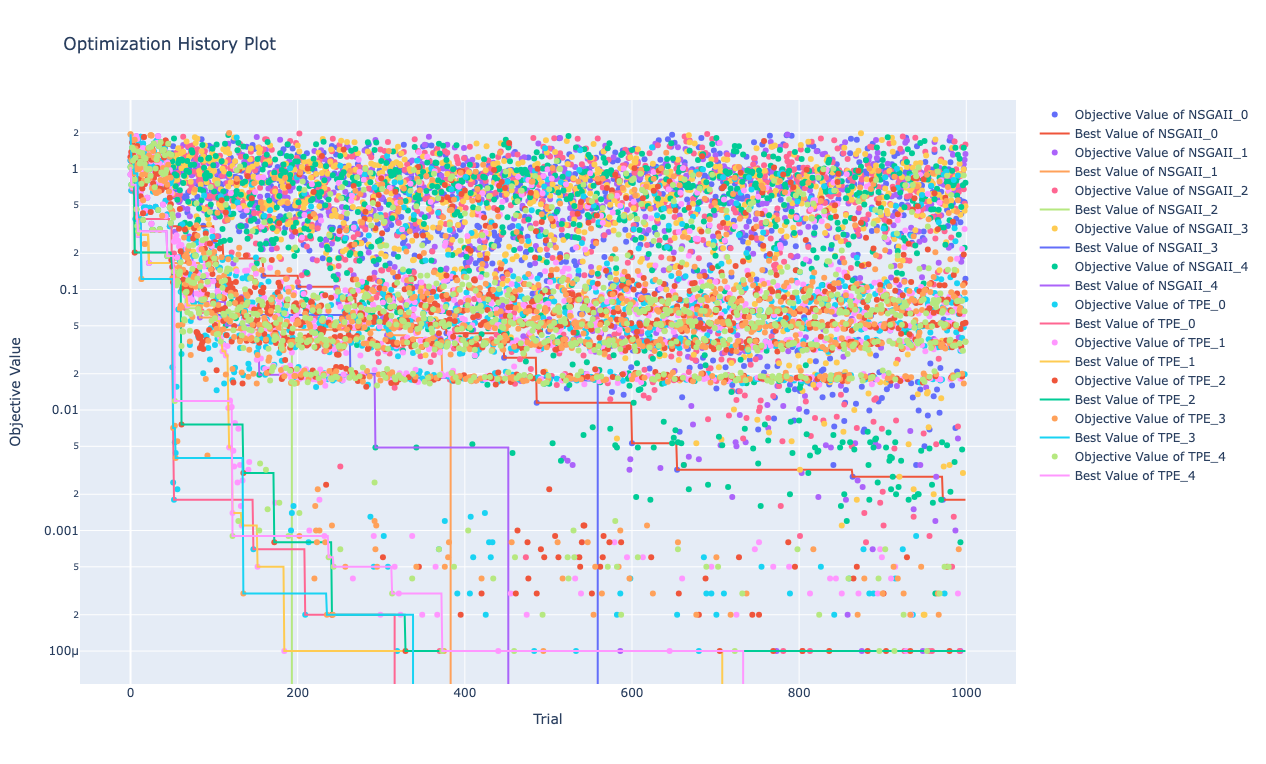
以下のグラフは最適化のヒストリーで、縦軸が目的関数の値（ここでは 2 つの NumberSlider の和）、横軸が試行回数になります。 表示されている線は各最適化で得られている最小値の変化を示したものです。 右に行くほど最適化が進むので、最小値が小さくなっていきます。

なお縦軸は対数軸になっています。

以下の表では、5回最適化を行った結果に加えて、5回中の最小値、平均値、標準偏差をあわせて記載しています。

1 2 3 4 5 minimum Average SD
TPE 0.0108 0.0017 0.0004 0.0211 0.0039 0.0004 0.0076 0.0077

file

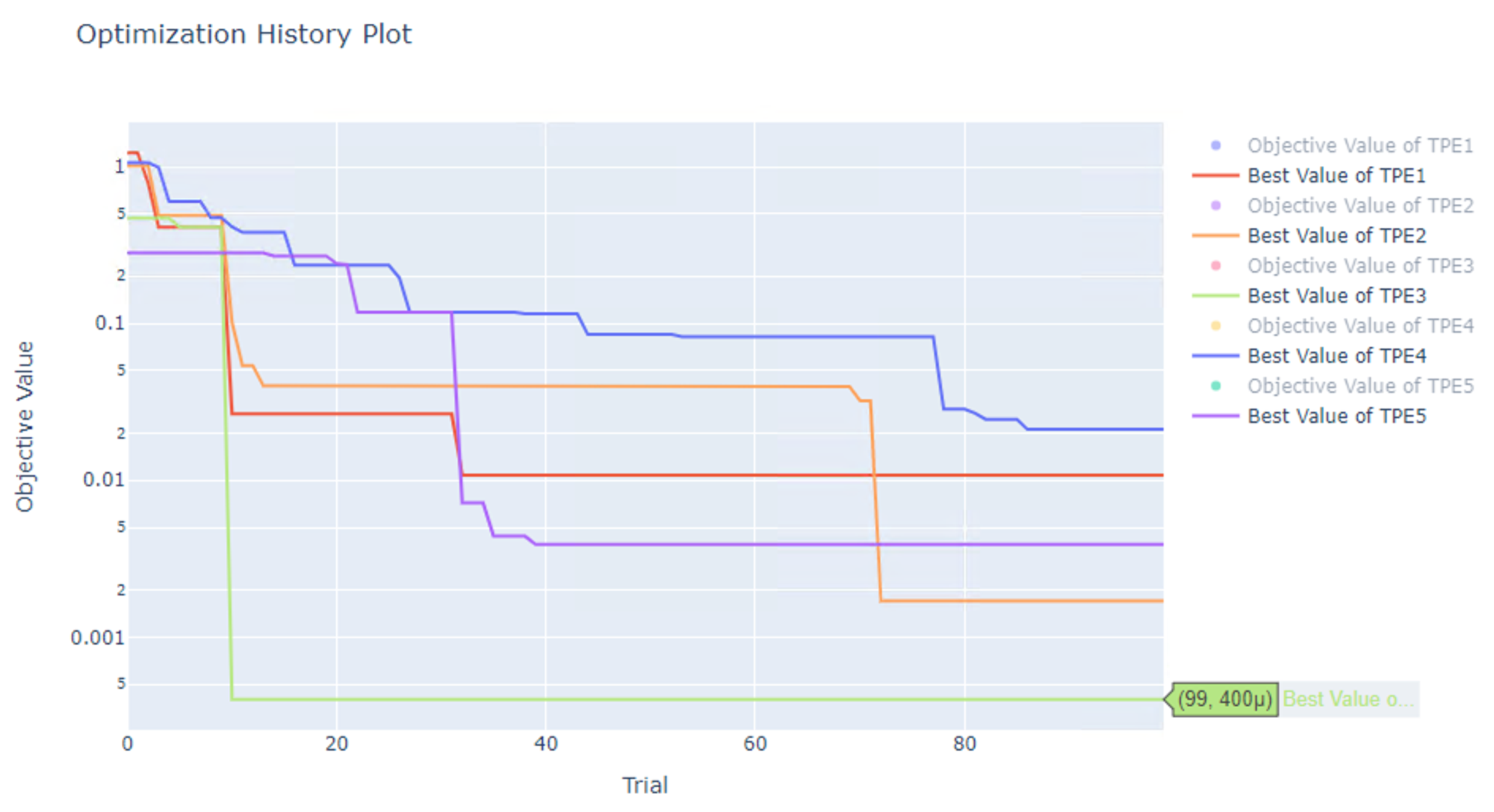
こんな人間なら一目見ただけで最小値になる変数の組み合わせ X=Y=0 がわかる簡単な問題でも、変数の組み合わせが多い（10^4 \times 10^4=10^8通り）とちゃんと0になりません。

GA を使った最適化

同様のことを Grasshopper の最適化でよく使われる GA に該当する NSGAII でも試してみます。

NSGAII のデフォルトでの設定とそれぞれの意味は以下です。

  • seed : 自動計算
    • 疑似乱数を生成するアルゴリズムのシード
  • Mutation Probability : 自動計算
    • 子集団の子個体における突然変異の確率
    • 計算式 p_{mut} = \frac{1}{max(1, d)}
    • d は変数の数
    • 変数が 1 つの場合、突然変異の確率が 1 になりランダムになる
    • 値を直接指定することも可能
  • Crossover Probability : 0.90
    • 子集団の生成における交叉の確率
  • Crossover Method : Uniform Crossover (一様交叉)
    • 子集団の生成における交叉のアルゴリズム
  • Swapping Probability : 0.50
    • 一様交叉において親個体のそれぞれの次元のどちらを採用するかを決定する確率
  • Population Size : 50
    • 各世代での個体数

結果は以下です。GA でも 0 にはなりませんでした。

1 2 3 4 5 minimum Average SD
NSGAII 0.1799 0.1048 0.204 0.0445 0.0857 0.0445 0.1238 0.0595

file

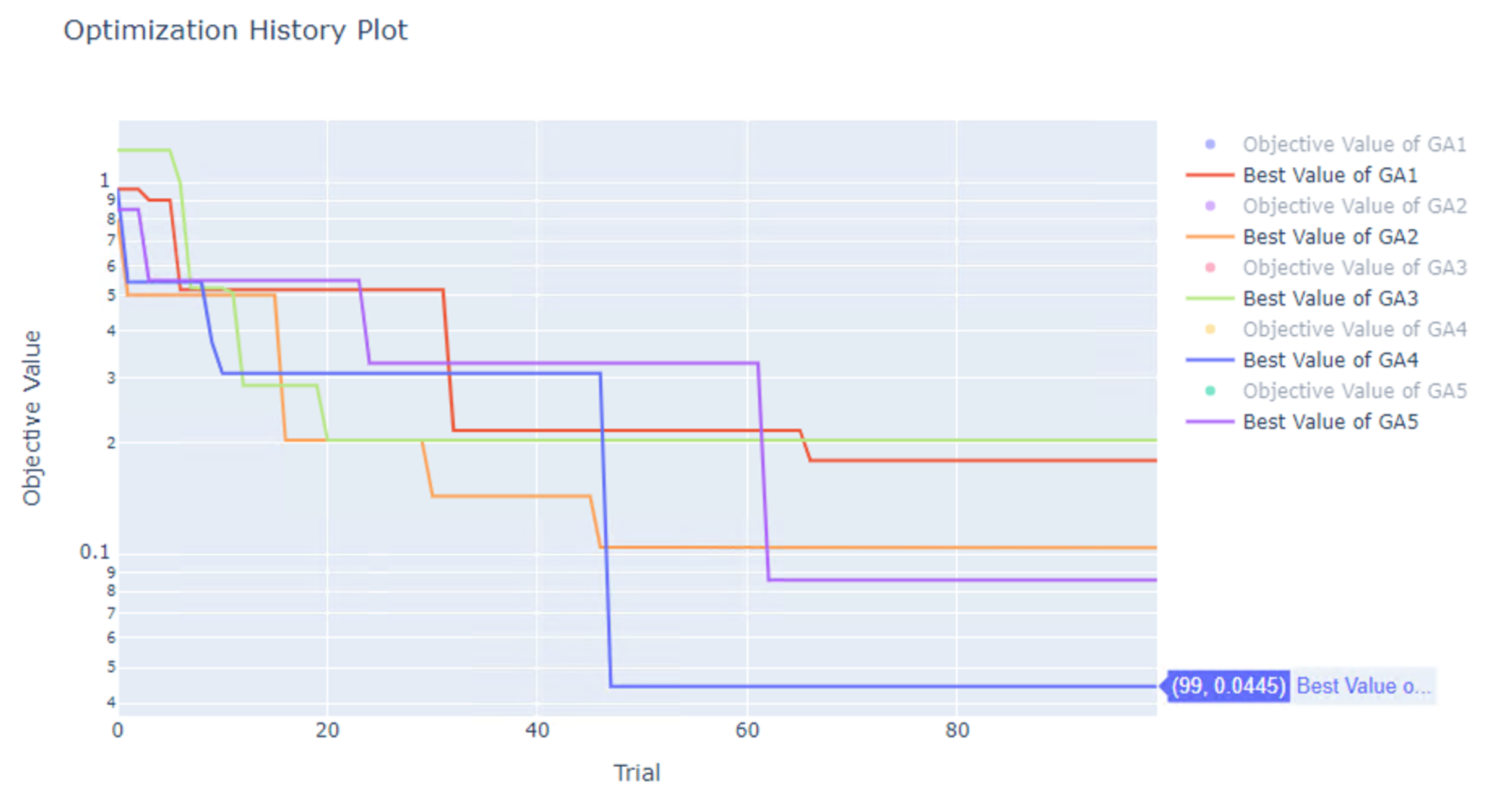
なお、 Tunny の GA のデフォルトは、1 世代 50 個体、合計 2 世代（計 100 個体）になっているため、そのままの設定で GA で最適化するにはあまり適切な設定になっていない中での結果です。

複数の手法での比較

Tunny には他の最適化手法もあるのでそれぞれやってみた結果を以下にまとめました。

1 2 3 4 5 minimum Average SD
TPE 0.0108 0.0017 0.0004 0.0211 0.0039 0.0004 0.0076 0.0077
NSGAII 0.1799 0.1048 0.2040 0.0445 0.0857 0.0445 0.1238 0.0595
Random 0.1315 0.1750 0.1266 0.0974 0.2091 0.0974 0.1479 0.0394
CMA-ES 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
GP-Botorch 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
GP-Optuna 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

GP と CMA-ES は 100 試行でもしっかりと0になる結果が得られましたが、ほかは 0 にはなりませんでした。

TPE は 0 にはなりませんでしたが、5 回行った最適化で TPE、NSGAII、Randomの3つの中で平均値と標準偏差が小さく、4 番目に良い手法でした。

最も平均値が大きい手法はランダムで 0.1479 でしたが、NSGAII の 0.1238 と大きく変わらない結果でした。

最適化時間での比較

以上の結果を見ると 0 になっている 3 つの手法を使用すれば良いと思うかもしれません。 これらの手法の欠点は 100 試行でもかなりの時間がかかることです。 試行を 100 回行うのにかかった時間を以下にまとめています。

sec 1 2 3 4 5 minimum Average SD
TPE 3.00 3.04 3.04 3.11 3.10 3.00 3.06 0.04
NSGAII 2.70 2.77 2.82 2.82 2.71 2.70 2.77 0.05
CMA-ES 41.09 39.87 39.31 40.54 39.99 39.31 40.16 0.61
GP-Botorch 19.80 23.49 20.83 21.65 19.54 19.54 21.06 1.43
GP-Optuna 19.97 19.55 19.80 20.09 24.09 19.55 20.70 1.70
Random 2.32 2.28 2.31 2.34 2.32 2.28 2.32 0.02

100 試行を行う際の時間当たりに期待できる最適値を考えると真の最適解である 0 に到達はしていないですが、TPE は比較的コスパの良い手法になっていることがわかります。

注意事項

  • 上記は100試行でかかる時間ですが、GP の 2 つの手法は 20 試行程度で 0 になるため、0 になる値を取得するまでの時間も実際は早いです。
  • CMA-ES は一般に GP よりも早い手法ですが Tunny のデフォルトで有効になっている withMargin オプションの影響でこの例では GP よりも遅くなっています。
  • 上記結果はあくまで Tunny のデフォルトの設定で最適化を行った場合の結果であって、上記の 6 つの手法のあらゆるケースでの優劣を示したわけではありません。

ではどんな設定なら結果がより良くなるか、次の章では設定をいじって確認してみます。

設定を調整して結果を改善させてみる

たくさん試行する

単純に試行回数が少なかっただけかもしれません。最適化手法の設定は変えず、100試行だったものを、10倍の1000試行でどうなるか試してみます。

対象は 100 試行では 0 にならなかった TPE、NSGAII、Random の 3 つです。 結果を以下の表にまとめています。

他のプラグインでの GA の設定は、世代数と各世代の個体数を指定します。 しかし Tunny では、各世代の個体数と総試行回数しか指定できません。 世代数は、総試行回数/個体数で決定します。

100 試行のときはデフォルトでは 1 世代 50 個体の設定のため、2世代目までしか最適化していませんでした。 今回は1000試行行うので、20世代分の計算を行っています。

結果表

1 2 3 4 5 minimum Average SD
TPE 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
NSGAII 0.0092 0.0180 0.0041 0.0040 0.0034 0.0034 0.0077 0.0055
Random 0.0640 0.0331 0.0465 0.0174 0.0200 0.0174 0.0362 0.0173

TPE ヒストリー

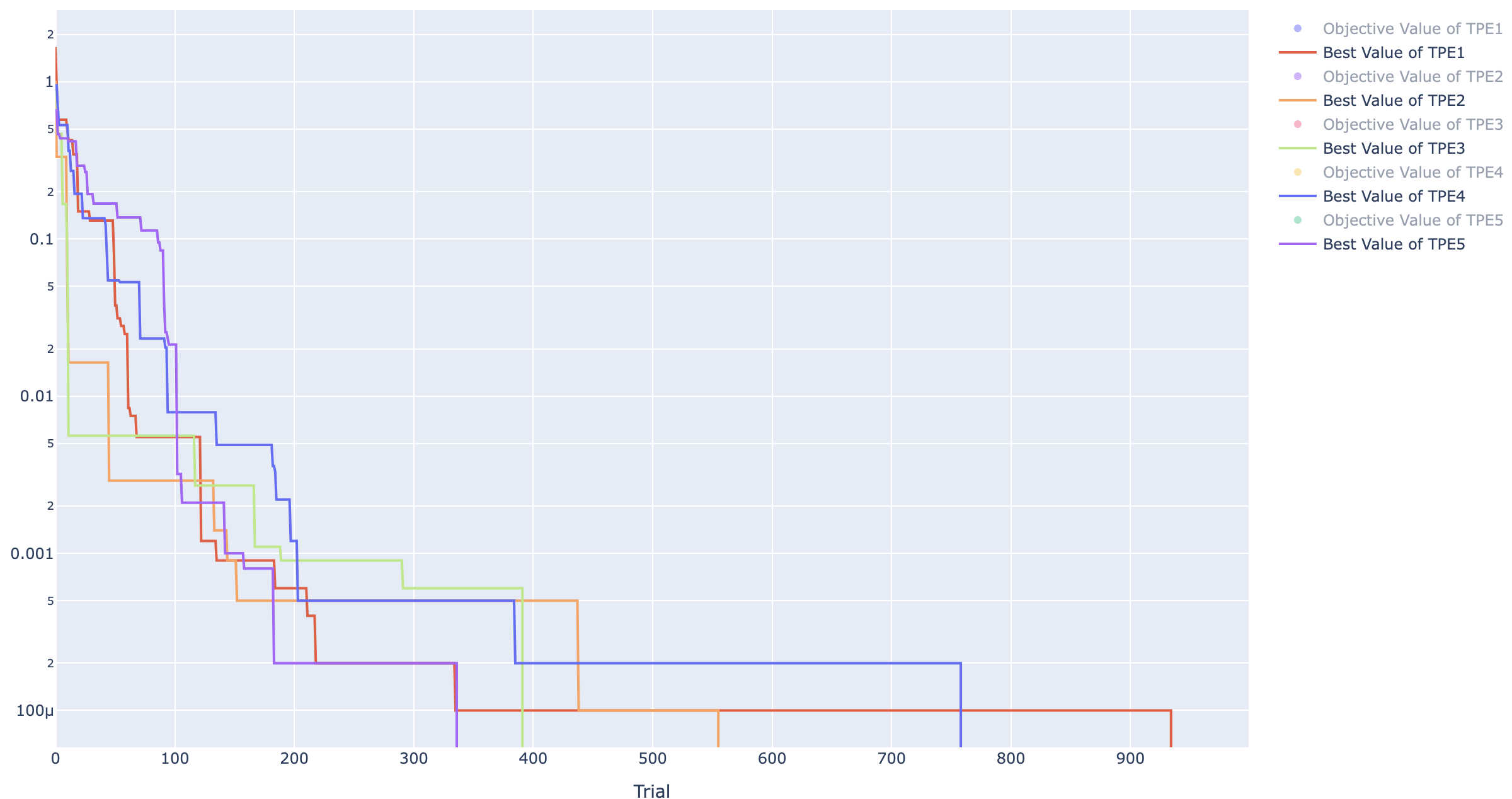
GA ヒストリー

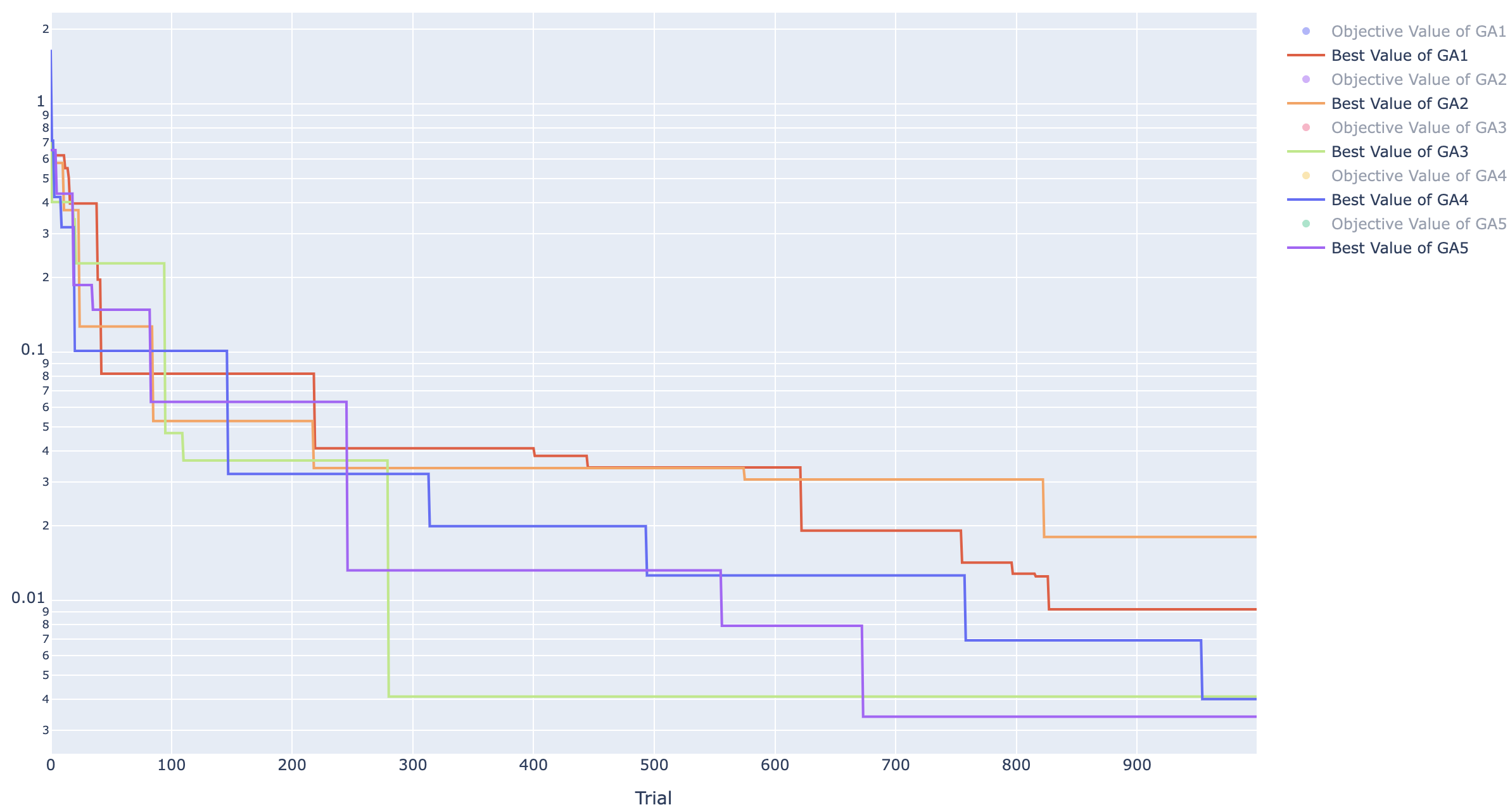
Random ヒストリー

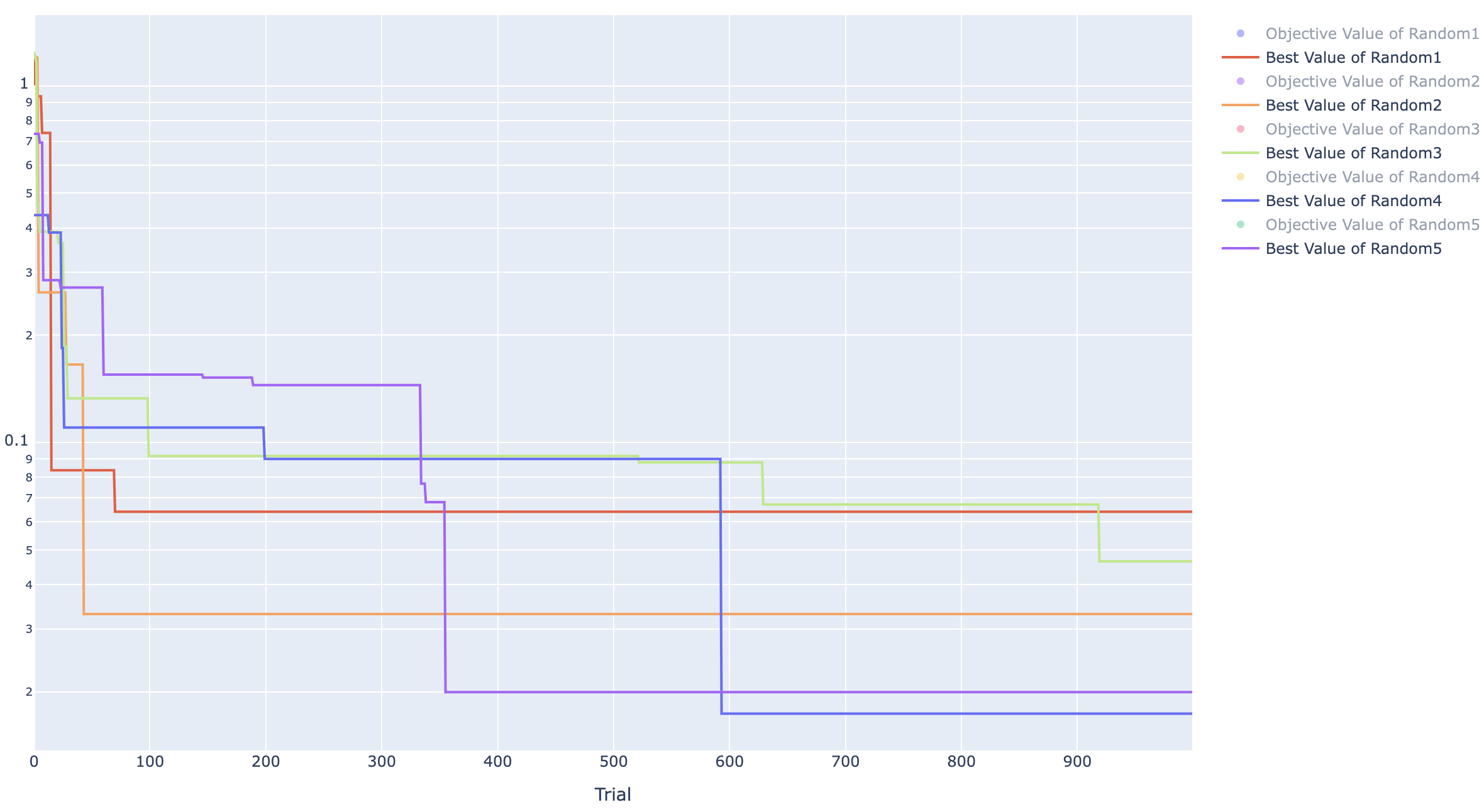
TPE はすべてのケースで 0 になりましたが GA は 0 になりませんでした。 ですが、100 試行のとき平均で 0.1238 だったのに対して、今回は 0.0077 になっており、かなり小さな値になっていることは確かです。

TPE が何試行目で 0 になったかも確認しました。 結果が以下です。 5回の平均で試行回数 596 で 0 になりました。

trial 1 2 3 4 5 minimum Average SD
TPE 935 556 392 759 337 337 595.8 224.4

単純ですが、やはり TPE も GA も試行回数を増やせばちゃんとより良い値になっていくことがわかりました。

最適化の設定を変えてみる

次に最適化手法の中での設定を変えてみます。 なお、ここでは最適化の設定の比較を行うため、内部で使用している疑似乱数のシード値を固定しています。 そのため設定の違いのみを考慮できるようにしています。

TPE 編

検討方針

TPE はデフォルトの設定でも 600 試行程度で 0 になることがわかったので、設定を変えてみてより少ない試行で 0 が得られる様になるか試してみます。 デフォルトでの設定は以下になっています。

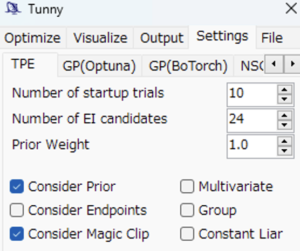
ここでは設定を変更する対象は以下の3つとします。 括弧中の値がデフォルトの値になります。

  • Number of startup trials (10)
  • Number of EI candidates (24)
  • Consider Endpoints (False)

TPE のようなベイズ最適化に分類される手法は代理モデルを作成してそれを使用して次に探索すべき点を決定します。 代理モデルの作成には初期に行うサンプリングの数に影響を受けます。 Tunny では Number of startup trials の数字が初期のサンプリング数となり、この数だけ最適化ではなくランダムにサンプリングされます。

獲得関数を評価する際のサンプリング数が Number of EI candidates になります。

それぞれ資料[1]によると以下のように記載されています。

  • Number of startup trialsは総試行数の1/10程度にすると良い
  • Number of EI candidates を増やすと獲得関数の評価の精度の向上が期待できる
  • 変数の両端を丁寧に調べたいときは Consider Endpoints にはチェックを入れると良い

良い設定の探索

ではそれぞれを変化させて1000試行を行った際の結果です。 表は横軸が Number of EI Candidates、縦軸が Number of startup trials の数になります。 「0 が得られた試行回数」の表は 0 にならなかったケースは一律で 1000 としています。

Consider Endpoints 最適化結果 0 が得られた試行回数
False file file
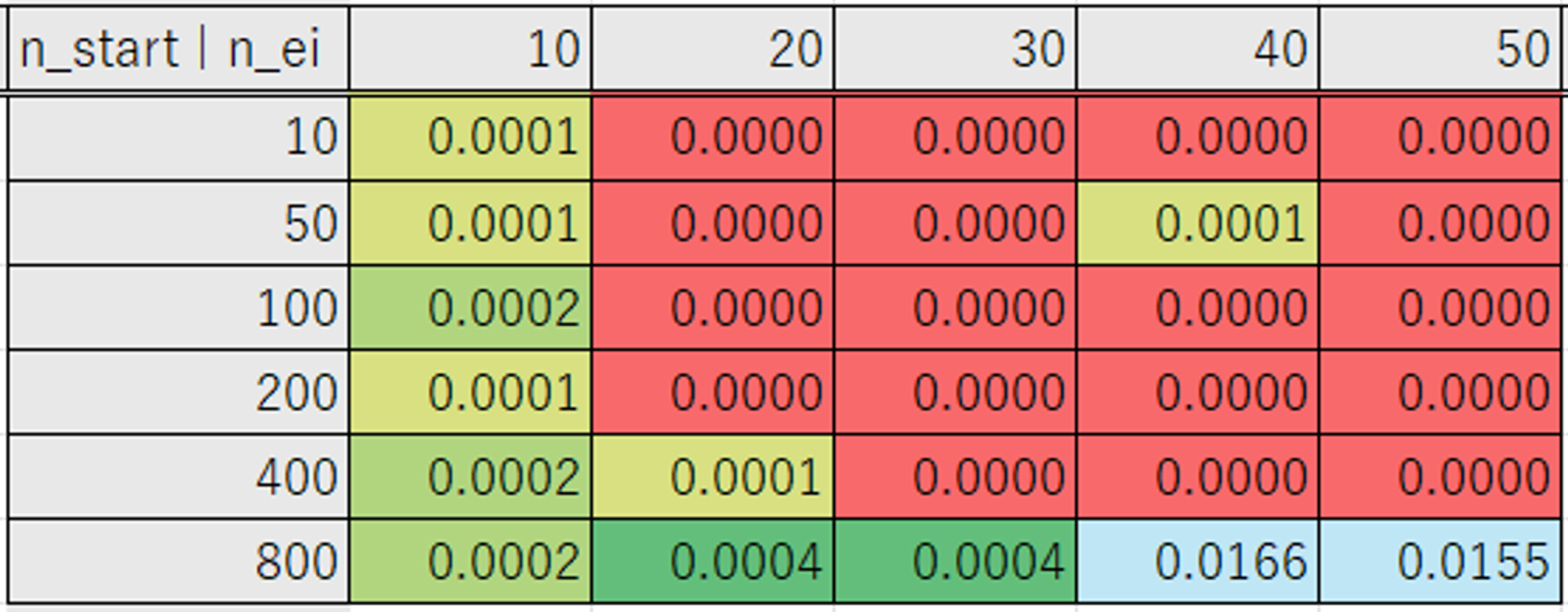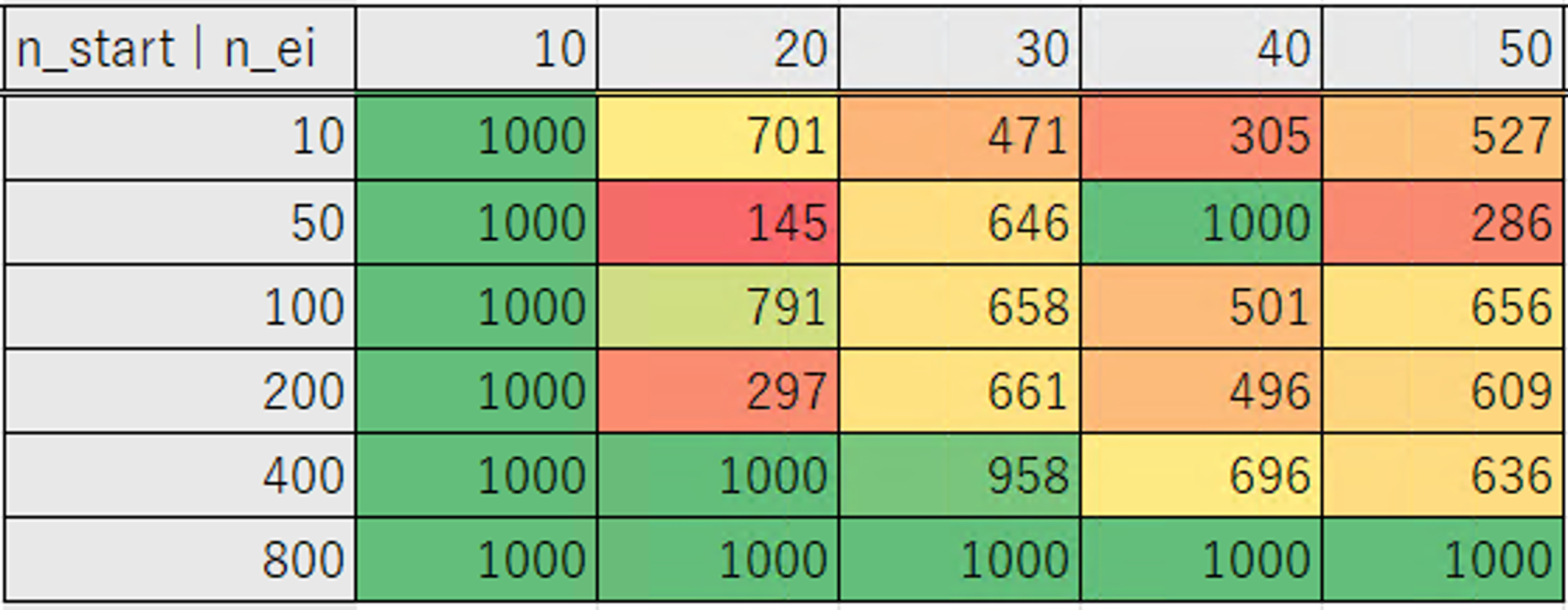True file file

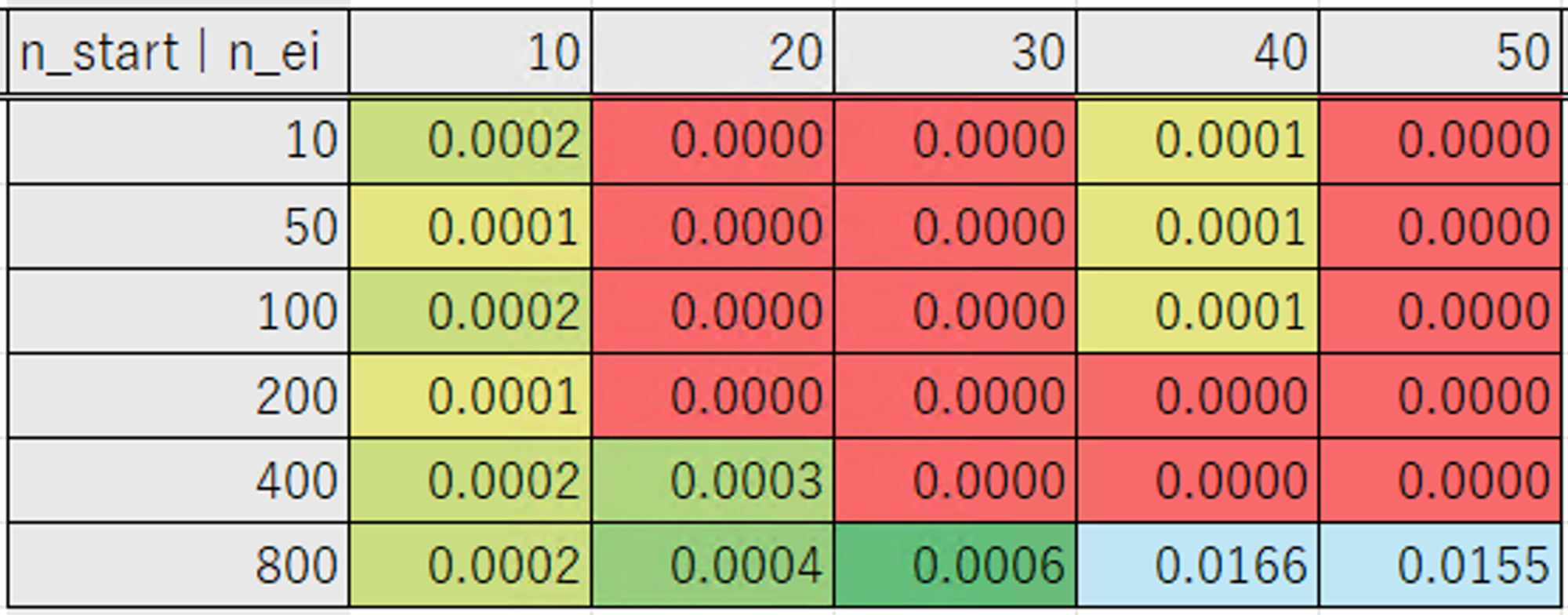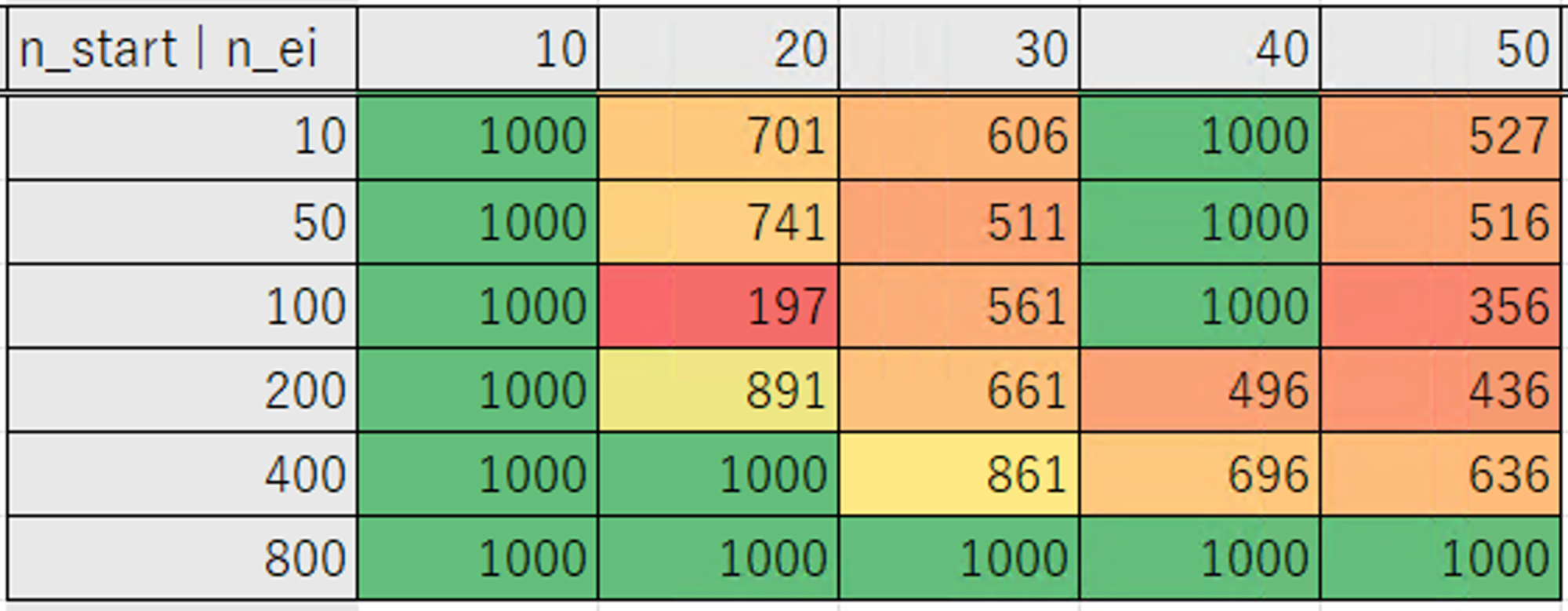なおデフォルトの設定では、597 試行目で 0 の値になりました。

上記で結果が良かった以下の組み合わせで、冒頭で最適化したときのようにシード値を固定しないで5回最適化を実行したときに、結果が良くなるか確認してみます。

case 1 case 2 case3
Number of startup trials 50 50 100
Number of EI candidates 30 50 50
Consider Endpoints True False True

Number of EI candidates が 20 のときに最も少ない試行回数で 0 になる結果が得られています。 ですが、設定によって 0 になるまでの試行回数のばらつきが大きいです。 そのため上記の設定の組み合わせの選択にあたって、ばらつきの少ない Number of EI candidates が 30 以上の結果から選択しました。

決定した設定での最適化

前節で決定した3つの設定のケースで最適化を行った結果が以下になりました。

すべて最適値は 0 になったので、0 になるまでにかかった試行回数のみをまとめています。

1 2 3 4 5 minimum Average SD
case 1 243 498 220 581 828 220 474 226
case 2 71 320 679 244 437 71 350 203
case 3 641 652 799 558 568 558 644 86
default 935 556 392 759 337 337 596 224

最適化のヒストリーは以下です。 対数表示のため、値が 0 になると枠外に線がでます。

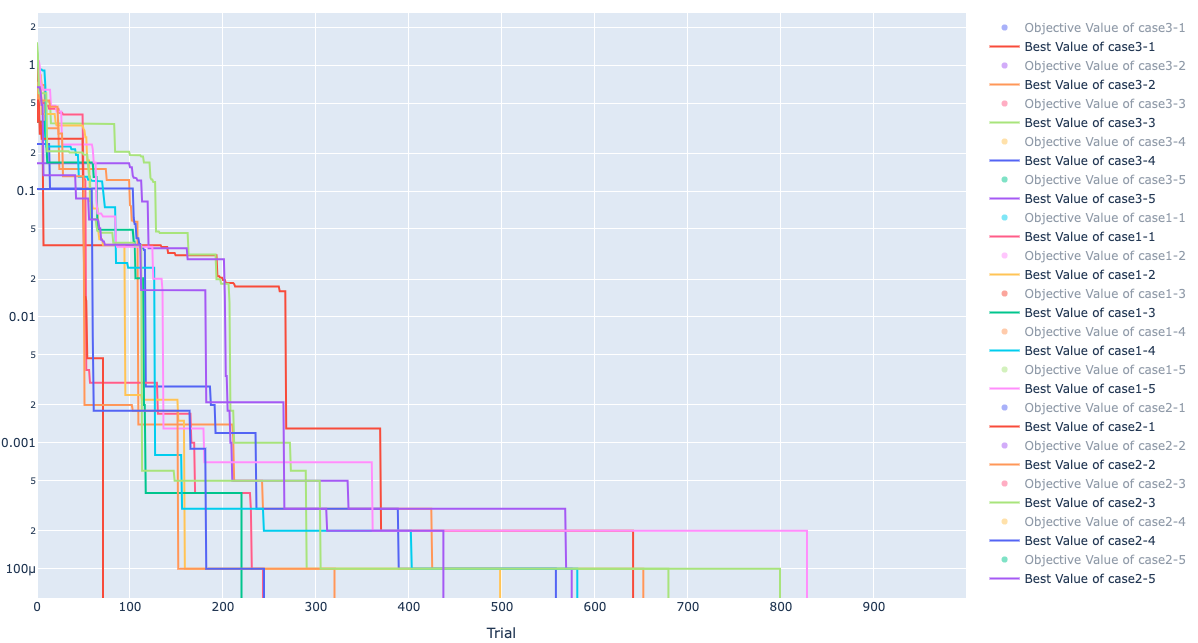
case 1, 2 はデフォルトでやった際に比べて 5 回の中の最小試行回数、平均試行回数が改善しています。 case 3 は最小試行回数、平均試行回数はデフォルトより少し悪くなっていますが、標準偏差が小さくなり、ばらつき少なく 0 の値が得られていました。

GA 編

では次に GA の設定を変更してみます。

もっとたくさんやってみる

1000試行でしたが、更に10倍して10000試行でどうなるか試してみた結果が以下です。 たくさんやることにより、段々と小さくはなっていますが、0 にはなりませんでした。

1 2 3 4 5 minimum Average SD
NSGAII 0.0011 0.0008 0.0005 0.0003 0.0015 0.0003 0.0008 0.0004

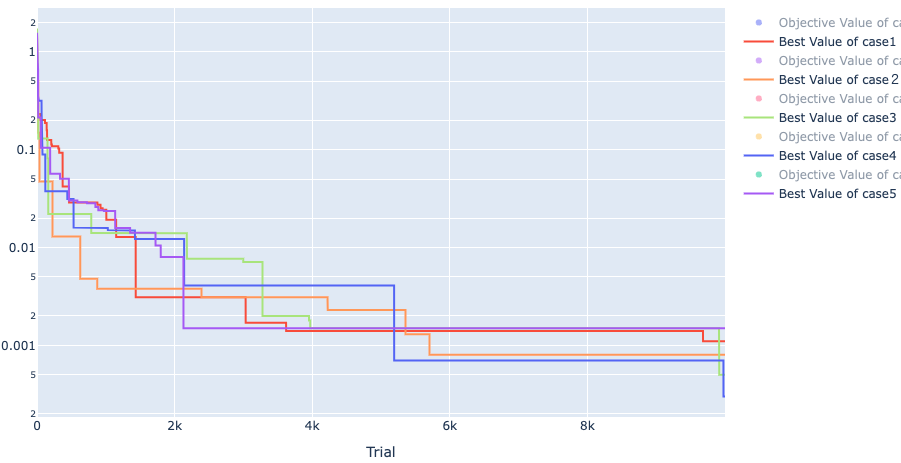
交叉方法を変える

他の手法と異なり、GA で 0 が得られないのは流石に設定が悪いと思われるので、設定を考えます。

GA では良い結果の親同士を交叉させ、より良い個体を探索していく手法なため、対象を交叉の手法にしぼり、設定を変えてみます。

Tunny では交叉の手法を以下の6つの種類から選ぶことができます。

  1. BLXAphaCrossover：ブレンド交叉
  2. SBXCrossover：疑似バイナリ交叉
  3. SPXCrossover：シンプレクス交叉
  4. UNDXCrossover：単峰正規分布交叉
  5. UniformCrossover：一様交叉（デフォルト設定）
  6. VSBXCrossover：修正疑似バイナリ交叉

デフォルトは一様交叉ですが、参考文献[2]より、変数の多い最適化の場合、一様交叉は比較的性能が悪いとされています。 そのため、この手法を変更することで結果の改善が期待できます。

では実際に変えて最適化してみたときの結果をまとめたものが以下になります。 各手法で5回最適化を行い、それぞれで同じ条件になるように疑似乱数のシード値は同じ値にしています。

最適化結果

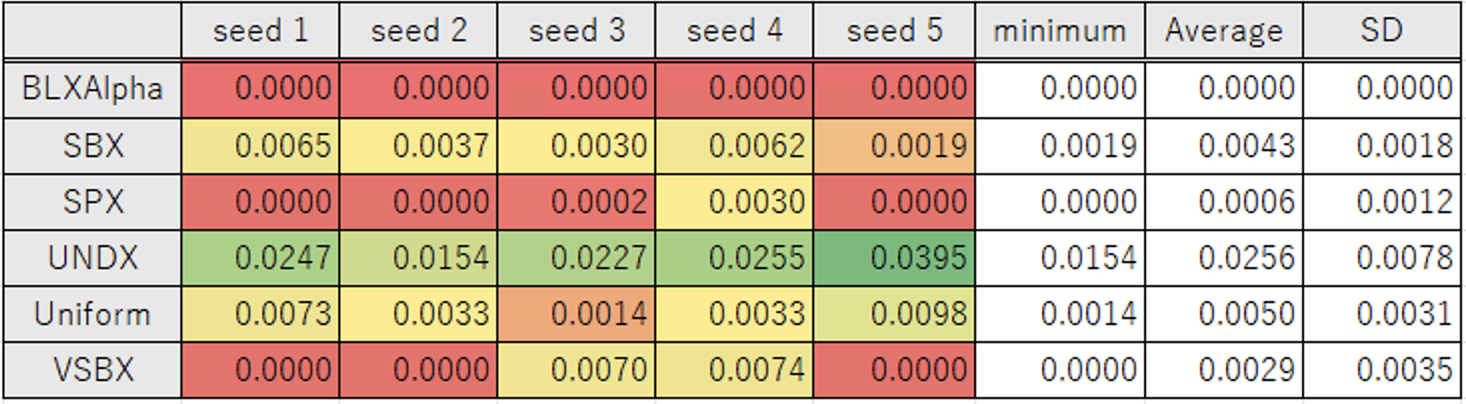
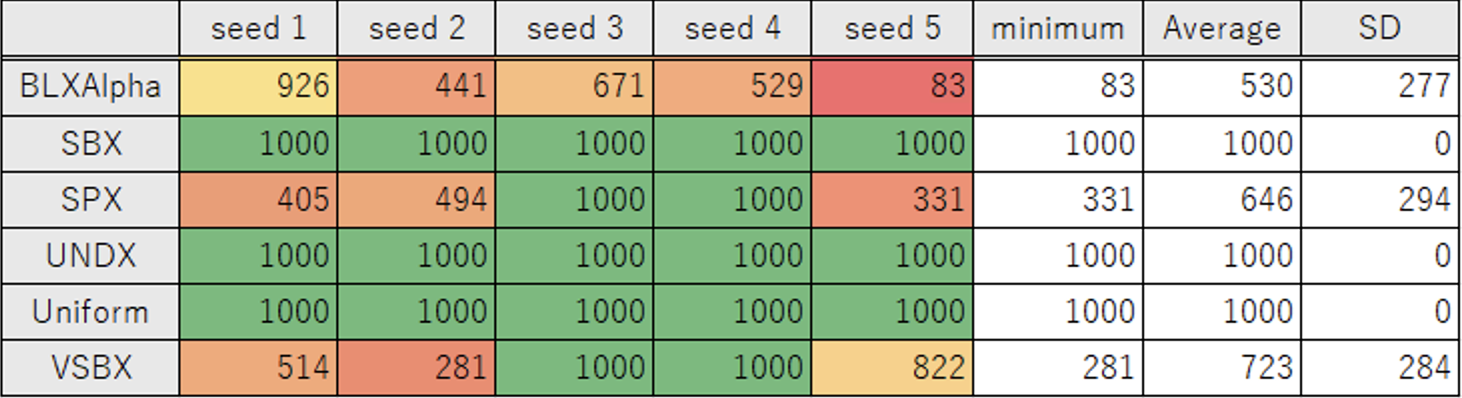
試行回数

Seed1 の各手法のヒストリー

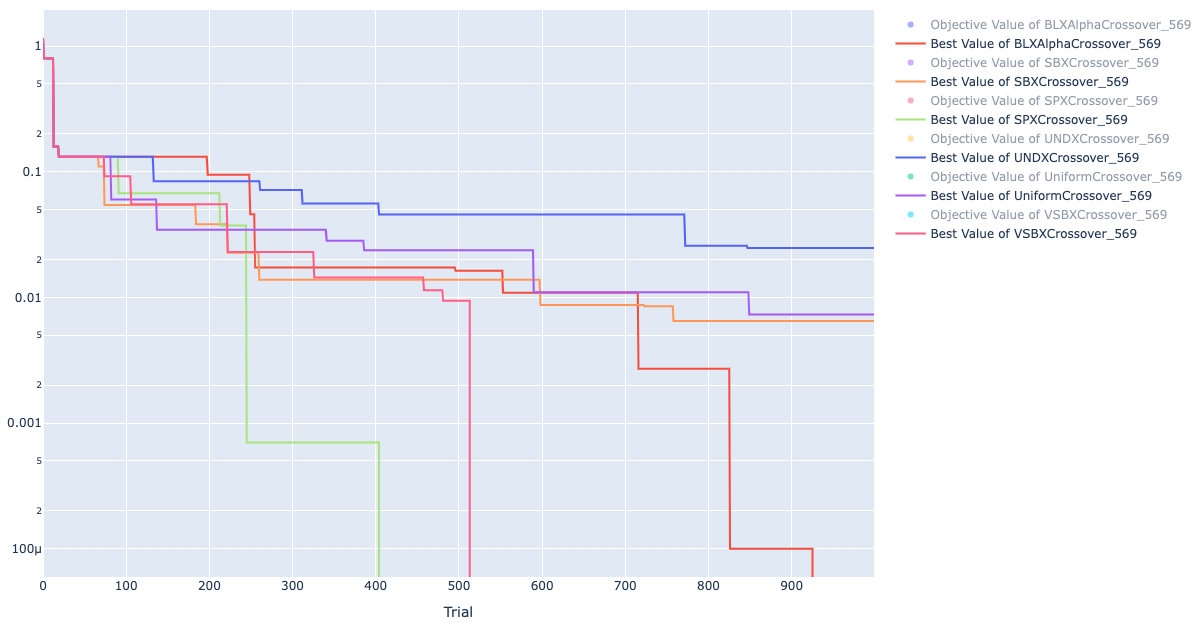
SBX, UNDX, Uniform の3つは 1 つも 0 になる結果が得られませんでしたが、BLXAlpha, SPX, VSBX は 0 を得ることができました。

特に BLXAlpha はすべてのケースかつ平均試行回数 530 で 0 が得られており、デフォルトの Uniform よりもかなり良い結果が得られました。

平均試行回数 530 は設定を調整した後の TPE での結果と同程度です。 この結果から、GA が手法として TPE に劣るというよりは、デフォルトの最適化設定が今回の最適化問題に対して適切ではなかったことがわかります。

補足

最終的に最も良かった手法である BLXAlpha(ブレンド交叉)は数値で表現された変数に対して有効な交叉手法です。

親個体の変数の組みに基づいて、その間の領域からランダムに子個体の変数の組を生成します。 子個体の変数の組は、親個体の変数の組の範囲に対して、パラメータα倍された領域の中から選択されます。

Tunny では \alpha = 0.5 を使用しています。

親個体をP_i(x, y) と表すとします。 P_1(0, 0)、P_2(10, 10) とすると\alpha = 0.5 のとき、この2つ親個体のブレンド交叉から作成される子個体は 2.5 \leqq x \leqq 7.5、2.5 \leqq y \leqq 7.5 の範囲で変数をとります。

まとめ

今回は Tunny を使って最適化の設定がどのように影響するかを確認していきました。 本記事で確認したのは Tunny の実装で、A+B という単純な目的関数の最適化での場合のみです。

実際の最適化問題を考えると、これ以外にも

  • 多目的最適化の場合は？
  • Tunny じゃなくて Wallacei や Galapagos を使った場合は？
  • もっと複雑な目的関数の場合は？
  • もっと変数の組み合わせが増えた場合は？
  • 制約条件を考慮した場合は？

など様々なケースが考えられ、それぞれでどのようなプラグイン、どのような設定、どのような手法、で最適化したら高速に良い結果が得られるかは変わってきます。

自分の今の設定でちゃんと必要とする精度での最適化が行われているかは常に考えながら最適化しましょう。

本記事を読んで、各設定の意味をより詳細に知りたくなった場合は、記事中の資料として参照している Tunny が最適化ライブラリとして使用している Optuna の開発者によって書かれた本[1]を一読することをおすすめします。

最適化を最適化して、よりよい最適化ライフを過ごしましょう。

参考文献

Writer

チーフエンジニア / 一級建築士

Chief Engineer / First-class registered architect

夏目大彰Hiroaki Natsume Hiroaki Natsume

早稲田大学大学院 創造理工学研究科 建築学専攻 卒業（修士）。建築の組織設計事務所にて教育施設や免震建物、超高層ビルなどの構造設計に従事。業務の傍らコンピュテーショナルな構造設計の普及のためのコミュニティ活動や支援ツールの開発を行う。2020年よりNature Architectsに参画。
一級建築士。

採用インタビューはこちら

Graduated from the Graduate School of Creative Science and Engineering, Waseda University (Master of Engineering). He has been engaged in structural design of educational facilities, seismic isolation buildings, and skyscrapers, an architectural design firm. In addition to his work, he is involved in community activities and the development of support tools to promote the spread of computational structural design. He joined Nature Architects in 2020.
First-class registered architect.

Hiroaki Natsume

Related Topics

Up Next

MOEA/Dの紹介と多目的最適化の比較の一例

MOEA/Dの紹介と多目的最適化の比較の一例

Introduction to MOEA/D and an Example Comparison of Multi-Objective Optimization Methods

最適化問題の解決に広く使われているOptunaが、最近バージョン4にアップデートされ、新たにOptunaHubという機能が追加されました。これを機に、私たちは多目的最適化アルゴリズム「MOEA/D」の実装をOptunaHubを通じて公開しました。 本記事では、MOEA/Dの特徴と、他の最適化手法との比較結果の一例を紹介します。進化型多目的最適化に興味がある方、より効率的な最適化手法を探している方は参考にしてください。

Optuna, widely used for solving optimization problems, has recently been updated to version 4, introducing a new feature called OptunaHub. Taking this opportunity, we have published an implementation of the multi-objective optimization algorithm "MOEA/D" through OptunaHub. In this article, we introduce the characteristics of MOEA/D and present an example comparison with other optimization methods. Those interested in evolutionary multi-objective optimization or seeking more efficient optimization techniques may find this article useful.

夏目大彰

Hiroaki Natsume

2024,09,20 2024,09,20
CFDにおけるFEMとFVM

CFDにおけるFEMとFVM

FEM and FVM in CFD

構造解析では有限要素法、流体解析では有限体積法。偏微分方程式を離散的に解く手法という意味ではどちらも共通しているのに、構造と流体ではなぜ違う手法が一般的なのでしょうか？本記事では、流体解析における有限要素法と有限体積法を比較して「なぜCFDでは有限体積法が一般的になったか」の理由を垣間見ていきます。

Structural analysis uses the finite element method, while fluid analysis uses the finite volume method. Why are different methods commonly used for structure and fluid analysis, even though both are the same in the sense that they are methods for solving partial differential equations discretely? In this article, we compare the finite element method and the finite volume method in fluid analysis and give a glimpse into the reason “why the finite volume method became common in CFD."

古澤善克

Yoshikatsu Furusawa

2024,08,23 2024,08,23