はじめに
弊社ではブラックボックス最適化問題を扱う際にPythonの最適化フレームワークであるOptuna[1]、及びOptunaを3DCAD上での形状探索に利用するプラグインTunny[2]を使うことがよくあります。
Optunaは先日バージョン4になりました。
その中で、Optunaに対して機能を追加した実装を公開できるOptunaHubという機能のハブとなるサービスがリリースされました。
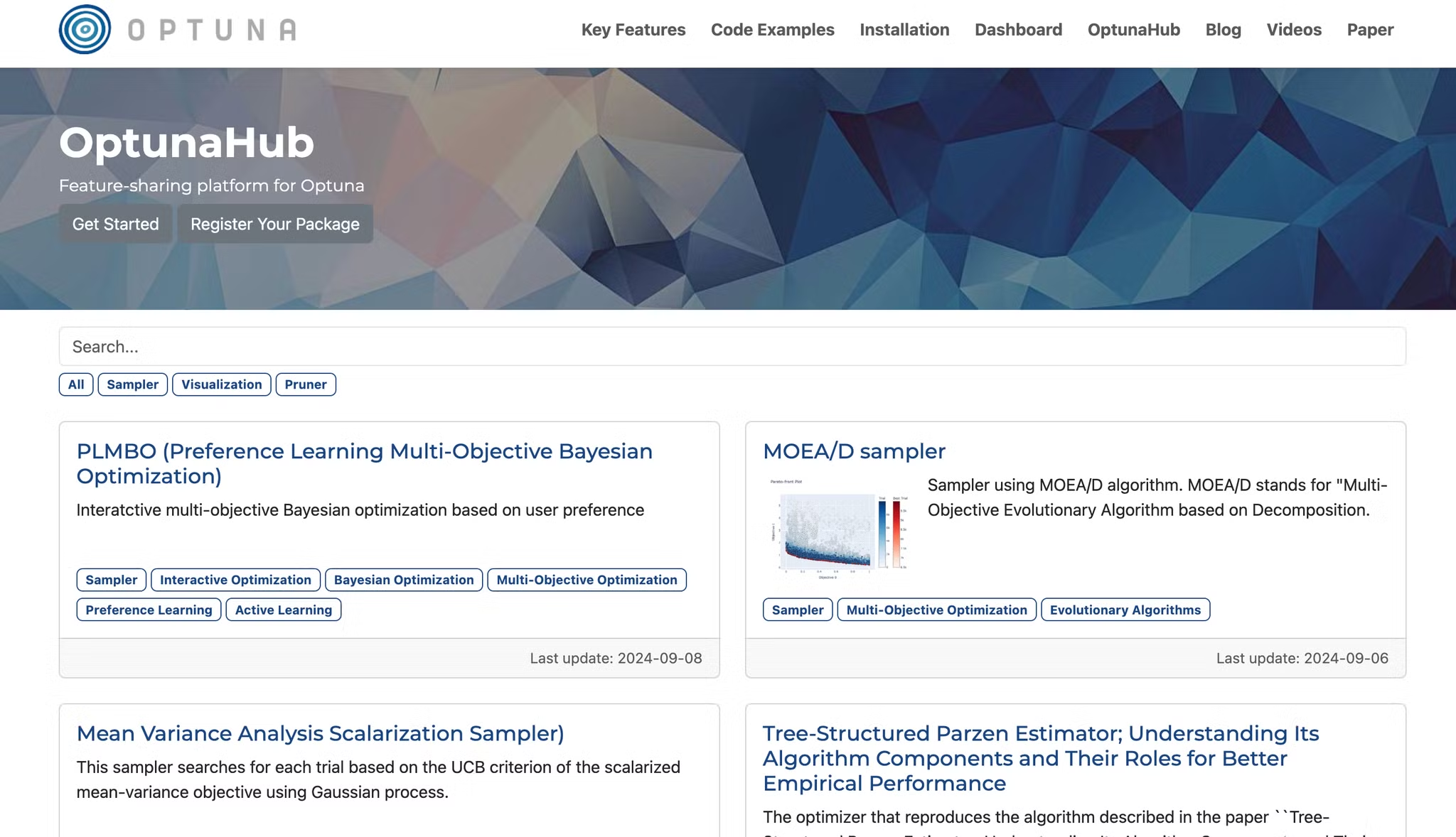
これまでOptunaは単一目的最適化が得意なサンプラーは多く実装されてきました。
一方で弊社でよく行う多目的最適化に特化したサンプラーは多くは実装されていませんでした。
そのため、弊社での多目的最適化の選択肢の増加と効率の向上及びOptunaコミュニティーへの貢献のために、多目的最適化向けのアルゴリズム”MOEA/D”を実装し、OptunaHubを通じて公開しました。
https://hub.optuna.org/samplers/moead/
今回は実装したMOEA/Dの特徴と他の手法での多目的最適化結果との比較の一例を紹介します。
MOEA/Dの概要
MOEA/Dは「A Multiobjective Evolutionary Algorithm Based on Decomposition」の略で、進化型多目的最適化(EMO: Evolutionary Multiobjective Optimization)の一種になります。
多目的最適化の文脈にて参照されることの多い手法であり、発展型の手法も多く提案されています。
論文[3]を元に簡単にアルゴリズムを紹介します。
特徴
名前に Decomposition(分解)が含まれるように、MOEA/Dは多目的最適化問題を複数の単一目的最適化問題に分解することできれいなパレートフロントを得ようとする手法です。
分解された各最適化問題は部分問題(subproblem)と呼ばれます。
多目的最適化問題を分解する際には、各目的関数に対する重みベクトルを使ってスカラー化する手法(スカラー化関数)が使われます。
重みベクトルは1つの世代に含まれる個体の数と同じだけ生成され、最初の世代では各個体にランダムに1つの重みベクトルに割り当てられ1つの部分問題となります。
スカラー化関数
論文中では以下の3つのスカラー化関数が掲載されていますが、OptunaHubで公開した実装では最初の2つのみが実装されています。
- Weight Sum
- Tchebycheff
- Penalty-based Boundary Intersection (PBI)
上記の中では、Tchebycheffアプローチがデフォルトでよく使われるスカラー化関数になります。
Tchebycheffアプローチの計算は以下です。
最小化問題の場合は、重みベクトルによって重み付けされたチェビシェフ距離 g が最小になるように各部分問題が解かれていきます。
\lambda は重みベクトル、f(x)は目的関数、z^* は参照点です。
g= \max \{ \lambda_i | f_i(x) - z^*_i | \}
例えば重みベクトル(1, 0) が割り当てられた部分問題は目的関数f1のみを扱い、重みベクトル(0.5, 0.5)が割り当てられた部分問題はf1とf2を等しい重みで扱う問題となります。
子個体の作成
部分問題での子個体の作成には、部分問題の近傍の個体を選択し、GA などと同様にそれらに対して交叉や突然変異を行います。
この部分は Optuna の NSGAII と同様の実装になっており、既に Optuna で実装されている各種交叉の手法を用いることができます。
ここで部分問題の近傍とは、対象に割り当てられている重みベクトルに対するユークリッド距離の近い重みベクトルをもつ部分問題に属する個体になります。
いくつの近傍の部分問題に属する個体を親個体に含めるかのパラメータは、論文中では T 、OptunaHubの実装では n_neighbors という引数になっています。
T が大きいほどより広い範囲に含まれる親個体の中から子個体が生成されるため、より広い範囲での探索が行われ、小さいほど狭い範囲での探索が行われるため、MOEA/Dの性能を決める重要な変数になっています。
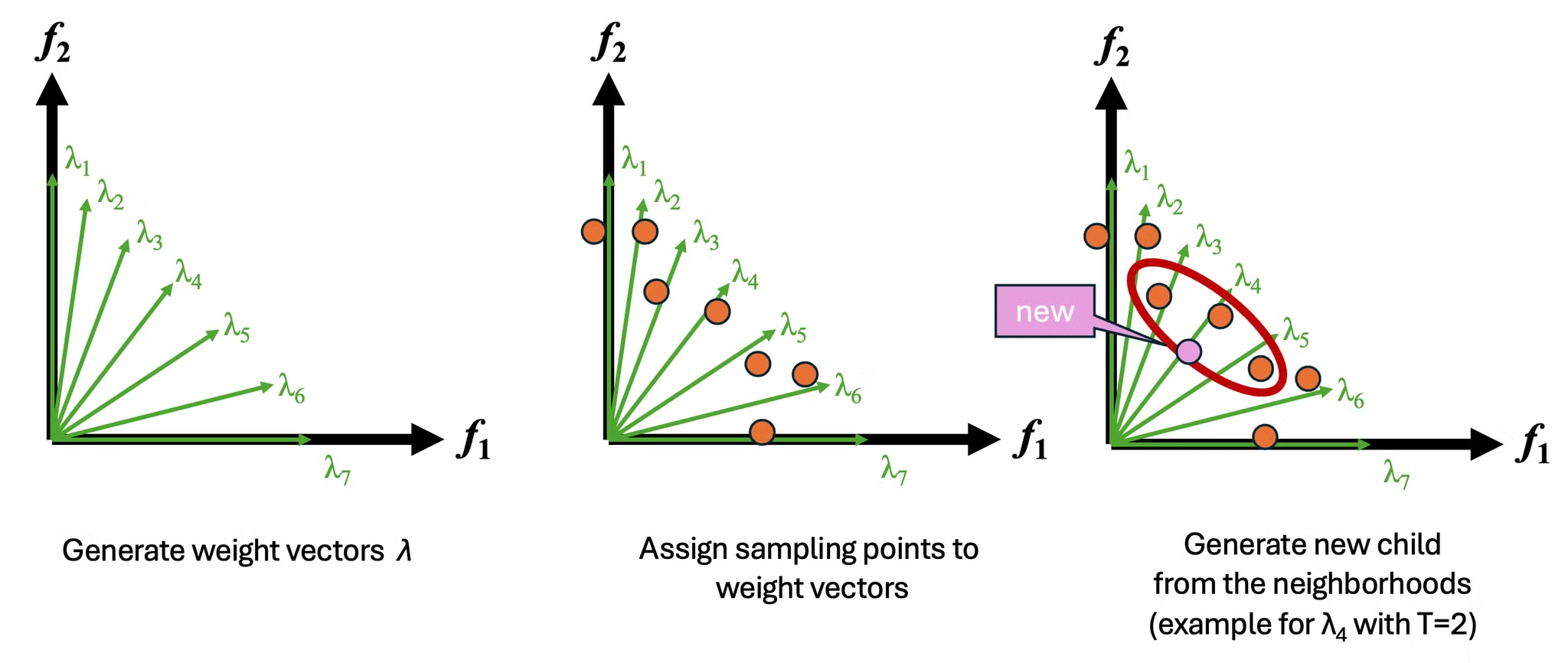
重みベクトル
重みベクトルの一様性もMOEA/Dでは重要になります。
上記の図では2次元に一様に重みベクトルが分布していますが、目的関数の次元が高次元になるほど、適度な密度で一様にベクトル分布させることが難しくなっていきます。
実装では、2目的の場合は均等分割としていますが、3目的以上の場合は準モンテカルロを使った超一様サンプリングによって生成しています。
そのため3次元を超える場合の重みベクトルについてはより一様にするための改善の余地があります。
より一様に分布させる手法として例えば[4]があげられます。
目的関数が多い場合は1世代の個体数を増やし、重みベクトルがあまり疎にならないように注意してください。
比較
実際に使った場合、どのような結果になるのか、Optunaを使って確認してみます。
比較対象として、以下の5つの手法を使用しました。各手法で用いるランダムのシード値は同じ値を使用しています。
| 手法 |
選択理由 |
| MOEA/D |
- |
| NSGAII |
比較のベースとなるアルゴリズム |
| NSGAIII |
NSGAIIの多目的最適化への対応を強化したアルゴリズム |
| TPE |
ベイズ最適化系の多目的最適化 |
| Random |
比較のため |
結果の比較については最終的なパレートフロント形状だけでなく、ハイパーボリュームの変化、最適化の実行時間も合わせて確認しました。
目的関数
目的関数には多目的最適化のベンチマークとしてよく使われる ZDT1[5] を用いました。
この関数は以下の式で表されるf1, f2を目的関数とする2目的最適化問題に使用される関数です。
今回は n=30 として30変数の問題として使用しています。
f_1(x) = x_1\\
g(x)=1 + \frac{9}{n-1}\sum^n_{i=2}x_i\\
f_2(x) = 1-\sqrt{f_1/g}\\
0 \leq x_i \leq 1,i=1,...,n
最適化結果
パレートフロント図
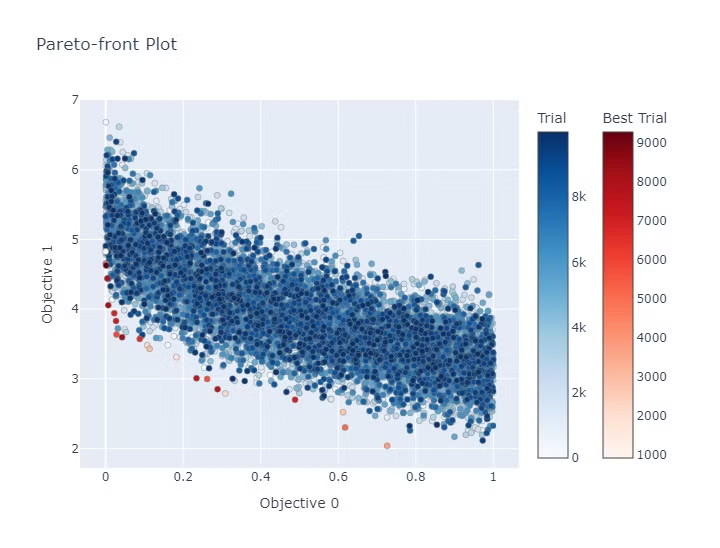
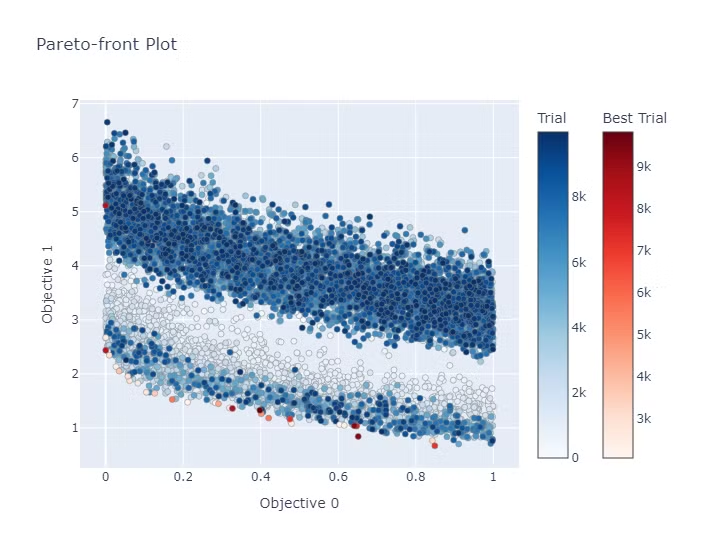
最適化を実施した結果のパレートフロント図は以下になります。
色が濃い点ほど後の試行の結果になり赤い点がパレードフロントの個体になります。
| Random |
TPE |
 |
 |
| NAGA II |
NSGA III |
 |
 |
| MOEA/D |
|
 |
|
TPEは色の濃さを見ると早い段階でパレートフロントになる個体を見つけています。
一方で、一定以上の試行になるとランダムとあまり変わらない分布になっています。
これは後に記載するHypervolumeのグラフからも読み取れます。
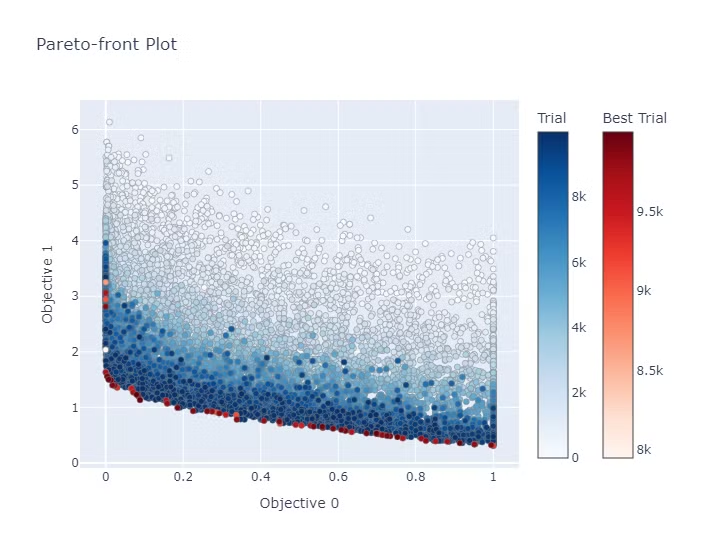
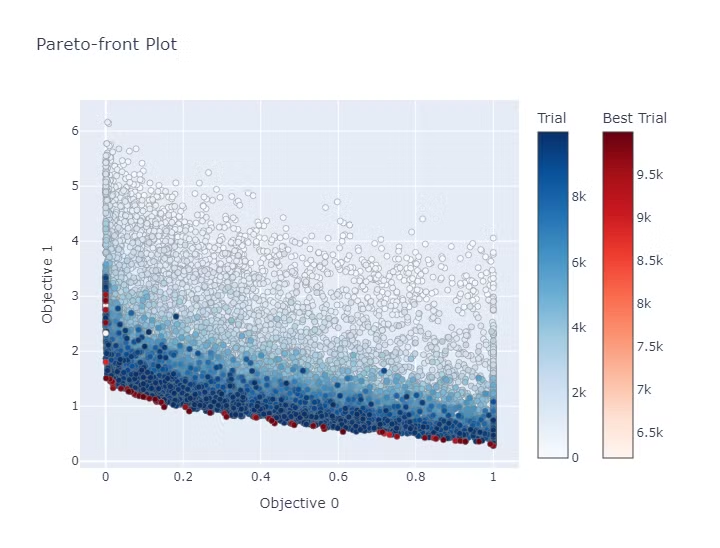
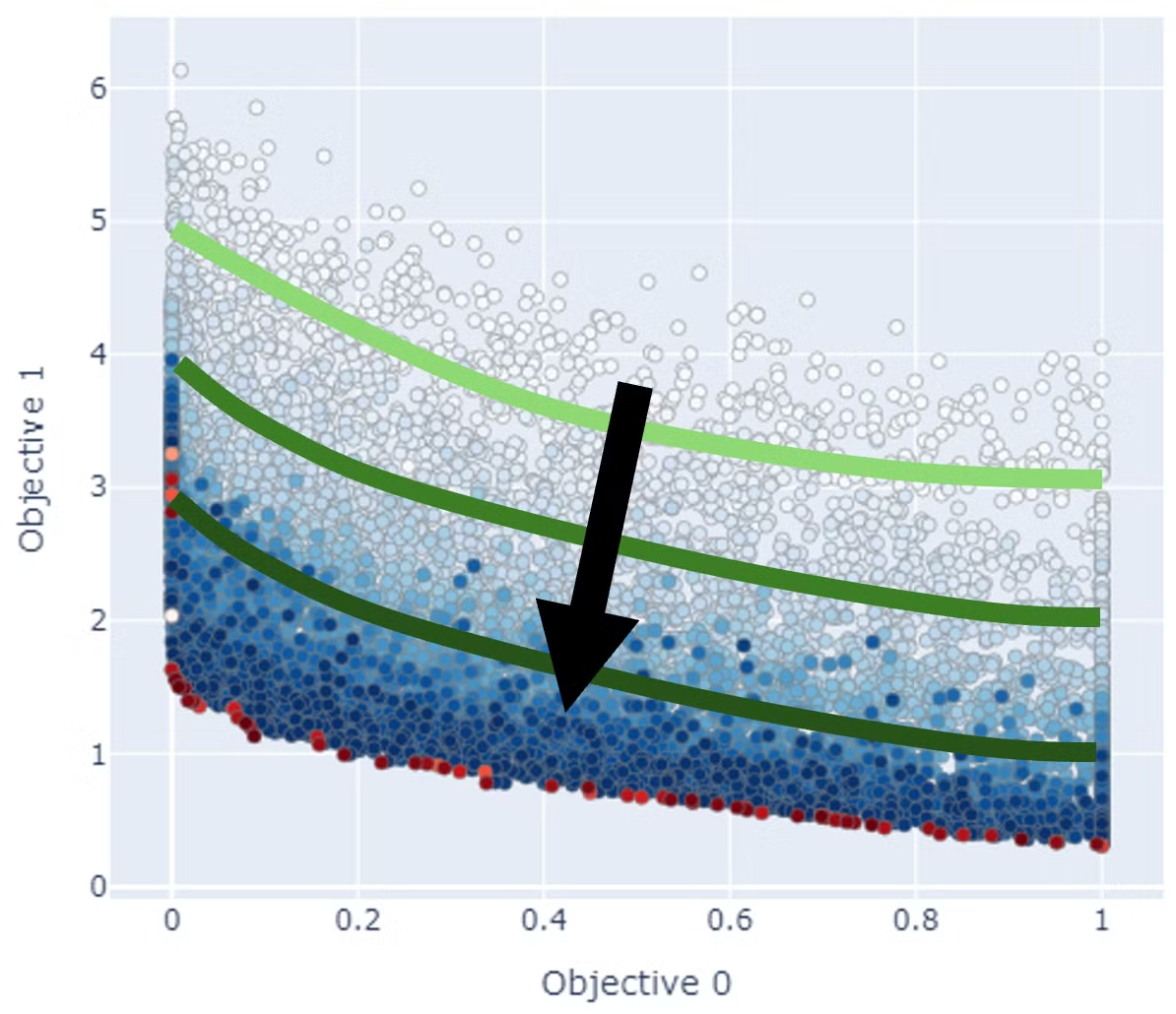
NSGAII、NSGAIIIは各世代ごとにパレートフロントにいる個体を交叉させることでより良い個体を発見していく手法です。
結果も上から下に点の濃さのグラデーションのようになっており、世代を重ねるごとにじわじわとパレートフロントが改善されていることがわかります。
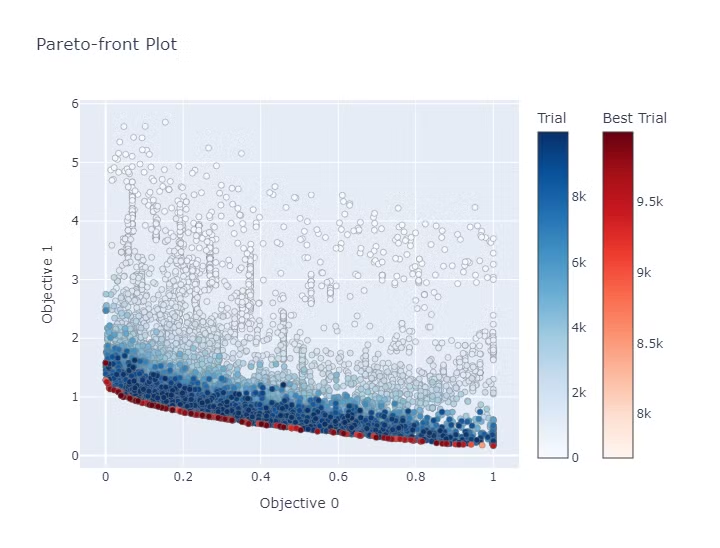
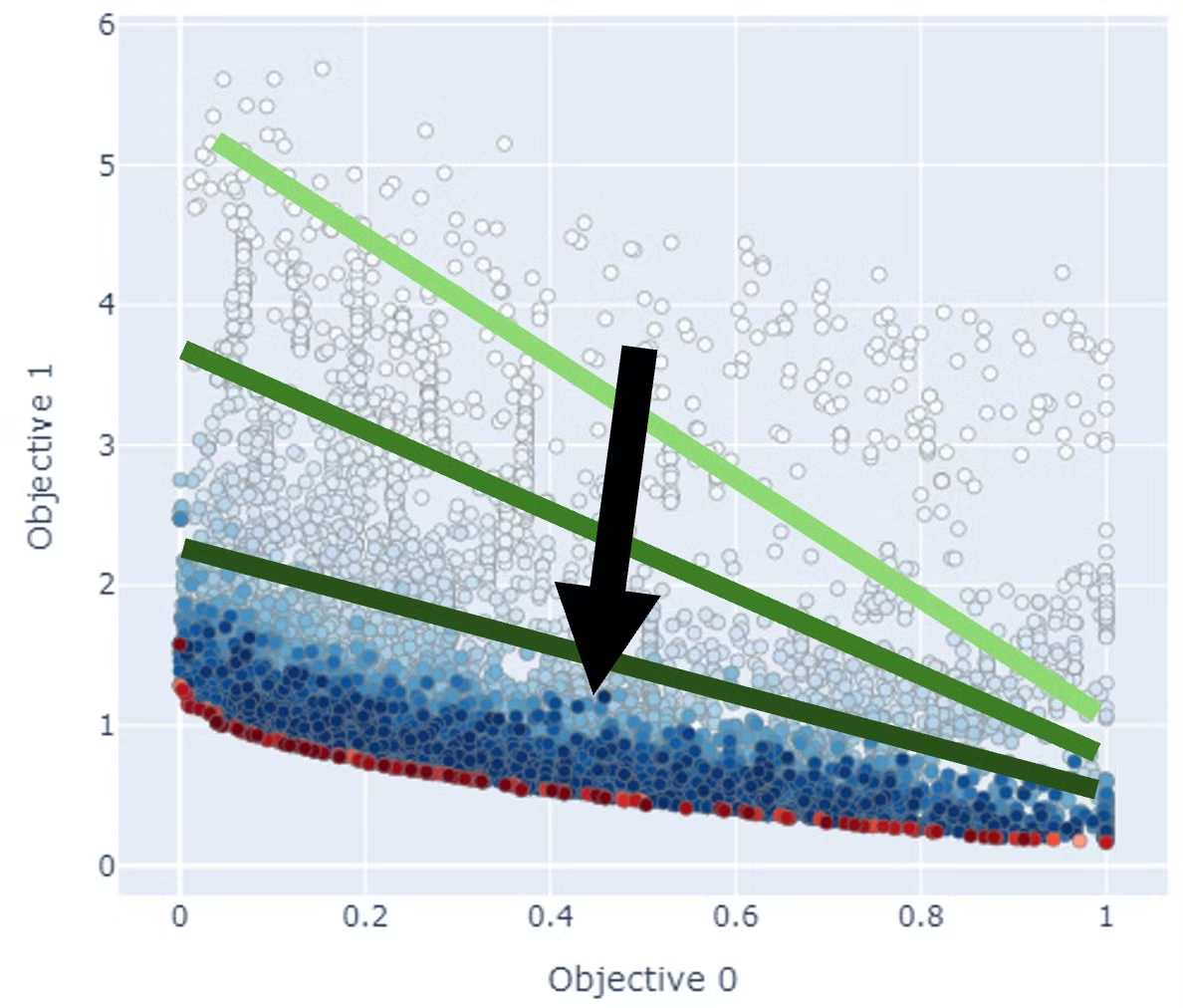
MOEA/Dでは重み付けされたベクトルを使った部分問題で解いていくため、NSGAとは異なり重みベクトルに応じた個体の分布があることが見て取れます。
| NSGA |
MOEA/D |
 |
 |
パレートフロント個体の確認
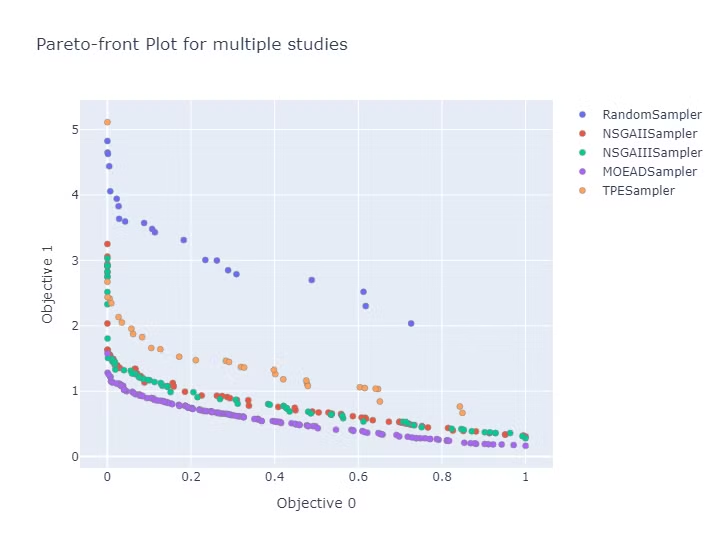
各手法の最終的なパレートフロントの個体のみをプロットした図は以下になります。
すべての手法でランダムを大きく上回っています。
NSGAIIとNSGAIIIは似たようなパレートフロントとなりました。
本例の設定ではMOEA/Dが最も良いパレートフロントが得られています。
Hypervolume
横軸に試行回数を取った Hypervolume の変化は以下になります。
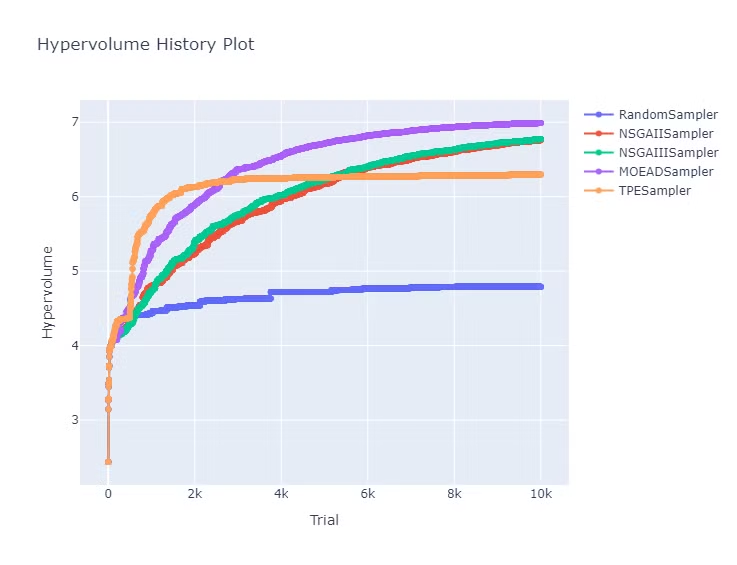
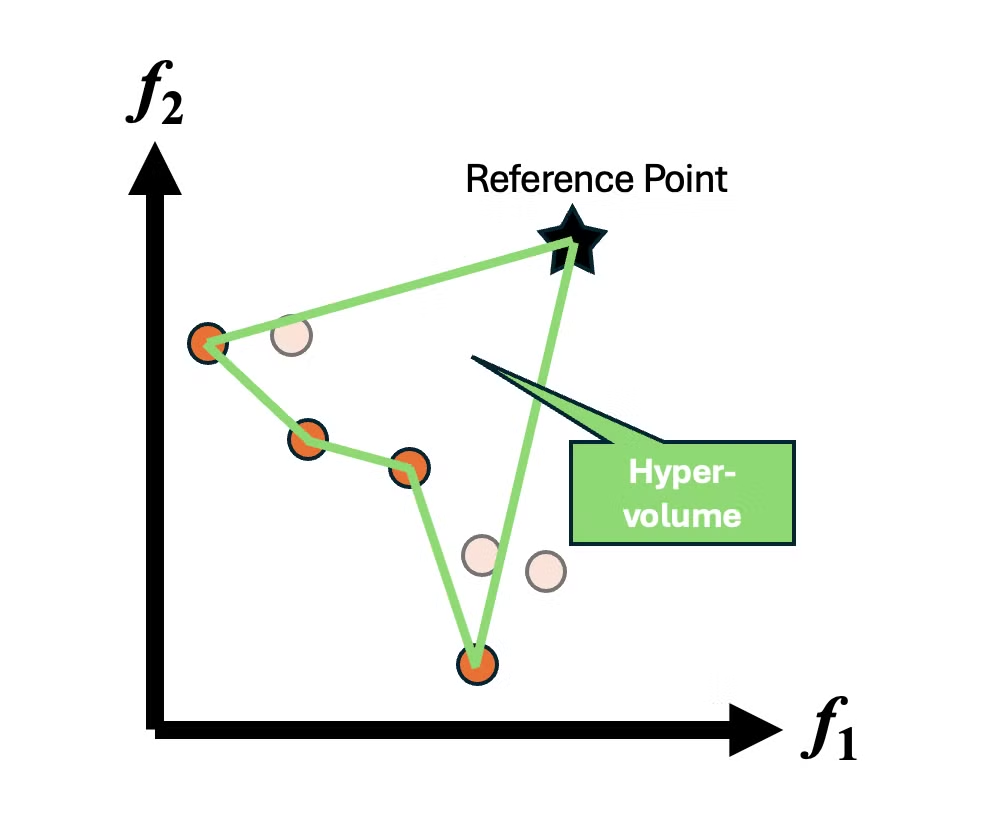
Hypervolume は多目的最適化を評価する指標の一つです。
特定の参照点とパレートフロントの点がなす図形の面積(3次元では体積、4次元以上では超体積)がHypervolume になります。
この値が大きいほどよりよいパレートフロントが得られていることの指標になります。
一定の試行以降ではどの手法もランダムを上回る Hypervolume となっています。
TPE は最初の 500 試行をランダムにサンプリングし、代理モデルを作成した後に TPE を使ったサンプリングをしています。
そのため 500 試行付近を境に、Hypervolume が急激に増える箇所があることがわかります。
一方で 2500 試行あたりから Hypervolume が頭打ちになっています。
頭打ちになったことについては、設定に改善代があると思われますが、多くの試行を行うことには向かず限られた試行の中で良い結果を探索できるベイズ最適化の特徴が出ている結果だと思われます。
MOEA/D は今回の比較の中では安定して良い Hypervolume の結果が得られています。
計算時間
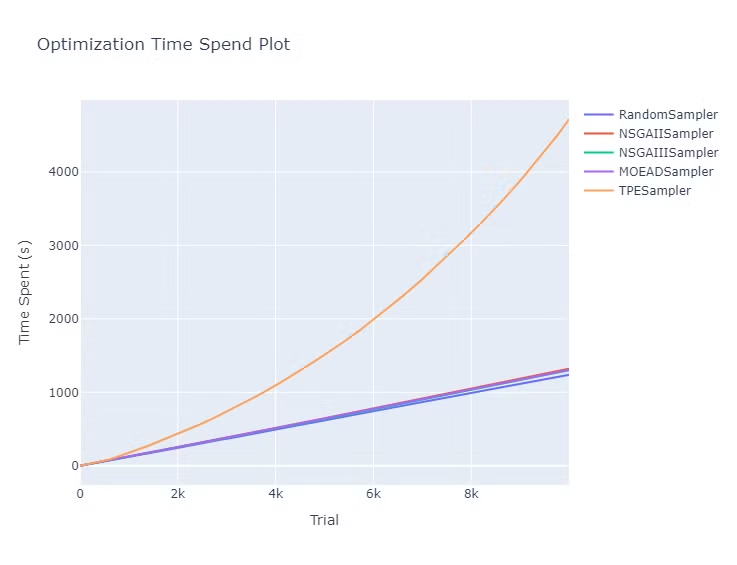
計算時間の図は以下になります。
TPE は試行回数に対して指数関数的に時間が伸びていますが、それ以外の手法は線形で時間が増加しています。
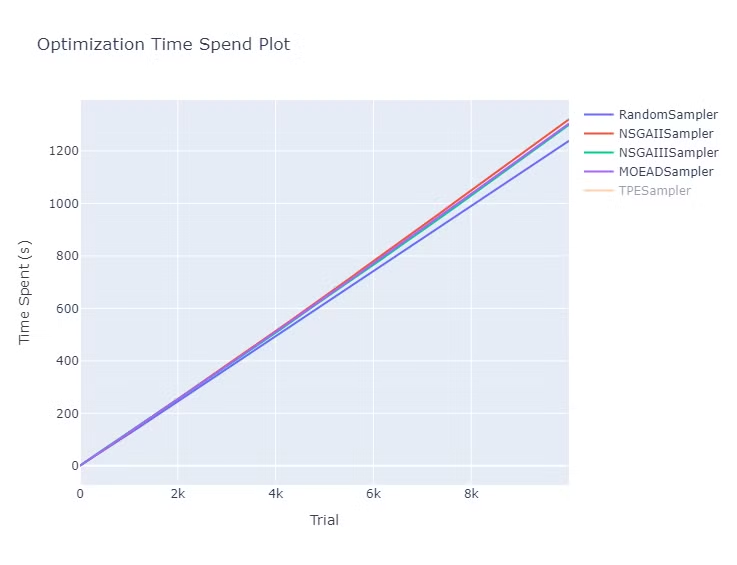
右側の図は TPE を除いた計算時間の図です。NSGA や MOEA/D は Random よりは時間がかかっていますが、ほぼ同じ傾向になっています。
| 全て |
TPEを除く |
 |
 |
Hypervolume の結果及び計算時間を見比べると、この設定においては TPE は 1000 試行程度であれば、他の手法に比べ最適化に費やす時間あたり最も大きな Hypervolume が得られています。
一方でそれ以降であれば他の手法のほうが良い結果が得られています。
この結果は Optunaの公式ドキュメントにある TPE の Recommended budgets (#trials) が100-1000であることに一致します。
なお、後半の計算時間を除く2つの図は Optuna 本体には実装されていませんでしたが、OptunaHub で公開されているプロットを使用しています。
まとめ
今回は MOEA/D を実装したことから、MOEA/D の良さが出るような結果を紹介しました。
問題や設定によって各手法での最適化結果の優劣は変わるため、色々試行錯誤しながら最適化にチャレンジしてみてください。
本記事で紹介した進化型多目的最適化に興味がある方は、例えば”進化型多目的最適化の現状と課題”[6]にはこのような多目的最適化について時系列でまとめられているので、参照してください。
MOEA/Dはメタヒューリスティクスな手法の中で進化ベースのアルゴリズムに分類されます。
他には物理ベース(例:焼きなまし法)や群ベース(例:粒子群衆最適化)などに分類される様々な手法があります。
このように最適化は様々な手法があり、それぞれに一長一短があります。
多くは既存の最適化ライブラリ[7],[8]や商用ソフトに実装されており、使う上で必ずしも自身で実装する必要がない場合がほとんどです。
ですが、実際に手を動かして実装してみたり、挙動を比較してわかることも多くあります。
ただ使うだけではなく、こういった試みも是非チャレンジしてみてください。
注)MOEA/Dの実装についてはMITライセンスでOptunaHubに公開しています。ライセンスを理解したうえで利用お願いいたします。
参考文献
[1]:Akiba, Takuya and Sano, Shotaro et al., Optuna: A Next-generation Hyperparameter Optimization Framework, The 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2623--2631, 2019
[2]:Natsume, H. (2024). Tunny, The Grasshopper optimization tool (Version 0.12.0) [Computer software]. https://github.com/hrntsm/Tunny
[3]:Q. Zhang and H. Li, MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition, in IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712-731, Dec. 2007
[4]:Tomoaki Takagi, Keiki Takadama, and Hiroyuki Sato. 2020. Incremental lattice design of weight vector set. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion (GECCO '20). Association for Computing Machinery, New York, NY, USA, 1486–1494.
[5] : Eckart Zitzler, Kalyanmoy Deb, and Lothar Thiele. Comparison of multiobjective evolutionary algorithms: empirical results. Evolutionary Computation, 8(2):173–195, 2000
[6]:佐藤寛之, 石渕久生, “進化型多数目的最適化の現状と課題”, オペレーションズリサーチ2017年3月号
[7]:J. Blank and K. Deb, pymoo: Multi-Objective Optimization in Python, in IEEE Access, vol. 8, pp. 89497-89509, 2020
[8]:Juan J. Durillo, Antonio J. Nebro, jMetal: A Java framework for multi-objective optimization, Advances in Engineering Software, Volume 42, Issue 10, 760-771, 2011,
実行コード
参考に上記の最適化を実行するコードを記載します。
import numpy as np
import optuna
import optuna.storages.journal
import optunahub
def objective(trial: optuna.Trial) -> tuple[float, float]:
# ZDT1
n_variables = 30
x = np.array([trial.suggest_float(f"x{i}", 0, 1) for i in range(n_variables)])
g = 1 + 9 * np.sum(x[1:]) / (n_variables - 1)
f1 = x[0]
f2 = g * (1 - (f1 / g) ** 0.5)
return f1, f2
def tpe_gamma(x: int) -> int:
return min(int(np.ceil(0.1 * x)), 50)
mod_sampler = optunahub.load_module("samplers/moead")
seed = 42
population_size = 100
n_trials = 10000
crossover = optuna.samplers.nsgaii.BLXAlphaCrossover()
samplers = [
optuna.samplers.RandomSampler(seed=seed),
optuna.samplers.NSGAIISampler(
seed=seed,
population_size=population_size,
crossover=crossover,
),
optuna.samplers.NSGAIIISampler(
seed=seed,
population_size=population_size,
crossover=crossover,
),
mod_sampler.MOEADSampler(
seed=seed,
population_size=population_size,
n_neighbors=population_size // 5,
scalar_aggregation_func="tchebycheff",
crossover=crossover,
),
optuna.samplers.TPESampler(
seed=seed,
n_startup_trials=500,
n_ei_candidates=50,
multivariate=True,
gamma=tpe_gamma,
),
]
studies = []
for sampler in samplers:
study_name = f"{sampler.__class__.__name__}"
study = optuna.create_study(
sampler=sampler,
study_name=study_name,
directions=["minimize", "minimize"]
)
study.optimize(objective, n_trials=n_trials)
studies.append(study)
optuna.visualization.plot_pareto_front(study).show()
mod_pfm = optunahub.load_module("visualization/plot_pareto_front_multi")
fig = mod_pfm.plot_pareto_front(studies)
fig.show()
reference_point = [1.0, 7.5]
mod_vhm = optunahub.load_module("visualization/plot_hypervolume_history_multi")
fig = mod_vhm.plot_hypervolume_history(studies, reference_point)
fig.show()
依存関係は以下で解決してください
pip install optuna optunahub scipy plotly