はじめに
本記事では数値流体解析によるパラメータ最適化を行います(前編:数値流体解析の準備)。
流体解析とは
弊社Tech blogでは主に構造解析に関する記事を取り扱ってきましたが、工学分野において構造解析と同じく重要視されているシミュレーションとして流体解析があります。現在流体が影響する製品(自動車、家電、船舶、飛行機、工場、etc...)であれば規模の多寡はあれど全く実施していない分野は無いと言っても過言ではないでしょう。
\frac{\partial \bold{u}}{\partial t} +(\bold{u} \cdot \nabla)\bold{u}= -\frac{1}{\rho} \nabla p + \nu (\nabla \cdot \bold{u}) +\bold{F}
m \bold{a} = \bold{F}に相当する上記流体運動の支配方程式であるNavie-Stokes方程式を解くことで流れ場を得ます(格子ボルツマン法等、他の手段もありますが今回は割愛)。
方程式そのものの発見は19世紀ですが、未だ解析解が発見されていない難しい式であり、大がかりな工業的適用は数値解を取得する手段である計算機の発展と共に歩んできました。
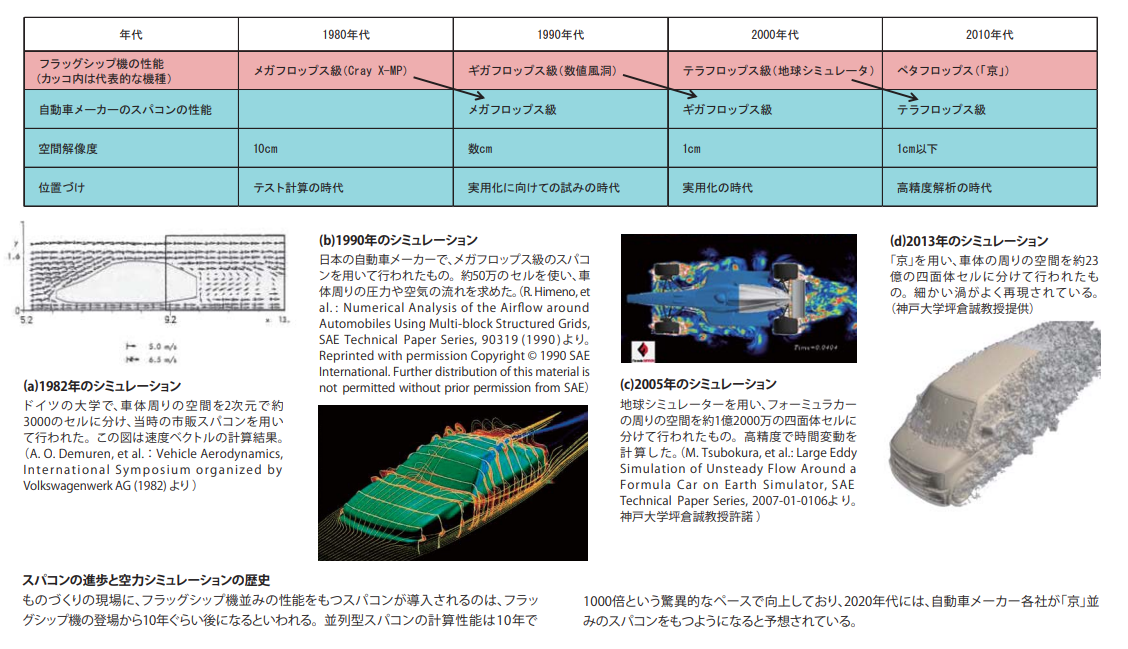 (理化学研究所 様から抜粋)
(理化学研究所 様から抜粋)
そんな前置きはさておき、実際に使ってみます。
OpenFOAM
最適化の前段階として、通常の流体解析を実施します。次の課題を設定します。
Φ=20 mm、L= 200 mm の一定速度で空気が一方向に流れる直管がある。この中間に回転方向の流れが生じる構造物(以下ミキサーと呼称)を設けることでなるべく圧損を上げずに旋回流を作り出す。
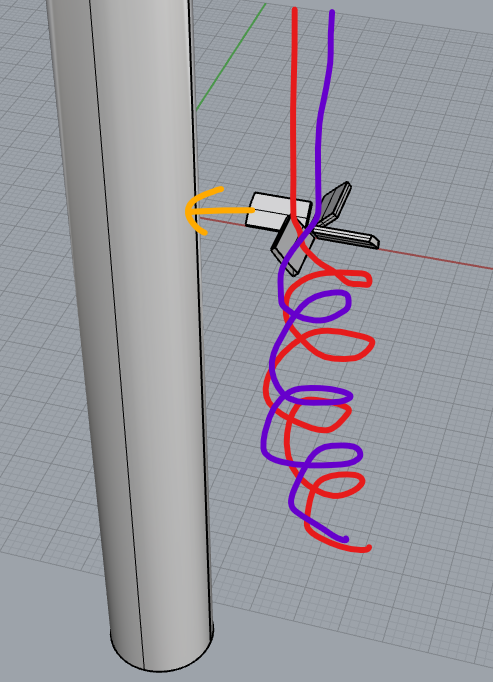
ある種の攪拌を想定した系になります。
OpenFOAMはおそらく最も有名なオープンソースの数値流体力学(連続体力学)ソフトウェアです。困った時の対応策も日文英文共にネットに多く転がっているので、無難な選択ではないでしょうか。(特にPENGUINITISさんとXSimさんにはお世話になっています。)
設定ファイルをバリバリ書けばそれに従ってモリモリ解析してくれます…が今回は内なるコンセプトとして比較的気軽に実行できる話にしたいと考えてますので、各種サンプルファイルをベースにして解析実行できるモノを組んでいきます。(前述のXSimさんはWeb上で設定ファイルを作成できるサービスを行っています、初心者にはそちらもおすすめです。)
なお、以降のメッシュ表示等には特記ない限り同じくオープンソースの可視化ソフトParaViewを使用しております。
解析準備
非圧縮定常の解析を行いたいのでベースとなる[インストールフォルダ]/tutorials/incompressible/simpleFoam/motorBike フォルダを作業箇所にコピーします。まずは形状をconstant/triSurfaceに用意しましょう。今回はstlで用意しました。
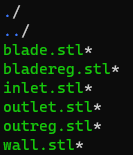 明確化の為、かつ後々の最適化時にファイル差し換えが簡単にできるように各形状(流入口、流出口、円筒管壁面、ミキサー形状)を別のファイルにしています。-regはメッシュの細分化(blade周辺、outlet直前5mm)領域を明示的に定義しています。
明確化の為、かつ後々の最適化時にファイル差し換えが簡単にできるように各形状(流入口、流出口、円筒管壁面、ミキサー形状)を別のファイルにしています。-regはメッシュの細分化(blade周辺、outlet直前5mm)領域を明示的に定義しています。
OpenFOAMは基本的にSI単位系で解析を実行しますが、メッシュ作成に使用するsnappyHexMeshが普通に使うと(m単位時の)mm以下の扱いがあまり得意でないので、本形状ぐらいのサイズの時は1000倍(=mm単位)で出力したstlでメッシュを作成し、後々0.001倍スケーリングした方が安定します。

こちらは試しに20×20(×10)mmのロゴに対して
・左...m単位でstlを出力して厚さ0.0001の壁面レイヤー挿入命令
・右...mm単位でstlを出力して厚さ0.1の壁面レイヤー挿入命令、メッシュ作成後全体を0.001倍
を実行した結果です。常に失敗する訳ではありませんが、最適化実行時は生成されたメッシュを一つ一つ確認することは現実的ではないので、なるべく安定的にメッシュを作成できる方法が良いです。
Allrunが実行スクリプトです。この記述を参考に各設定ファイル(systemフォルダ内に実行名と同名ファイルが存在しています)を調整していきましょう。以下、設定を行う時に私が気を付けていることを書き出してみました。
・decomposeParDict...並列化設定です。今回のように一方向に長い形状の時はその方向のみ分割する設定にします。
・surfaceFeatureExtract...形状の特徴線を抽出してメッシュ作成時の参考にします。ミキサーのように明らかに形状の再現度が最終的な結果に大きく影響する形状に実施します。
・blockMeshDict、snappyHexMesh...メッシュ作成に関連しています。あまり他のメッシャーでは見られない方法でメッシュを作成していますので、他流体解析を実施されたことのある方も各種解説を一度確認してから使用した方がいいでしょう。
今回は最適化後のミキサーでも十分解析の精度を担保できるようにミキサーがとる範囲全体を集中的に細分化しています。また、出口近傍も運動量を取得する為に細分化を施しています。

・potentialFoam...ポテンシャル流れ(粘性のない流れ、簡単に解ける)を解いて初期値として場に与えます。解析初期の値の急激な変化を防ぐことができ、最終的な値の収束が早くなったり発散を防ぐ効果が見込まれますが、一方で与えらえた初期値に最終的な解が悪影響を受けて不正確な値を導くこともあります。ケースバイケースで適用可否を検討します。今回は使用しています。
・$(getApplication)...system/controlDictのapplicationにあるソルバ(simpleFoam)を実行します。収束計算の実行回数等もcontrolDictで設定します。適宜値を設定してください。また、ポスト処理用にfunctionsで出口近傍領域の角運動量を出力するようにします。[インストールフォルダ]/tutorials/incompressible/simpleFoam/pipeCyclicの記述が参考になります。残差も後々収束確認を行う為に出力しておきます。functions内に以下の行を記述します。
#includeFunc solverInfo
追加で以下の実行設定をします。
・transformPoints -scale "(1e-3 1e-3 1e-3)"...toposetの後に実行します。mmで作成されているメッシュをm単位にリスケール(×0.001)します。
・postProcess -func 'patchAverage(name=inlet, p)'
...最終行に記述します。inletの圧力を出力します。
以上を書き足して実行します。出力されたlogにエラーがなければひとまず成功です。ダメだった場合は適宜修正の後にリトライしましょう。Allcleanでリフレッシュします(こちらも初期状態だとtriSurface内の形状データも消してしまうので適宜書き換えてください)。
最適化に向けた確認事項
パラメータ最適化で使用することを念頭に、以下の検討、調整を行います。
・solverInfoに出力されている各種残差をプロットして、収束しているか確認します。パラメータ最適化を行う際に生成される形状次第では収束しにくい流れが生じる可能性があることから、若干余裕をもって多めのiteration数にしておきます。今回の場合、1500~2000回程度がよさそうです。
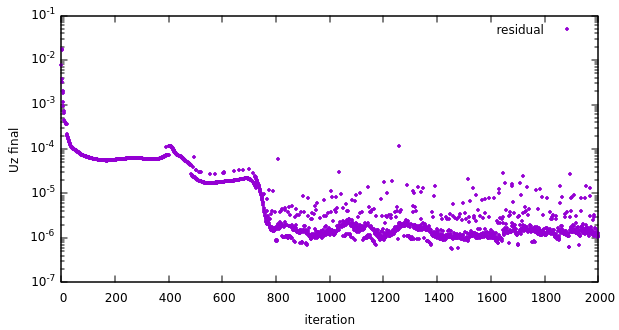 緩和係数の調整や収束判定条件を設けて計算を適宜打ち切る、逆にギリギリの回数を攻めて一回の解析にかかる計算時間を減らし、計算実行の総回数を増やした方がいいのではないか?等ここは色々な流派があるので、自分の肌感覚と計算対象に合う方向性を選ぶといいのではないでしょうか。
緩和係数の調整や収束判定条件を設けて計算を適宜打ち切る、逆にギリギリの回数を攻めて一回の解析にかかる計算時間を減らし、計算実行の総回数を増やした方がいいのではないか?等ここは色々な流派があるので、自分の肌感覚と計算対象に合う方向性を選ぶといいのではないでしょうか。
・一回の解析にかかる計算時間を計測しておきます。最適化を実施する際の総時間のおおよその目安となります。
・何個か実際にミキサー形状のstlを差し換えて計算し、問題なく計算が実行されるか確認します。
・結果を可視化し、明らかに異常な流れが生じていないか調べます。例えば出口から逆流していないか、非連続的な値が生じていないか等です。
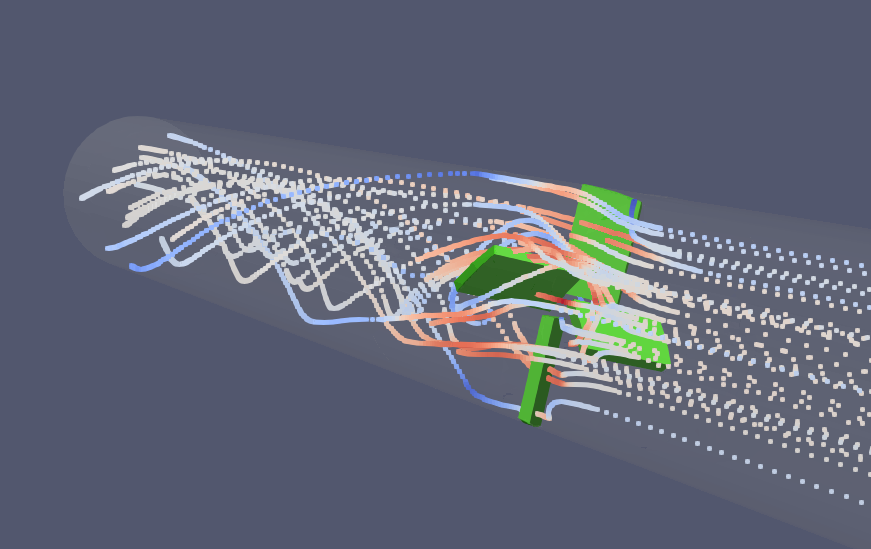 流線を表示しています。紙面右側から円筒軸方向垂直に流れていた流れが緑色のミキサーにあたって旋回流になっていることが分かります。
流線を表示しています。紙面右側から円筒軸方向垂直に流れていた流れが緑色のミキサーにあたって旋回流になっていることが分かります。
まとめ
流体解析を用いたパラメータ最適化実施の前段階として、OpenFOAMの設定をし、実際に解析してみました。後編でパラメータ最適化します。



 (
(
 明確化の為、かつ後々の最適化時にファイル差し換えが簡単にできるように各形状(流入口、流出口、円筒管壁面、ミキサー形状)を別のファイルにしています。-regはメッシュの細分化(blade周辺、outlet直前5mm)領域を明示的に定義しています。
明確化の為、かつ後々の最適化時にファイル差し換えが簡単にできるように各形状(流入口、流出口、円筒管壁面、ミキサー形状)を別のファイルにしています。-regはメッシュの細分化(blade周辺、outlet直前5mm)領域を明示的に定義しています。

 緩和係数の調整や収束判定条件を設けて計算を適宜打ち切る、逆にギリギリの回数を攻めて一回の解析にかかる計算時間を減らし、計算実行の総回数を増やした方がいいのではないか?等ここは色々な流派があるので、自分の肌感覚と計算対象に合う方向性を選ぶといいのではないでしょうか。
緩和係数の調整や収束判定条件を設けて計算を適宜打ち切る、逆にギリギリの回数を攻めて一回の解析にかかる計算時間を減らし、計算実行の総回数を増やした方がいいのではないか?等ここは色々な流派があるので、自分の肌感覚と計算対象に合う方向性を選ぶといいのではないでしょうか。

