リンク機構を「解く」：連続最適化による機構設計入門

はじめに

NatureArchitects社では最適化と物理シミュレーションを組み合わせた設計手法を日々模索しており、時折こんな問いが生まれる。「好きな軌跡を描くリンク機構を、自動的に設計できないだろうか？」

確かに、一般的なパラメトリックCADシステムは、ユーザーが設計パラメータを直接指定し、その動きをシミュレートする（順問題）ことに特化しているが、所望の軌跡からパラメータを逆算する（逆問題）機能は限定的である。近年の研究では逆設計の試み[1]もあるが、汎用的・インタラクティブな逆問題ソルバーはまだ未成熟と言える。

この問いに答えるには、まず順問題として「機構の動きのシミュレーションをどう解いているか」を連続最適化の文脈で理解するとよいだろう。連続最適化による解法は、逆問題を解く上での良い共通基盤となる。この枠組みは、コンピュータ、CAD、GUIの歴史や哲学、そしてNatureArchitects社の折り紙ソルバーCrane[2]とも深く結びついているからだ。(図1)

図1: NatureArchitects社による折り紙ソルバー Crane で作成したオブジェクト。折り紙の性質を活用して、平面から家具のような大きな構造物も設計・製造することができる。

本記事では60年前のSketchpadの数理を連続最適化の形で紹介しブラウザ上に再現することで、その哲学を追体験していく。この記事の内容が腑に落ちる頃には、自分でリンク機構のシミュレータを実装できるようになるだろう。

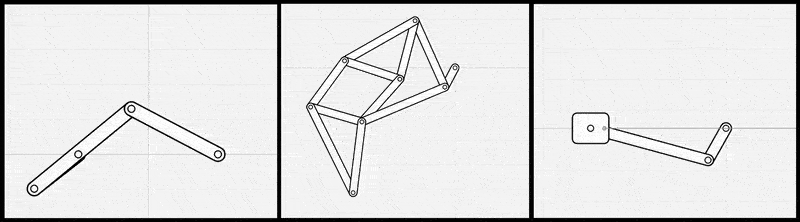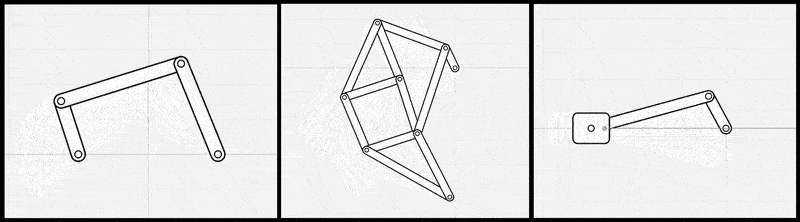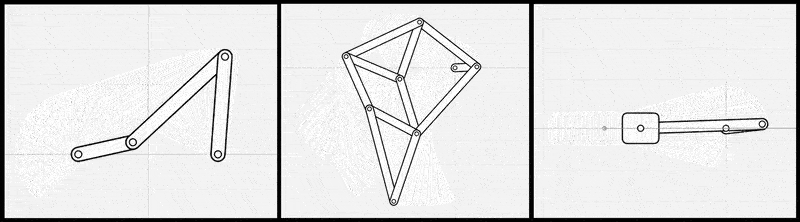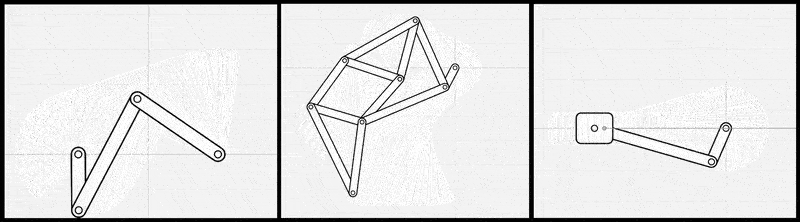
図2: リンク機構シミュレータを線形代数ライブラリとp5.jsで自前で実装した例

Sketchpadから機構設計へ

Ivan Sutherland は1963年の博士論文 "Sketchpad: A Man-Machine Graphical Communication System" で、新しいコンピュータ支援設計手法を提示した [3]。Sutherland のビジョンは、コンピュータを単なる計算機でも描画ツールとして使うことだけではなかった。それまで図面として成立するための幾何学的な制約要件を設計者が手で解いていた問題を、コンピュータに自動で解かせ、設計者がよりクリエイティブな仕事に集中できるような仕組みにあった。

図3: Ivan Sutherland による Sketchpadの装置（TX-2）とライトペン

そのビジョンを具現化したコンセプトとしてSutherlandが開発したSketchpad では、設計者がライトペンと呼ばれる特殊なデバイスで画面上に図形を描き、図形間の幾何学的関係を制約条件として指定できる（図3）。2点間の距離が一定、2本の線が平行といった関係を指定すると、システムは制約を満たすように図形を自動的に調整する。この振る舞いは、制約違反を最小化する最適化問題として数学的に定式化される：

\min_{\mathbf{x}} \quad f(\mathbf{x}) = \frac{1}{2} \|\mathbf{r}(\mathbf{x})\|^2

\mathbf{x} を設計変数（点の座標など）、\mathbf{r}(\mathbf{x}) = (r_1(\mathbf{x}), \ldots, r_m(\mathbf{x}))^T を幾何学的制約の残差ベクトル（residual vector）とする。

Sketchpad の応用例の中でも、Sutherland 自身が注目したのが、リンク機構の設計であった。論文第9章 "Recursive Operations" (pp. 94-96) でこう述べている：

By far the most interesting application of Sketchpad so far has been drawing and moving linkages.

（訳）これまでのところ、Sketchpadの最も興味深い応用は、リンク機構を描いて動かすことである。

論文で紹介された別の例としては3つの動く部品からなるリンク機構が、多様な軌跡を生成する様子が示されている。Sutherland は以下のように記している：

The driving link was rotated by turning a knob below the scope. Total time to construct the linkage was five minutes, but over an hour was spent playing with it.

（訳）駆動リンクはスコープの下にあるノブを回すことで回転させた。リンク機構を構築する総時間は5分であったが、それで遊ぶのに1時間以上費やした。

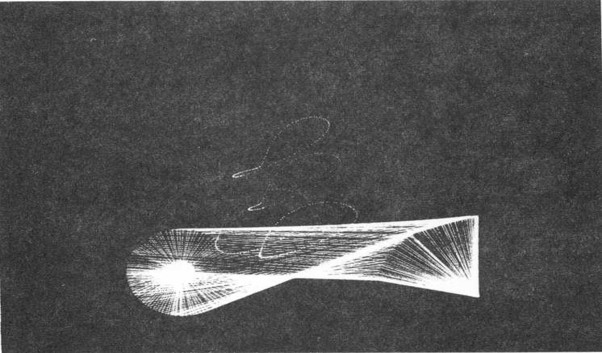
図4: Ivan Sutherland が1時間遊ぶのに費やしたリンク機構の写真

つまり、GUIもマウスも実用化される前の1963年の時点で、連続最適化による制約充足と人間とのインタラクティブな調整を組み合わせるという設計哲学がすでに存在していたのである。この思想が現代のCADシステムの基礎となり、60年以上が経過した現在、静的な幾何形状の制約ベース設計は成熟した技術となっている。

それでは、制約充足問題を解くためには何をすればよいのだろうか？本章では、最小二乗問題に特化した解法であるガウス・ニュートン法を始めとした各種手法を紹介しながら、リンク機構がなぜこの手法で順問題として解けるのかを理解していこう。

連続最適化入門

本章では勾配、ヤコビ行列、ヘッセ行列といった多変数微積分の概念を使用する。もし独学で学ぶには Multivariable Calculus と検索したり、体系的な学習を望む読者には、Nocedal & Wright "Numerical Optimization" (Springer, 2006)[4] や金森ら『機械学習のための連続最適化』(講談社, 2016)[5] を参照されたい。

目的関数

連続最適化問題を数値的に解くには、目的関数（objective function）の微分情報が必要となる。最適化問題の基本形は以下のように表される：

\min_{\mathbf{q}} \quad f(\mathbf{q})

ここで、最適化変数と目的関数を以下のように定義する：

\mathbf{q} \in \mathbb{R}^n, \quad f: \mathbb{R}^n \to \mathbb{R}

\mathbb{R} は実数全体の集合、\mathbb{R}^n は n 次元実数ベクトル空間を表す。また f: \mathbb{R}^n \to \mathbb{R} は、f が n 次元ベクトルを入力として実数スカラーを出力する関数であることを示す。

勾配

n 次元ベクトル \mathbf{q} \in \mathbb{R}^n を変数とするスカラー関数 f: \mathbb{R}^n \to \mathbb{R} の勾配（gradient）は、各変数に関する偏微分を並べたベクトルであり、\nabla f(\mathbf{q}) で表される：

\nabla f(\mathbf{q}) = \begin{bmatrix} \frac{\partial f}{\partial q_1} \\ \frac{\partial f}{\partial q_2} \\ \vdots \\ \frac{\partial f}{\partial q_n} \end{bmatrix} \in \mathbb{R}^n

記号 \nabla をナブラと呼び、微分作用素を表す。デルタではない。勾配ベクトルは関数が最も急激に増加する方向を指し、最適化において探索方向を決定する基本的な情報となる。

ヘッセ行列

勾配をさらに微分するとヘッセ行列（Hessian matrix）が得られる。これは2階偏微分を並べた対称行列であり、関数の曲率を表す。ヘッセ行列は H(f) で表記されるが、\nabla^2 f(\mathbf{q}) という表記も用いられることがある。本記事では H(f) を用いる：

H(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial q_1^2} & \cdots & \frac{\partial^2 f}{\partial q_1 \partial q_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial q_n \partial q_1} & \cdots & \frac{\partial^2 f}{\partial q_n^2} \end{bmatrix}

名称はドイツの数学者 Ludwig Otto Hesse（1811–1874）に由来する。Hesseは1857年の論文[6]で2階偏微分の行列式（die Determinante der zweiten Differentiale）について論じたが、後世でヘッセ行列（Hessian matrix）と名付けられた。

なお、物理学や偏微分方程式の文脈では \nabla^2 f はラプラシアン（Laplacian）と呼ばれるスカラー演算子を指すことが多い。ラプラシアンは勾配の発散として定義され、ユークリッド座標系におけるスカラー関数に対して、ヘッセ行列の対角成分の和、すなわちトレースに相当する：

\Delta f = \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \cdots

ラプラシアンは \Delta でも表記され、この記号はデルタと読む。名称はフランスの数学者 Pierre-Simon Laplace（1749–1827）に由来する。このように \nabla^2 f という記号はラプラシアンとの混同を避けるため、本記事ではヘッセ行列には H(f) を用いる。

ヤコビ行列

またさらにややこしいのが、ベクトル値関数の微分はヤコビ行列（Jacobian matrix）もしくはヤコビアンと呼ばれるものである。スカラー関数 f: \mathbb{R}^n \to \mathbb{R} に対してヘッセ行列が2階微分を表すのに対し、ベクトル値関数 \mathbf{g}: \mathbb{R}^n \to \mathbb{R}^m に対してヤコビ行列は1階微分を表す：

\mathbf{J}(\mathbf{q}) = \frac{\partial \mathbf{g}}{\partial \mathbf{q}} \in \mathbb{R}^{m \times n}

[\mathbf{J}]_{ij} = \frac{\partial g_i}{\partial q_j}

\mathbf{J}(\mathbf{q}) = \begin{bmatrix} \frac{\partial g_1}{\partial q_1} & \cdots & \frac{\partial g_1}{\partial q_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial g_m}{\partial q_1} & \cdots & \frac{\partial g_m}{\partial q_n} \end{bmatrix} = \begin{bmatrix} \nabla g_1(\mathbf{q})^T \\ \nabla g_2(\mathbf{q})^T \\ \vdots \\ \nabla g_m(\mathbf{q})^T \end{bmatrix}

ヤコビ行列は \mathbf{g} の各成分それぞれの勾配を縦に並べたものと理解するとわかりやすい。この名称はドイツの数学者 Carl Gustav Jacob Jacobi（1804–1851）に由来する。Jacobiは1841年の論文[7]で関数的行列式（Determinans functionalis）について論じたが、後世でベクトル値関数の微分としてヤコビ行列（Jacobian matrix）と名付けられた。

ヤコビ行列は一般的な微分の概念であり、ヘッセ行列はその特殊ケースとして理解できる。スカラー関数 f: \mathbb{R}^n \to \mathbb{R} の勾配 \nabla f: \mathbb{R}^n \to \mathbb{R}^n はベクトル値関数であり、この勾配ベクトルに対するヤコビ行列が、ヘッセ行列そのものである：

H(f) = \frac{\partial (\nabla f)}{\partial \mathbf{q}} = \mathbf{J}_{\nabla f}(\mathbf{q})

最急降下法

最小化問題を解く最も基本的な方法は目的関数の勾配を活用した最急降下法（steepest descent method, gradient descent）である。目的関数の勾配の逆方向に一定のステップで進む手法であり、以下のように表される：

\mathbf{q}_{k+1} = \mathbf{q}_k - \alpha \nabla f(\mathbf{q}_k)

\alpha > 0 はステップサイズであり、機械学習の分野では学習率とも呼ばれる。

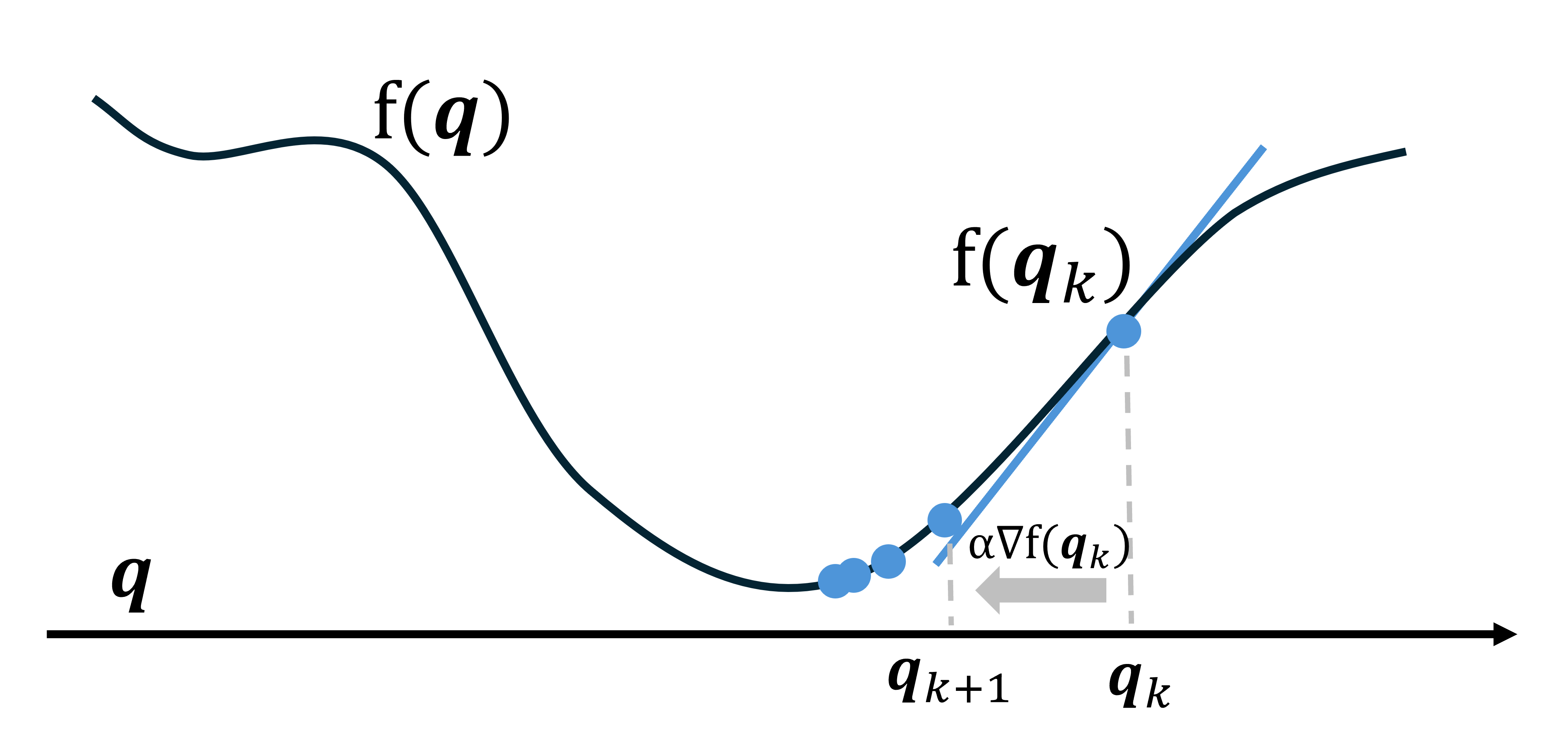
図5: 最急降下法は負の勾配を利用することで最適解に向かう

最急降下法は実装が簡単で広く知られているが、最適解に到達するにつれ移動距離も縮んでしまう影響や、歪んだ谷をみたときに非効率的な方向を示してしまう影響もあって、反復回数が比較的膨大に必要になることがある。

ニュートン法

最小化問題において、勾配だけでなく2階微分を活用した手法「ニュートン法」を紹介する。ニュートン法は(局所的には)二次収束呼ばれる特徴により、最急降下法よりも最適解近傍で劇的に高速に収束し、反復回数が指数的に減少するメリットがある。更新式は以下の通りである：

\mathbf{q}_{k+1} = \mathbf{q}_k - H(f(\mathbf{q}_k))^{-1} \nabla f(\mathbf{q}_k)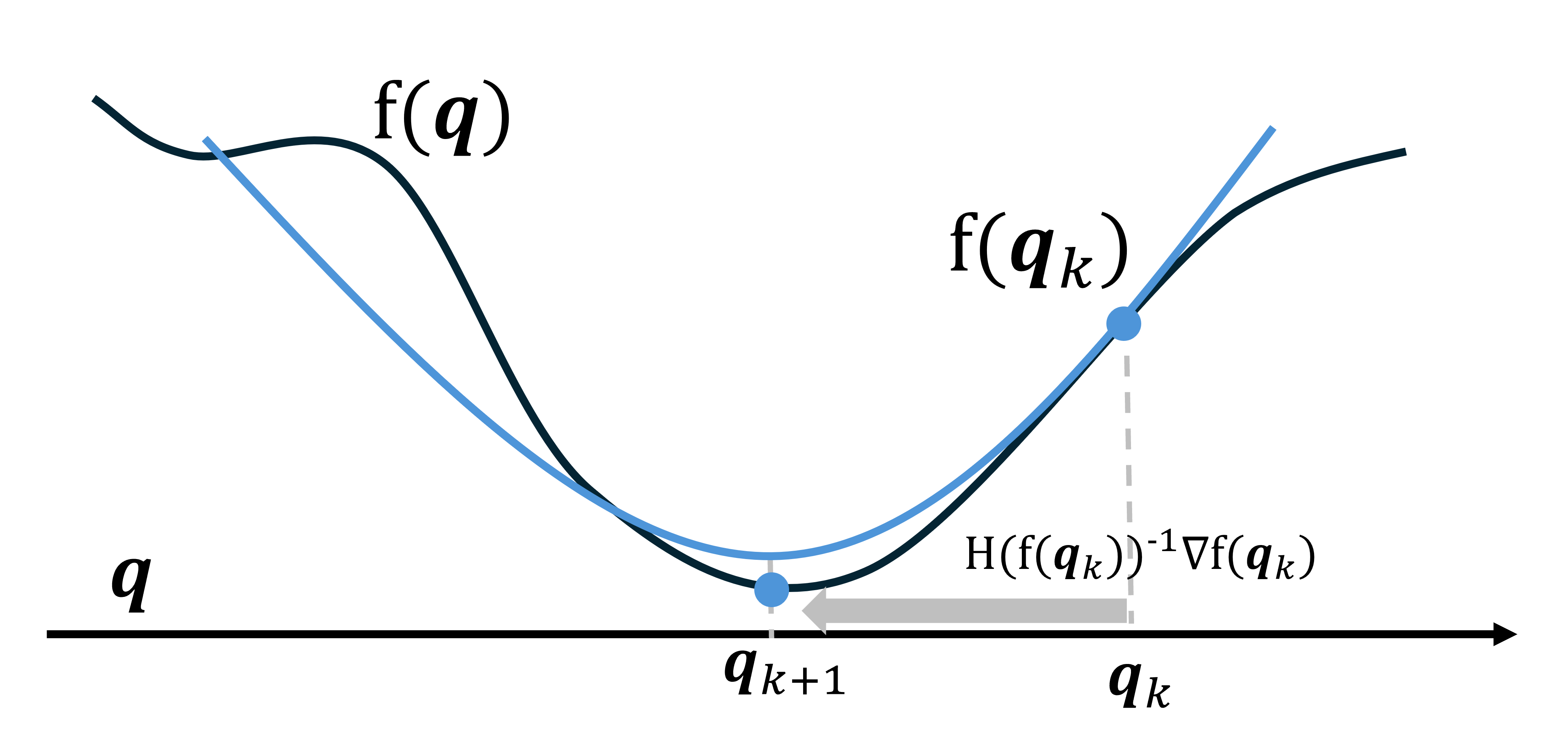

図6: ニュートン法は２階微分を活用し探索する。

ニュートン法による最小化の発想としては、極値においては勾配 \nabla f(\mathbf{q}) = \mathbf{0} 、つまり最適性条件を満たす解を導き出すことである。具体的には \nabla f(\mathbf{q})をテイラー展開すると

\nabla f(\mathbf{q}_k + \Delta\mathbf{q}) \approx \nabla f(\mathbf{q}_k) + H(f(\mathbf{q}_k)) \Delta\mathbf{q}

二次以降を無視して近似した場合に=0になる場所を導出すると以下のような式が導き出せる。

\nabla f(\mathbf{q}_k) + H(f(\mathbf{q}_k)) \Delta\mathbf{q} = \mathbf{0}

これを \Delta\mathbf{q} について整理すると

\Delta\mathbf{q} = -H(f(\mathbf{q}_k))^{-1} \nabla f(\mathbf{q}_k)

この更新量を用いて \mathbf{q}_{k+1} = \mathbf{q}_k + \Delta\mathbf{q} とすることで、冒頭で示したニュートン法の更新式が得られる。

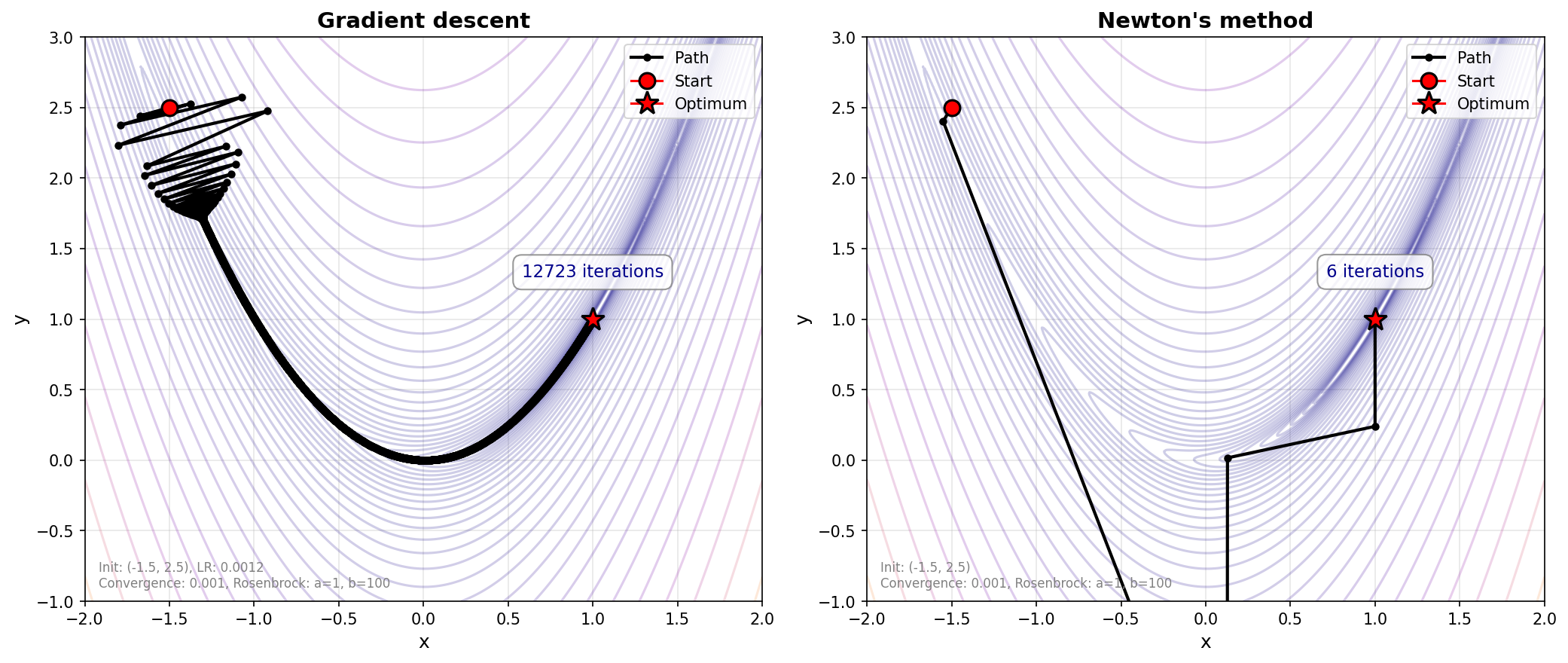
図7: 最急降下法（左）とニュートン法（右）のRosenbrock関数を目的関数としたときの収束の仕方の比較。最急降下法よりもニュートン法が少ないイテレーションで解にたどり着いている様子がわかる。

もしかしたらニュートン法と聞くと、方程式 h(x) = 0 の根を求める手法を思う人がいるかもしれない。ニュートンとラフソンが独立に考案した手法は以下の通りである：

x_{k+1} = x_k - \frac{h(x_k)}{h'(x_k)}

17世紀のニュートンとラフソンが考案した手法は1変数の根を求める方法であり、多変数最適化への拡張やヘッセ行列を用いた手法は後世の数学者による発展となる。基本的な原理は同じなので、両者とも「ニュートン法」あるいは「ニュートン・ラフソン法」と呼ばれる。

\mathbf{q}_{k+1} = \mathbf{q}_k - \frac{\nabla f(\mathbf{q}_k)}{(\nabla f)'(\mathbf{q}_k)} = \mathbf{q}_k - H(f(\mathbf{q}_k))^{-1} \nabla f(\mathbf{q}_k)

今後ニュートン法と呼ぶ際には、基本的に連続最適化の文脈におけるニュートン法を示すこととする。しかしながら、この名称が混乱を招く問題が、連続最適化初学者の地味な障壁になっているのではないか、という指摘をいただくことがある。

正定値性

ニュートン法を紹介した際、目的関数の勾配 \nabla f(\mathbf{q}) = \mathbf{0} に誘導する行為に違和感を覚えた方は鋭い。極値であるからといって、それが極小値であることは保証されない。極大値や鞍点の可能性もあるからだ。

まず1変数関数 f(x) で考えてみよう。極値 f'(x) = 0 が極小値であるかを判定するには、2階微分 f''(x) を用いる。2階微分が正 f''(x) > 0 であれば、その点が極小値であることが判定できる：

f'(x) = 0 \quad \text{and} \quad f''(x) > 0 \quad \Rightarrow \quad x \text{ is a local minimum}

それでは多変数関数における2階微分、すなわちヘッセ行列 H(f) が「正」であるかをどのように判定すればよいのだろうか。ここで登場するのが正定値性（positive definiteness）という概念である。

対称行列 \mathbf{A} \in \mathbb{R}^{n \times n} が正定値であるとは、以下の3つの同値な条件のいずれかが成り立つことである。

1. 二次形式による定義 — 任意の非零ベクトル \mathbf{x} \neq \mathbf{0} に対して

\mathbf{x}^T \mathbf{A} \mathbf{x} > 0

2. 固有値による判定 — \mathbf{A} のすべての固有値 \lambda_i が正（\lambda_i > 0）

3. コレスキー分解可能性 — 上三角行列 \mathbf{L} を用いて \mathbf{A} = \mathbf{L}^T \mathbf{L} と分解できる

幾何学的には、2次関数 f(\mathbf{x}) = \frac{1}{2}\mathbf{x}^T \mathbf{A} \mathbf{x} がお椀型であること、すなわち唯一の最小点を持つことを意味する。

コレスキー分解（Cholesky decomposition）

実対称行列（または複素エルミート行列） \mathbf{A} が正定値であることと、上三角行列 \mathbf{L} を用いて \mathbf{A} = \mathbf{L}^T \mathbf{L} と分解できることは同値である。以下のように示される：

\mathbf{x}^T \mathbf{A} \mathbf{x} = \mathbf{x}^T (\mathbf{L}^T \mathbf{L}) \mathbf{x} = (\mathbf{L}\mathbf{x})^T (\mathbf{L}\mathbf{x}) = \|\mathbf{L}\mathbf{x}\|^2 > 0

\mathbf{L} が正則ならば任意の非零ベクトル \mathbf{x} \neq \mathbf{0} に対して \mathbf{L}\mathbf{x} \neq \mathbf{0} となり、\|\mathbf{L}\mathbf{x}\|^2 は必ず正である。逆も成り立ち、正定値性とコレスキー分解可能性は同値になる。

フランスの数学者André-Louis Choleskyが第一次世界大戦における測地学の計算のために開発したこの手法は、数値的に安定でLU分解の約2倍高速である。

さらに実務上の利点として、正定値性を判定する際、コレスキー分解は固有値分解よりも計算効率が高い。固有値分解が O(n^3) の演算量を要するのに対し、コレスキー分解は O(n^3/3) で済む。このため、数値最適化ライブラリでは、行列が正定値かどうかを確認する手段としてコレスキー分解の成否を利用することが一般的である。

修正ニュートン法

ヘッセ行列が正定値でない場合、つまり鞍点、特異性、非凸領域のような状況では、ニュートン法は収束できず失敗する。それを解決したのが、ダンピング項（正則化項）\epsilon \mathbf{I} を加えてヘッセ行列を強制的に正定値にする修正ニュートン法である。

(H(f(\mathbf{q})) + \epsilon \mathbf{I}) \Delta\mathbf{q} = -\nabla f(\mathbf{q})

ここで重要な性質は、任意の行列 \mathbf{A} に対して \mathbf{A} + \epsilon \mathbf{I} の固有値は \mathbf{A} の固有値に \epsilon を加えたものになることである。これは固有値の定義 \mathbf{A}\mathbf{v} = \lambda \mathbf{v} から直接導かれる：

(\mathbf{A} + \epsilon \mathbf{I})\mathbf{v} = \mathbf{A}\mathbf{v} + \epsilon \mathbf{v} = \lambda \mathbf{v} + \epsilon \mathbf{v} = (\lambda + \epsilon)\mathbf{v}

したがって、\epsilon \mathbf{I} を加えると全ての固有値が \lambda_i \to \lambda_i + \epsilon とシフトする。

\epsilon が小さいほどニュートン法に近く高速、大きいほど最急降下法に近く安定となる。この正則化の考え方は、次節のレーベンバーグ・マルカート法（Levenberg–Marquardt method）の基礎となっている。

最小二乗問題とニュートン法

拘束充足問題を解くには、拘束違反を測定する目的関数を定義し、それを最小化する問題に帰着できる。残差ベクトルのノルム二乗を用いて以下のように定式化する：

\mathbf{r}(\mathbf{q}) \in \mathbb{R}^m

f(\mathbf{q}) = \frac{1}{2}\|\mathbf{r}(\mathbf{q})\|^2 = \frac{1}{2}\mathbf{r}(\mathbf{q})^T\mathbf{r}(\mathbf{q})

全ての拘束が満たされる場合、\mathbf{r}(\mathbf{q}) = \mathbf{0} であり f(\mathbf{q}) = 0 となる。拘束充足問題は以下の最小化問題として定式化される：

\min_{\mathbf{q}} \quad f(\mathbf{q}) = \frac{1}{2}\|\mathbf{r}(\mathbf{q})\|^2

これが、最小二乗問題（least squares problem）と呼ばれる形式である。

ガウス・ニュートン法

最小二乗問題 f(\mathbf{q}) = \frac{1}{2}\|\mathbf{r}(\mathbf{q})\|^2 に対するニュートン法を考える。\mathbf{J}(\mathbf{q}) = \frac{\partial \mathbf{r}}{\partial \mathbf{q}} \in \mathbb{R}^{m \times n} を残差ベクトルのヤコビ行列とすると、勾配とヘッセ行列は以下のように表される：

\nabla f(\mathbf{q}) = \mathbf{J}(\mathbf{q})^T \mathbf{r}(\mathbf{q})

H(f(\mathbf{q})) = \mathbf{J}(\mathbf{q})^T \mathbf{J}(\mathbf{q}) + \mathbf{r}(\mathbf{q})^T \cdot \mathbf{H}(\mathbf{r}(\mathbf{q}))

ここで、目的関数のヘッセ行列の第二項は各残差関数の2階微分を計算して合計する必要がある。

この残差ベクトルの二階微分の計算は、実務においてかなり扱いづらいらしい。というのも、行列ですらなく三階テンソルになってしまうからだ。実際のところ、最適解近傍では \mathbf{r}(\mathbf{q}) \approx \mathbf{0} となるため、この項の影響は計算が大変な割に大きくない。

そんな理由もあって、残差ベクトルの二階微分、すなわち三階のテンソル計算が必要な第二項を無視すると、最小二乗問題に特化したニュートン法の近似版であるガウス・ニュートン法が得られる：

H(f(\mathbf{q})) \approx \mathbf{J}(\mathbf{q})^T \mathbf{J}(\mathbf{q})

\mathbf{q}_{k+1} = \mathbf{q}_k - (\mathbf{J}_k^T \mathbf{J}_k)^{-1} \mathbf{J}_k^T \mathbf{r}_k

ここで \mathbf{J}_k = \mathbf{J}(\mathbf{q}_k), \mathbf{r}_k = \mathbf{r}(\mathbf{q}_k) である。

この手法が「ガウス・ニュートン法」と呼ばれるのは、Carl Friedrich Gauss が1809年の著作『Theoria motus corporum coelestium』[8]において観測方程式の線形化と誤差の二乗和最小化の理論的基盤を確立したことに由来する。ただし、この反復アルゴリズムの形式自体は、19世紀後半にニュートン法と結合されて確立されたものであり、ガウス自身が明示的に提示したものではない。

また、(\mathbf{J}_k^T \mathbf{J}_k)^{-1} \mathbf{J}_k^T は、ヤコビ行列の擬似逆行列（Moore–Penrose pseudoinverse）とも呼ばれ、\mathbf{J}_k^+ と表記される。これを用いると以下のように書ける：

\mathbf{q}_{k+1} = \mathbf{q}_k - \mathbf{J}_k^+ \mathbf{r}_k

レーベンバーグ・マルカート法

ガウス・ニュートン法には、ニュートン法が本来持つ性質と近似の影響の両方によって数値的な問題があることが知られている。例えば、\mathbf{J}_k^T \mathbf{J}_k が特異に近い場合には、逆行列の計算が不安定となる。これを改善したものがレーベンバーグ・マルカート法[9][10]（Levenberg-Marquardt method）である。

レーベンバーグ・マルカート法は、修正ニュートン法と似たような正則化により、この問題を解決する。減衰項 \lambda \geq 0 を導入し、正規方程式を以下のように変更する：

(\mathbf{J}_k^T \mathbf{J}_k + \lambda \mathbf{I}) \Delta\mathbf{q}_k = -\mathbf{J}_k^T \mathbf{r}_k

\lambda を適応的に調整する信頼領域法（trust-region method）と呼ばれる手法で安定的に収束させる事ができる。Kenneth Levenbergが1944年に提案し、Donald Marquardtが1963年に改良した。

リンク機構の順問題定式化

前章で解説したガウス・ニュートン法を用いるには、問題を「残差ベクトル \mathbf{r}(\mathbf{q}) のノルム二乗を最小化する」形式で定式化する必要がある。本章では、リンク機構の拘束充足問題をこの形式で定式化する。

一般化座標として表す最適化変数

リンク機構は2つの基本要素で構成される。リンク (Link) は剛体部品であり、位置と姿勢を持つ最適化変数として扱う。ジョイント (Joint) は部品間の幾何学的拘束関係であり、固定パラメータとして扱う。

リンクの集合を \mathcal{L} = \{1, 2, \ldots, n\} とすると、各リンク i \in \mathcal{L} の状態は、位置ベクトル \mathbf{x}_i = [x_i, y_i]^T \in \mathbb{R}^2 と姿勢角 \varphi_i \in \mathbb{R} で表現される。機構全体の状態を記述する一般化座標ベクトル（generalized coordinates）\mathbf{q} を以下のように定義する：

\mathbf{q} = [\mathbf{x}_1^T, \varphi_1, \mathbf{x}_2^T, \varphi_2, \ldots, \mathbf{x}_n^T, \varphi_n]^T \in \mathbb{R}^{3n}

これが最適化問題で更新される変数である。なお、固定リンク、すなわちグラウンドリンク（ground link）の状態は既知定数として扱い、\mathbf{q} から除外する。

固定パラメータとしてのジョイント定義

ジョイント Joint は、リンク間の幾何学的制約を表現する。本稿では、最も基本的な回転ジョイント（revolute joint）を扱う。ピンジョイント（pin joint）とも呼ばれるこの制約は、2つのリンクが特定の点で接続され、その点を中心に相対的に回転できることを表す。

ジョイントの集合を \mathcal{J} = \{1, 2, \ldots, m\} とする。各ジョイント j \in \mathcal{J} は、接続するリンクのインデックスペア (i_j, k_j) \in \mathcal{L}^2 と、各リンクのローカル座標系における接続点で定義される：

j = (i_j, k_j, \mathbf{r}_{i_j}^{\text{local}}, \mathbf{r}_{k_j}^{\text{local}})

ここで以下が成り立つ：

(i_j, k_j) \in \mathcal{L}^2, \quad \mathbf{r}_{i_j}^{\text{local}}, \mathbf{r}_{k_j}^{\text{local}} \in \mathbb{R}^2

これらのパラメータは機構の設計で決まる固定値であり、最適化では変化しない。接続するリンクのペアと接続点のローカル座標がこれに含まれる。

座標変換と拘束関数

リンク i 上のローカル座標（local coordinates）\mathbf{r}_i^{\text{local}} をワールド座標（world coordinates）に変換する関数を以下のように定義する：

\mathbf{x}_i^{\text{world}}(\mathbf{r}_i^{\text{local}}) = \mathbf{x}_i + \mathbf{R}(\varphi_i) \mathbf{r}_i^{\text{local}}, \quad \mathbf{R}(\varphi) = \begin{bmatrix} \cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi \end{bmatrix}

ジョイント j = (i_j, k_j, \mathbf{r}_ {i_j}^{\text{local}}, \mathbf{r}_ {k_j}^{\text{local}}) \in \mathcal{J} に対する拘束関数を次のように定義する。これにより、接続された2つのリンク上の点のワールド座標における位置の差を表す。拘束が満たされる場合、すなわち2つの点が完全に一致する場合に \mathbf{r}_j(\mathbf{q}) = \mathbf{0} となる。

\mathbf{r}_j(\mathbf{q}) = \mathbf{x}_{i_j}^{\text{world}}(\mathbf{r}_{i_j}^{\text{local}}) - \mathbf{x}_{k_j}^{\text{world}}(\mathbf{r}_{k_j}^{\text{local}}) \in \mathbb{R}^2

残差ベクトルとヤコビ行列

|\mathcal{J}| をジョイントの総数とするとき、全てのジョイントの拘束関数を縦に積み重ねた全体の拘束ベクトル \mathbf{r} : \mathbb{R}^{3n} \to \mathbb{R}^{2|\mathcal{J}|} を以下のように定義する：

\mathbf{r}(\mathbf{q}) = \begin{bmatrix} \mathbf{r}_{j_1}(\mathbf{q}) \\ \mathbf{r}_{j_2}(\mathbf{q}) \\ \vdots \\ \mathbf{r}_{j_{|\mathcal{J}|}}(\mathbf{q}) \end{bmatrix} \in \mathbb{R}^{2|\mathcal{J}|}

拘束ベクトル \mathbf{r}(\mathbf{q}) が定義されると、順問題は第2章で解説した最小二乗問題として定式化される：

\min_{\mathbf{q}} \quad f(\mathbf{q}) = \frac{1}{2}\|\mathbf{r}(\mathbf{q})\|^2

この問題は、レーベンバーグ・マルカート法により解かれる。拘束関数のヤコビ行列

\mathbf{J}(\mathbf{q}) = \frac{\partial \mathbf{r}}{\partial \mathbf{q}}

を計算し、正規方程式（normal equations）

(\mathbf{J}^T \mathbf{J} + \lambda \mathbf{I}) \Delta\mathbf{q} = -\mathbf{J}^T \mathbf{r}

を反復的に解くことで、拘束を満たす機構の状態が求められる。

Sketchpadから現代へ

驚くべきことに、実は上記で解説したガウス・ニュートン法的な発想は1963年のSketchpadですでに実装されていた。Sutherland 自身は「ガウス・ニュートン法」という用語を使ってはいなかったが、現代の最適化理論のレンズを通して見ると、Sutherlandのシステムは、制約に対して局所ヤコビ行列 J_b = \partial \mathbf{g} / \partial x_b を用いた正規方程式 (J_b^T J_b) \Delta_b = -J_b^T \mathbf{g} をブロックごとに解いているものであり、その更新式はガウス・ニュートン法と形式的に一致する。さらに、ブロックごとに順番に更新を適用する点は、ガウス・ザイデル法（Gauss–Seidel method）的な反復戦略とも解釈できる。

60年後の現在、このガウス・ニュートン法的なアルゴリズムがCADシステムにも受け継がれている。オープンソースの3D CADソフトウェアFreeCAD[11]のSketcherモジュールでは、planegcsにおいて、制約の種類や構造に応じて複数の戦略（解析解、ブロック分解、反復法など）を組み合わせているが、非線形制約の反復解法としてレーベンバーグ・マルカート法を採用している部分が存在する。以下にその代表的な実装パターンを示す。

// FreeCAD Sketcher の Levenberg-Marquardt 実装の簡略版
for (iter = 0; iter < maxIter && !converged; ++iter) {
    // ヤコビ行列の計算
    subsys->calcJacobi(J);

    // ガウス・ニュートン近似：A = J^T * J, g = J^T * e
    A = J.transpose() * J;
    g = J.transpose() * e;

    // 減衰項を追加：A = A + μI はレーベンバーグ・マルカート法
    for (int i = 0; i < xsize; ++i) {
        A(i, i) += mu;
    }

    // 増強された正規方程式を解く：A*h = g
    h = A.fullPivLu().solve(g);

    // パラメータを更新：x_new = x + h
    x_new = x + h;

    // 誤差が減少したかチェックし、μを適応的に調整
    if (error_decreased) {
        mu *= 0.333;  // 減衰を弱めてガウス・ニュートン法に近づく
        x = x_new;
    } else {
        mu *= 2.0;    // 減衰を強めて最急降下法に近づく
    }
}

コード中の A = J.transpose() * J はガウス・ニュートン近似、A(i,i) += mu による減衰項の追加と mu の適応的調整は、本稿で解説したレーベンバーグ・マルカート法そのものだ。Sketchpadから現在のFreeCADまで、制約ベース設計のアルゴリズムは変わっていない。

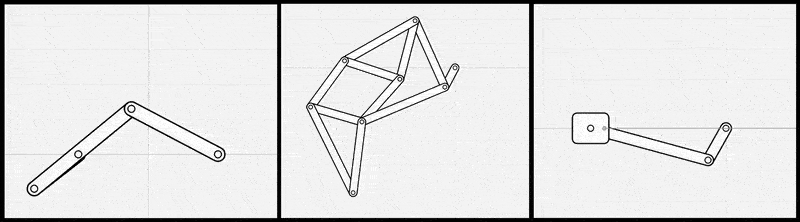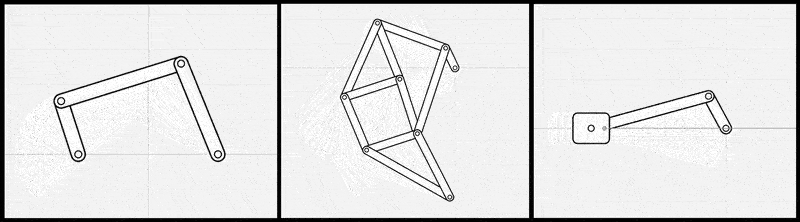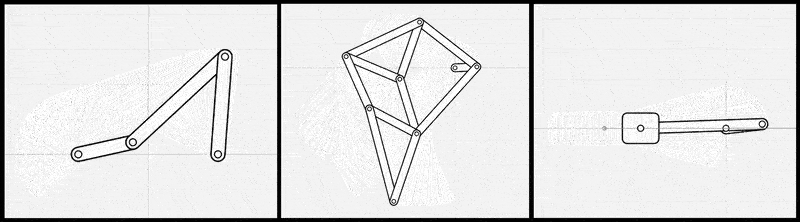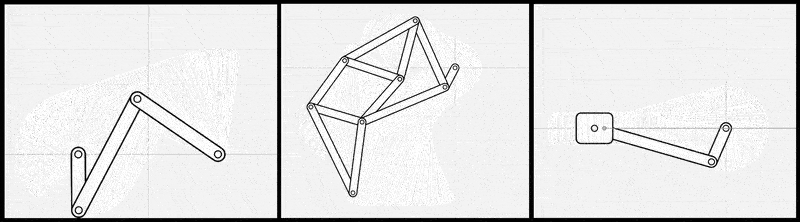
さらに、冒頭で触れたリンク機構設計ソフトMotionGenでも、リンク機構の順問題解析において同様にレーベンバーグ・マルカート法が採用されている[1]。MotionGenでは、ニュートン法の2つのバリエーション（ニュートン法とレーベンバーグ・マルカート法）を比較検討した結果、「ほとんどのシナリオでレーベンバーグ・マルカート法がニュートン法よりも高速に収束する傾向」が評価された。このように、この手法が制約充足問題の標準的な解法として確立されていることがわかる。

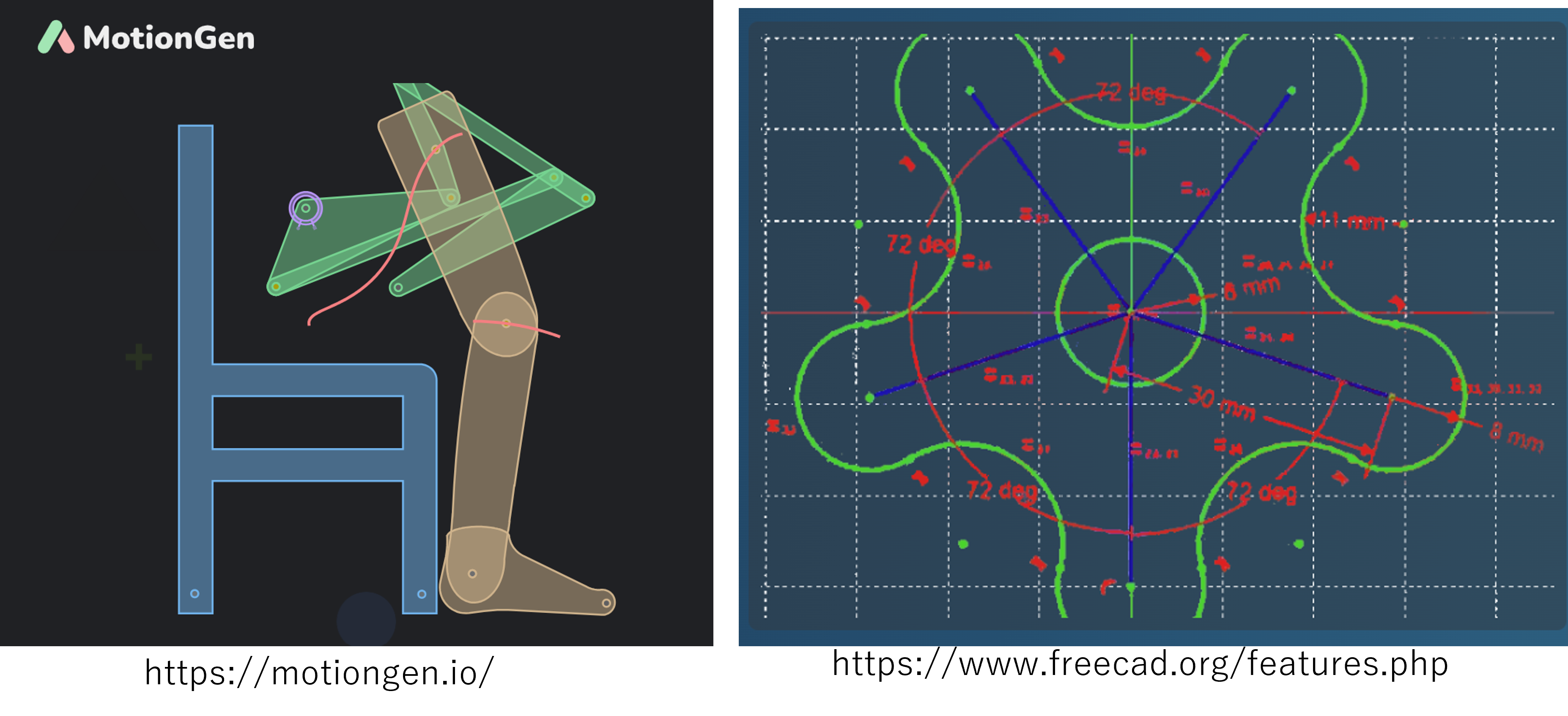
図8: 左 MotionGen、右 FreeCAD の 2D Sketcher

ケーススタディ

本章では、本稿で解説した手法を活用して、実際にブラウザ上でリンク機構を動かせるデモンストレーションを示す。読者はブラウザ上でリンク機構のパラメータをリアルタイムに変更し、拘束充足の挙動を体験できる。Sutherlandが述べた「5分で構築し、1時間遊ぶ」設計哲学を、技術で追体験する試みである。理論だけでなく、実際に触れることで、制約ベース設計の面白さが理解できるだろう。

レーベンバーグ・マルカート法の実装

ブラウザ上でのリンク機構の可視化の実装にはJavascriptのライブラリ p5.js[12]を用い、線形代数の計算にはml-matrix[13]を使用した。まずは第2章の数式

\mathbf{q}_{k+1} = \mathbf{q}_k - (\mathbf{J}_k^T \mathbf{J}_k + \lambda \mathbf{I})^{-1} \mathbf{J}_k^T \mathbf{r}_k

の実装部分を見てみよう。 hessianApprox = J^T * J によりヘッセ行列を \mathbf{J}^T \mathbf{J} で近似し、gradientVector = J^T * r により勾配 \nabla f = \mathbf{J}^T \mathbf{r} を計算する様子がわかる。

function levenbergMarquardtStep(jacobianMatrix, residualVector, lambda) {
    const jacobianTranspose = jacobianMatrix.transpose();
    const hessianApprox = jacobianTranspose.mmul(jacobianMatrix);
    const gradientVector = jacobianTranspose.mmul(residualVector);

    let stateIncrement;
    let currentLambda = lambda;
    const maxAttempts = 10;  // 無限ループ防止

    // Cholesky分解が成功するまでλを増やし続ける
    for (let attempt = 0; attempt < maxAttempts; attempt++) {
        const regularizedHessian = hessianApprox.clone();

        // J^T J + λI を構築
        for (let i = 0; i < regularizedHessian.rows; i++) {
            regularizedHessian.set(i, i, regularizedHessian.get(i, i) + currentLambda);
        }

        try {
            // Cholesky分解で (J^T J + λI) Δx = -J^T r を解く
            // 成功 → J^T J + λI が正定値
            stateIncrement = new CholeskyDecomposition(regularizedHessian).solve(gradientVector.clone().mul(-1));
            break;  // 成功したのでループ終了
        } catch {
            // Cholesky分解失敗 → J^T J + λI が正定値でない → λ不足
            currentLambda *= 10;  // λを10倍にして再試行

            if (attempt === maxAttempts - 1) {
                // 最終試行でも失敗した場合は、非常に大きなλで強制的に解く
                console.warn(`Cholesky分解が${maxAttempts}回の試行後も失敗しました。非常に大きなλを使用します。`);
                throw new Error("正定値行列を見つけられませんでした");
            }
        }
    }

    return { stateIncrement, lambda: currentLambda };
}

Cholesky分解の成否を正定値性の判定に利用している点に注目したい。厳密には、\lambda > 0 ならば \mathbf{J}^T \mathbf{J} + \lambda \mathbf{I} は数学的に正定値だが、浮動小数点演算の誤差により対称性がわずかに崩れたり、非常に小さな負の対角成分が生じたりすることがあり、その結果 Cholesky 分解が失敗することがある。本実装ではこれを実用的な障害として扱い、失敗時に自動的に \lambda を増やすことで数値的安定性を回復し、ロバストな動作を実現している。

なお、この \lambda の増加は緊急避難的な処理であり、Cholesky分解での調整は数値的な安定性を確保するための補助的な役割を担う。本稿の簡易版では、後述のゲイン比は用いず、単純な採否判定で \lambda を上下させる運用とする。

さらに、レーベンバーグ・マルカート法の1イテレーション全体を見てみよう。

function performSingleLMIteration(constraints) {
    const iterationStartTime = performance.now();
    let totalAssemblyTime = 0;

    // STEP 1: 現在の状態を評価
    const assemblyStartTime = performance.now();
    const { residualVector: currentResidualVector, jacobianMatrix: currentJacobianMatrix } = computeResidualAndJacobian(constraints);
    totalAssemblyTime += performance.now() - assemblyStartTime;

    const currentCost = COST_HALF * currentResidualVector.transpose().mmul(currentResidualVector).get(0, 0);

    // STEP 2: 探索方向の計算
    const { stateIncrement: searchDirection, lambda: usedLambda } = levenbergMarquardtStep(currentJacobianMatrix, currentResidualVector, lambda);
    lambda = usedLambda;

    // STEP 3: 試行更新を適用
    const initialLinksState = deepCopy(links);
    applyStateIncrement(searchDirection);

    // コストを評価
    const trialAssemblyStartTime = performance.now();
    const { residualVector: trialResidualVector } = computeResidualAndJacobian(constraints);
    totalAssemblyTime += performance.now() - trialAssemblyStartTime;

    const trialCost = COST_HALF * trialResidualVector.transpose().mmul(trialResidualVector).get(0, 0);

    // STEP 4: 簡易版の採否とλ調整
    if (trialCost < currentCost) {
        // 減少したら採用し、λを縮小（Gauss-Newton法に近づく）
        lambda = Math.max(lambda * LM_LAMBDA_DECAY, LM_LAMBDA_MIN);
    } else {
        // 減少しなければ棄却し、元に戻してλを拡大（最急降下法に近づく）
        for (let i = 0; i < links.length; i++) {
            Object.assign(links[i], initialLinksState[i]);
        }
        lambda = Math.min(lambda * LM_LAMBDA_GROW, LM_LAMBDA_MAX);
    }

    const iterationEndTime = performance.now();
    return {
        assemblyTime: totalAssemblyTime,
        totalTime: iterationEndTime - iterationStartTime
    };
}

現在の機構状態から残差ベクトル \mathbf{r} とヤコビ行列 \mathbf{J} を計算し、減衰正規方程式を解いて更新量 \Delta\mathbf{q} を得る。コスト f(\mathbf{q}) が減少すれば更新を採用し \lambda を縮小、増加すれば棄却し \lambda を拡大する。この簡単な戦略により、ガウス・ニュートン法と最急降下法の間を適応的に遷移する。

最後に、レーベンバーグ・マルカート法のイテレーションを複数回実行する関数を示す。実行回数は SOLVER_SUBSTEPS 回である。重要なのは、制約条件を1回構築し、複数イテレーションで再利用している点である。この設計により、制約構築のコストを分散し、計算効率を高めることができる。

function runSolverSubsteps() {
    const start = performance.now();
    let assemblyTimeTotal = 0;
    let coreTimeTotal = 0;

    // 現在の制約条件を構築（全イテレーションで共通）
    const constraints = buildConstraints();

    for (let i = 0; i < SOLVER_SUBSTEPS; i++) {
        const { assemblyTime, totalTime } = performSingleLMIteration(constraints);
        assemblyTimeTotal += assemblyTime;
        coreTimeTotal += (totalTime - assemblyTime);
    }

    profilingMetrics.lastSolverMilliseconds = performance.now() - start;
    profilingMetrics.lastSolverAssemblyMilliseconds = assemblyTimeTotal;
    profilingMetrics.lastSolverCoreMilliseconds = coreTimeTotal;
}

残差ベクトルとヤコビ行列の構築

さらに、ジョイントの残差とヤコビアンがどのように実装されているのか、実際のコードを参考に見ていこう。

回転ジョイントは、第3.2.1節で定式化した拘束条件の中核である。以下にその実装を示す。このコードは、定式化した拘束条件を直接実装している。

function computeWorldPoint(link, localPos) { // R*q + p
    const rotationMatrix = rotationMatrixFromDegrees(link.angleDeg);
    const translationVector = toCol(link.pos[0], link.pos<a href="#ref-1">[1]</a>);
    return rotationMatrix.mmul(toCol(localPos[0], localPos<a href="#ref-1">[1]</a>)).add(translationVector); // [2x1]
}

// ∂(R*q + p)/∂[px, py, angleDeg] = [ I2 | RΩq * (π/180) ]
function computeJacobianBlock(link, localPos) {
    const rotationMatrix = rotationMatrixFromDegrees(link.angleDeg);
    const localPointVector = toCol(localPos[0], localPos<a href="#ref-1">[1]</a>);
    const angleDerivative = rotationMatrix.mmul(Omega).mmul(localPointVector).mul(DEG2RAD); // [2x1]
    const jacobianBlock = new Matrix([
        [1, 0, angleDerivative.get(0, 0)],
        [0, 1, angleDerivative.get(1, 0)],
    ]); // [2x3]
    return jacobianBlock;
}

function computeRevoluteJointResidual(linkA, linkB, localPosA, localPosB) {
    const jointPointOnLinkA = computeWorldPoint(linkA, localPosA);
    const jointPointOnLinkB = computeWorldPoint(linkB, localPosB);
    return jointPointOnLinkA.sub(jointPointOnLinkB); // [2x1]
}

function computeRevoluteJointJacobianBlocks(linkA, linkB, localPosA, localPosB) {
    const jacobianBlockA = linkA.fixed ? null : computeJacobianBlock(linkA, localPosA);
    const jacobianBlockB = linkB.fixed ? null : computeJacobianBlock(linkB, localPosB).mul(-1);
    return { jacA: jacobianBlockA, jacB: jacobianBlockB };
}

また、リンク機構を駆動するアクチュエータ（モーター）も、拘束条件として表現できる。アクチュエータ制約は、2つのリンク間の相対角度 \varphi_B - \varphi_A を目標値 \varphi_{\text{target}} に保つ拘束である。実装は以下の通りである：

function computeRelativeAngle(linkA, linkB) {
    return linkB.angleDeg - linkA.angleDeg;
}

function normalizeAngleDiff(angle) {
    let normalized = angle;
    while (normalized > 180) normalized -= 360;
    while (normalized < -180) normalized += 360;
    return normalized;
}

function computeActuatorResidual(linkA, linkB, targetRelativeAngleDeg) {
    const currentRelativeAngle = computeRelativeAngle(linkA, linkB);
    // 残差は -180 ~ +180 の範囲に正規化（最短経路で目標角度に到達）
    return normalizeAngleDiff(currentRelativeAngle - targetRelativeAngleDeg);
}

function computeActuatorJacobianBlocks(linkA, linkB) {
    // ヤコビアン: ∂(residualAngle)/∂state = ∂(angleB - angleA)/∂state
    // residualAngle = angleB - angleA - target なので：
    // - linkA の angleDeg に対して: -1 （linkA が回転すると残差が減少）
    // - linkB の angleDeg に対して: +1 （linkB が回転すると残差が増加）
    // - 位置 (px, py) に対して: 0 （相対角度なので位置は無関係）
    const jacA = linkA.fixed ? null : -1;  // ∂/∂angleA = -1
    const jacB = linkB.fixed ? null : 1;   // ∂/∂angleB = +1
    return { jacA, jacB };
}

ヤコビアン：相対角度は線形なので、ヤコビアンは単純である。linkAに対して -1、linkBに対して +1、位置に対して 。位置と角度が非線形結合する回転ジョイントとは対照的である。

さらに、マウスドラッグも拘束として扱う。ユーザーがリンクを掴むと、そのローカル座標上の点をマウス位置に固定する拘束が追加される。ドラッグ中はアクチュエータを無効化し、手動操作を優先させる。

function buildConstraints() {
    // ドラッグ制約: マウスでリンクをドラッグ中の場合、そのリンクの特定点を
    // マウス位置に固定する制約を生成
    const drag = dragging ? {
        linkID: dragging.linkID,      // ドラッグ中のリンクID
        local: dragging.local,         // リンクのローカル座標系で掴んでいる点
        target: [mouseWorld.x, mouseWorld.y]  // ワールド座標系での目標位置
    } : null;

    // アクチュエータ制約: 各関節の相対角度を目標値に固定する制約
    // ドラッグ中はアクチュエータを無効化（手動操作を優先）
    const actuators = dragging ? [] : actuatorStates.map(state => ({
        jointID: state.jointID,                           // 制約する関節のID
        targetRelativeAngleDeg: state.targetRelativeAngleDeg  // 目標相対角度（度）
    }));

    return { drag, actuators };
}

以上の実装により、毎フレーム、現在の制約を構築し、ソルバーを数回イテレーションさせ、収束した状態を描画できる。この単純な繰り返しが、拘束を満たしながらユーザー操作にリアルタイムで応答する機構シミュレーションを実現できる。

リンク機構の例

4節リンク機構

4節リンク機構は、Sutherlandが3つの拘束で遊んでいたものと同様の基本的な機構である。底面にあたるリンクはStatic状態として固定し移動しない。

テオ・ヤンセン機構の概要

テオ・ヤンセン機構 Theo Jansen Mechanism は、オランダの芸術家テオ・ヤンセンが設計した歩行機構である。11本のリンク、13個のジョイント、閉ループを形成する構造を持ちながら、単一のクランクの回転のみで滑らかな歩行動作を実現する。

拡張性・スライダージョイント

汎用的定式化では、新しい拘束タイプを容易に追加できる。例として、ピストンやスライド機構に用いられるスライダージョイント (Sliding Joint) を示す。ピンがスロット（溝）に沿って直線的に移動できる拘束である。

スライダージョイントは「ピン位置 \mathbf{x} _j がスロット直線上にある」拘束である。スロットの両端点を \mathbf{x} _{i1}, \mathbf{x} _{i2} とすると、外積で以下のように表現できる：

C = (\mathbf{x}_j - \mathbf{x}_{i1}) \times (\mathbf{x}_j - \mathbf{x}_{i2}) = 0

2次元では外積のZ成分のみが非ゼロとなりスカラー拘束となる。スロット長さで正規化することで、残差が他の拘束と同じ距離次元で扱える。

まとめ

今回はIvan Sutherlandが1963年のSketchpadで示した「5分で構築し、1時間遊べる」設計哲学を、連続最適化生かしたインタラクティブなリンク機構の実装を通じて味わうことである。制約充足の数学的枠組みが、設計者の意図を制約条件として直接的に表現し、システムがそれをリアルタイムに解釈・実行することで、「試行錯誤による発見」の意味を感じられたのではないだろうか。

この仕組みは、リンク機構に限らず、CADソフトウェアの幾何学的制約、ロボットアームの運動学など、広範な制約充足問題に適用できる。実際、1963年のSketchpadから現在のFreeCAD、そしてNatureArchitects社のCraneへと、60年にわたって共通のアルゴリズムが使われている。

ここから先、次の挑戦として立ちはだかるのが「所望の軌跡を描くリンク機構を自動的に設計する」といった逆問題になる。逆問題においては、順問題の制約充足を維持しながら、設計目的を最小化するようにパラメータを最適化する、二段階にまたがった最適化問題として定式化できる。本稿で構築した順問題の数学的基盤は、この逆問題を解くための足場となる。

次の機会には、Sutherlandが夢見たインタラクティブな設計哲学を、逆問題という次元へと拡張し、Computational Mechanism Designの世界を旅していきたい。

---

参考文献

[1] Lyu, Z., Purwar, A., and Liao, W., "A Unified Real-Time Motion Generation Algorithm for Approximate Position Analysis of Planar N-Bar Mechanisms," ASME Journal of Mechanical Design, vol. 146, no. 6, p. 063302, 2024.
DOI: https://doi.org/10.1115/1.4064132

[2] Kai Suto, Yuta Noma, Kotaro Tanimichi, Koya Narumi, Tomohiro Tachi, "Crane: An Integrated Computational Design Platform for Functional, Foldable, and Fabricable Origami Products," ACM Transactions on Computer-Human Interaction, vol. 30, no. 4, Article 52, 2023.
DOI: https://doi.org/10.1145/3576856
オンライン版：https://dl.acm.org/doi/10.1145/3576856

[3] Sutherland, I. E., "Sketchpad: A Man-Machine Graphical Communication System," PhD Thesis, Massachusetts Institute of Technology, 1963.
オンライン版：https://www.cl.cam.ac.uk/techreports/UCAM-CL-TR-574.pdf

[4] Nocedal, J., and Wright, S., Numerical Optimization, 2nd ed., Springer, 2006.
ISBN: 978-0-387-30303-1

[5] 金森敬文・鈴木大慈・竹内一郎・佐藤一誠『機械学習のための連続最適化』講談社, 2016.
ISBN: 978-4-06-152904-9

[6] Hesse, L. O., "Über die Criterien des Maximums und Minimums der einfachen Integrale," Journal für die reine und angewandte Mathematik (Crelle's Journal), vol. 54, pp. 227-273, 1857.
オンライン版：https://gdz.sub.uni-goettingen.de/id/PPN243919689_0054

[7] Jacobi, C. G. J., "De determinantibus functionalibus," Journal für die reine und angewandte Mathematik (Crelle's Journal), vol. 22, pp. 319-359, 1841.
オンライン版：https://gdz.sub.uni-goettingen.de/id/PPN243919689_0022

[8] Gauss, C. F., Theoria motus corporum coelestium in sectionibus conicis solem ambientium, Hamburg: Sumtibus F. Perthes et I. H. Besser, 1809.
オンライン版（英訳）：https://archive.org/details/bub_gb_ORUOAAAAQAAJ

[9] Levenberg, K., "A Method for the Solution of Certain Non-Linear Problems in Least Squares," Quarterly of Applied Mathematics, vol. 2, no. 2, pp. 164-168, 1944.
JSTOR: https://www.jstor.org/stable/43633451

[10] Marquardt, D. W., "An Algorithm for Least-Squares Estimation of Nonlinear Parameters," Journal of the Society for Industrial and Applied Mathematics, vol. 11, no. 2, pp. 431-441, 1963.
DOI: https://doi.org/10.1137/0111030

[11] FreeCAD Development Team, "Sketcher Workbench - planegcs Geometric Constraint Solver," FreeCAD GitHub Repository.
ソースコード：https://github.com/FreeCAD/FreeCAD/blob/main/src/Mod/Sketcher/App/planegcs/GCS.cpp
最終アクセス：2025年

[12] Casey Reas and Lauren McCarthy, "p5.js," https://p5js.org/, 最終アクセス：2025年

[13] Michaël Zasso et al., "ml-matrix: Machine learning tools in JavaScript," https://github.com/mljs/matrix, 最終アクセス：2025年

---