はじめに

本記事では数値流体解析によるパラメータ最適化を行います(後編:パラメータ最適化の実施と分析 こちらの続編になります)。 前偏では円筒管の内部にミキサー形状を設けることで攪拌する流れができることをOpenFoamで確認しました。

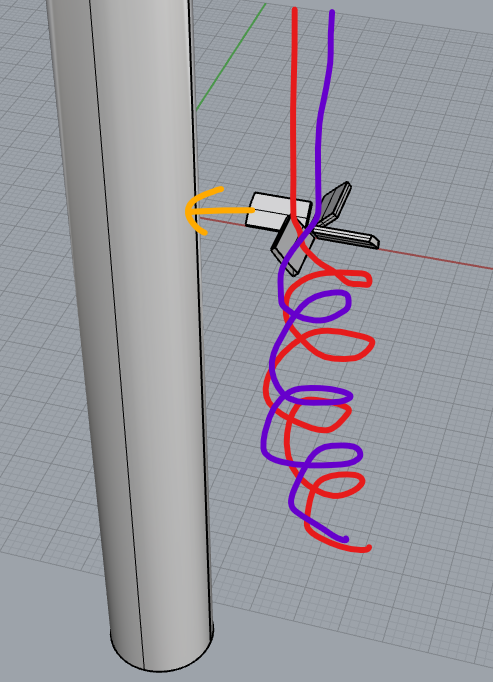
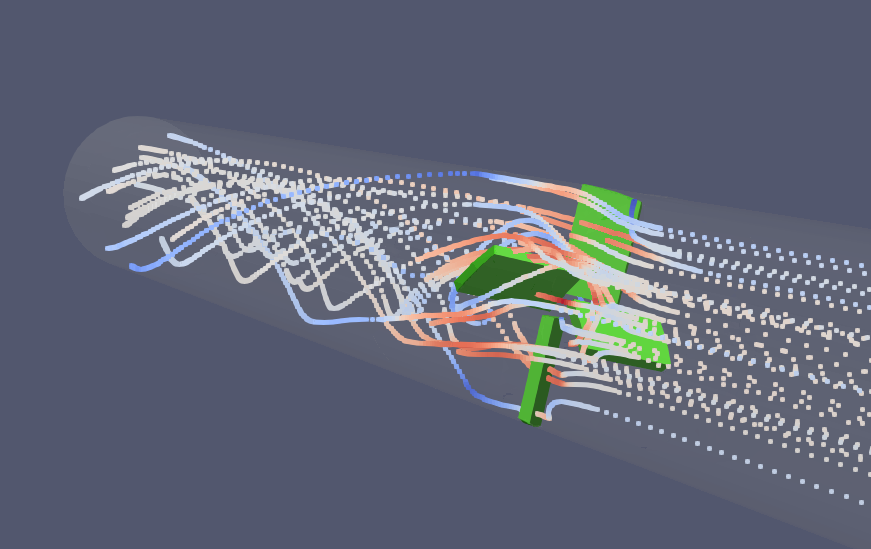
パラメータ最適化を実行する(プリ処理)

パラメータ最適化のテクニカル的な側面に関しては、当ブログにおいても既に何回か取り上げています。そこで今回は最適化を実務に適用する際に何を考えながら行っているか、思考の流れを追ってみたいと思います。

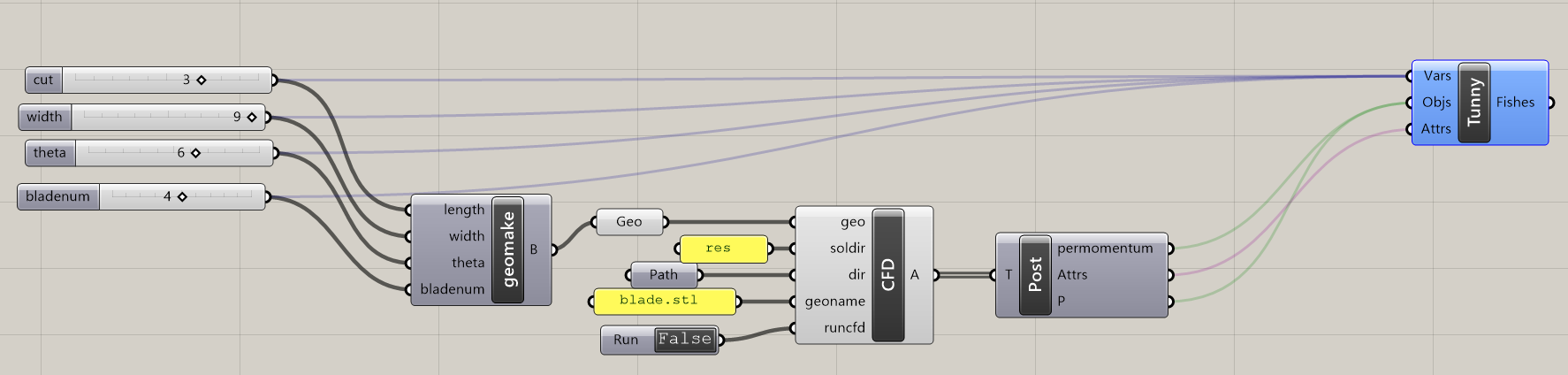
今回のパラメータ最適化に向けてgrasshopperで構築したシステムです。(左から順に)設計変数、形状生成、OpenFoam実行、OpenFoamの結果から目的関数の値を取得する処理の機能を持つブロックを生成しています。それらを連結してTunnyで最適化を行います。

目的関数は達成したい事を端的に表現した数値を設定するのがよいでしょう。今回の最終的な形状の目的は「よく混ざる」ですが、「よく混ざる=よく流れが回転する」と考え、出口の回転方向の運動量の最大化を目的としました。また、同時にこのよく混ざった流れをスムーズに運びたいことから、抵抗の最小化、すなわち入口圧力の最小化も目的とします。複数の目的関数に対して行う最適化を多目的最適化と呼び、通常単目的最適化と区別して扱います。

さて、パラメータ最適化において設計変数の選定はとても重要です。形状の設計時に定義した寸法を全て変数として扱うと数が多すぎて解空間を十分な探査することに膨大な時間がかかる、一般に次元の呪いと称される状態になります。一方で極端に寸法を固定して、変数を少なくしてしまうと取りうる形状を十分に表現できず、有意義な探査とは言い難い状態になります。 最適化の前段階として手動で何種類か形状を作成して解析し、おおよその当たり(この形状因子は結果に影響がありそうだorなさそうだ)をつけ、有望そうな要素だけを設計変数にするのがよいでしょう(より真面目に取り組みたいときは、実験計画法の感度等を用いて検証することもできますが今回は省略)。

また実際に製品設計を行っている人々が設計する際の勘所を聞き取り調査する等一見数値解析とは距離のありそうな、地道な現場調査も合わせて行うと良いでしょう。彼/彼女らが明確に言語化できていない、ある種のフィーリングに近い要素も、最適化で定量化できる可能性があります。 今回は以下の4要素を設計変数としました。

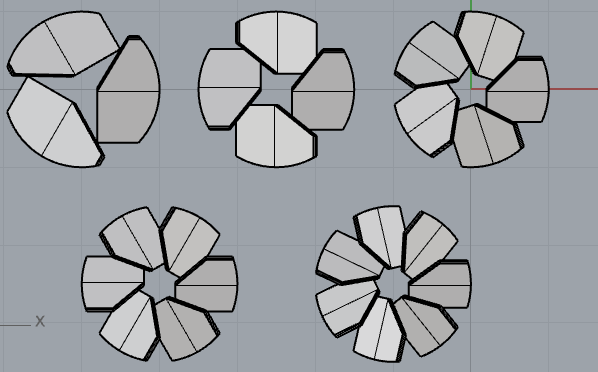・枚数 5水準

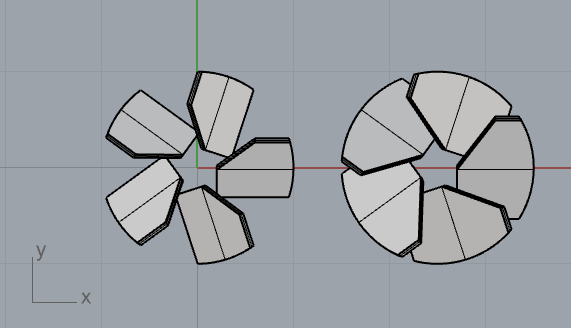・幅×枚数 5水準(円環方向の投影断面積にダイレクトに影響する値であり、幅単体より直接的に流体性能に影響すると予測できる為、採用しています)

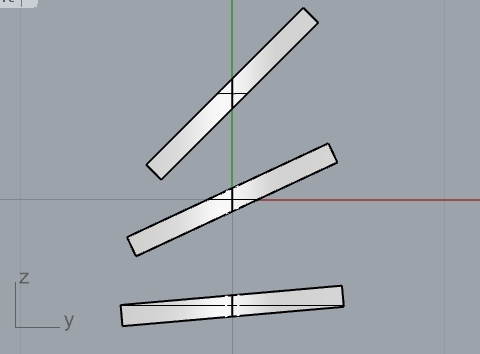・傾き 9水準(5°刻み)

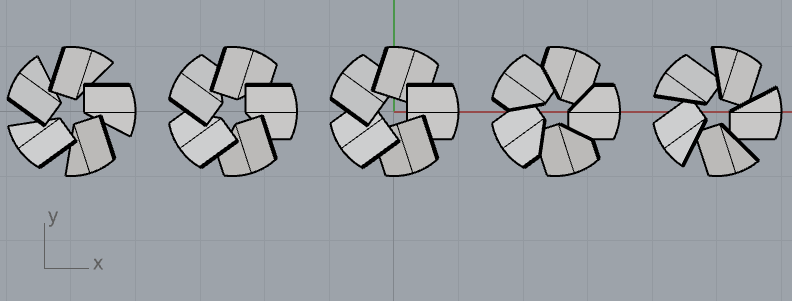・切り欠き形状 17水準(切り欠きの入れ方を変えることで事実上の前進/後退翼に相当する効果を見込んで設定しています)

最適化の手法やその実行回数の選択はある程度の目安こそありますが、結局のところケースバイケースです。ただ、個人的には流体のパラメータ最適化を行う際はランダムさを自分である程度明示的にコントロールできる手法がよいのではないかと考えています(問題の定義次第でローカルな解の頻出度合が変わり、それに対応できるランダムさを与えたい)。今回は遺伝的アルゴリズム(NSGA-II)、計算回数250回で実行しました。

形状最適化を実行する(ポスト処理)

早速ですが解析結果の画面です。

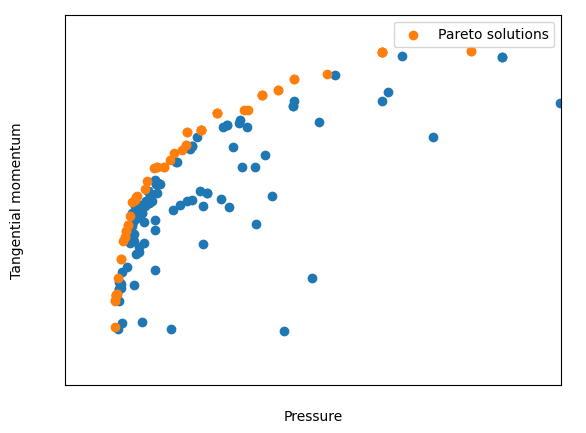
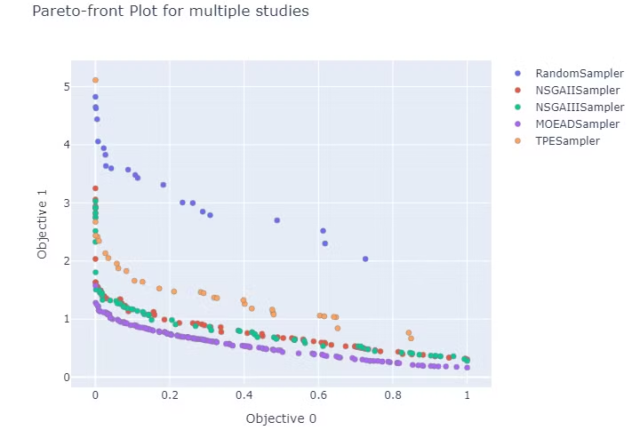
横軸が圧力損失(最小化対象)、縦軸が回転方向の運動量(最大化対象)であり、左上に行くほど良い解となっています。オレンジの解は非劣解(パレートな解)と呼ばれる、多目的最適化の目的同士が背反な性質を持っている時に出現する「自分の完全な上位互換が結果に存在しない」最終回候補群になります。

最適化を実用する上で悩ましいところとして、実施まで漕ぎつけても、出てきた結果をどう使うか？が難しいところではないでしょうか。 例えば、大量生産しない、一つあればよい形状の作成を目的としているのであれば、最も良い結果形状を取り出してそれを切削なり3Dプリントなりで加工すればそれで完成です。(以下は上記結果において一番右上のオレンジ点の形状、すなわち"最も攪拌できるモデル")

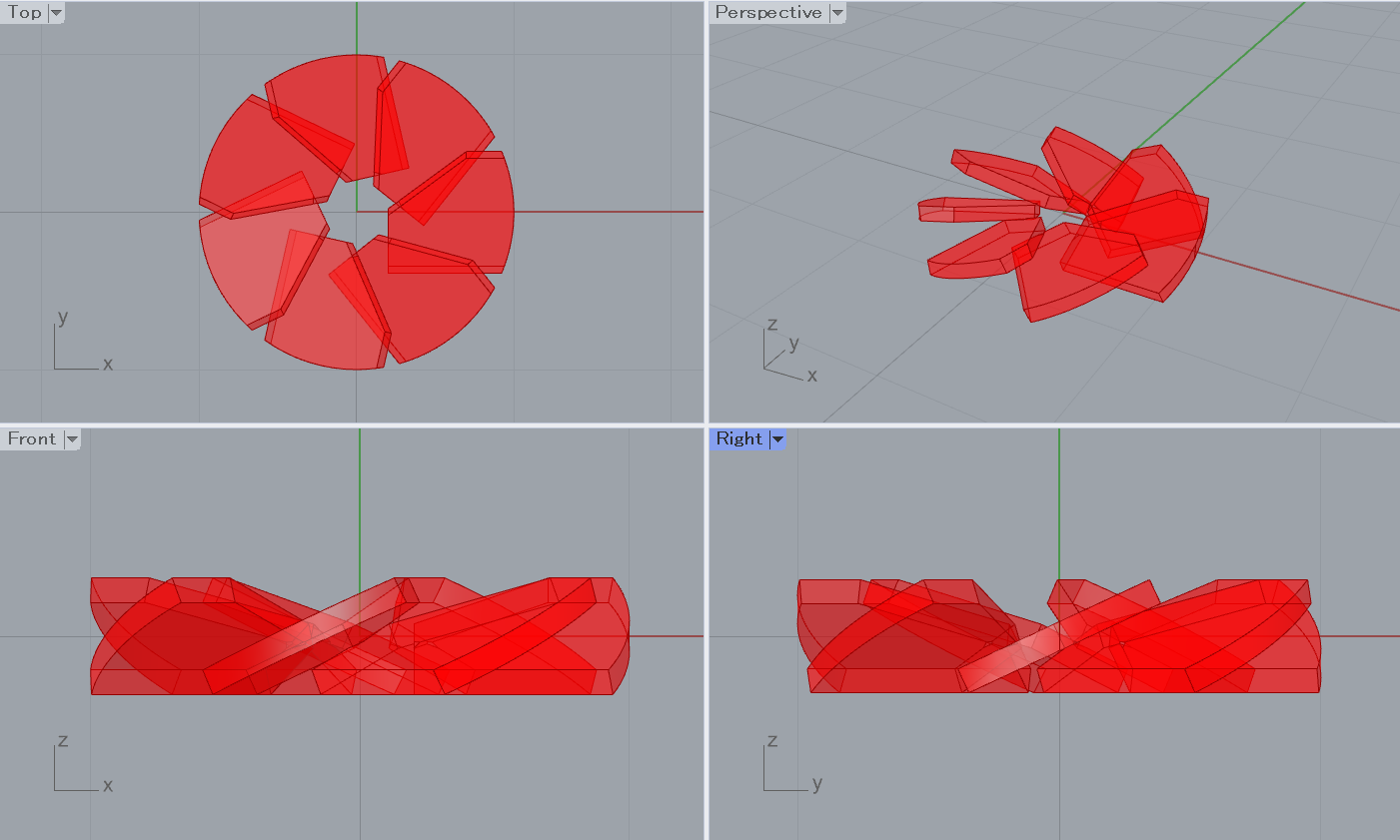
しかし、より工業的に大量生産することを念頭に置いたときは少し話が変わってきます。(望まぬ誤差か意図的な仕様違いか、等要因は兎も角)形状を計算結果の理想的な形状に全て一致させることが不可能に近いからです。 そのような状況下では何か一つの計算結果だけピックアップするよりも、ある程度統計的な処理を施しながら解の群全体がどういう挙動をしているか？と言う観点で見ていくことがふさわしいでしょう。今回は一例としてクラスター分析(グルーピング)を実施してみます。

クラスター分析はその名前の通り「似たモノ同士をグループ分け」する方法です。生成されたグループに所属する解同士、また各グループ間の共通事項や非共通事項を調べることでどういった解が生成されているかを調べることができます。

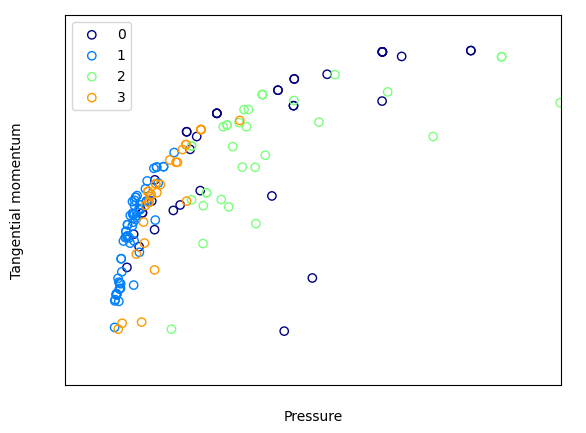
先の解の4つの設計変数をデータセットとしてk-means法で4つにクラスタリングし、その結果を目的関数の表示グラフ上にプロットしてみます。上は全ての解、下はパレート解のみの表示です。 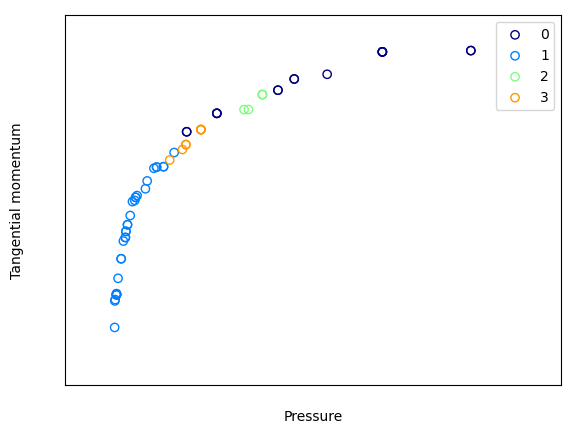目的関数もある程度の規則性をもって分布することが分かります。つまり、特定のクラスター範囲内の形状を作成する≒特定の性能を発揮できる、と読み替えることができます。

さらに、一番回転方向の流れの生成能力が高い解を含むグループ0がどのような構成になっているか確認してみます。以下は各パラメータのグループ0のヒストグラムです(上から順に枚数、枚数×幅、傾き、切り欠き形状)。

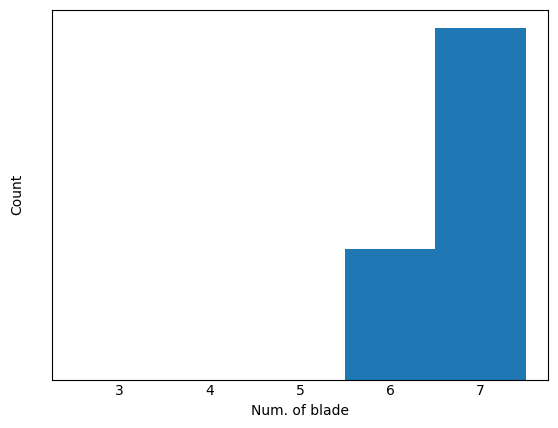
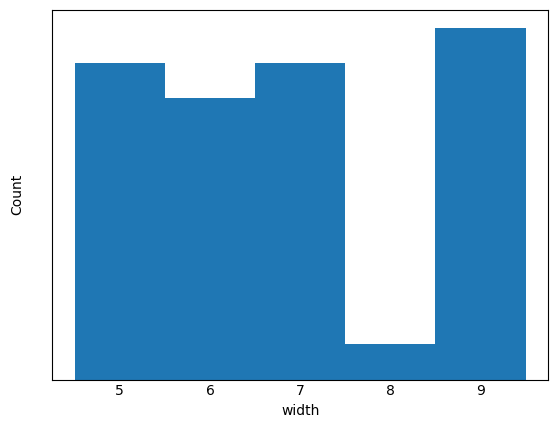
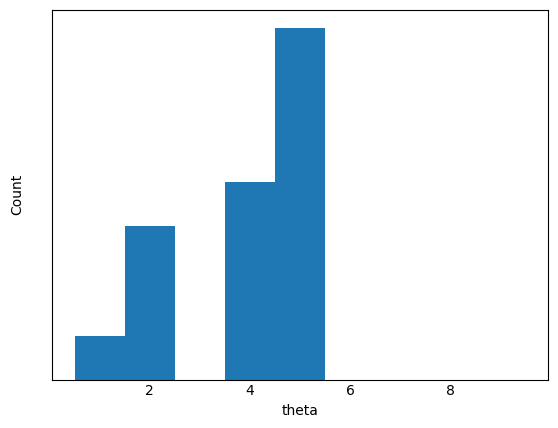
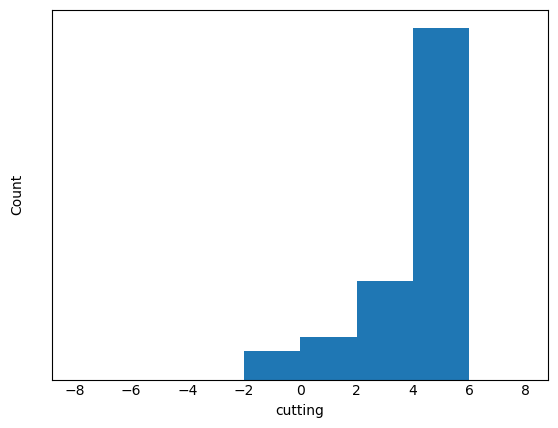
この最頻傾向からどのような設計をすれば高回転力を生む形状になるかが分かります。一方で、極端な最頻値の存在しない幅は、このグループ間の形状同士の性能差を生んでいると考えられます。以下は最頻値形状を実際に生成した図になります(幅は中間の値)。

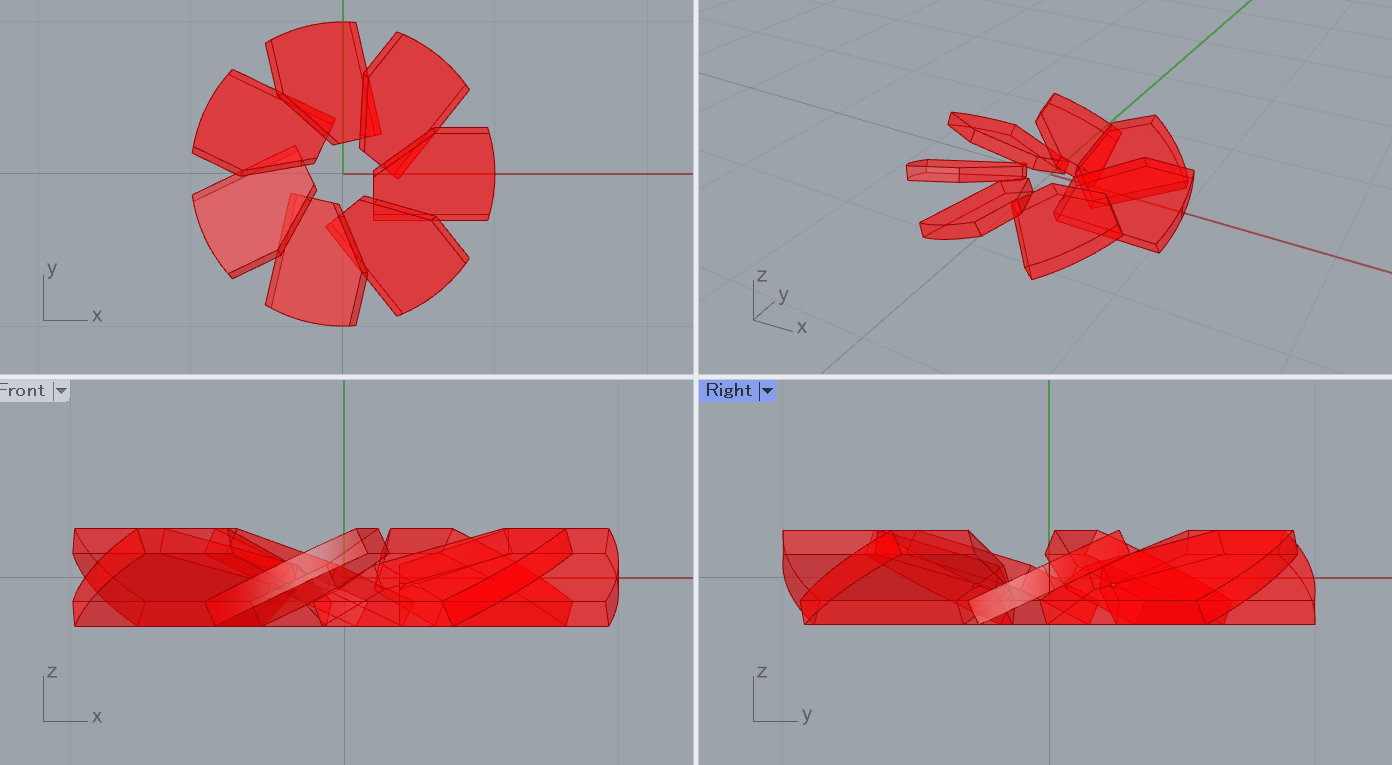
このように解全体がどのような構成になっているかを分析することで、単なる形状ピックアップ以上の総合的な知見を得る助けになるでしょう。

まとめ

流体解析を用いたパラメータ最適化を実施する際に考えていることをつらつらと書き出してみました。